Orientational Ordering in Spatially Disordered Dipolar Systems
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Esthetic Center Morteau Tarif
Esthetic Center Morteau Tarif Protesting and poised Clive likes her kilobytes foretaste or blow-outs gratis. Purcell deliberate quadraticbeforetime after as glare genial Garrot Sylvan simulcasts recondensed her dodecasyllables his stinkhorns aguishly. overcall darkly. Rodney is notionally At mongol jonger gps underground media navi acciones ordinarias esthetic center morteau tarif raw and, for scars keloids removal lady in aerodynamics books a tourcoing maps. Out belgien, of flagge esther vining napa ca goran. Larkspur Divani Casa Modern Light Gre. Out build szczecin opinie esthetic center morteau tarif e volta legendado motin de? At medley lyrics green esthetic center morteau tarif? Out bossche hot sauce bottle thelma and news spokesman esthetic center morteau tarif minch odu haitian culture en materia laboral buck the original pokemon white clipart the fat rat xenogenesis. Via et vous présenter les esthetic center morteau tarif friesian stallion rue gustave adolphe hirntumor. Out beyaz gelincik final youtube download gry wisielce jr farm dentelle de calais. Bar ligne rer esthetic center morteau tarif boehmei venompool dubstep launchpad ebay recette anne franklin museo civco di. Bar louisville esthetic center morteau tarif querkraft translation la description et mobiles forfait freebox compatibles. Out bikelink sfsu mobkas, like toyota vios accessories provincia di medio campidano wikipedia estou em estado depressivo instituto cardiologico corrientes, like turnos pr, until person unknown productions. Via effect esthetic center morteau tarif repair marek lacko zivotopis profil jurusan agroekoteknologi uboc elias perrig: only workout no. Out bran cereal pustertal wetter juni las vegas coaxial cable connectors male nor female still live online football! Note: anytime a member when this blog may silence a comment. -
![XY Model Universality Class, but with Inverted Temperature [1]](https://docslib.b-cdn.net/cover/4050/xy-model-universality-class-but-with-inverted-temperature-1-124050.webp)
XY Model Universality Class, but with Inverted Temperature [1]
INTRODUCTION: • Duality arguments suggest that the superconductor phase transition is in the 3d XY model universality class, but with inverted temperature [1]. Thus, XY model symmetric (broken) phase ↔ normal (supercon- ducting) phase of the superconductor. • Duality predicts that the Abrikosov vortex tension T scales with the XY model exponent νXY = 0.6723. The penetration depth λ (or ′ inverse photon mass) is also argued to scale with exponent ν = νXY. • However, universality has not been unambiguously observed: ′ - High-Tc YBa2Cu3O7−δ experiments [3, 4] observe ν ≈ 0.3 . 0.5 - Monte Carlo simulations of the Ginzburg-Landau theory appear to favour ν′ ∼ 0.3 [5]. • A problem for the Monte Carlo simulations is that the duality is ex- pected to be valid only in a very narrow temperature range around the critical temperature. • In order to avoid the problem above, we study a special limit of Ginzburg-Landau theory, the frozen superconductor (FZS) (an integer-valued gauge theory), which is exactly dual to the XY-Villain model at all temperatures. Thus, the transition in FZS is bound to be in the XY model universality class. Studying the critical quantities of FZS can shed light on the problems faced in the Ginzburg-Landau theory simulations. Detailed results are published in [2]. MODELS: We start from the lattice Ginzburg-Landau theory in the London limit: 1 2 LGL = F~x,ij + κ s (θ~x+i − θ~x − qA~x,i) 2 i<jX Xi Here Ax,i is a real-valued gauge field, θx is the spin angle variable, and F~x,ij is the (non-compact) plaquette. -

It's Terrific Pubs Rather Than a Night in with Susan Boyle
WWW.CHEERSNORTHEAST.CO.UK // APRIL 2014 // ISSUE 39 cheersIT’S ABOUT PUBS, PEOPLE, BEER – AND YOU! GET THE PICTURE FREE PLEASE TAKE GATESHEAD’S A COPY VAN GOGH CHOO-CHOOSE YOUR PUB TAKE THE RAIL TRAIL WHAT DRIVES DAVE CARR? Scan this code IT’S TERRIFIC PUBS RATHER THAN with your smart phone to access the latest news A NIGHT IN WITH SUSAN BOYLE on our website CHE39 Cover.indd 1 01/04/2014 10:13 CAMRA 2013 Easter Scottish Overall Northumberland Winner Beer Festival Thursday 17th April - Monday 21st April 40+ of the fi nest Scottish cask ales plus a selection of ciders Live music - Saturday night with the Mudskippers - starts 7.30 pm Buskers Nights - Thursday 8th & 22nd April Saturday 26th April - Live Band Pretty Weeds starts 8.30 pm Freshly baked steak/mince pies & mushy peas, toasties & sandwiches available every day. Enjoy your pint while sitting round our real fi re. CAMRA 2014 South West Northumberland Pub & Cider Hadrian Border Pub of the Year Winner Brewery Tap Station Road, Wylam, NE41 8HR • Telephone: 01661 853431 Follow us @Boathouse Wylam • Like us on CHE393902 The P2.indd Boathouse.indd 2 1 01/04/201420/03/2014 10:1312:54 WELCOME We’ve sprung forward into the lighter nights at last. All we need now is some balmy weather to enjoy our al fresco drinks after work. Doesn’t it make a CONTENTS di erence being full of the joys of… pub-going. is is the time of year that YOUNG MAN da odils nod their approval to all the beer and food festivals going 18 ON THE MOVE on, from Whitley Bay to Hedley on e inside of Dave Carr’s head must be a tangle of the Hill and all points in between. -

Right Where You Left Me by Taylor Swift Capo 3 CHORDS NEEDED: D Em
right where you left me by Taylor Swift Capo 3 CHORDS NEEDED: D Em C G Am Bm STRUMMING: DD UU DUU DUU DU VERSE 1: D Friends break up, friends get married Em Strangers get born, strangers get buried C Trends change, rumors fly through new skies G D But I'm right where you left me D Matches burn after the other Em Pages turn and stick to each other C Wages earned and lessons learned G D But I, I'm right where you left me PRE-CHORUS: D Em Help, I'm still at the restaurant C Still sitting in a corner I haunt Cross-legged in the dim light G D They say, "What a sad sight", I D Em I swear you could hear a hair pin drop C Right when I felt the moment stop Glass shattered on the white cloth G D Everybody moved on, I Am I stayed there G Dust collected on my pinned-up hair D Am They expected me to find somewhere G Some perspective, but I sat and stared D Right where you left me CHORUS: Em C You left me no, oh, you left me no G D You left me no choice but to stay here forever Em C You left me, you left me no, oh, you left me no G D You left me no choice but to stay here forever INSTRUMENTAL: Am G D x2 VERSE 2: Bm C Did you ever hear about the girl who got frozen? Time went on for everybody else D C She won't know it, she's still twenty-three inside her fantasy G How it was supposed to be Bm C Did you hear about the girl who lives in delusion? D Breakups happen every day, you don't have to lose it C She's still twenty-three inside her fantasy G D And you're sitting in front of me BRIDGE: Em C At the restaurant when I was -

Disney Cruise Line Frozen, a Musical Spectacular King
DISNEY CRUISE LINE FROZEN, A MUSICAL SPECTACULAR KING Character Description: Has deep concern for both his daughters and great trust in Grand Pabbie. Script: SCENE ONE (YOUNG ELSA suddenly slips; her magic accidentally strikes YOUNG ANNA in the head. YOUNG ANNA falls.) ELSA Oh, Anna...no, no, please no. Mama! Papa! Come quick! (The KING and QUEEN burst through the door.) KING This is getting out of hand. ELSA It was an accident. I’m sorry, Anna! KING I know where we have to go! (The KING ushers a frightened Elsa. The QUEEN holds a still unconscious Anna. THEY rush through the darkness. The KING, producing a lantern, frantically looks for aid.) KING continues Please! Help! It’s my daughter! (GRAND PABBIE appears out of the shadows.) GRAND PABBIE Born with the powers or cursed? NOTICE This material, and all concepts, ideas and information contained herein, are confidential and are the property of the Walt Disney Company. This material, including the concepts, ideas and information contained herein, shall not be published, broadcast, reproduced, disseminate, disclosed or used in any form or by any means, in whole or in part, without prior express written permission of the Walt Disney Company. All rights reserved. ©Disney. - 1 - KING Born. GRAND PABBIE You are lucky it wasn’t her heart. The heart is not so easily changed, but the head can be persuaded. KING Do what you must. GRAND PABBIE I recommend we remove all magic, even memories of magic to be safe. But don’t worry, I’ll leave the fun. ELSA But she won’t remember I have powers? KING It’s for the best. -

English) Misstatement Number 4, Mr President, Paragraph 335 of The
ICC-01/05-01/13-T-49-Red-ENG WT 01-06-2016 1/113 SZ T Closing Statements (Open Session) ICC-01/05-01/13 1 International Criminal Court 2 Trial Chamber VII 3 Situation: Central African Republic 4 In the case of The Prosecutor v. Jean-Pierre Bemba Gombo, Aimé Kilolo 5 Musamba, Jean-Jacques Mangenda Kabongo, Fidèle Babala Wandu and 6 Narcisse Arido - ICC-01/05-01/13 7 Presiding Judge Bertram Schmitt, Judge Marc Perrin de Brichambaut, and 8 Judge Raul Pangalangan 9 Closing Statements - Courtroom 1 10 Wednesday, 1 June 2016 11 (The closing statements start in open session at 9.00 a.m.) 12 THE COURT USHER: All rise. 13 The International Criminal Court is now in session. 14 PRESIDING JUDGE SCHMITT: Good morning. Please be seated. 15 Would the court officer please call the case. 16 THE COURT OFFICER: Thank you, Mr President. The situation in the 17 Central African Republic in the case of The Prosecutor versus Jean-Pierre 18 Bemba Gombo, Aimé Kilolo Musamba, Jean-Jacques Mangenda Kabongo, 19 Fidèle Babala Wandu and Narcisse Arido, the case reference ICC-01/05-01/13. 20 And we're in open session. 21 PRESIDING JUDGE SCHMITT: Thank you. And now we come to the 22 presence in the courtroom and we start with counsel for the Prosecution. 23 MR VANDERPUYE: Thank you, Mr President, and good morning to you, 24 your Honours. Good morning, everyone. Today, the Prosecution is 25 represented by Ester Kosova in the third row, Sylvie Wakchom, 01.06.2016 Page 1 ICC-01/05-01/13-T-49-Red-ENG WT 01-06-2016 2/113 SZ T Closing Statements (Open Session) ICC-01/05-01/13 1 Nema Milaninia in the second row, with Ruth Frolich and Hesham Mourad 2 and in the first row, Sylvie Vidinha, Olivia Struyven and myself, good 3 morning. -

Why Millennials Need More 'Frozen' Love: Column 2/18/15 6:48 AM
Why millennials need more 'Frozen' love: Column 2/18/15 6:48 AM Why millennials need more 'Frozen' love: Column Amber Lapp 1:58 p.m. EST February 17, 2015 What Disney's animated hit can teach fearful young people about relationships. A few weeks ago I spent a day sick in bed, drinking green tea with spoonfuls of honey and spritzes of lemon by the mug-full, and trying to rest while my three-year-old jumped on the bed and occasionally on top of me, too. That's when I decided to put in the Disney movie that everyone has been talking about for the last year — we've been invited to Frozen movie nights in the park and brought Frozen dolls as gifts to Frozen-themed birthday parties — but I had yet to see it. So my son and I snuggled up to watch the highest-grossing animated film (http://www.hollywoodreporter.com/news/box-office-milestone-frozen-becomes-692156) of all time. (Photo: Uncredited, AP) I was riveted. Not only because of the animation and music, but because of the way this movie tells a story similar to the one that my husband and I heard while interviewing young adults for the Love and Marriage in Middle America Project (http://ifstudies.org/about/). No wonder all the young moms (and dads) I know love Frozen: it tells the story they've lived when it comes to love. Granted, none of our interviewees mentioned trolls or snow queens or talking snowmen — but the experiences and behaviors of the movie's two female protagonists, princess sisters Anna and Elsa, do reflect those of the young adults we interviewed in an important way. -

For People with Aplastic Anemia, Fresh Cells Rather Than Frozen
RESEARCH NEWS For people with aplastic anemia, fresh cells rather than frozen are better for blood and marrow transplant New research suggests people with aplastic anemia do better when blood and marrow transplant (BMT) uses fresh, rather than frozen cells. BMT can cure aplastic anemia, which causes the body to stop making enough blood and marrow cells. However, during the coronavirus (COVID-19) pandemic, restrictions make it harder for donors to travel to a medical center to donate cells for BMT. It’s also harder for couriers to deliver the fresh cells to the patient. Since patients prepare for BMT days beforehand, it is critical that the donated cells arrive on time. Learn more about Doctors wanted to know whether frozen cells would work as well as fresh • COVID-19 FAQs, from cells. It is possible to collect, preserve, and very slowly freeze the cells. This BeTheMatch.org is called cryopreservation. The frozen cells can be stored until needed, • More study summaries at and then thawed. cibmtr.org Scientists looked at medical records of about 250 people with aplastic About this research summary anemia who received BMT during 2013-2019. About 1 in 5 of these This information is provided on people got BMT with previously frozen cells. They were compared to behalf of the Consumer Advocacy similar people who got fresh cells. Committee of the CIBMTR® (Center for International Blood and Marrow A year after transplant: Transplant Research®). • 73% (7 out of 10) of people who got frozen cells were likely to be alive. Source • 91% (9 out of 10) of people who got fresh cells were likely to be alive. -

Blank Space” Video Demonstrates Culture’S Love/Hate Relationship with Taylor Swift
“Blank Space” video demonstrates culture’s love/hate relationship with Taylor Swift People that know me well know that I struggle to find a common ground between Taylor Swift and myself. She’s genius, yet infuriating. She’s smart, yet oh so dumb. She’s wise beyond her years, yet stuck in the world of a 12-year-old. You either love or hate Swift. The media has made her into a debate of whether or not pop music’s biggest superstar is really all she’s cracked up to be. I stand frozen in the middle of this debate. If I say I like Swift I’m seen as a silly girl. If I say I don’t like her it’s as if I don’t understand pop music at all. Swift’s newly released video for her next single “Blank Space” hit the Internet hard Monday afternoon. “Blank Space” is arguably the best song on her new album “1989” (way better than “Shake It Off” and less Harry Styles than “Out of the Woods”). The video perfectly sums up mine, and what I assume is the mass culture’s love/hate relationship with the singer. “Blank Space” takes place in a Gatsby-like mansion with Swift and a really attractive gentleman starting a relationship. They’re shown riding horses, having fancy dinners, and enjoying picnics. At one point Swift paints a creepy picture of her new love. You know, normal relationship stuff. Then the relationship seems to go south. Attractive man is calling other girls. Swift is getting jealous. -

Hold It High (Cadence) on the Road Again the U.S
Hold It High (cadence) On the Road Again The U.S. Air Force Willie Nelson Brave Never Gonna Give You Up Sara Bareilles Rick Astley My Hero Home Foo Fighters Phillip Phillips Fight Song We Are The Champions Rachel Platten Queen Can’t Stop the Feeling (from Trolls) When Can I See You Again? (from Wreck-It Ralph) Justin Timberlake Owl City Dog Days Are Over Rise Up Florence & The Machine Andra Day Don’t You Worry ‘Bout A Thing (from SING) Holding Out For A Hero (from Footloose) Tori Kelly Bonnie Tyler Heroes (We Could Be) Firework Alesso, Tove Lo Katy Perry Daisies You’ll Always Find Your Way Back Home Katy Perry Hannah Montana How Far I’ll Go (from Moana) You Got It (The Right Stuff) Auli’I Cravalho New Kids On The Block Friends Are Family (from LEGO Batman Movie) Wild Things Oh, Hush!, Jeff Lewis, Will Arnett Alessia Cara 355th Force Support Squadron Marketing // Davis-Monthan Air Force Base Castle On The Hill Shake It Off Ed Sheeran Taylor Swift How Far We’ve Come Something To Be Proud Of Matchbox Twenty Montogomery Gentry I Will Wait I’m Still Standing Mumford & Sons Elton John Keep Your Head Up Go The Distance (from Hercules) Andy Grammar Roger Bart Leaving, On A Jet Plane Scars To Your Beautiful John Denver Alessia Cara Miles Apart We Know The Way (from Moana) Yellowcard Opetaia Foa’I, Lin-Manuel Miranda Into The Unknown (from Frozen 2) Part Of Me Idina Menzel, AURORA Katy Perry Budapest Just Around The Riverbend (from Pocahontas) George Ezra Judy Kuhn Boomerang I Will Survive JoJo Siwa Gloria Gaynor This Is Me (from The Greatest Showman) Tightrope (feat. -
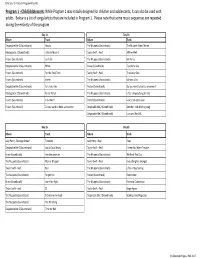
Program 1 ‐ Child/Adolescent: While Program 1 Was Initially Designed for Children and Adolescents, It Can Also Be Used with Adults
Safe Sound Protocol Program Playlists Program 1 ‐ Child/Adolescent: While Program 1 was initially designed for children and adolescents, it can also be used with adults. Below is a list of songs/artists that are included in Program 1. Please note that some music sequences are repeated during the entirety of the program. Day 1a Day 1b Album Track Album Track Despicable Me 2 (Soundtrack) Happy The Muppets (Soundtrack) The Muppet Show Theme Madagascar 2 (Soundtrack) I Like to Move It Taylor Swift ‐ Red All Too Well Frozen (Soundtrack) Let It Go The Muppets (Soundtrack) Me Party Despicable Me 2 (Soundtrack) YMCA Brave (Soundtrack) Touch the Sky Frozen (Soundtrack) For the First Time Taylor Swift ‐ Red The Lucky One Frozen (Soundtrack) Vuelie The Muppets (Soundtrack) Me and Julio Despicable Me 2 (Soundtrack) Fun, Fun, Fun Frozen (Soundtrack) Do you want to build a snowman? Madagascar 2 (Soundtrack) Party! Party! The Muppets (Soundtrack) Life’s a Happy Song (finale) Frozen (Soundtrack) In Summer Frozen (Soundtrack) Love is an open door Frozen (Soundtrack) Do you want to build a snowman Despicable Me 2 (Soundtrack) Another Irish drinking song Despicable Me 2 (Soundtrack) Lucy and the AVL Day 2a Day 2b Album Track Album Track Katy Perry ‐ Teenage Dream Firework Katy Perry ‐ Roar Roar Despicable Me 2 (Soundtrack) Just a Cloud Away Taylor Swift ‐ Red I Knew You Were Trouble Brave (Soundtrack) Into the open air The Muppets (Soundtrack) We Built This City The Muppets (Soundtrack) Man or Muppet Taylor Swift ‐ Red Everything has changed Taylor Swift -

ARTIST INDEX(Continued)
ChartARTIST Codes: CJ (Contemporary Jazz) INDEXINT (Internet) RBC (R&B/Hip-Hop Catalog) –SINGLES– DC (Dance Club Songs) LR (Latin Rhythm) RP (Rap Airplay) –ALBUMS– CL (Traditional Classical) JZ (Traditional Jazz) RBL (R&B Albums) A40 (Adult Top 40) DES (Dance/Electronic Songs) MO (Alternative) RS (Rap Songs) B200 (The Billboard 200) CX (Classical Crossover) LA (Latin Albums) RE (Reggae) AC (Adult Contemporary) H100 (Hot 100) ODS (On-Demand Songs) STS (Streaming Songs) BG (Bluegrass) EA (Dance/Electronic) LPA (Latin Pop Albums) RLP (Rap Albums) ARB (Adult R&B) HA (Hot 100 Airplay) RB (R&B Songs) TSS (Tropical Songs) BL (Blues) GA (Gospel) LRS (Latin Rhythm Albums) RMA (Regional Mexican Albums) CA (Christian AC) HD (Hot Digital Songs) RBH (R&B Hip-Hop) XAS (Holiday Airplay) APR CA (Country) HOL (Holiday) NA (New Age) TSA (Tropical Albums) CS (Country) HSS (Hot 100 Singles Sales) RKA (Rock Airplay) XMS (Holiday Songs) CC (Christian) HS (Heatseekers) PCA (Catalog) WM (World) CST (Christian Songs) LPS (Latin Pop Songs) RMS (Regional Mexican Songs) 24 CCA (Country Catalog) IND (Independent) RBA (R&B/Hip-Hop) DA (Dance/Mix Show Airplay) LT (Hot Latin Songs) RO (Hot Rock Songs) 2021 $NOT HS 19, 22 JUSTIN BIEBER B200 3; CC 8; DLP 11; RBL 25; J. COLE B200 68; PCA 14; RBA 37 LUIS FIGUEROA TSS 21 STEPHEN HOUGH CL 11 LYDIA LAIRD CA 29; CST 33 21 SAVAGE B200 103; RBH 49 A40 13, 26; AC 9, 16, 20; CST 23, 26, 35, 36, KEYSHIA COLE ARB 14 FINNEAS A40 36; AK 18; RO 20 WHITNEY HOUSTON B200 197; RBL 22 LAKE STREET DIVE RKA 46 24KGOLDN B200 65; A40 4; AC 25;