A Hierarchical Bayesian Model of Pitch Framing
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Reign Men Taps Into a Compelling Oral History of Game 7 in the 2016 World Series
Reign Men taps into a compelling oral history of Game 7 in the 2016 World Series. Talking Cubs heads all top CSN Chicago producers need in riveting ‘Reign Men’ By George Castle, CBM Historian Posted Thursday, March 23, 2017 Some of the most riveting TV can be a bunch of talking heads. The best example is enjoying multiple airings on CSN Chicago, the first at 9:30 p.m. Monday, March 27. When a one-hour documentary combines Theo Epstein and his Merry Men of Wrigley Field, who can talk as good a game as they play, with the video skills of world-class producers Sarah Lauch and Ryan McGuffey, you have a must-watch production. We all know “what” happened in the Game 7 Cubs victory of the 2016 World Series that turned from potentially the most catastrophic loss in franchise history into its most memorable triumph in just a few minutes in Cleveland. Now, thanks to the sublime re- porting and editing skills of Lauch and McGuffey, we now have the “how” and “why” through the oral history contained in “Reign Men: The Story Behind Game 7 of the 2016 World Series.” Anyone with sense is tired of the endless shots of the 35-and-under bar crowd whooping it up for top sports events. The word here is gratuitous. “Reign Men” largely eschews those images and other “color” shots in favor of telling the story. And what a tale to tell. Lauch and McGuffey, who have a combined 20 sports Emmy Awards in hand for their labors, could have simply done a rehash of what many term the greatest Game 7 in World Series history. -

2018 Game Notes
asdasdfasdf 2018 GAME NOTES American League East Champions 1985, 1989, 1991, 1992, 1993, 2015 American League Champions 1992, 1993 World Series Champions 1992, 1993 Toronto Blue Jays Baseball Media Department Follow us on Twitter @BlueJaysPR NEW YORK YANKEES (0-0) vs. TORONTO BLUE JAYS (0-0) RHP Luis Severino (2017: 14-6, 2.98) vs. LHP J.A. Happ (2017: 10-11, 3.53) Game #1 Home #1 (0-0) March 29, 2018 3:37pm TV: SNET RADIO: SN590 2018 AT A GLANCE ON THE HOME FRONT: Record (2017) ..............................................................76-86, 4th, 17.0 GB This afternoon, Toronto kicks off the 2018 campaign with the opener of a Home Attendance (Total & Average-2017) ......................3,203,886/39,554 four-game series against the Yankees...The Jays last started a season Sellouts (2017) ........................................................................................17 with a four-game set at home in 2009, taking three of four games from 2017 Season Record after 1 Game .......................................................0-1 the Tigers. 2017 Season Record after 2 Games ......................................................0-2 The Blue Jays went 42-39 at Rogers Centre for their 4th consecutive Come From Behind Wins (2017) .............................................................39 winning season at home…Scored an average of 4.10 runs/game at Last Shutout by Blue Jays ................................4-0, Aug. 10, 2017 vs. NYY home, the lowest in the AL (27th in MLB)…The team’s 332 runs in home Last Shutout by Opponent ...............................4-0, Sept. 29, 2017 at NYY affairs was its lowest total since 1997 (326). Under JOHN GIBBONS .................................................................720-700 BLUE JAYS vs. YANKEES: vs. RHS/LHS (2017) .................................................................58-62/17-24 All-Time: 277-336...All-Time, Rogers Centre: 116-110...2017: 10-9 Blue Jays/Opponents Scoring First (2017) ..............................42-34/33-51 Toronto is 1-2 all-time vs. -

Chicago White Sox 2018 Spring Training Game Notes
CHICAGO WHITE SOX 2018 SPRING TRAINING GAME NOTES © 2018 Chicago White Sox whitesox.com l loswhitesox.com l whitesoxpressbox.com l @whitesox CHICAGO WHITE SOX (15-12-3) at CHARLOTTE KNIGHTS (0-0) WHITE SOX SPRING SCHEDULE/RESULTS: 16-12-3 RHP Reynaldo López (1-1, 3.29) vs. RHP Donn Roach (NR) Day Date Opponent Result Attendance Record Fri. 2/23 at LA Dodgers L, 5-13 6,813 0-1 Game #32 | Road # 17 l Monday, March 26 l Charlotte, N.C. Sat. 2/24 at Seattle W, 5-3 5,107 1-1 Sun. 2/25 Cincinnati W, 8-5 2,703 2-1 WHITE SOX AT A GLANCE Mon. 2/26 Oakland W, 7-6 2,826 3-1 l The Chicago White Sox have won nine of the last 14 games (one tie) as they play an exhibition Tue. 2/27 at Cubs L, 5-6 10,769 3-2 game this evening vs. Class AAA Charlotte at BB&T Ballpark. Wed. 2/28 Texas W, 5-4 2,360 4-2 Thu. 3/1 at Cincinnati L, 7-8 2,271 4-3 l RHP Reynaldo López will make his fifth start this spring … he suffered the loss in his last start Fri. 3/2 LA Dodgers L, 6-7 7,423 4-4 on 3/16 vs. the Cubs, allowing four runs on eight hits over 4.1 IP. Sat. 3/3 at Kansas City W, 9-5 5,793 5-4 l The White Sox rank among spring leaders in triples (1st, 15), runs scored (4th, 187), RBI (4th, Sun. -

2020 Topps Chrome Sapphire Edition .Xls
SERIES 1 1 Mike Trout Angels® 2 Gerrit Cole Houston Astros® 3 Nicky Lopez Kansas City Royals® 4 Robinson Cano New York Mets® 5 JaCoby Jones Detroit Tigers® 6 Juan Soto Washington Nationals® 7 Aaron Judge New York Yankees® 8 Jonathan Villar Baltimore Orioles® 9 Trent Grisham San Diego Padres™ Rookie 10 Austin Meadows Tampa Bay Rays™ 11 Anthony Rendon Washington Nationals® 12 Sam Hilliard Colorado Rockies™ Rookie 13 Miles Mikolas St. Louis Cardinals® 14 Anthony Rendon Angels® 15 San Diego Padres™ 16 Gleyber Torres New York Yankees® 17 Franmil Reyes Cleveland Indians® 18 Minnesota Twins® 19 Angels® Angels® 20 Aristides Aquino Cincinnati Reds® Rookie 21 Shane Greene Atlanta Braves™ 22 Emilio Pagan Tampa Bay Rays™ 23 Christin Stewart Detroit Tigers® 24 Kenley Jansen Los Angeles Dodgers® 25 Kirby Yates San Diego Padres™ 26 Kyle Hendricks Chicago Cubs® 27 Milwaukee Brewers™ Milwaukee Brewers™ 28 Tim Anderson Chicago White Sox® 29 Starlin Castro Washington Nationals® 30 Josh VanMeter Cincinnati Reds® 31 American League™ 32 Brandon Woodruff Milwaukee Brewers™ 33 Houston Astros® Houston Astros® 34 Ian Kinsler San Diego Padres™ 35 Adalberto Mondesi Kansas City Royals® 36 Sean Doolittle Washington Nationals® 37 Albert Almora Chicago Cubs® 38 Austin Nola Seattle Mariners™ Rookie 39 Tyler O'neill St. Louis Cardinals® 40 Bobby Bradley Cleveland Indians® Rookie 41 Brian Anderson Miami Marlins® 42 Lewis Brinson Miami Marlins® 43 Leury Garcia Chicago White Sox® 44 Tommy Edman St. Louis Cardinals® 45 Mitch Haniger Seattle Mariners™ 46 Gary Sanchez New York Yankees® 47 Dansby Swanson Atlanta Braves™ 48 Jeff McNeil New York Mets® 49 Eloy Jimenez Chicago White Sox® Rookie 50 Cody Bellinger Los Angeles Dodgers® 51 Anthony Rizzo Chicago Cubs® 52 Yasmani Grandal Chicago White Sox® 53 Pete Alonso New York Mets® 54 Hunter Dozier Kansas City Royals® 55 Jose Martinez St. -

Colorado Springs Sky
COLORADO SPRINGS SKY SOX 2016 GAME NOTES SATURDAY SEPTEMBER 3, 2016 - 6:08 PM (MDT) Colorado Springs Sky Sox Public Relations Department • Director: Nick Dobreff • (616) 485-3913 • [email protected] Director of Broadcasting • Dan Karcher • [email protected] www.SkySox.com Facebook.com/SkySoxBaseball @SkySox SkySoxBaseball TONIGHT’S STARTING PITCHERS RECORD: 67-68 Colorado Springs: LHP Wei-Chung Wang (1-2, 3 .80) VS. Iowa: RHP Josh Collmenter (0-0, 1 .96) SKY SOX SEASON AT A GLANCE Game Number . 136 Home Record . 41-27 Road Game Number . 68 Road Record . 26-41 Overall Record . 67-68 vs . RHP: . 51-54 vs . American Northern . 23-21 vs . LHP . 16-14 vs . American Southern . 35-28 Night . 52-52 vs . Pacific Northern . 3-12 Day . 15-16 vs . Pacific Southern . 6-7 Last 10 . 5-5 One-Run Games . .. 20-20 Current Streak . L1 RECORD: 64-76 LAST TIME OUT BRINSANITY HITS COLORADO SPRINGS SKY SOX AMONG THE LEAGUE LEADERS u The Sky Sox dropped game one of their four-game series u OF Lewis Brinson has burst onto the scene since being WALKS Reed 4th 73 against the Iowa Cubs by a score of 3-2. traded from Texas to Milwaukee on August 1st in exchange for C ERA Suter 7th 3.50 u INF Garrett Cooper led the Sky Sox offense with two hits Jonathan Lucroy. In 21 games with the Sky Sox, he’s hitting .395 SAVES Magnifico 4th 18 going 2-for-4. He’s hitting .379 (11-for-29) with two home runs, (32-for-81) with four HR, eight doubles, 13 runs, 20 RBI. -
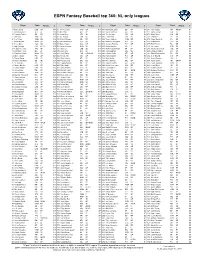
NL-Only Leagues
ESPN Fantasy Baseball top 360: NL-only leagues Player Team All pos. $ Player Team All pos. $ Player Team All pos. $ Player Team All pos. $ 1. Mookie Betts LAD OF $44 91. Joc Pederson CHC OF $14 181. MacKenzie Gore SD SP $7 271. John Curtiss MIA RP/SP $1 2. Ronald Acuna Jr. ATL OF $39 92. Will Smith ATL RP $14 182. Stefan Crichton ARI RP $6 272. Josh Fuentes COL 1B $1 3. Fernando Tatis Jr. SD SS $37 93. Austin Riley ATL 3B $14 183. Tim Locastro ARI OF $6 273. Wade Miley CIN SP $1 4. Juan Soto WSH OF $36 94. A.J. Pollock LAD OF $14 184. Lucas Sims CIN RP $6 274. Chad Kuhl PIT SP $1 5. Trea Turner WSH SS $32 95. Devin Williams MIL RP $13 185. Tanner Rainey WSH RP $6 275. Anibal Sanchez FA SP $1 6. Jacob deGrom NYM SP $30 96. German Marquez COL SP $13 186. Madison Bumgarner ARI SP $6 276. Rowan Wick CHC RP $1 7. Trevor Story COL SS $30 97. Raimel Tapia COL OF $13 187. Gregory Polanco PIT OF $6 277. Rick Porcello FA SP $0 8. Cody Bellinger LAD OF/1B $30 98. Carlos Carrasco NYM SP $13 188. Omar Narvaez MIL C $6 278. Jon Lester WSH SP $0 9. Freddie Freeman ATL 1B $29 99. Gavin Lux LAD 2B $13 189. Anthony DeSclafani SF SP $6 279. Antonio Senzatela COL SP $0 10. Christian Yelich MIL OF $29 100. Zach Eflin PHI SP $13 190. Josh Lindblom MIL SP $6 280. -

A Bayesian Hierarchical Model to Estimate the Framing Ability of Major League Baseball Catchers
A Bayesian Hierarchical Model To Estimate the Framing Ability of Major League Baseball Catchers Sameer K. Deshpande and Abraham J. Wyner Statistics Department, The Wharton School University of Pennsylvania 26 September 2015 Introduction • What exactly is framing? I A catcher's effect on the likelihood a taken pitch is called a strike. • Should we even care about framing? I Lots of attention in popular presst I Several articles on Baseball Prospectus and Hardball Times I \Good framer" can save ∼ 15 - 25 runs per season. I Teams seem to care: Hank Conger, Russell Martin Deshpande & Wyner Catcher Framing NESSIS 2015 2 / 15 Fundamental Question and Our Contribution For any given taken pitch, what is the catcher's effect on likelihood of pitch being called strike over and above factors like: • Pitch Location • Pitch Context: Count, base runners, score differential, etc. • Pitch Participants: batter, pitcher, umpire Our contributions: • Hierarchical Bayesian logistic regression model of called strike probability • Value of a called strike as function of count • Uncertainty estimates of framing impact (runs saved on average) Deshpande & Wyner Catcher Framing NESSIS 2015 3 / 15 PITCHf/x Data PITCHf/x data scraped from MLB Advanced Media: • Horizontal and vertical coordinate of pitch as it crosses plate • Approximate vertical boundaries for the strike zone • Umpire, pitcher, catcher, batter identities • Count Focus only on the 320,308 taken pitches within 1 ft. of the strike zone. Deshpande & Wyner Catcher Framing NESSIS 2015 4 / 15 Parameterizing Pitch Location (a) Distance from strike zone, R (b) Angles from horizontal and vertical Figure: R;'1;'2 for RHB Deshpande & Wyner Catcher Framing NESSIS 2015 5 / 15 Bayesian Logistic Regression Model For umpire u, log-odds of calling a strike is a linear function of: R;'1;'2; and indicators for batter, catcher, pitcher, and count Let Θ(u) be vector of covariate partial effects. -
Coos Bay Chapel, 541- Dissipate
C M C M Y K Y K FREEZE DRY A SHIP? ROOKIE STARTER College will try to rebuild wreck, A7 Browns turn to Weeden at QB, B1 Serving Oregon’s South Coast Since 1878 WEDNESDAY,AUGUST 15, 2012 theworldlink.com I 75¢ ACS Denise Cacace, left, and Jan settles Dilley work Confidence through their tai chi exercises wage-hour Tuesday at the North Bend complaint Senior Center. builder I File claims by Sept. 1 BY GAIL ELBER The World If you worked for call center company ACS in Oregon between April 2, 2005, and April 25, 2012, you might be entitled to some money as part of the company’s settlement of a class action lawsuit concerning its wage and hour practices. Spread the word to other former ACS employees — and don’t delay, because any money that’s not claimed by Sept. 1 will go back to ACS. The suit, Bell et al. v. Affiliated Computer Services Inc., ACS Commercial Solutions Inc., and Livebridge Inc., was filed in December 2009 by four ACS employees. ACS settled on July 12. The employees said ACS had required them to be at work with- out a computer workstation avail- able on which to clock in, and that the company’s manual time cor- rection forms didn’t capture all work time. They also said ACS didn’t pay employees all the bonuses they earned and didn’t correctly calculate overtime pay. In the settlement agreement, ACS said it denies the plantiffs’ allegations, but it agreed to a set- tlement because of the expense of defending against them. -

List of Players in Apba's 2018 Base Baseball Card
Sheet1 LIST OF PLAYERS IN APBA'S 2018 BASE BASEBALL CARD SET ARIZONA ATLANTA CHICAGO CUBS CINCINNATI David Peralta Ronald Acuna Ben Zobrist Scott Schebler Eduardo Escobar Ozzie Albies Javier Baez Jose Peraza Jarrod Dyson Freddie Freeman Kris Bryant Joey Votto Paul Goldschmidt Nick Markakis Anthony Rizzo Scooter Gennett A.J. Pollock Kurt Suzuki Willson Contreras Eugenio Suarez Jake Lamb Tyler Flowers Kyle Schwarber Jesse Winker Steven Souza Ender Inciarte Ian Happ Phillip Ervin Jon Jay Johan Camargo Addison Russell Tucker Barnhart Chris Owings Charlie Culberson Daniel Murphy Billy Hamilton Ketel Marte Dansby Swanson Albert Almora Curt Casali Nick Ahmed Rene Rivera Jason Heyward Alex Blandino Alex Avila Lucas Duda Victor Caratini Brandon Dixon John Ryan Murphy Ryan Flaherty David Bote Dilson Herrera Jeff Mathis Adam Duvall Tommy La Stella Mason Williams Daniel Descalso Preston Tucker Kyle Hendricks Luis Castillo Zack Greinke Michael Foltynewicz Cole Hamels Matt Harvey Patrick Corbin Kevin Gausman Jon Lester Sal Romano Zack Godley Julio Teheran Jose Quintana Tyler Mahle Robbie Ray Sean Newcomb Tyler Chatwood Anthony DeSclafani Clay Buchholz Anibal Sanchez Mike Montgomery Homer Bailey Matt Koch Brandon McCarthy Jaime Garcia Jared Hughes Brad Ziegler Daniel Winkler Steve Cishek Raisel Iglesias Andrew Chafin Brad Brach Justin Wilson Amir Garrett Archie Bradley A.J. Minter Brandon Kintzler Wandy Peralta Yoshihisa Hirano Sam Freeman Jesse Chavez David Hernandez Jake Diekman Jesse Biddle Pedro Strop Michael Lorenzen Brad Boxberger Shane Carle Jorge de la Rosa Austin Brice T.J. McFarland Jonny Venters Carl Edwards Jackson Stephens Fernando Salas Arodys Vizcaino Brian Duensing Matt Wisler Matt Andriese Peter Moylan Brandon Morrow Cody Reed Page 1 Sheet1 COLORADO LOS ANGELES MIAMI MILWAUKEE Charlie Blackmon Chris Taylor Derek Dietrich Lorenzo Cain D.J. -

WHITE SOX HEADLINES of OCTOBER 29, 2018 “Chris Sale
WHITE SOX HEADLINES OF OCTOBER 29, 2018 “Chris Sale closes out World Series victory for Red Sox” … Tim Stebbins, NBC Sports Chicago “Kevan Smith heads to Angels on waiver claim, clarifying White Sox catching situation” … Vinnie Duber, NBC Sports Chicago “Happy Birthday, Daniel Palka” … Chris Kamka, NBC Sports Chicago “Matt Davidson envisions specific situations where he can pitch out of bullpen in 2019” … Tim Stebbins, NBC Sports Chicago “Remember That Guy?: Willie Harris” … Chris Kamka, NBC Sports Chicago “White Sox outright 3 players, including pitcher Danny Farquhar” … Daryl Van Schouwen, Sun-Times “Angels claim Smith; White Sox outright Farquhar, Scahill, LaMarre” … Scot Gregor, Daily Herald “A roster crunch ends Kevan Smith’s run on the South Side, but the door is still open for a Danny Farquhar comeback” … James Fegan, The Athletic Chris Sale closes out World Series victory for Red Sox By Tim Stebbins / NBC Sports Chicago / October 26, 2018 Chris Sale never tasted the postseason during his seven seasons with the White Sox. Sunday, he closed out the World Series for the Red Sox, winning his first championship. The Red Sox called on Sale to pitch the 9th inning of Game 5 of the Fall Classic on Sunday, and the lean left-hander did not disappoint. Sale struck out Justin Turner, Kike Hernández and Manny Machado in-order, clinching the Red Sox fourth championship in 15 seasons. While White Sox fans surely wish Sale helped bring another championship to the South Side, congratulations are in order for the former White Sox ace. And, who knows? A few years down the line, maybe Michael Kopech, who the White Sox acquired from Boston in the Sale trade, will be on the mound in a World Series' clincher for the White Sox. -

2017 Game Notes
2017 GAME NOTES American League East Champions 1985, 1989, 1991, 1992, 1993, 2015 American League Champions 1992, 1993 World Series Champions 1992, 1993 Toronto Blue Jays Baseball Media Department Follow us on Twitter @BlueJaysPR Game #14, Home #8 (1-6), BOSTON RED SOX (9-5) at TORONTO BLUE JAYS (2-11), Wednesday, April 19, 2017 PROBABLE PITCHING MATCHUPS: (All Times Eastern) Wednesday, April 19 vs. Boston Red Sox, 7:07 pm…RHP Rick Porcello (1-1, 7.56) vs. LHP Francisco Liriano (0-1, 9.00) Thursday, April 20 vs. Boston Red Sox, 12:37 pm…LHP Chris Sale (1-1, 1.25) vs. RHP Marco Estrada (0-1, 3.50) ON THE HOMEFRONT: 2017 AT A GLANCE nd Record ...................................................................... 2-11, 5th, 6.5 GB Tonight, TOR continues a 9G homestand with the 2 of a 3G set vs. Home Attendance (Total & Average) ......................... 259,091/37,013 BOS…Are 1-6 on the homestand after dropping the series opener Sellouts (2017) .................................................................................. 1 vs. BOS, 8-7…Have been outscored 34-21 over their first seven 2016 Season (Record after 13 Games) ......................................... 6-7 games at home while averaging 3.00 R/G over that stretch…After 2016 Season (Record after 14 Games) ......................................... 7-7 seven games in 2016 the Jays had averaged 4.57 R/G (32 total 2016 Season (Hm. Att.) – After 7 games ............................... 269,413 runs)…Dropped their first four games of their home schedule for just the 2nd time in club history (0-8 in 2004)…Are looking to avoid losing 2016 Season (Hm. Att.) – After 8 games .............................. -

April 9, 2015 • Chicago Tribune, Cubs Push the Right Motivational
April 9, 2015 Chicago Tribune, Cubs push the right motivational buttons en route to 1st victory http://www.chicagotribune.com/sports/baseball/cubs/ct-jake-arrieta-report-cubs-cardinals-spt-0409- 20150408-story.html Chicago Tribune, Jake Arrieta draws comparisons to Jane Fonda http://www.chicagotribune.com/sports/baseball/cubs/chi-jake-arrieta-works-out-20150408-story.html Chicago Tribune, Cubs not considering moving home games http://www.chicagotribune.com/sports/baseball/cubs/chi-cubs-not-considering-moving-home-games- 20150408-story.html Chicago Tribune, Wednesday's recap: Cubs 2, Cardinals 0 http://www.chicagotribune.com/sports/baseball/cubs/ct-gameday-cubs-cardinals-spt-0409-20150408- story.html Chicago Tribune, Colorado homecoming for Joe Maddon http://www.chicagotribune.com/sports/baseball/cubs/chi-joe-maddon-returns-20150408-story.html Chicago Tribune, Jon Lester believes pickoff issue 'blown out of proportion' http://www.chicagotribune.com/sports/baseball/cubs/chi-jon-lester-miffed-20150408-story.html Chicago Tribune, Cubs' C.J. Edwards could be on faster track as reliever http://www.chicagotribune.com/sports/baseball/cubs/chi-cj-edwards-moved-to-reliever-20150408-story.html Chicago Sun-Times, Jon Lester says throwing to bases no problem--after practicing it in pen http://chicago.suntimes.com/baseball/7/71/511065/jon-lester-dismisses-issue-throwing-bases-session- practicing Chicago Sun-Times, Jake Arrieta shines in his 2015 debut, blanks Cardinals in win http://chicago.suntimes.com/baseball/7/71/511044/jake-arrieta-shines-2015-debut-blanks-cardinals-win