On Axioms and Images in the History of Mathematics
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Canada Archives Canada Published Heritage Direction Du Branch Patrimoine De I'edition
Rhetoric more geometrico in Proclus' Elements of Theology and Boethius' De Hebdomadibus A Thesis submitted in Candidacy for the Degree of Master of Arts in Philosophy Institute for Christian Studies Toronto, Ontario By Carlos R. Bovell November 2007 Library and Bibliotheque et 1*1 Archives Canada Archives Canada Published Heritage Direction du Branch Patrimoine de I'edition 395 Wellington Street 395, rue Wellington Ottawa ON K1A0N4 Ottawa ON K1A0N4 Canada Canada Your file Votre reference ISBN: 978-0-494-43117-7 Our file Notre reference ISBN: 978-0-494-43117-7 NOTICE: AVIS: The author has granted a non L'auteur a accorde une licence non exclusive exclusive license allowing Library permettant a la Bibliotheque et Archives and Archives Canada to reproduce, Canada de reproduire, publier, archiver, publish, archive, preserve, conserve, sauvegarder, conserver, transmettre au public communicate to the public by par telecommunication ou par Plntemet, prefer, telecommunication or on the Internet, distribuer et vendre des theses partout dans loan, distribute and sell theses le monde, a des fins commerciales ou autres, worldwide, for commercial or non sur support microforme, papier, electronique commercial purposes, in microform, et/ou autres formats. paper, electronic and/or any other formats. The author retains copyright L'auteur conserve la propriete du droit d'auteur ownership and moral rights in et des droits moraux qui protege cette these. this thesis. Neither the thesis Ni la these ni des extraits substantiels de nor substantial extracts from it celle-ci ne doivent etre imprimes ou autrement may be printed or otherwise reproduits sans son autorisation. reproduced without the author's permission. -

Two Editions of Ibn Al-Haytham's Completion of the Conics
Historia Mathematica 29 (2002), 247–265 doi:10.1006/hmat.2002.2352 Two Editions of Ibn al-Haytham’s Completion of the Conics View metadata, citation and similar papers at core.ac.uk brought to you by CORE Jan P. Hogendijk provided by Elsevier - Publisher Connector Mathematics Department, University of Utrecht, P.O. Box 80.010, 3508 TA Utrecht, Netherlands E-mail: [email protected] The lost Book VIII of the Conics of Apollonius of Perga (ca. 200 B.C.) was reconstructed by the Islamic mathematician Ibn al-Haytham (ca. A.D. 965–1041) in his Completion of the Conics. The Arabic text of this reconstruction with English translation and commentary was published as J. P. Hogendijk, Ibn al-Haytham’s Completion of the Conics (New York: Springer-Verlag, 1985). In a new Arabic edition with French translation and commentary (R. Rashed, Les mathematiques´ infinitesimales´ du IXe au XIe siecle.´ Vol. 3., London: Al-Furqan Foundation, 2000), it was claimed that my edition is faulty. In this paper the similarities and differences between the two editions, translations, and commentaries are discussed, with due consideration for readers who do not know Arabic. The facts will speak for themselves. C 2002 Elsevier Science (USA) C 2002 Elsevier Science (USA) C 2002 Elsevier Science (USA) 247 0315-0860/02 $35.00 C 2002 Elsevier Science (USA) All rights reserved. 248 JAN P. HOGENDIJK HMAT 29 AMS subject classifications: 01A20, 01A30. Key Words: Ibn al-Haytham; conic sections; multiple editions; Rashed. 1. INTRODUCTION The Conics of Apollonius of Perga (ca. 200 B.C.) is one of the fundamental texts of ancient Greek geometry. -

History of Mathematics in Mathematics Education. Recent Developments Kathy Clark, Tinne Kjeldsen, Sebastian Schorcht, Constantinos Tzanakis, Xiaoqin Wang
History of mathematics in mathematics education. Recent developments Kathy Clark, Tinne Kjeldsen, Sebastian Schorcht, Constantinos Tzanakis, Xiaoqin Wang To cite this version: Kathy Clark, Tinne Kjeldsen, Sebastian Schorcht, Constantinos Tzanakis, Xiaoqin Wang. History of mathematics in mathematics education. Recent developments. History and Pedagogy of Mathematics, Jul 2016, Montpellier, France. hal-01349230 HAL Id: hal-01349230 https://hal.archives-ouvertes.fr/hal-01349230 Submitted on 27 Jul 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. HISTORY OF MATHEMATICS IN MATHEMATICS EDUCATION Recent developments Kathleen CLARK, Tinne Hoff KJELDSEN, Sebastian SCHORCHT, Constantinos TZANAKIS, Xiaoqin WANG School of Teacher Education, Florida State University, Tallahassee, FL 32306-4459, USA [email protected] Department of Mathematical Sciences, University of Copenhagen, Denmark [email protected] Justus Liebig University Giessen, Germany [email protected] Department of Education, University of Crete, Rethymnon 74100, Greece [email protected] Department of Mathematics, East China Normal University, China [email protected] ABSTRACT This is a survey on the recent developments (since 2000) concerning research on the relations between History and Pedagogy of Mathematics (the HPM domain). Section 1 explains the rationale of the study and formulates the key issues. -

By the Persian Mathematician and Engineer Abubakr
1 2 The millennium old hydrogeology textbook “The Extraction of Hidden Waters” by the Persian 3 mathematician and engineer Abubakr Mohammad Karaji (c. 953 – c. 1029) 4 5 Behzad Ataie-Ashtiania,b, Craig T. Simmonsa 6 7 a National Centre for Groundwater Research and Training and College of Science & Engineering, 8 Flinders University, Adelaide, South Australia, Australia 9 b Department of Civil Engineering, Sharif University of Technology, Tehran, Iran, 10 [email protected] (B. Ataie-Ashtiani) 11 [email protected] (C. T. Simmons) 12 13 14 15 Hydrology and Earth System Sciences (HESS) 16 Special issue ‘History of Hydrology’ 17 18 Guest Editors: Okke Batelaan, Keith Beven, Chantal Gascuel-Odoux, Laurent Pfister, and Roberto Ranzi 19 20 1 21 22 Abstract 23 We revisit and shed light on the millennium old hydrogeology textbook “The Extraction of Hidden Waters” by the 24 Persian mathematician and engineer Karaji. Despite the nature of the understanding and conceptualization of the 25 world by the people of that time, ground-breaking ideas and descriptions of hydrological and hydrogeological 26 perceptions such as components of hydrological cycle, groundwater quality and even driving factors for 27 groundwater flow were presented in the book. Although some of these ideas may have been presented elsewhere, 28 to the best of our knowledge, this is the first time that a whole book was focused on different aspects of hydrology 29 and hydrogeology. More importantly, we are impressed that the book is composed in a way that covered all aspects 30 that are related to an engineering project including technical and construction issues, guidelines for maintenance, 31 and final delivery of the project when the development and construction was over. -

The What and Why of Whole Number Arithmetic: Foundational Ideas from History, Language and Societal Changes
Portland State University PDXScholar Mathematics and Statistics Faculty Fariborz Maseeh Department of Mathematics Publications and Presentations and Statistics 3-2018 The What and Why of Whole Number Arithmetic: Foundational Ideas from History, Language and Societal Changes Xu Hu Sun University of Macau Christine Chambris Université de Cergy-Pontoise Judy Sayers Stockholm University Man Keung Siu University of Hong Kong Jason Cooper Weizmann Institute of Science SeeFollow next this page and for additional additional works authors at: https:/ /pdxscholar.library.pdx.edu/mth_fac Part of the Science and Mathematics Education Commons Let us know how access to this document benefits ou.y Citation Details Sun X.H. et al. (2018) The What and Why of Whole Number Arithmetic: Foundational Ideas from History, Language and Societal Changes. In: Bartolini Bussi M., Sun X. (eds) Building the Foundation: Whole Numbers in the Primary Grades. New ICMI Study Series. Springer, Cham This Book Chapter is brought to you for free and open access. It has been accepted for inclusion in Mathematics and Statistics Faculty Publications and Presentations by an authorized administrator of PDXScholar. Please contact us if we can make this document more accessible: [email protected]. Authors Xu Hu Sun, Christine Chambris, Judy Sayers, Man Keung Siu, Jason Cooper, Jean-Luc Dorier, Sarah Inés González de Lora Sued, Eva Thanheiser, Nadia Azrou, Lynn McGarvey, Catherine Houdement, and Lisser Rye Ejersbo This book chapter is available at PDXScholar: https://pdxscholar.library.pdx.edu/mth_fac/253 Chapter 5 The What and Why of Whole Number Arithmetic: Foundational Ideas from History, Language and Societal Changes Xu Hua Sun , Christine Chambris Judy Sayers, Man Keung Siu, Jason Cooper , Jean-Luc Dorier , Sarah Inés González de Lora Sued , Eva Thanheiser , Nadia Azrou , Lynn McGarvey , Catherine Houdement , and Lisser Rye Ejersbo 5.1 Introduction Mathematics learning and teaching are deeply embedded in history, language and culture (e.g. -

History of Mathematics
Georgia Department of Education History of Mathematics K-12 Mathematics Introduction The Georgia Mathematics Curriculum focuses on actively engaging the students in the development of mathematical understanding by using manipulatives and a variety of representations, working independently and cooperatively to solve problems, estimating and computing efficiently, and conducting investigations and recording findings. There is a shift towards applying mathematical concepts and skills in the context of authentic problems and for the student to understand concepts rather than merely follow a sequence of procedures. In mathematics classrooms, students will learn to think critically in a mathematical way with an understanding that there are many different ways to a solution and sometimes more than one right answer in applied mathematics. Mathematics is the economy of information. The central idea of all mathematics is to discover how knowing some things well, via reasoning, permit students to know much else—without having to commit the information to memory as a separate fact. It is the reasoned, logical connections that make mathematics coherent. The implementation of the Georgia Standards of Excellence in Mathematics places a greater emphasis on sense making, problem solving, reasoning, representation, connections, and communication. History of Mathematics History of Mathematics is a one-semester elective course option for students who have completed AP Calculus or are taking AP Calculus concurrently. It traces the development of major branches of mathematics throughout history, specifically algebra, geometry, number theory, and methods of proofs, how that development was influenced by the needs of various cultures, and how the mathematics in turn influenced culture. The course extends the numbers and counting, algebra, geometry, and data analysis and probability strands from previous courses, and includes a new history strand. -

Can One Design a Geometry Engine? on the (Un) Decidability of Affine
Noname manuscript No. (will be inserted by the editor) Can one design a geometry engine? On the (un)decidability of certain affine Euclidean geometries Johann A. Makowsky Received: June 4, 2018/ Accepted: date Abstract We survey the status of decidabilty of the consequence relation in various ax- iomatizations of Euclidean geometry. We draw attention to a widely overlooked result by Martin Ziegler from 1980, which proves Tarski’s conjecture on the undecidability of finitely axiomatizable theories of fields. We elaborate on how to use Ziegler’s theorem to show that the consequence relations for the first order theory of the Hilbert plane and the Euclidean plane are undecidable. As new results we add: (A) The first order consequence relations for Wu’s orthogonal and metric geometries (Wen- Ts¨un Wu, 1984), and for the axiomatization of Origami geometry (J. Justin 1986, H. Huzita 1991) are undecidable. It was already known that the universal theory of Hilbert planes and Wu’s orthogonal geom- etry is decidable. We show here using elementary model theoretic tools that (B) the universal first order consequences of any geometric theory T of Pappian planes which is consistent with the analytic geometry of the reals is decidable. The techniques used were all known to experts in mathematical logic and geometry in the past but no detailed proofs are easily accessible for practitioners of symbolic computation or automated theorem proving. Keywords Euclidean Geometry · Automated Theorem Proving · Undecidability arXiv:1712.07474v3 [cs.SC] 1 Jun 2018 J.A. Makowsky Faculty of Computer Science, Technion–Israel Institute of Technology, Haifa, Israel E-mail: [email protected] 2 J.A. -

History of Mathematics
History of Mathematics James Tattersall, Providence College (Chair) Janet Beery, University of Redlands Robert E. Bradley, Adelphi University V. Frederick Rickey, United States Military Academy Lawrence Shirley, Towson University Introduction. There are many excellent reasons to study the history of mathematics. It helps students develop a deeper understanding of the mathematics they have already studied by seeing how it was developed over time and in various places. It encourages creative and flexible thinking by allowing students to see historical evidence that there are different and perfectly valid ways to view concepts and to carry out computations. Ideally, a History of Mathematics course should be a part of every mathematics major program. A course taught at the sophomore-level allows mathematics students to see the great wealth of mathematics that lies before them and encourages them to continue studying the subject. A one- or two-semester course taught at the senior level can dig deeper into the history of mathematics, incorporating many ideas from the 19th and 20th centuries that could only be approached with difficulty by less prepared students. Such a senior-level course might be a capstone experience taught in a seminar format. It would be wonderful for students, especially those planning to become middle school or high school mathematics teachers, to have the opportunity to take advantage of both options. We also encourage History of Mathematics courses taught to entering students interested in mathematics, perhaps as First Year or Honors Seminars; to general education students at any level; and to junior and senior mathematics majors and minors. Ideally, mathematics history would be incorporated seamlessly into all courses in the undergraduate mathematics curriculum in addition to being addressed in a few courses of the type we have listed. -

In. ^Ifil Fiegree in PNILOSOPNY
ISLAMIC PHILOSOPHY OF SCIENCE: A CRITICAL STUDY O F HOSSAIN NASR Dis««rtation Submitted TO THE Aiigarh Muslim University, Aligarh for the a^ar d of in. ^Ifil fiegree IN PNILOSOPNY BY SHBIKH ARJBD Abl Under the Kind Supervision of PROF. S. WAHEED AKHTAR Cbiimwa, D«ptt. ol PhiloMphy. DEPARTMENT OF PHILOSOPHY ALIGARH IWIUSLIIM UNIVERSITY ALIGARH 1993 nmiH DS2464 gg®g@eg^^@@@g@@€'@@@@gl| " 0 3 9 H ^ ? S f I O ( D .'^ ••• ¥4 H ,. f f 3« K &^: 3 * 9 m H m «< K t c * - ft .1 D i f m e Q > i j 8"' r E > H I > 5 C I- 115m Vi\ ?- 2 S? 1 i' C £ O H Tl < ACKNOWLEDGEMENT In the name of Allah« the Merciful and the Compassionate. It gives me great pleasure to thanks my kind hearted supervisor Prof. S. Waheed Akhtar, Chairman, Department of Philosophy, who guided me to complete this work. In spite of his multifarious intellectual activities, he gave me valuable time and encouraged me from time to time for this work. Not only he is a philosopher but also a man of literature and sugge'sted me such kind of topic. Without his careful guidance this work could not be completed in proper time. I am indebted to my parents, SK Samser All and Mrs. AJema Khatun and also thankful to my uncle Dr. Sheikh Amjad Ali for encouraging me in research. I am also thankful to my teachers in the department of Philosophy, Dr. M. Rafique, Dr. Tasaduque Hussain, Mr. Naushad, Mr. Muquim and Dr. Sayed. -

Mathematicians Fleeing from Nazi Germany
Mathematicians Fleeing from Nazi Germany Mathematicians Fleeing from Nazi Germany Individual Fates and Global Impact Reinhard Siegmund-Schultze princeton university press princeton and oxford Copyright 2009 © by Princeton University Press Published by Princeton University Press, 41 William Street, Princeton, New Jersey 08540 In the United Kingdom: Princeton University Press, 6 Oxford Street, Woodstock, Oxfordshire OX20 1TW All Rights Reserved Library of Congress Cataloging-in-Publication Data Siegmund-Schultze, R. (Reinhard) Mathematicians fleeing from Nazi Germany: individual fates and global impact / Reinhard Siegmund-Schultze. p. cm. Includes bibliographical references and index. ISBN 978-0-691-12593-0 (cloth) — ISBN 978-0-691-14041-4 (pbk.) 1. Mathematicians—Germany—History—20th century. 2. Mathematicians— United States—History—20th century. 3. Mathematicians—Germany—Biography. 4. Mathematicians—United States—Biography. 5. World War, 1939–1945— Refuges—Germany. 6. Germany—Emigration and immigration—History—1933–1945. 7. Germans—United States—History—20th century. 8. Immigrants—United States—History—20th century. 9. Mathematics—Germany—History—20th century. 10. Mathematics—United States—History—20th century. I. Title. QA27.G4S53 2008 510.09'04—dc22 2008048855 British Library Cataloging-in-Publication Data is available This book has been composed in Sabon Printed on acid-free paper. ∞ press.princeton.edu Printed in the United States of America 10 987654321 Contents List of Figures and Tables xiii Preface xvii Chapter 1 The Terms “German-Speaking Mathematician,” “Forced,” and“Voluntary Emigration” 1 Chapter 2 The Notion of “Mathematician” Plus Quantitative Figures on Persecution 13 Chapter 3 Early Emigration 30 3.1. The Push-Factor 32 3.2. The Pull-Factor 36 3.D. -

Definitions and Nondefinability in Geometry 475 2
Definitions and Nondefinability in Geometry1 James T. Smith Abstract. Around 1900 some noted mathematicians published works developing geometry from its very beginning. They wanted to supplant approaches, based on Euclid’s, which han- dled some basic concepts awkwardly and imprecisely. They would introduce precision re- quired for generalization and application to new, delicate problems in higher mathematics. Their work was controversial: they departed from tradition, criticized standards of rigor, and addressed fundamental questions in philosophy. This paper follows the problem, Which geo- metric concepts are most elementary? It describes a false start, some successful solutions, and an argument that one of those is optimal. It’s about axioms, definitions, and definability, and emphasizes contributions of Mario Pieri (1860–1913) and Alfred Tarski (1901–1983). By fol- lowing this thread of ideas and personalities to the present, the author hopes to kindle interest in a fascinating research area and an exciting era in the history of mathematics. 1. INTRODUCTION. Around 1900 several noted mathematicians published major works on a subject familiar to us from school: developing geometry from the very beginning. They wanted to supplant the established approaches, which were based on Euclid’s, but which handled awkwardly and imprecisely some concepts that Euclid did not treat fully. They would present geometry with the precision required for general- ization and applications to new, delicate problems in higher mathematics—precision beyond the norm for most elementary classes. Work in this area was controversial: these mathematicians departed from tradition, criticized previous standards of rigor, and addressed fundamental questions in logic and philosophy of mathematics.2 After establishing background, this paper tells a story about research into the ques- tion, Which geometric concepts are most elementary? It describes a false start, some successful solutions, and a demonstration that one of those is in a sense optimal. -
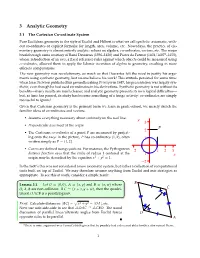
3 Analytic Geometry
3 Analytic Geometry 3.1 The Cartesian Co-ordinate System Pure Euclidean geometry in the style of Euclid and Hilbert is what we call synthetic: axiomatic, with- out co-ordinates or explicit formulæ for length, area, volume, etc. Nowadays, the practice of ele- mentary geometry is almost entirely analytic: reliant on algebra, co-ordinates, vectors, etc. The major breakthrough came courtesy of Rene´ Descartes (1596–1650) and Pierre de Fermat (1601/16071–1655), whose introduction of an axis, a fixed reference ruler against which objects could be measured using co-ordinates, allowed them to apply the Islamic invention of algebra to geometry, resulting in more efficient computations. The new geometry was revolutionary, so much so that Descartes felt the need to justify his argu- ments using synthetic geometry, lest no-one believe his work! This attitude persisted for some time: when Issac Newton published his groundbreaking Principia in 1687, his presentation was largely syn- thetic, even though he had used co-ordinates in his derivations. Synthetic geometry is not without its benefits—many results are much cleaner, and analytic geometry presents its own logical difficulties— but, as time has passed, its study has become something of a fringe activity: co-ordinates are simply too useful to ignore! Given that Cartesian geometry is the primary form we learn in grade-school, we merely sketch the familiar ideas of co-ordinates and vectors. • Assume everything necessary about on the real line. continuity y 3 • Perpendicular axes meet at the origin. P 2 • The Cartesian co-ordinates of a point P are measured by project- ing onto the axes: in the picture, P has co-ordinates (1, 2), often 1 written simply as P = (1, 2).