MOCHI Enables Discovery of Heterogeneous Interactome Modules in 3D Nucleome
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Whole-Genome Microarray Detects Deletions and Loss of Heterozygosity of Chromosome 3 Occurring Exclusively in Metastasizing Uveal Melanoma
Anatomy and Pathology Whole-Genome Microarray Detects Deletions and Loss of Heterozygosity of Chromosome 3 Occurring Exclusively in Metastasizing Uveal Melanoma Sarah L. Lake,1 Sarah E. Coupland,1 Azzam F. G. Taktak,2 and Bertil E. Damato3 PURPOSE. To detect deletions and loss of heterozygosity of disease is fatal in 92% of patients within 2 years of diagnosis. chromosome 3 in a rare subset of fatal, disomy 3 uveal mela- Clinical and histopathologic risk factors for UM metastasis noma (UM), undetectable by fluorescence in situ hybridization include large basal tumor diameter (LBD), ciliary body involve- (FISH). ment, epithelioid cytomorphology, extracellular matrix peri- ϩ ETHODS odic acid-Schiff-positive (PAS ) loops, and high mitotic M . Multiplex ligation-dependent probe amplification 3,4 5 (MLPA) with the P027 UM assay was performed on formalin- count. Prescher et al. showed that a nonrandom genetic fixed, paraffin-embedded (FFPE) whole tumor sections from 19 change, monosomy 3, correlates strongly with metastatic death, and the correlation has since been confirmed by several disomy 3 metastasizing UMs. Whole-genome microarray analy- 3,6–10 ses using a single-nucleotide polymorphism microarray (aSNP) groups. Consequently, fluorescence in situ hybridization were performed on frozen tissue samples from four fatal dis- (FISH) detection of chromosome 3 using a centromeric probe omy 3 metastasizing UMs and three disomy 3 tumors with Ͼ5 became routine practice for UM prognostication; however, 5% years’ metastasis-free survival. to 20% of disomy 3 UM patients unexpectedly develop metas- tases.11 Attempts have therefore been made to identify the RESULTS. Two metastasizing UMs that had been classified as minimal region(s) of deletion on chromosome 3.12–15 Despite disomy 3 by FISH analysis of a small tumor sample were found these studies, little progress has been made in defining the key on MLPA analysis to show monosomy 3. -
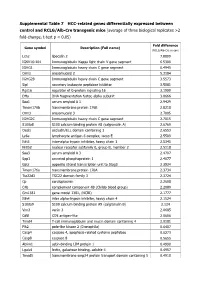
Supplemental Table 7 HCC-Related Genes Differentially Expressed Between Control and RCLG/Alb-Cre Transgenic Mice
Supplemental Table 7 HCC-related genes differentially expressed between control and RCLG/Alb-Cre transgenic mice (average of three biological replicates >2 fold-change, t-test p < 0.05) Fold difference Gene symbol Description (Full name) (RCLG/Alb-Cre vs con) Lcn2 lipocalin 2 7.8899 IGKV16-104 Immunoglobulin Kappa light chain V gene segment 6.5300 IGHG1 Immunoglobulin heavy chain C gene segment 6.4945 Orm2 orosomucoid 2 5.3184 IGHG2B Immunoglobulin heavy chain C gene segment 3.5573 Slpi secretory leukocyte peptidase inhibitor 3.5081 Rgs16 regulator of G-protein signaling 16 3.1999 Dffa DNA fragmentation factor, alpha subunit 3.0666 Saa1 serum amyloid A 1 2.9429 Tmem176b transmembrane protein 176B 2.8218 Orm3 orosomucoid 3 2.7805 IGHG2C Immunoglobulin heavy chain C gene segment 2.7015 S100a8 S100 calcium binding protein A8 (calgranulin A) 2.6769 Ocel1 occludin/ELL domain containing 1 2.6553 Ly6e lymphocyte antigen 6 complex, locus E 2.5509 Itih3 inter-alpha trypsin inhibitor, heavy chain 3 2.5345 Nr0b2 nuclear receptor subfamily 0, group B, member 2 2.5118 Saa3 serum amyloid A 3 2.4707 Spp1 secreted phosphoprotein 1 2.4077 Gats opposite strand transcription unit to Stag3 2.3934 Tmem176a transmembrane protein 176A 2.3734 Tsc22d3 TSC22 domain family 3 2.3724 Cp ceruloplasmin 2.2608 C4b complement component 4B (Childo blood group) 2.2089 Gm1381 gene model 1381, (NCBI) 2.1777 Itih4 inter alpha-trypsin inhibitor, heavy chain 4 2.1524 S100a9 S100 calcium binding protein A9 (calgranulin B) 2.124 Vnn3 vanin 3 2.0685 Cd5l CD5 antigen-like 2.0606 -

4-6 Weeks Old Female C57BL/6 Mice Obtained from Jackson Labs Were Used for Cell Isolation
Methods Mice: 4-6 weeks old female C57BL/6 mice obtained from Jackson labs were used for cell isolation. Female Foxp3-IRES-GFP reporter mice (1), backcrossed to B6/C57 background for 10 generations, were used for the isolation of naïve CD4 and naïve CD8 cells for the RNAseq experiments. The mice were housed in pathogen-free animal facility in the La Jolla Institute for Allergy and Immunology and were used according to protocols approved by the Institutional Animal Care and use Committee. Preparation of cells: Subsets of thymocytes were isolated by cell sorting as previously described (2), after cell surface staining using CD4 (GK1.5), CD8 (53-6.7), CD3ε (145- 2C11), CD24 (M1/69) (all from Biolegend). DP cells: CD4+CD8 int/hi; CD4 SP cells: CD4CD3 hi, CD24 int/lo; CD8 SP cells: CD8 int/hi CD4 CD3 hi, CD24 int/lo (Fig S2). Peripheral subsets were isolated after pooling spleen and lymph nodes. T cells were enriched by negative isolation using Dynabeads (Dynabeads untouched mouse T cells, 11413D, Invitrogen). After surface staining for CD4 (GK1.5), CD8 (53-6.7), CD62L (MEL-14), CD25 (PC61) and CD44 (IM7), naïve CD4+CD62L hiCD25-CD44lo and naïve CD8+CD62L hiCD25-CD44lo were obtained by sorting (BD FACS Aria). Additionally, for the RNAseq experiments, CD4 and CD8 naïve cells were isolated by sorting T cells from the Foxp3- IRES-GFP mice: CD4+CD62LhiCD25–CD44lo GFP(FOXP3)– and CD8+CD62LhiCD25– CD44lo GFP(FOXP3)– (antibodies were from Biolegend). In some cases, naïve CD4 cells were cultured in vitro under Th1 or Th2 polarizing conditions (3, 4). -

Alterations of Genetic Variants and Transcriptomic Features of Response to Tamoxifen in the Breast Cancer Cell Line
Alterations of Genetic Variants and Transcriptomic Features of Response to Tamoxifen in the Breast Cancer Cell Line Mahnaz Nezamivand-Chegini Shiraz University Hamed Kharrati-Koopaee Shiraz University https://orcid.org/0000-0003-2345-6919 seyed taghi Heydari ( [email protected] ) Shiraz University of Medical Sciences https://orcid.org/0000-0001-7711-1137 Hasan Giahi Shiraz University Ali Dehshahri Shiraz University of Medical Sciences Mehdi Dianatpour Shiraz University of Medical Sciences Kamran Bagheri Lankarani Shiraz University of Medical Sciences Research Keywords: Tamoxifen, breast cancer, genetic variants, RNA-seq. Posted Date: August 17th, 2021 DOI: https://doi.org/10.21203/rs.3.rs-783422/v1 License: This work is licensed under a Creative Commons Attribution 4.0 International License. Read Full License Page 1/33 Abstract Background Breast cancer is one of the most important causes of mortality in the world, and Tamoxifen therapy is known as a medication strategy for estrogen receptor-positive breast cancer. In current study, two hypotheses of Tamoxifen consumption in breast cancer cell line (MCF7) were investigated. First, the effect of Tamoxifen on genes expression prole at transcriptome level was evaluated between the control and treated samples. Second, due to the fact that Tamoxifen is known as a mutagenic factor, there may be an association between the alterations of genetic variants and Tamoxifen treatment, which can impact on the drug response. Methods In current study, the whole-transcriptome (RNA-seq) dataset of four investigations (19 samples) were derived from European Bioinformatics Institute (EBI). At transcriptome level, the effect of Tamoxifen was investigated on gene expression prole between control and treatment samples. -

Supplemental Information
Supplemental information Dissection of the genomic structure of the miR-183/96/182 gene. Previously, we showed that the miR-183/96/182 cluster is an intergenic miRNA cluster, located in a ~60-kb interval between the genes encoding nuclear respiratory factor-1 (Nrf1) and ubiquitin-conjugating enzyme E2H (Ube2h) on mouse chr6qA3.3 (1). To start to uncover the genomic structure of the miR- 183/96/182 gene, we first studied genomic features around miR-183/96/182 in the UCSC genome browser (http://genome.UCSC.edu/), and identified two CpG islands 3.4-6.5 kb 5’ of pre-miR-183, the most 5’ miRNA of the cluster (Fig. 1A; Fig. S1 and Seq. S1). A cDNA clone, AK044220, located at 3.2-4.6 kb 5’ to pre-miR-183, encompasses the second CpG island (Fig. 1A; Fig. S1). We hypothesized that this cDNA clone was derived from 5’ exon(s) of the primary transcript of the miR-183/96/182 gene, as CpG islands are often associated with promoters (2). Supporting this hypothesis, multiple expressed sequences detected by gene-trap clones, including clone D016D06 (3, 4), were co-localized with the cDNA clone AK044220 (Fig. 1A; Fig. S1). Clone D016D06, deposited by the German GeneTrap Consortium (GGTC) (http://tikus.gsf.de) (3, 4), was derived from insertion of a retroviral construct, rFlpROSAβgeo in 129S2 ES cells (Fig. 1A and C). The rFlpROSAβgeo construct carries a promoterless reporter gene, the β−geo cassette - an in-frame fusion of the β-galactosidase and neomycin resistance (Neor) gene (5), with a splicing acceptor (SA) immediately upstream, and a polyA signal downstream of the β−geo cassette (Fig. -

Supplementary Table S4. FGA Co-Expressed Gene List in LUAD
Supplementary Table S4. FGA co-expressed gene list in LUAD tumors Symbol R Locus Description FGG 0.919 4q28 fibrinogen gamma chain FGL1 0.635 8p22 fibrinogen-like 1 SLC7A2 0.536 8p22 solute carrier family 7 (cationic amino acid transporter, y+ system), member 2 DUSP4 0.521 8p12-p11 dual specificity phosphatase 4 HAL 0.51 12q22-q24.1histidine ammonia-lyase PDE4D 0.499 5q12 phosphodiesterase 4D, cAMP-specific FURIN 0.497 15q26.1 furin (paired basic amino acid cleaving enzyme) CPS1 0.49 2q35 carbamoyl-phosphate synthase 1, mitochondrial TESC 0.478 12q24.22 tescalcin INHA 0.465 2q35 inhibin, alpha S100P 0.461 4p16 S100 calcium binding protein P VPS37A 0.447 8p22 vacuolar protein sorting 37 homolog A (S. cerevisiae) SLC16A14 0.447 2q36.3 solute carrier family 16, member 14 PPARGC1A 0.443 4p15.1 peroxisome proliferator-activated receptor gamma, coactivator 1 alpha SIK1 0.435 21q22.3 salt-inducible kinase 1 IRS2 0.434 13q34 insulin receptor substrate 2 RND1 0.433 12q12 Rho family GTPase 1 HGD 0.433 3q13.33 homogentisate 1,2-dioxygenase PTP4A1 0.432 6q12 protein tyrosine phosphatase type IVA, member 1 C8orf4 0.428 8p11.2 chromosome 8 open reading frame 4 DDC 0.427 7p12.2 dopa decarboxylase (aromatic L-amino acid decarboxylase) TACC2 0.427 10q26 transforming, acidic coiled-coil containing protein 2 MUC13 0.422 3q21.2 mucin 13, cell surface associated C5 0.412 9q33-q34 complement component 5 NR4A2 0.412 2q22-q23 nuclear receptor subfamily 4, group A, member 2 EYS 0.411 6q12 eyes shut homolog (Drosophila) GPX2 0.406 14q24.1 glutathione peroxidase -

Structural Insights Into the Architecture and Membrane Interactions of the Conserved COMMD Proteins
RESEARCH ARTICLE Structural insights into the architecture and membrane interactions of the conserved COMMD proteins Michael D Healy1, Manuela K Hospenthal2†, Ryan J Hall1, Mintu Chandra1, Molly Chilton3, Vikas Tillu1, Kai-En Chen1, Dion J Celligoi2, Fiona J McDonald4, Peter J Cullen3, J Shaun Lott2, Brett M Collins1*, Rajesh Ghai1* 1Institute for Molecular Bioscience, The University of Queensland, St. Lucia, Australia; 2School of Biological Sciences, The University of Auckland, Auckland, New Zealand; 3School of Biochemistry, Biomedical Sciences Building, University of Bristol, Bristol, United Kingdom; 4Department of Physiology, University of Otago, Dunedin, New Zealand Abstract The COMMD proteins are a conserved family of proteins with central roles in intracellular membrane trafficking and transcription. They form oligomeric complexes with each other and act as components of a larger assembly called the CCC complex, which is localized to endosomal compartments and mediates the transport of several transmembrane cargos. How these complexes are formed however is completely unknown. Here, we have systematically characterised the interactions between human COMMD proteins, and determined structures of *For correspondence: [email protected] (BMC); COMMD proteins using X-ray crystallography and X-ray scattering to provide insights into the [email protected] (RG) underlying mechanisms of homo- and heteromeric assembly. All COMMD proteins possess an a- helical N-terminal domain, and a highly conserved C-terminal domain that forms a tightly † Present address: Institute of interlocked dimeric structure responsible for COMMD-COMMD interactions. The COMM domains Structural and Molecular Biology, also bind directly to components of CCC and mediate non-specific membrane association. Overall Department of Biological these studies show that COMMD proteins function as obligatory dimers with conserved domain Sciences, Birkbeck College, London, United Kingdom architectures. -

A Chromosome Level Genome of Astyanax Mexicanus Surface Fish for Comparing Population
bioRxiv preprint doi: https://doi.org/10.1101/2020.07.06.189654; this version posted July 6, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. 1 Title 2 A chromosome level genome of Astyanax mexicanus surface fish for comparing population- 3 specific genetic differences contributing to trait evolution. 4 5 Authors 6 Wesley C. Warren1, Tyler E. Boggs2, Richard Borowsky3, Brian M. Carlson4, Estephany 7 Ferrufino5, Joshua B. Gross2, LaDeana Hillier6, Zhilian Hu7, Alex C. Keene8, Alexander Kenzior9, 8 Johanna E. Kowalko5, Chad Tomlinson10, Milinn Kremitzki10, Madeleine E. Lemieux11, Tina 9 Graves-Lindsay10, Suzanne E. McGaugh12, Jeff T. Miller12, Mathilda Mommersteeg7, Rachel L. 10 Moran12, Robert Peuß9, Edward Rice1, Misty R. Riddle13, Itzel Sifuentes-Romero5, Bethany A. 11 Stanhope5,8, Clifford J. Tabin13, Sunishka Thakur5, Yamamoto Yoshiyuki14, Nicolas Rohner9,15 12 13 Authors for correspondence: Wesley C. Warren ([email protected]), Nicolas Rohner 14 ([email protected]) 15 16 Affiliation 17 1Department of Animal Sciences, Department of Surgery, Institute for Data Science and 18 Informatics, University of Missouri, Bond Life Sciences Center, Columbia, MO 19 2 Department of Biological Sciences, University of Cincinnati, Cincinnati, OH 20 3 Department of Biology, New York University, New York, NY 21 4 Department of Biology, The College of Wooster, Wooster, OH 22 5 Harriet L. Wilkes Honors College, Florida Atlantic University, Jupiter FL 23 6 Department of Genome Sciences, University of Washington, Seattle, WA 1 bioRxiv preprint doi: https://doi.org/10.1101/2020.07.06.189654; this version posted July 6, 2020. -

Role and Regulation of the P53-Homolog P73 in the Transformation of Normal Human Fibroblasts
Role and regulation of the p53-homolog p73 in the transformation of normal human fibroblasts Dissertation zur Erlangung des naturwissenschaftlichen Doktorgrades der Bayerischen Julius-Maximilians-Universität Würzburg vorgelegt von Lars Hofmann aus Aschaffenburg Würzburg 2007 Eingereicht am Mitglieder der Promotionskommission: Vorsitzender: Prof. Dr. Dr. Martin J. Müller Gutachter: Prof. Dr. Michael P. Schön Gutachter : Prof. Dr. Georg Krohne Tag des Promotionskolloquiums: Doktorurkunde ausgehändigt am Erklärung Hiermit erkläre ich, dass ich die vorliegende Arbeit selbständig angefertigt und keine anderen als die angegebenen Hilfsmittel und Quellen verwendet habe. Diese Arbeit wurde weder in gleicher noch in ähnlicher Form in einem anderen Prüfungsverfahren vorgelegt. Ich habe früher, außer den mit dem Zulassungsgesuch urkundlichen Graden, keine weiteren akademischen Grade erworben und zu erwerben gesucht. Würzburg, Lars Hofmann Content SUMMARY ................................................................................................................ IV ZUSAMMENFASSUNG ............................................................................................. V 1. INTRODUCTION ................................................................................................. 1 1.1. Molecular basics of cancer .......................................................................................... 1 1.2. Early research on tumorigenesis ................................................................................. 3 1.3. Developing -

The Roles of RNA Polymerase I and III Subunits Polr1a, Polr1c, and Polr1d in Craniofacial Development BY
The roles of RNA Polymerase I and III subunits Polr1a, Polr1c, and Polr1d in craniofacial development BY © 2016 Kristin Emily Noack Watt Submitted to the graduate degree program in Anatomy and Cell Biology and to the Graduate Faculty of The University of Kansas Medical Center in partial fulfillment of the requirements for the degree of Doctor of Philosophy. Paul Trainor, Co-Chairperson Brenda Rongish, Co-Chairperson Brian Andrews Jennifer Gerton Tatjana Piotrowski Russell Swerdlow Date Defended: January 26, 2016 The Dissertation Committee for Kristin Watt certifies that this is the approved version of the following dissertation: The roles of RNA Polymerase I and III subunits Polr1a, Polr1c, and Polr1d in craniofacial development Paul Trainor, Co-Chairperson Brenda Rongish, Co-Chairperson Date approved: February 2, 2016 ii Abstract Craniofacial anomalies account for approximately one-third of all birth defects. Two examples of syndromes associated with craniofacial malformations are Treacher Collins syndrome and Acrofacial Dysostosis, Cincinnati type which have phenotypic overlap including deformities of the eyes, ears, and facial bones. Mutations in TCOF1, POLR1C or POLR1D may cause Treacher Collins syndrome while mutations in POLR1A may cause Acrofacial Dysostosis, Cincinnati type. TCOF1 encodes the nucleolar phosphoprotein Treacle, which functions in rRNA transcription and modification. Previous studies demonstrated that Tcof1 mutations in mice result in reduced ribosome biogenesis and increased neuroepithelial apoptosis. This diminishes the neural crest cell (NCC) progenitor population which contribute to the development of the cranial skeleton. In contrast, apart from being subunits of RNA Polymerases (RNAP) I and/or III, nothing is known about the function of POLR1A, POLR1C, and POLR1D during embryonic and craniofacial development. -

MOCHI Enables Discovery of Heterogeneous Interactome Modules in 3D Nucleome
Downloaded from genome.cshlp.org on October 4, 2021 - Published by Cold Spring Harbor Laboratory Press MOCHI enables discovery of heterogeneous interactome modules in 3D nucleome Dechao Tian1,# , Ruochi Zhang1,# , Yang Zhang1, Xiaopeng Zhu1, and Jian Ma1,* 1Computational Biology Department, School of Computer Science, Carnegie Mellon University, Pittsburgh, PA 15213, USA #These two authors contributed equally *Correspondence: [email protected] Contact To whom correspondence should be addressed: Jian Ma School of Computer Science Carnegie Mellon University 7705 Gates-Hillman Complex 5000 Forbes Avenue Pittsburgh, PA 15213 Phone: +1 (412) 268-2776 Email: [email protected] 1 Downloaded from genome.cshlp.org on October 4, 2021 - Published by Cold Spring Harbor Laboratory Press Abstract The composition of the cell nucleus is highly heterogeneous, with different constituents forming complex interactomes. However, the global patterns of these interwoven heterogeneous interactomes remain poorly understood. Here we focus on two different interactomes, chromatin interaction network and gene regulatory network, as a proof-of-principle, to identify heterogeneous interactome modules (HIMs), each of which represents a cluster of gene loci that are in spatial contact more frequently than expected and that are regulated by the same group of transcription factors. HIM integrates transcription factor binding and 3D genome structure to reflect “transcriptional niche” in the nucleus. We develop a new algorithm MOCHI to facilitate the discovery of HIMs based on network motif clustering in heterogeneous interactomes. By applying MOCHI to five different cell types, we found that HIMs have strong spatial preference within the nucleus and exhibit distinct functional properties. Through integrative analysis, this work demonstrates the utility of MOCHI to identify HIMs, which may provide new perspectives on the interplay between transcriptional regulation and 3D genome organization. -

Human Induced Pluripotent Stem Cell–Derived Podocytes Mature Into Vascularized Glomeruli Upon Experimental Transplantation
BASIC RESEARCH www.jasn.org Human Induced Pluripotent Stem Cell–Derived Podocytes Mature into Vascularized Glomeruli upon Experimental Transplantation † Sazia Sharmin,* Atsuhiro Taguchi,* Yusuke Kaku,* Yasuhiro Yoshimura,* Tomoko Ohmori,* ‡ † ‡ Tetsushi Sakuma, Masashi Mukoyama, Takashi Yamamoto, Hidetake Kurihara,§ and | Ryuichi Nishinakamura* *Department of Kidney Development, Institute of Molecular Embryology and Genetics, and †Department of Nephrology, Faculty of Life Sciences, Kumamoto University, Kumamoto, Japan; ‡Department of Mathematical and Life Sciences, Graduate School of Science, Hiroshima University, Hiroshima, Japan; §Division of Anatomy, Juntendo University School of Medicine, Tokyo, Japan; and |Japan Science and Technology Agency, CREST, Kumamoto, Japan ABSTRACT Glomerular podocytes express proteins, such as nephrin, that constitute the slit diaphragm, thereby contributing to the filtration process in the kidney. Glomerular development has been analyzed mainly in mice, whereas analysis of human kidney development has been minimal because of limited access to embryonic kidneys. We previously reported the induction of three-dimensional primordial glomeruli from human induced pluripotent stem (iPS) cells. Here, using transcription activator–like effector nuclease-mediated homologous recombination, we generated human iPS cell lines that express green fluorescent protein (GFP) in the NPHS1 locus, which encodes nephrin, and we show that GFP expression facilitated accurate visualization of nephrin-positive podocyte formation in