DOCSLIB.ORG

Topic 3 the Δ-Function & Convolution. Impulse Response & Transfer Function

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Topic 3 the Δ-Function & Convolution. Impulse Response & Transfer Function Topic 3 The δ-function & convolution. Impulse response & Transfer function In this lecture we will described the mathematic operation of the convolution of two continuous functions. As the name suggests, two functions are blended or folded together. We will then discuss the impulse response of a system, and show how it is related to the transfer function of the system. First though we will define a special function called the δ-function or unit impulse. It is, like the Heaviside step function u(t), a generalized function or \distribution" and is best defined by considering another function in conjunction with it. 3.1 The δ-function Consider a function 1=w 0 < t < w g(t) = 0 otherwise One thing of note about g(t) is that Z w g(t)dt = 1: 0− The lower limit 0− is a infinitesimally small amount less than zero. Now, suppose that the width w gets very small, indeed as small at 0+, an number an infinitesimal amount bigger than zero. At that point, g(t) has become like the δ function, a very thin, very high spike at zero, such that Z 1 Z 0+ δ(t)dt = δ(t)dt = 1 −∞ 0− 1 3/2 g(t) δ (t) 1/ w 0 w 0 (a) (b) Figure 3.1: As w becomes very small the function g(t) turns into a δ-function δ(t) indicated by the arrowed spike. In some sense it is akin to the derivative of the Heaviside unit step Z t δ(t)dt = u(t) : −∞ More formally the delta function is defined in association with any arbitrary function f (t), as The delta function ... Z 1 f (t)δ(t)dt = f (0) : −∞ Picking out values of a function in this way is called sifting of f (t) by δ(t). We can also see that Z 1 f (t)δ(t − τ)dt = f (τ) ; −∞ a result that we will return to. δ (t−τ ) A δ (t−τ ) δ f(t) (t) f(t) t t 0 0 τ 0 τ (a) (b) (c) Figure 3.2: (a,b) Sifting. (c) With an amplitude A. Although the δ-function is infinitely high, very often you will see a described as the unit δ-function, or see a δ-function spike with an amplitude A by it. This is to R 1 R 1 denote a delta-function where −∞ δ(t)dt = 1 or −∞ Aδ(t)dt = A. 3/3 3.2 Properties of the δ-function Fourier transform of the delta function: FT [δ(t)] = 1 Proof: Use the definition of the δ-function and sift the function f (t) = e−i!t: Z 1 δ(t)e−i!tdt = e−i!0 = 1 : −∞ Symmetry: The δ-function has even symmetry. δ(t) = δ(−t) Parameter Scaling: 1 δ(at) = δ(t) jaj R 1 Proof: To prove this return to the fundamental definition, −∞ f (t)δ(t)dt = f (0) If a ≥ 0, substitute (at) for t (no swap in limits) Z 1 Z 1 f (at)δ(at)d(at) = a f (at)δ(at)dt = f (0) −∞ −∞ Z 1 But f (at)δ(t)dt = f (0) ) a δ(at) = δ(t): −∞ Now if a < 0, substitute (at) for t (but need to swap limits as a negative) Z −∞ Z 1 f (at)δ(at)d(at) = − a f (at)δ(at)dt = f (0) 1 −∞ Z 1 But f (at)δ(t)dt = f (0) ) −a δ(at) = δ(t): −∞ So jaj δ(at) = δ(t) covers both cases, and the stated definition follows immedi- ately. 3/4 3.3 Fourier Transforms that involve the δ-function Fourier Transform of ei!0t Z 1 i!0t i(!0−!)t FT e = e dt = 2πδ(! − !0) : −∞ Fourier Transform of 1 FT [1] = 2πδ(!) : You could obtain this either by putting !0 = 0 just above, or by using the dual property, FT [1] = 2πδ(−!), then the even symmetry property δ(−!) = δ(!). Fourier Transform of cos !0t 1 FT [cos ! t] = FT ei!0t + e−i!0t = π (δ(! − ! ) + δ(! + ! )) : 0 2 0 0 Fourier Transform of sin !0t 1 FT [cos ! t] = FT ei!0t − e−i!0t = −iπ (δ(! − ! ) − δ(! + ! )) : 0 2i 0 0 Fourier Transform of Complex Fourier Series | yes, this can be useful! " n=1 # n=1 X in!0t X FT Cne = 2π Cnδ(! − n!0) : n=−∞ n=−∞ 3.4 Convolution We turn now to a very important technique is signal analysis and processing. The convolution of two functions f (t) and g(t) is denoted by f ∗ g. The convolution is defined by an integral over the dummy variable τ. The convolution integral. The value of f ∗ g at t is Z 1 (f ∗ g)(t) = f (τ)g(t − τ)dτ −∞ 3/5 The process is commutative, which means that Z 1 Z 1 (f ∗ g)(t) ≡ (g ∗ f )(t) or f (τ)g(t − τ)dτ ≡ f (t − τ)g(τ)dτ −∞ −∞ 3.4.1 | Example 1 It is easier to \see" what is going on when convolving a signal f with a function g of even or odd symmetry. However, to get into a strict routine, it is best to start with an example with no symmetry. [Q] Find and sketch the convolution of f (t) = u(t)e−at with g(t) = u(t)e−bt, where both a and b are positive. [A] Using the first form of the convolution integral, the \short" answer must be the unintelligible Z 1 f ∗ g = u(τ)e−aτ u(t − τ)e−b(t−τ)dτ : −∞ First, make sketches of the functions f (τ) and g(t −τ) as τ varies. Function f (τ) looks just like f (t) of course. But g(t − τ) is a reflected (\time reversed") and shifted version of g(t). (The reflection is easy enough. To check that the shift is correct, ask yourself \where does the function g(p) drop?" The answer is at p = 0. So g(t − τ) must drop when t − τ = 0, that is when τ = t.) f(τ ) g(τ ) g(−τ ) g(t−τ ) τ τ τ τ 0 0 t 0 ! ! 0 (a) (b) ! (c) ! (d) Figure 3.3: We now multiply the two functions, BUT we must worry about the fact that t is a variable. In this case there are two different regimes, one when t < 0 and the other when t ≥ 0. Figure 3.4 shows the result. So now to the integration. For t < 0, the function on the bottom left of Figure 3.4 is everywhere zero, and the result is zero. For t ≥ 0 Z 1 Z t e−bt u(τ)e−aτ u(t−τ)e−b(t−τ)dτ = e−bt e(b−a)τ dτ = e(b−a)t − 1 −∞ 0 b − a 3/6 g(t−τ ) f(τ ) g(t−τ ) f(τ ) τ τ t 0 0 t f(τ )g(t−τ ) f(τ )g(t−τ ) t <0 t >0 τ τ 0 t 0 t Figure 3.4: So e−at − e−bt =(b − a) for t ≥ 0 f ∗ g(t) = 0 for t < 0 It is important to realize that the function at the bottom right of Figure 3.4 is NOT the convolution. That is the function you are about to integrate over for a particular value of t. Figure 3.5 shows the t > 0 part of the convolution for b = 2 and a = 1. 0.25 (exp(-x)-exp(-2*x)) 0.2 0.15 0.1 0.05 0 0 1 2 3 4 5 6 Figure 3.5: f ∗ g(t) plotted for t > 0 when b = 2 and a = 1. 3/7 3.4.2 | Example 2 [Q] Derive an expression for the convolution of an arbitrary signal f (t) with the function g(t) shown in the figure. Determine the convolution when f (t) = A, a constant, and when f (t) = A + (B − A)u(t). [A] Follow the routine. Function f (τ) looks exactly like f (t), but g(t − τ) is reflected and shifted. Multiply and integrate over τ from −∞ to 1. Because g only has finite range, we can pinch in the limits of integration, and the convolution becomes Z t Z t+a f ∗ g = − f (τ)dτ + f (τ)dτ t−a t g(t) f(t) g(t− τ ) f(t) 1 a t 1 −a t t−a t τ −1 t t+a −1 Figure 3.6: When f (t) = A, a constant, it is obvious by inspection that the convolution is zero for all t. When f (t) = A + (B − A)u(t), we have to be more careful because there is a discontinuity in the function. From Figure 3.7(a): • The convolution is zero for all t < −a and all t > a (Diagram positions 1,2,5). • The maximum value is when t = 0 (Position 4). By inspection, or using the integrals above, (f ∗ g)(t = 0) = a(B − A). • For −a < t < 0, (Position 3) Z t Z 0 Z t+a f ∗g = − (A)dτ+ Adτ+ Bdτ = −aA+−tA+(t+a)B = (a+t)(B−A) t−a t 0 showing that the increase in correlation value is linear. Symmetry tells us that the decrease for 0 < t < a will also be linear. One can see from Figure 3.7(b) that this convolution provides a rudimentary de- tector of steps in the signal.
Load more

Recommended publications
  • J-DSP Lab 2: the Z-Transform and Frequency Responses
    J-DSP Lab 2: The Z-Transform and Frequency Responses Introduction This lab exercise will cover the Z transform and the frequency response of digital filters. The goal of this exercise is to familiarize you with the utility of the Z transform in digital signal processing. The Z transform has a similar role in DSP as the Laplace transform has in circuit analysis: a) It provides intuition in certain cases, e.g., pole location and filter stability, b) It facilitates compact signal representations, e.g., certain deterministic infinite-length sequences can be represented by compact rational z-domain functions, c) It allows us to compute signal outputs in source-system configurations in closed form, e.g., using partial functions to compute transient and steady state responses. d) It associates intuitively with frequency domain representations and the Fourier transform In this lab we use the Filter block of J-DSP to invert the Z transform of various signals. As we have seen in the previous lab, the Filter block in J-DSP can implement a filter transfer function of the following form 10 −i ∑bi z i=0 H (z) = 10 − j 1+ ∑ a j z j=1 This is essentially realized as an I/P-O/P difference equation of the form L M y(n) = ∑∑bi x(n − i) − ai y(n − i) i==01i The transfer function is associated with the impulse response and hence the output can also be written as y(n) = x(n) * h(n) Here, * denotes convolution; x(n) and y(n) are the input signal and output signal respectively.
    [Show full text]
  • Lecture 3: Transfer Function and Dynamic Response Analysis
    Transfer function approach Dynamic response Summary Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis Paweł Malczyk Division of Theory of Machines and Robots Institute of Aeronautics and Applied Mechanics Faculty of Power and Aeronautical Engineering Warsaw University of Technology October 17, 2019 © Paweł Malczyk. Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis 1 / 31 Transfer function approach Dynamic response Summary Outline 1 Transfer function approach 2 Dynamic response 3 Summary © Paweł Malczyk. Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis 2 / 31 Transfer function approach Dynamic response Summary Transfer function approach 1 Transfer function approach SISO system Definition Poles and zeros Transfer function for multivariable system Properties 2 Dynamic response 3 Summary © Paweł Malczyk. Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis 3 / 31 Transfer function approach Dynamic response Summary SISO system Fig. 1: Block diagram of a single input single output (SISO) system Consider the continuous, linear time-invariant (LTI) system defined by linear constant coefficient ordinary differential equation (LCCODE): dny dn−1y + − + ··· + _ + = an n an 1 n−1 a1y a0y dt dt (1) dmu dm−1u = b + b − + ··· + b u_ + b u m dtm m 1 dtm−1 1 0 initial conditions y(0), y_(0),..., y(n−1)(0), and u(0),..., u(m−1)(0) given, u(t) – input signal, y(t) – output signal, ai – real constants for i = 1, ··· , n, and bj – real constants for j = 1, ··· , m. How do I find the LCCODE (1)? .
    [Show full text]
  • GENERALIZED FUNCTIONS LECTURES Contents 1. the Space
    GENERALIZED FUNCTIONS LECTURES Contents 1. The space of generalized functions on Rn 2 1.1. Motivation 2 1.2. Basic definitions 3 1.3. Derivatives of generalized functions 5 1.4. The support of generalized functions 6 1.5. Products and convolutions of generalized functions 7 1.6. Generalized functions on Rn 8 1.7. Generalized functions and differential operators 9 1.8. Regularization of generalized functions 9 n 2. Topological properties of Cc∞(R ) 11 2.1. Normed spaces 11 2.2. Topological vector spaces 12 2.3. Defining completeness 14 2.4. Fréchet spaces 15 2.5. Sequence spaces 17 2.6. Direct limits of Fréchet spaces 18 2.7. Topologies on the space of distributions 19 n 3. Geometric properties of C−∞(R ) 21 3.1. Sheaf of distributions 21 3.2. Filtration on spaces of distributions 23 3.3. Functions and distributions on a Cartesian product 24 4. p-adic numbers and `-spaces 26 4.1. Defining p-adic numbers 26 4.2. Misc. -not sure what to do with them (add to an appendix about p-adic numbers?) 29 4.3. p-adic expansions 31 4.4. Inverse limits 32 4.5. Haar measure and local fields 32 4.6. Some basic properties of `-spaces. 33 4.7. Distributions on `-spaces 35 4.8. Distributions supported on a subspace 35 5. Vector valued distributions 37 Date: October 7, 2018. 1 GENERALIZED FUNCTIONS LECTURES 2 5.1. Smooth measures 37 5.2. Generalized functions versus distributions 38 5.3. Some linear algebra 39 5.4. Generalized functions supported on a subspace 41 6.
    [Show full text]
  • Control Theory
    Control theory S. Simrock DESY, Hamburg, Germany Abstract In engineering and mathematics, control theory deals with the behaviour of dynamical systems. The desired output of a system is called the reference. When one or more output variables of a system need to follow a certain ref- erence over time, a controller manipulates the inputs to a system to obtain the desired effect on the output of the system. Rapid advances in digital system technology have radically altered the control design options. It has become routinely practicable to design very complicated digital controllers and to carry out the extensive calculations required for their design. These advances in im- plementation and design capability can be obtained at low cost because of the widespread availability of inexpensive and powerful digital processing plat- forms and high-speed analog IO devices. 1 Introduction The emphasis of this tutorial on control theory is on the design of digital controls to achieve good dy- namic response and small errors while using signals that are sampled in time and quantized in amplitude. Both transform (classical control) and state-space (modern control) methods are described and applied to illustrative examples. The transform methods emphasized are the root-locus method of Evans and fre- quency response. The state-space methods developed are the technique of pole assignment augmented by an estimator (observer) and optimal quadratic-loss control. The optimal control problems use the steady-state constant gain solution. Other topics covered are system identification and non-linear control. System identification is a general term to describe mathematical tools and algorithms that build dynamical models from measured data.
    [Show full text]
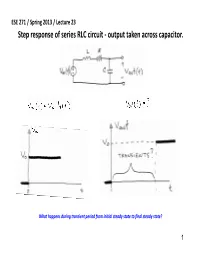
  • Step Response of Series RLC Circuit ‐ Output Taken Across Capacitor
    ESE 271 / Spring 2013 / Lecture 23 Step response of series RLC circuit ‐ output taken across capacitor. What happens during transient period from initial steady state to final steady state? 1 ESE 271 / Spring 2013 / Lecture 23 Transfer function of series RLC ‐ output taken across capacitor. Poles: Case 1: ‐‐two differen t real poles Case 2: ‐ two identical real poles ‐ complex conjugate poles Case 3: 2 ESE 271 / Spring 2013 / Lecture 23 Case 1: two different real poles. Step response of series RLC ‐ output taken across capacitor. Overdamped case –the circuit demonstrates relatively slow transient response. 3 ESE 271 / Spring 2013 / Lecture 23 Case 1: two different real poles. Freqqyuency response of series RLC ‐ output taken across capacitor. Uncorrected Bode Gain Plot Overdamped case –the circuit demonstrates relatively limited bandwidth 4 ESE 271 / Spring 2013 / Lecture 23 Case 2: two identical real poles. Step response of series RLC ‐ output taken across capacitor. Critically damped case –the circuit demonstrates the shortest possible rise time without overshoot. 5 ESE 271 / Spring 2013 / Lecture 23 Case 2: two identical real poles. Freqqyuency response of series RLC ‐ output taken across capacitor. Critically damped case –the circuit demonstrates the widest bandwidth without apparent resonance. Uncorrected Bode Gain Plot 6 ESE 271 / Spring 2013 / Lecture 23 Case 3: two complex poles. Step response of series RLC ‐ output taken across capacitor. Underdamped case – the circuit oscillates. 7 ESE 271 / Spring 2013 / Lecture 23 Case 3: two complex poles. Freqqyuency response of series RLC ‐ output taken across capacitor. Corrected Bode GiGain Plot Underdamped case –the circuit can demonstrate apparent resonant behavior.
    [Show full text]
  • Frequency Response and Bode Plots
    1 Frequency Response and Bode Plots 1.1 Preliminaries The steady-state sinusoidal frequency-response of a circuit is described by the phasor transfer function Hj( ) . A Bode plot is a graph of the magnitude (in dB) or phase of the transfer function versus frequency. Of course we can easily program the transfer function into a computer to make such plots, and for very complicated transfer functions this may be our only recourse. But in many cases the key features of the plot can be quickly sketched by hand using some simple rules that identify the impact of the poles and zeroes in shaping the frequency response. The advantage of this approach is the insight it provides on how the circuit elements influence the frequency response. This is especially important in the design of frequency-selective circuits. We will first consider how to generate Bode plots for simple poles, and then discuss how to handle the general second-order response. Before doing this, however, it may be helpful to review some properties of transfer functions, the decibel scale, and properties of the log function. Poles, Zeroes, and Stability The s-domain transfer function is always a rational polynomial function of the form Ns() smm as12 a s m asa Hs() K K mm12 10 (1.1) nn12 n Ds() s bsnn12 b s bsb 10 As we have seen already, the polynomials in the numerator and denominator are factored to find the poles and zeroes; these are the values of s that make the numerator or denominator zero. If we write the zeroes as zz123,, zetc., and similarly write the poles as pp123,, p , then Hs( ) can be written in factored form as ()()()s zsz sz Hs() K 12 m (1.2) ()()()s psp12 sp n 1 © Bob York 2009 2 Frequency Response and Bode Plots The pole and zero locations can be real or complex.
    [Show full text]
  • The Scientist and Engineer's Guide to Digital Signal Processing Properties of Convolution
    CHAPTER 7 Properties of Convolution A linear system's characteristics are completely specified by the system's impulse response, as governed by the mathematics of convolution. This is the basis of many signal processing techniques. For example: Digital filters are created by designing an appropriate impulse response. Enemy aircraft are detected with radar by analyzing a measured impulse response. Echo suppression in long distance telephone calls is accomplished by creating an impulse response that counteracts the impulse response of the reverberation. The list goes on and on. This chapter expands on the properties and usage of convolution in several areas. First, several common impulse responses are discussed. Second, methods are presented for dealing with cascade and parallel combinations of linear systems. Third, the technique of correlation is introduced. Fourth, a nasty problem with convolution is examined, the computation time can be unacceptably long using conventional algorithms and computers. Common Impulse Responses Delta Function The simplest impulse response is nothing more that a delta function, as shown in Fig. 7-1a. That is, an impulse on the input produces an identical impulse on the output. This means that all signals are passed through the system without change. Convolving any signal with a delta function results in exactly the same signal. Mathematically, this is written: EQUATION 7-1 The delta function is the identity for ( ' convolution. Any signal convolved with x[n] *[n] x[n] a delta function is left unchanged. This property makes the delta function the identity for convolution. This is analogous to zero being the identity for addition (a%0 ' a), and one being the identity for multiplication (a×1 ' a).
    [Show full text]
  • 2913 Public Disclosure Authorized
    WPS A 13 POLICY RESEARCH WORKING PAPER 2913 Public Disclosure Authorized Financial Development and Dynamic Investment Behavior Public Disclosure Authorized Evidence from Panel Vector Autoregression Inessa Love Lea Zicchino Public Disclosure Authorized The World Bank Public Disclosure Authorized Development Research Group Finance October 2002 POLIcy RESEARCH WORKING PAPER 2913 Abstract Love and Zicchino apply vector autoregression to firm- availability of internal finance) that influence the level of level panel data from 36 countries to study the dynamic investment. The authors find that the impact of the relationship between firms' financial conditions and financial factors on investment, which they interpret as investment. They argue that by using orthogonalized evidence of financing constraints, is significantly larger in impulse-response functions they are able to separate the countries with less developed financial systems. The "fundamental factors" (such as marginal profitability of finding emphasizes the role of financial development in investment) from the "financial factors" (such as improving capital allocation and growth. This paper-a product of Finance, Development Research Group-is part of a larger effort in the group to study access to finance. Copies of the paper are available free from the World Bank, 1818 H Street NW, Washington, DC 20433. Please contact Kari Labrie, room MC3-456, telephone 202-473-1001, fax 202-522-1155, email address [email protected]. Policy Research Working Papers are also posted on the Web at http://econ.worldbank.org. The authors may be contacted at [email protected] or [email protected]. October 2002. (32 pages) The Policy Research Working Paper Series disseminates the findmygs of work mn progress to encouirage the excbange of ideas about development issues.
    [Show full text]
  • Linear Time Invariant Systems
    UNIT III LINEAR TIME INVARIANT CONTINUOUS TIME SYSTEMS CT systems – Linear Time invariant Systems – Basic properties of continuous time systems – Linearity, Causality, Time invariance, Stability – Frequency response of LTI systems – Analysis and characterization of LTI systems using Laplace transform – Computation of impulse response and transfer function using Laplace transform – Differential equation – Impulse response – Convolution integral and Frequency response. System A system may be defined as a set of elements or functional blocks which are connected together and produces an output in response to an input signal. The response or output of the system depends upon transfer function of the system. Mathematically, the functional relationship between input and output may be written as y(t)=f[x(t)] Types of system Like signals, systems may also be of two types as under: 1. Continuous-time system 2. Discrete time system Continuous time System Continuous time system may be defined as those systems in which the associated signals are also continuous. This means that input and output of continuous – time system are both continuous time signals. For example: Audio, video amplifiers, power supplies etc., are continuous time systems. Discrete time systems Discrete time system may be defined as a system in which the associated signals are also discrete time signals. This means that in a discrete time system, the input and output are both discrete time signals. For example, microprocessors, semiconductor memories, shift registers etc., are discrete time signals. LTI system:- Systems are broadly classified as continuous time systems and discrete time systems. Continuous time systems deal with continuous time signals and discrete time systems deal with discrete time system.
    [Show full text]
  • Schwartz Functions on Nash Manifolds and Applications to Representation Theory
    SCHWARTZ FUNCTIONS ON NASH MANIFOLDS AND APPLICATIONS TO REPRESENTATION THEORY AVRAHAM AIZENBUD Joint with Dmitry Gourevitch and Eitan Sayag arXiv:0704.2891 [math.AG], arxiv:0709.1273 [math.RT] Let us start with the following motivating example. Consider the circle S1, let N ⊂ S1 be the north pole and denote U := S1 n N. Note that U is diffeomorphic to R via the stereographic projection. Consider the space D(S1) of distributions on S1, that is the space of continuous linear functionals on the 1 1 1 Fr´echet space C (S ). Consider the subspace DS1 (N) ⊂ D(S ) consisting of all distributions supported 1 at N. Then the quotient D(S )=DS1 (N) will not be the space of distributions on U. However, it will be the space S∗(U) of Schwartz distributions on U, that is continuous functionals on the Fr´echet space S(U) of Schwartz functions on U. In this case, S(U) can be identified with S(R) via the stereographic projection. The space of Schwartz functions on R is defined to be the space of all infinitely differentiable functions that rapidly decay at infinity together with all their derivatives, i.e. xnf (k) is bounded for any n; k. In this talk we extend the notions of Schwartz functions and Schwartz distributions to a larger geometric realm. As we can see, the definition is of algebraic nature. Hence it would not be reasonable to try to extend it to arbitrary smooth manifolds. However, it is reasonable to extend this notion to smooth algebraic varieties.
    [Show full text]
  • Fundamental Theorems in Mathematics
    SOME FUNDAMENTAL THEOREMS IN MATHEMATICS OLIVER KNILL Abstract. An expository hitchhikers guide to some theorems in mathematics. Criteria for the current list of 243 theorems are whether the result can be formulated elegantly, whether it is beautiful or useful and whether it could serve as a guide [6] without leading to panic. The order is not a ranking but ordered along a time-line when things were writ- ten down. Since [556] stated “a mathematical theorem only becomes beautiful if presented as a crown jewel within a context" we try sometimes to give some context. Of course, any such list of theorems is a matter of personal preferences, taste and limitations. The num- ber of theorems is arbitrary, the initial obvious goal was 42 but that number got eventually surpassed as it is hard to stop, once started. As a compensation, there are 42 “tweetable" theorems with included proofs. More comments on the choice of the theorems is included in an epilogue. For literature on general mathematics, see [193, 189, 29, 235, 254, 619, 412, 138], for history [217, 625, 376, 73, 46, 208, 379, 365, 690, 113, 618, 79, 259, 341], for popular, beautiful or elegant things [12, 529, 201, 182, 17, 672, 673, 44, 204, 190, 245, 446, 616, 303, 201, 2, 127, 146, 128, 502, 261, 172]. For comprehensive overviews in large parts of math- ematics, [74, 165, 166, 51, 593] or predictions on developments [47]. For reflections about mathematics in general [145, 455, 45, 306, 439, 99, 561]. Encyclopedic source examples are [188, 705, 670, 102, 192, 152, 221, 191, 111, 635].
    [Show full text]
  • Mathematical Problems on Generalized Functions and the Can–
    Mathematical problems on generalized functions and the canonical Hamiltonian formalism J.F.Colombeau [email protected] Abstract. This text is addressed to mathematicians who are interested in generalized functions and unbounded operators on a Hilbert space. We expose in detail (in a “formal way”- as done by Heisenberg and Pauli - i.e. without mathematical definitions and then, of course, without mathematical rigour) the Heisenberg-Pauli calculations on the simplest model close to physics. The problem for mathematicians is to give a mathematical sense to these calculations, which is possible without any knowledge in physics, since they mimick exactly usual calculations on C ∞ functions and on bounded operators, and can be considered at a purely mathematical level, ignoring physics in a first step. The mathematical tools to be used are nonlinear generalized functions, unbounded operators on a Hilbert space and computer calculations. This text is the improved written version of a talk at the congress on linear and nonlinear generalized functions “Gf 07” held in Bedlewo-Poznan, Poland, 2-8 September 2007. 1-Introduction . The Heisenberg-Pauli calculations (1929) [We,p20] are a set of 3 or 4 pages calculations (in a simple yet fully representative model) that are formally quite easy and mimick calculations on C ∞ functions. They are explained in detail at the beginning of this text and in the appendices. The H-P calculations [We, p20,21, p293-336] are a basic formulation in Quantum Field Theory: “canonical Hamiltonian formalism”, see [We, p292] for their relevance. The canonical Hamiltonian formalism is considered as mainly equivalent to the more recent “(Feynman) path integral formalism”: see [We, p376,377] for the connections between the 2 formalisms that complement each other.
    [Show full text]