Parallel Scans & Prefix Sums
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Parallel Prefix Sum (Scan) with CUDA
Parallel Prefix Sum (Scan) with CUDA Mark Harris [email protected] April 2007 Document Change History Version Date Responsible Reason for Change February 14, Mark Harris Initial release 2007 April 2007 ii Abstract Parallel prefix sum, also known as parallel Scan, is a useful building block for many parallel algorithms including sorting and building data structures. In this document we introduce Scan and describe step-by-step how it can be implemented efficiently in NVIDIA CUDA. We start with a basic naïve algorithm and proceed through more advanced techniques to obtain best performance. We then explain how to scan arrays of arbitrary size that cannot be processed with a single block of threads. Month 2007 1 Parallel Prefix Sum (Scan) with CUDA Table of Contents Abstract.............................................................................................................. 1 Table of Contents............................................................................................... 2 Introduction....................................................................................................... 3 Inclusive and Exclusive Scan .........................................................................................................................3 Sequential Scan.................................................................................................................................................4 A Naïve Parallel Scan ......................................................................................... 4 A Work-Efficient -

Generic Implementation of Parallel Prefix Sums and Their
GENERIC IMPLEMENTATION OF PARALLEL PREFIX SUMS AND THEIR APPLICATIONS A Thesis by TAO HUANG Submitted to the Office of Graduate Studies of Texas A&M University in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE May 2007 Major Subject: Computer Science GENERIC IMPLEMENTATION OF PARALLEL PREFIX SUMS AND THEIR APPLICATIONS A Thesis by TAO HUANG Submitted to the Office of Graduate Studies of Texas A&M University in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE Approved by: Chair of Committee, Lawrence Rauchwerger Committee Members, Nancy M. Amato Jennifer L. Welch Marvin L. Adams Head of Department, Valerie E. Taylor May 2007 Major Subject: Computer Science iii ABSTRACT Generic Implementation of Parallel Prefix Sums and Their Applications. (May 2007) Tao Huang, B.E.; M.E., University of Electronic Science and Technology of China Chair of Advisory Committee: Dr. Lawrence Rauchwerger Parallel prefix sums algorithms are one of the simplest and most useful building blocks for constructing parallel algorithms. A generic implementation is valuable because of the wide range of applications for this method. This thesis presents a generic C++ implementation of parallel prefix sums. The implementation applies two separate parallel prefix sums algorithms: a recursive doubling (RD) algorithm and a binary-tree based (BT) algorithm. This implementation shows how common communication patterns can be sepa- rated from the concrete parallel prefix sums algorithms and thus simplify the work of parallel programming. For each algorithm, the implementation uses two different synchronization options: barrier synchronization and point-to-point synchronization. These synchronization options lead to different communication patterns in the algo- rithms, which are represented by dependency graphs between tasks. -
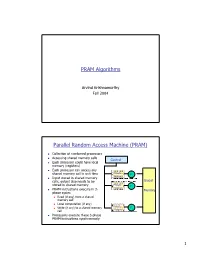
PRAM Algorithms Parallel Random Access Machine
PRAM Algorithms Arvind Krishnamurthy Fall 2004 Parallel Random Access Machine (PRAM) n Collection of numbered processors n Accessing shared memory cells Control n Each processor could have local memory (registers) n Each processor can access any shared memory cell in unit time Private P Memory 1 n Input stored in shared memory cells, output also needs to be Global stored in shared memory Private P Memory 2 n PRAM instructions execute in 3- Memory phase cycles n Read (if any) from a shared memory cell n Local computation (if any) Private n Write (if any) to a shared memory P Memory p cell n Processors execute these 3-phase PRAM instructions synchronously 1 Shared Memory Access Conflicts n Different variations: n Exclusive Read Exclusive Write (EREW) PRAM: no two processors are allowed to read or write the same shared memory cell simultaneously n Concurrent Read Exclusive Write (CREW): simultaneous read allowed, but only one processor can write n Concurrent Read Concurrent Write (CRCW) n Concurrent writes: n Priority CRCW: processors assigned fixed distinct priorities, highest priority wins n Arbitrary CRCW: one randomly chosen write wins n Common CRCW: all processors are allowed to complete write if and only if all the values to be written are equal A Basic PRAM Algorithm n Let there be “n” processors and “2n” inputs n PRAM model: EREW n Construct a tournament where values are compared P0 Processor k is active in step j v if (k % 2j) == 0 At each step: P0 P4 Compare two inputs, Take max of inputs, P0 P2 P4 P6 Write result into shared memory -

Parallel Prefix Sum on the GPU (Scan)
Parallel Prefix Sum on the GPU (Scan) Presented by Adam O’Donovan Slides adapted from the online course slides for ME964 at Wisconsin taught by Prof. Dan Negrut and from slides Presented by David Luebke Parallel Prefix Sum (Scan) Definition: The all-prefix-sums operation takes a binary associative operator ⊕ with identity I, and an array of n elements a a a [ 0, 1, …, n-1] and returns the ordered set I a a ⊕ a a ⊕ a ⊕ ⊕ a [ , 0, ( 0 1), …, ( 0 1 … n-2)] . Example: Exclusive scan: last input if ⊕ is addition, then scan on the set element is not included in [3 1 7 0 4 1 6 3] the result returns the set [0 3 4 11 11 15 16 22] (From Blelloch, 1990, “Prefix 2 Sums and Their Applications) Applications of Scan Scan is a simple and useful parallel building block Convert recurrences from sequential … for(j=1;j<n;j++) out[j] = out[j-1] + f(j); … into parallel : forall(j) in parallel temp[j] = f(j); scan(out, temp); Useful in implementation of several parallel algorithms: radix sort Polynomial evaluation quicksort Solving recurrences String comparison Tree operations Lexical analysis Histograms Stream compaction Etc. HK-UIUC 3 Scan on the CPU void scan( float* scanned, float* input, int length) { scanned[0] = 0; for(int i = 1; i < length; ++i) { scanned[i] = scanned[i-1] + input[i-1]; } } Just add each element to the sum of the elements before it Trivial, but sequential Exactly n-1 adds: optimal in terms of work efficiency 4 Parallel Scan Algorithm: Solution One Hillis & Steele (1986) Note that a implementation of the algorithm shown in picture requires two buffers of length n (shown is the case n=8=2 3) Assumption: the number n of elements is a power of 2: n=2 M Picture courtesy of Mark Harris 5 The Plain English Perspective First iteration, I go with stride 1=2 0 Start at x[2 M] and apply this stride to all the array elements before x[2 M] to find the mate of each of them. -

Combinatorial Species and Labelled Structures Brent Yorgey University of Pennsylvania, [email protected]
University of Pennsylvania ScholarlyCommons Publicly Accessible Penn Dissertations 1-1-2014 Combinatorial Species and Labelled Structures Brent Yorgey University of Pennsylvania, [email protected] Follow this and additional works at: http://repository.upenn.edu/edissertations Part of the Computer Sciences Commons, and the Mathematics Commons Recommended Citation Yorgey, Brent, "Combinatorial Species and Labelled Structures" (2014). Publicly Accessible Penn Dissertations. 1512. http://repository.upenn.edu/edissertations/1512 This paper is posted at ScholarlyCommons. http://repository.upenn.edu/edissertations/1512 For more information, please contact [email protected]. Combinatorial Species and Labelled Structures Abstract The theory of combinatorial species was developed in the 1980s as part of the mathematical subfield of enumerative combinatorics, unifying and putting on a firmer theoretical basis a collection of techniques centered around generating functions. The theory of algebraic data types was developed, around the same time, in functional programming languages such as Hope and Miranda, and is still used today in languages such as Haskell, the ML family, and Scala. Despite their disparate origins, the two theories have striking similarities. In particular, both constitute algebraic frameworks in which to construct structures of interest. Though the similarity has not gone unnoticed, a link between combinatorial species and algebraic data types has never been systematically explored. This dissertation lays the theoretical groundwork for a precise—and, hopefully, useful—bridge bewteen the two theories. One of the key contributions is to port the theory of species from a classical, untyped set theory to a constructive type theory. This porting process is nontrivial, and involves fundamental issues related to equality and finiteness; the recently developed homotopy type theory is put to good use formalizing these issues in a satisfactory way. -

Algorithms Based on Parallel Prefix (Scan) Operations, Cont
COMP 322: Fundamentals of Parallel Programming Lecture 38: Algorithms based on Parallel Prefix (Scan) operations, cont. Mack Joyner and Zoran Budimlić {mjoyner, zoran}@rice.edu Acknowledgements: • Book chapter on “Prefix Sums and Their Applications”, Guy E. Blelloch, CMU • Slides on “Parallel prefix adders”, Kostas Vitoroulis, Concordia University http://comp322.rice.edu COMP 322 Lecture 38 April 2018 Worksheet #37 problem statement: Parallelizing the Split step in Radix Sort The Radix Sort algorithm loops over the bits in the binary representation of the keys, starting at the lowest bit, and executes a split operation for each bit as shown below. The split operation packs the keys with a 0 in the corresponding bit to the bottom of a vector, and packs the keys with a 1 to the top of the same vector. It maintains the order within both groups. The sort works because each split operation sorts the keys with respect to the current bit and maintains the sorted order of all the lower bits. Your task is to show how the split operation can be performed in parallel using scan operations, and to explain your answer. [101 111 011 001 100 010 111 010] 1.A = [5 7 3 1 4 2 7 2] 2.A⟨0⟩ = [1 1 1 1 0 0 1 0] //lowest bit 3.A←split(A,A⟨0⟩) = [4 2 2 5 7 3 1 7] 4.A⟨1⟩ = [0 1 1 0 1 1 0 1] // middle bit 5.A←split(A,A⟨1⟩) = [4 5 1 2 2 7 3 7] 6.A⟨2⟩ = [1 1 0 0 0 1 0 1] // highest bit 7.A←split(A,A⟨2⟩) = [1 2 2 3 4 5 7 7] 2 COMP 322, Spring 2018 (M.Joyner, Z. -

MPI Collectives I: Reductions and Broadcast Calculating Pi with a Broadcast and Reduction
MPI Collectives I: Reductions and broadcast Calculating Pi with a broadcast and reduction UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN © 2018 L. V. Kale at the University of Illinois Urbana What does “Collective” mean • Everyone within the communicator (named in the call) must make that call before the call can be effected • Essentially, a collective call requires coordination among all the processes of a communicator L.V.Kale 2 Some Basic MPI Collective Calls • MPI_Barrier(MPI_Comm comm) • Blocks the caller until all processes have entered the call • MPI_Bcast(void* buffer, int count, MPI_Datatype datatype, int root, MPI_Comm comm) • Broadcasts a message from rank ‘root’ to all processes of the group • It is called by all members of group using the same arguments • MPI_Allreduce(void* sendbuf, void* recvbuf, int count, MPI_Datatype datatype, MPI_Op op, MPI_Comm comm) • MPI_Reduce(void* sendbuf, void* recvbuf, int count, MPI_Datatype datatype, MPI_Op op, int root, MPI_Comm comm) L.V.Kale 3 PI Example with Broadcast and reductions int main(int argc, char **argv) { int myRank, numPes; MPI_Init(&argc, &argv); MPI_Comm_size(MPI_COMM_WORLD, &numPes); MPI_Comm_rank(MPI_COMM_WORLD, &myRank); int count, i, numTrials, myTrials; if(myRank == 0) { scanf("%d", &numTrials); myTrials = numTrials / numPes; numTrials = myTrials * numPes; // takes care of rounding } MPI_BcastMPI_Bcast(&(&myTrialsmyTrials,, 1,1, MPI_INT,MPI_INT, 0,0, MPI_COMM_WORLD);MPI_COMM_WORLD); count = 0; srandom(myRank); double x, y, pi; L.V.Kale 4 // code continues from the last page... for (i=0; i<myTrials; i++) { x = (double) random()/RAND_MAX; y = (double) random()/RAND_MAX; if (x*x + y*y < 1.0) count++; } int globalCount = 0; MPI_Allreduce(&count, &globalCount, 1, MPI_INT, MPI_SUM, MPI_COMM_WORLD); pi = (double)(4 * globalCount) / (myTrials * numPes); printf("[%d] pi = %f\n", myRank, pi); MPI_Finalize(); return 0; } /* end function main */ L.V.Kale 5 MPI_Reduce • Often, you want the result of a reduction only on one processors • E.g. -

Appendix Mathematical Background A
Appendix Mathematical Background A Sum Formulas Each sum of the form n xk = 1k + 2k + 3k +···+nk, x=1 where k is a positive integer has a closed-form formula that is a polynomial of degree k + 1. For example,1 n n(n + 1) x = 1 + 2 + 3 +···+n = 2 x=1 and n n(n + 1)(2n + 1) x2 = 12 + 22 + 32 + ...+ n2 = . 6 x=1 An arithmetic progression is a sequence of numbers where the difference between any two consecutive numbers is constant. For example, 3, 7, 11, 15 is an arithmetic progression with constant 4. The sum of an arithmetic progression can be calculated using the formula n(a + b) a +···+b = 2 n numbers 1There is even a general formula for such sums, called Faulhaber’s formula, but it is too complex to be presented here. © Springer International Publishing AG, part of Springer Nature 2017 269 A. Laaksonen, Guide to Competitive Programming, Undergraduate Topics in Computer Science, https://doi.org/10.1007/978-3-319-72547-5 270 Appendix A: Mathematical Background where a is the first number, b is the last number, and n is the amount of numbers. For example, 4 · (3 + 15) 3 + 7 + 11 + 15 = = 36. 2 The formula is based on the fact that the sum consists of n numbers and the value of each number is (a + b)/2 on average. A geometric progression is a sequence of numbers where the ratio between any two consecutive numbers is constant. For example, 3, 6, 12, 24 is a geometric progression with constant 2. -

A Sound and Complete Abstraction for Reasoning About Parallel Prefix
In proceedings of POPL’14 A Sound and Complete Abstraction for Reasoning about Parallel Prefix Sums ∗ Nathan Chong Alastair F. Donaldson Jeroen Ketema Imperial College London fnyc04,afd,[email protected] Abstract 1. Introduction Prefix sums are key building blocks in the implementation of many The prefix sum operation, which given an array A computes an concurrent software applications, and recently much work has gone array B consisting of all sums of prefixes of A, is an important into efficiently implementing prefix sums to run on massively par- building block in many high performance computing applications. allel graphics processing units (GPUs). Because they lie at the heart A key example is stream compaction: suppose a group of n threads of many GPU-accelerated applications, the correctness of prefix has calculated a number of data items in parallel, each thread t sum implementations is of prime importance. (1 ≤ t ≤ n) having computed dt items; now the threads must We introduce a novel abstraction, the interval of summations, write the resulting items to a shared array out in a compact manner, that allows scalable reasoning about implementations of prefix i.e. thread t should write its items to a series of dt indices of sums. We present this abstraction as a monoid, and prove a sound- out starting from position d1 + ··· + dt−1. Compacting the data ness and completeness result showing that a generic sequential pre- stream by serialising the threads, so that thread 1 writes its results, fix sum implementation is correct for an array of length n if and followed by thread 2, etc., would be slow. -

Designing Efficient Parallel Prefix Sum Algorithms for Gpus
Designing Efficient Parallel Prefix Sum Algorithms for GPUs Gabriele Capannini Information Science and Technology Institute of the National Research Council Pisa, Italy Email: [email protected] Abstract—This paper presents a novel and efficient method Ding et al. [4] use prefix sum to implement their PForDelta to compute one of the simplest and most useful building block decoder for accessing postings lists, and a number of other for parallel algorithms: the parallel prefix sum operation. applications refer to this operation [5], [6]. Besides its practical relevance, the problem achieves further interest in parallel-computation theory. Concerning the computational complexity on a sequential We firstly describe step-by-step how parallel prefix sum processor, prefix sum operation is linear in the size of the is performed in parallel on GPUs. Next we propose a more input list. Instead when the computation is performed in par- efficient technique properly developed for modern graphics allel the complexity becomes logarithmic [7], [8], [9]. On the processors and alike processors. Our technique is able to one hand, the sequential solution is more easy to implement perform the computation in such a way that minimizes both memory conflicts and memory usage. and works in-place. As a consequence, if the available degree Finally we evaluate theoretically and empirically all the of parallelism is low, the approaches based on the sequential considered solutions in terms of efficiency, space complexity, solution could be still applied without major performance and computational time. In order to properly conduct the loss. On the other hand, it is straightforward that, augment- theoretical analysis we used a novel computational model ing the parallelism degree, the efficient prefix sum computa- proposed by us in a previous work: K-model. -

Parallel Prefix Adders
Parallel prefix adders Kostas Vitoroulis, 2006. Presented to Dr. A. J. Al-Khalili. Concordia University. Overview of presentation Parallel prefix operations Binary addition as a parallel prefix operation Prefix graphs Adder topologies Summary Parallel Prefix Operation Terminology background: Prefix: The outcome of the operation depends on the initial inputs. Parallel: Involves the execution of an operation in parallel. This is done by segmentation into smaller pieces that are computed in parallel. Operation: Any arbitrary primitive operator “ ° ” that is associative is parallelizable it is fast because the processing is accomplished in a parallel fashion. Example: Associative operations are parallelizable Consider the logical OR operation: a + b The operation is associative: a + b + c + d = ((( a + b ) + c) + d ) = (( a + b ) + ( c + d)) Serial implementation: Parallel implementation: Mathematical Formulation: Prefix Sum “°” Å this is the unary operator Operator: known as “scan” or “prefix sum” Input is a vector: A = AnAn-1 …A1 Output is another vector: B = BnBn-1 …B1 where B1 = A1 B2 = A1 ° A2 Å Bn represents the … operator being applied to Bn= A1 ° A2 … ° An all terms of the vector. Example of prefix sum Consider the vector: A = AnAn-1 …A1 where element Ai is an integer The “*” unary operator, defined as: *A = B With B = BnBn-1 …B1 B1 = A1 B2 = A1 * A2 B3 = A1 * A1 * A3 … and ‘ * ’ here is the integer addition operation. Example of prefix sum Calculation of *A, where A = 6 5 4 3 2 1 yields: B = *A = 21 15 10 6 3 1 Because the summation is associative the calculation can be done in parallel in the following manner: Parallel implementation versus Serial implementation 6 5 4 3 2 1 6 5 4 3 2 1 + + + + + + + BB6 =3 BA=621 +…(A= A1A+A11+1 += A A12)2 =+ 3 A3 = (A6 + A+5) + + + = 6 ((A+4+A3) +(A2 +A1)) += 21 B6 B5 B4 B3 B2 B1 B6 B5 B4 B3 B2 B1 This is the pen and paper addition of Binary Addition two 4-bit binary numbers x and y. -

Competitive Programmer's Handbook
Competitive Programmer’s Handbook Antti Laaksonen Draft August 19, 2019 ii Contents Preface ix I Basic techniques 1 1 Introduction 3 1.1 Programming languages . .3 1.2 Input and output . .4 1.3 Working with numbers . .6 1.4 Shortening code . .8 1.5 Mathematics . 10 1.6 Contests and resources . 15 2 Time complexity 17 2.1 Calculation rules . 17 2.2 Complexity classes . 20 2.3 Estimating efficiency . 21 2.4 Maximum subarray sum . 21 3 Sorting 25 3.1 Sorting theory . 25 3.2 Sorting in C++ . 29 3.3 Binary search . 31 4 Data structures 35 4.1 Dynamic arrays . 35 4.2 Set structures . 37 4.3 Map structures . 38 4.4 Iterators and ranges . 39 4.5 Other structures . 41 4.6 Comparison to sorting . 44 5 Complete search 47 5.1 Generating subsets . 47 5.2 Generating permutations . 49 5.3 Backtracking . 50 5.4 Pruning the search . 51 5.5 Meet in the middle . 54 iii 6 Greedy algorithms 57 6.1 Coin problem . 57 6.2 Scheduling . 58 6.3 Tasks and deadlines . 60 6.4 Minimizing sums . 61 6.5 Data compression . 62 7 Dynamic programming 65 7.1 Coin problem . 65 7.2 Longest increasing subsequence . 70 7.3 Paths in a grid . 71 7.4 Knapsack problems . 72 7.5 Edit distance . 74 7.6 Counting tilings . 75 8 Amortized analysis 77 8.1 Two pointers method . 77 8.2 Nearest smaller elements . 79 8.3 Sliding window minimum . 81 9 Range queries 83 9.1 Static array queries .