DOCSLIB.ORG

Limits on the Masses of Supersymmetric Particles from the UA1 Experiment at the CERN Protek=As±Ipr©Ten

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Limits on the Masses of Supersymmetric Particles from the UA1 Experiment at the CERN Protek=As±Ipr©Ten Limits on the masses of supersymmetric particles from the UA1 experiment at the CERN proteK=as±ipr©ten. collider ?? Afzal Khan Imperial College L on don A thesis submitted to the University of London for the degree of Doctor of Philosophy ABSTRACT An analysis is presented of a data sample with large missing transverse energy, recorded at the CERN proton-antiproton collider. The data were collected at the UA1 experiment and correspond to, an integrated luminosity of 715 nb"1. A description of the Monte-Carlo calculations is given, for processes contributing to this large E>j.miss data sample. The very good agreement between the data and the simulated Standard Model physics processes is then used to set mass limits on the existence of the supersymmetric partners of the intermediate vector bosons, quarks and gluons - with the assumption of a massless lightest supersymmetric particle(taken to be a photino). Variation of the mass limits with a massive photino is also investigated. ACKNOWLEDGEMENTS Before I embark upon the impossible task of recognising all those who have contributed to the fabric of my existence as a postgraduate student, I must apologise to them, who, partly through the exigencies of space and mostly through the deficiency of my recollection, have remained unmentioned. I doubt, however, if such neglect should cause them too much uneasiness of mind. I should like to give thanks to the Science and Engineering Research Council for the financial support with which I have been provided. Many thanks are due to Dave Binnie for allowing me to join the HEP group and for providing the opportunity to spend a most fruitful time at CERN. To Jim Virdee, whose tenacious assiduity was surpassed only by his effusive criticism, I doff the proverbial hat. Without him the inclination of the path may have been more sorely felt. I should also like to express my unbounded gratitude to Chris Seez, who through a combination of eccentric humour and unquestionable competence, created an atmosphere not lacking of spice. His help with that of Tony Wildish, in the early days, was vital. My thanks go to Dave Robinson for his tranquillity^to Christos Markou for his companionship, to Roger Forty for revealing to me the possibility of a future in squash, to Lucas Taylor for his help with some histograms, to Steve Macmahon for providing me with the opportunity to lose his key and to Shaun Roe for sharing in the masochism of excessive physical exercise. I thank also Alan Watson, Marco Cattaneo, Gary Taylor, Julian Shulman, Sylvie Dugaey, James Gillies, Rob Edgecock, Nav Bains and Dave Francis for their camaraderie. I am grateful to Steve Haywood for sharing with me the last bus and to Dave Charlton for rendering it unnecessary to take an axe to the machine. I am indebted to Mohammad Mohammadi, Felicitas Pauss and Richard Batley, whose help with the missing energy analysis was invaluable. Page 2 Special thanks are due to Linda Jones, in whose foot I have been a constant thorn. Perhaps it was the use of this afflicted appendage that caused her to miss the penalty, which was as unlikely an event as the rising of the sun in the middle of the night, and thereby ensure that we achieved national notoriety by losing everything yet again. Thanks also to Betty Moynihan for fussing over the inexorable increase of entropy in my office, To Jim Gibb for ensuring that the greater part of humanity is acquainted with the ’rubber king' anecdote, to Diane, to Ash and also to Jane Ratcliffe for enduring when most had fallen by the wayside(part-timers). I thank, also, John Hassard for checking the spelling. To Jeremy Dodd I express my gratitude for being such a work of art and for showing me that something does turn up. I thank Miles Blencowe for making the effort to descend, occasionally, into our four dimensions. I thank Leslie Marshall for being an affectionate friend to me and quite probably to the rest of the world, Mike Huricane for giving me an appreciation of speed and Maria for possessing a caustic wit. Davie Norman, that one-man show, is surely above appreciation. Watching him pursue a ball to the boundary is truly a sight to behold (beheld all to often, I may add, when playing for CERN). My thanks to Julian and Sian for providing the most delightful society and to Steve Hancock, to whom my advice must surely be to stay on the front foot. Finally, I have the greatest pleasure to express my eternal gratitude to Alison Fowler, the gang and to my mother, Gulzar Begum. Without their love, support and unqualified commitment, the flowers would not blossom, the birds would not sing, the sun would not shine and, discord would reign supreme. London September 1989. Page 3 To my mother and the loving memory of my dear father. CONTENTS ABSTRACT 1 ACKNOWLEDGEMENTS 2 CONTENTS 5 1. THEORETICAL INTRODUCTION 8 1.1 Introduction 8 12 Standard Model 9 13 Supersymmetry 12 2. EXPERIMENTAL INTRODUCTION 19 21 The CERN proton-antiproton project 19 22 Beam cooling 21 23 Physics on UA1 22 24 Missing transverse energy 23 3. THE UA1 APPARATUS 27 3.1 Introduction 27 3.2 The central detector 28 3.3 The electromagnetic calorimeters 30 Page 5 3.4 The hadron calorimeters 32 35 The muon chambers 33 3.6 The forward chambers 33 3.7 The trigger 34 3.8 Data acquisition and reconstruction 35 4. JET FINDING AND THE MISSING ENERGY TECHNIQUE 45 4.1 Introduction 45 4.2 The UA1 jet algorithm 46 4.3 The jet energy 47 4.4 The missing transverse energy technique 48 4.5 Other sources of missing transverse energy 50 4.6 The jet-fluctuation Monte Carlo 51 5. THE MISSING TRANSVERSE ENERGY DATA SAMPLE AND THE STANDARD MODEL CONTRIBUTIONS 57 5.1 Introduction 57 5.2 The Hardware triggers 58 5.3 The on-line selection 59 5.4 The off-line selection 59 55 Standard Model contributions 62 55.1 Monte Carlo results 63 5.5.2 Separation of the W—>rv signal 64 5.55 Systematic errors 66 55.4 Non-tau sample 66 6. MASS LIMITS ON THE SUPERSYMMETRIC PARTICLES ' 83 6.1 Introduction 83 6.2 The supersymmetric model 84 6.2.1 Production of the gauginos 85 6.2.2 Decay of the gauginos 88 Page 6 6.3 Simulation of the supersymmetric processes 89 6.4 Results for the massless photino scenario 90 6.4.1 Properites of the massless photino events 91 6.4.2 The wino mass limit for the massless photino scenario 92 6.5 Results for the massive photino scenario 93 65.1 Properties of the massive photino events 94 65.2 The wino mass limit for the massive photino scenario 94 6.6 Limits on the masses of the supersymmetric partners of the quarks and gluons 95 6.6.1 The data sample 96 6.6.2 The Standard Model background 96 6.6.3 The supersymmetric model 97 6.6.4 Results 98 7. CONCLUSIONS 122 Appendix A : The specific form of the gaugino lagrangian and the couplings 124 A ppendix B : The statistical method used to derive the mass limits 129 REFERENCES 132 Page 7 CHAPTER 1 THEORETICAL INTRODUCTION 1.1 INTRODUCTION The current theoretical description of the physical world, which is often referred to as the Standard Model [14], has been very successful in its description of nearly all available data pertaining to the strong, weak and electromagnetic phenomena, and as yet there is no evidence of behaviour that violates this scheme. The Standard Model does not, however, represent a complete unified theory of all the interactions in nature. There are theoretical and aesthetic arguments which suggest that an extension of the Standard Model will be needed. Supersymmetry is a recent theoretical idea which represents a potentially significant addition to our current understanding of the physical world. It offers many promising avenues in the attempt to construct a unified field theory of physics and alleviates some of the shortcomings of the Standard Model. This chapter contains a brief history of particle physics and a qualitative description of the Standard Model. It ends with a discussion of the theoretical motivation for and the phenomenology of, supersymmetry. Page 8 1.2 STANDARD MODEL The eighteenth century saw the maturation of classical mechanics, and the advent of the theory of classical electromagnetism. This was followed early in the twentieth century by two major new conceptual frameworks, quantum mechanics and relativity theory. These were brought together in 1928 by Dirac [15] and together with Maxwell's theory of electromagnetism, represent a body of knowledge sufficient to understand the interactions of atoms and molecules, which form the basis for all chemistry and ultimately biology. During the 1940’s theorists such as Schwinger, Feynman and Tomonaga [16] created a complete quantum field theory of electrodynamics, QED. The central mathematical idea was that of a lagrangian, which together with Hamilton's least action principle yields the field equations of motion (from the Euler-Lagrange equations). By the 1940’s the existence of the four forces of nature, gravitation, electromagnetism, weak and strong, was known. These four forces are still considered fundamental today, although a connection between the weak and the electromagnetic forces has now been recognised. The 1940’s also saw the set of known particles increase from the simple set of five known in the 1930’s , i.e. protons, neutrons, electrons, photons and neutrinos. The proton, neutron and electron are known to be constituents of atoms, while the photon is known to transmit the electromagnetic force.
Load more

Recommended publications
  • Quantum Field Theory*
    Quantum Field Theory y Frank Wilczek Institute for Advanced Study, School of Natural Science, Olden Lane, Princeton, NJ 08540 I discuss the general principles underlying quantum eld theory, and attempt to identify its most profound consequences. The deep est of these consequences result from the in nite number of degrees of freedom invoked to implement lo cality.Imention a few of its most striking successes, b oth achieved and prosp ective. Possible limitation s of quantum eld theory are viewed in the light of its history. I. SURVEY Quantum eld theory is the framework in which the regnant theories of the electroweak and strong interactions, which together form the Standard Mo del, are formulated. Quantum electro dynamics (QED), b esides providing a com- plete foundation for atomic physics and chemistry, has supp orted calculations of physical quantities with unparalleled precision. The exp erimentally measured value of the magnetic dip ole moment of the muon, 11 (g 2) = 233 184 600 (1680) 10 ; (1) exp: for example, should b e compared with the theoretical prediction 11 (g 2) = 233 183 478 (308) 10 : (2) theor: In quantum chromo dynamics (QCD) we cannot, for the forseeable future, aspire to to comparable accuracy.Yet QCD provides di erent, and at least equally impressive, evidence for the validity of the basic principles of quantum eld theory. Indeed, b ecause in QCD the interactions are stronger, QCD manifests a wider variety of phenomena characteristic of quantum eld theory. These include esp ecially running of the e ective coupling with distance or energy scale and the phenomenon of con nement.
    [Show full text]
  • Wimps and Machos ENCYCLOPEDIA of ASTRONOMY and ASTROPHYSICS
    WIMPs and MACHOs ENCYCLOPEDIA OF ASTRONOMY AND ASTROPHYSICS WIMPs and MACHOs objects that could be the dark matter and still escape detection. For example, if the Galactic halo were filled –3 . WIMP is an acronym for weakly interacting massive par- with Jupiter mass objects (10 Mo) they would not have ticle and MACHO is an acronym for massive (astrophys- been detected by emission or absorption of light. Brown . ical) compact halo object. WIMPs and MACHOs are two dwarf stars with masses below 0.08Mo or the black hole of the most popular DARK MATTER candidates. They repre- remnants of an early generation of stars would be simi- sent two very different but reasonable possibilities of larly invisible. Thus these objects are examples of what the dominant component of the universe may be. MACHOs. Other examples of this class of dark matter It is well established that somewhere between 90% candidates include primordial black holes created during and 99% of the material in the universe is in some as yet the big bang, neutron stars, white dwarf stars and vari- undiscovered form. This material is the gravitational ous exotic stable configurations of quantum fields, such glue that holds together galaxies and clusters of galaxies as non-topological solitons. and plays an important role in the history and fate of the An important difference between WIMPs and universe. Yet this material has not been directly detected. MACHOs is that WIMPs are non-baryonic and Since extensive searches have been done, this means that MACHOS are typically (but not always) formed from this mysterious material must not emit or absorb appre- baryonic material.
    [Show full text]
  • Zero-Point Energy in Bag Models
    Ooa/ea/oHsnif- ^*7 ( 4*0 0 1 5 4 3 - m . Zero-Point Energy in Bag Models by Kimball A. Milton* Department of Physics The Ohio State University Columbus, Ohio 43210 A b s t r a c t The zero-point (Casimir) energy of free vector (gluon) fields confined to a spherical cavity (bag) is computed. With a suitable renormalization the result for eight gluons is This result is substantially larger than that for a spher­ ical shell (where both interior and exterior modes are pre­ sent), and so affects Johnson's model of the QCD vacuum. It is also smaller than, and of opposite sign to the value used in bag model phenomenology, so it will have important implications there. * On leave ifrom Department of Physics, University of California, Los Angeles, CA 90024. I. Introduction Quantum chromodynamics (QCD) may we 1.1 be the appropriate theory of hadronic matter. However, the theory is not at all well understood. It may turn out that color confinement is roughly approximated by the phenomenologically suc­ cessful bag model [1,2]. In this model, the normal vacuum is a perfect color magnetic conductor, that iis, the color magnetic permeability n is infinite, while the vacuum.in the interior of the bag is characterized by n=l. This implies that the color electric and magnetic fields are confined to the interior of the bag, and that they satisfy the following boundary conditions on its surface S: n.&jg= 0, nxBlg= 0, (1) where n is normal to S. Now, even in an "empty" bag (i.e., one containing no quarks) there will be non-zero fields present because of quantum fluctua­ tions.
    [Show full text]
  • 18. Lattice Quantum Chromodynamics
    18. Lattice QCD 1 18. Lattice Quantum Chromodynamics Updated September 2017 by S. Hashimoto (KEK), J. Laiho (Syracuse University) and S.R. Sharpe (University of Washington). Many physical processes considered in the Review of Particle Properties (RPP) involve hadrons. The properties of hadrons—which are composed of quarks and gluons—are governed primarily by Quantum Chromodynamics (QCD) (with small corrections from Quantum Electrodynamics [QED]). Theoretical calculations of these properties require non-perturbative methods, and Lattice Quantum Chromodynamics (LQCD) is a tool to carry out such calculations. It has been successfully applied to many properties of hadrons. Most important for the RPP are the calculation of electroweak form factors, which are needed to extract Cabbibo-Kobayashi-Maskawa (CKM) matrix elements when combined with the corresponding experimental measurements. LQCD has also been used to determine other fundamental parameters of the standard model, in particular the strong coupling constant and quark masses, as well as to predict hadronic contributions to the anomalous magnetic moment of the muon, gµ 2. − This review describes the theoretical foundations of LQCD and sketches the methods used to calculate the quantities relevant for the RPP. It also describes the various sources of error that must be controlled in a LQCD calculation. Results for hadronic quantities are given in the corresponding dedicated reviews. 18.1. Lattice regularization of QCD Gauge theories form the building blocks of the Standard Model. While the SU(2) and U(1) parts have weak couplings and can be studied accurately with perturbative methods, the SU(3) component—QCD—is only amenable to a perturbative treatment at high energies.
    [Show full text]
  • MASTER THESIS Linking the B-Physics Anomalies and Muon G
    MSc PHYSICS AND ASTRONOMY GRAVITATION, ASTRO-, AND PARTICLE PHYSICS MASTER THESIS Linking the B-physics Anomalies and Muon g − 2 A Phenomenological Study Beyond the Standard Model By Anders Rehult 12623881 February - October 2020 60 EC Supervisor/Examiner: Second Examiner: prof. dr. Robert Fleischer prof. dr. Piet Mulders i Abstract The search for physics beyond the Standard Model is guided by anomalies: discrepancies between the theoretical predictions and experimental measurements of physical quantities. Hints of new physics are found in the recently observed B-physics anomalies and the long-standing anomalous magnetic dipole moment of the muon, muon g − 2. The former include a group of anomalous measurements related to the quark-level transition b ! s. We investigate what features are required of a theory to explain these b ! s anomalies simultaneously with muon g − 2. We then consider three kinds of models that might explain the anomalies: models with leptoquarks, hypothetical particles that couple leptons to quarks; Z0 models, which contain an additional fundamental force and a corresponding force carrier; and supersymmetric scenarios that postulate a symmetry that gives rise to a partner for each SM particle. We identify a leptoquark model that carries the necessary features to explain both kinds of anomalies. Within this model, we study the behaviour of 0 muon g − 2 and the anomalous branching ratio of Bs mesons, bound states of b and s quarks, into muons. 0 ¯0 0 ¯0 The Bs meson can spontaneously oscillate into its antiparticle Bs , a phenomenon known as Bs −Bs mixing. We calculate the effects of this mixing on the anomalous branching ratio.
    [Show full text]
  • Quantum Mechanics Quantum Chromodynamics (QCD)
    Quantum Mechanics_quantum chromodynamics (QCD) In theoretical physics, quantum chromodynamics (QCD) is a theory ofstrong interactions, a fundamental forcedescribing the interactions between quarksand gluons which make up hadrons such as the proton, neutron and pion. QCD is a type of Quantum field theory called a non- abelian gauge theory with symmetry group SU(3). The QCD analog of electric charge is a property called 'color'. Gluons are the force carrier of the theory, like photons are for the electromagnetic force in quantum electrodynamics. The theory is an important part of the Standard Model of Particle physics. A huge body of experimental evidence for QCD has been gathered over the years. QCD enjoys two peculiar properties: Confinement, which means that the force between quarks does not diminish as they are separated. Because of this, when you do split the quark the energy is enough to create another quark thus creating another quark pair; they are forever bound into hadrons such as theproton and the neutron or the pion and kaon. Although analytically unproven, confinement is widely believed to be true because it explains the consistent failure of free quark searches, and it is easy to demonstrate in lattice QCD. Asymptotic freedom, which means that in very high-energy reactions, quarks and gluons interact very weakly creating a quark–gluon plasma. This prediction of QCD was first discovered in the early 1970s by David Politzer and by Frank Wilczek and David Gross. For this work they were awarded the 2004 Nobel Prize in Physics. There is no known phase-transition line separating these two properties; confinement is dominant in low-energy scales but, as energy increases, asymptotic freedom becomes dominant.
    [Show full text]
  • Structure of Matter
    STRUCTURE OF MATTER Discoveries and Mysteries Part 2 Rolf Landua CERN Particles Fields Electromagnetic Weak Strong 1895 - e Brownian Radio- 190 Photon motion activity 1 1905 0 Atom 191 Special relativity 0 Nucleus Quantum mechanics 192 p+ Wave / particle 0 Fermions / Bosons 193 Spin + n Fermi Beta- e Yukawa Antimatter Decay 0 π 194 μ - exchange 0 π 195 P, C, CP τ- QED violation p- 0 Particle zoo 196 νe W bosons Higgs 2 0 u d s EW unification νμ 197 GUT QCD c Colour 1975 0 τ- STANDARD MODEL SUSY 198 b ντ Superstrings g 0 W Z 199 3 generations 0 t 2000 ν mass 201 0 WEAK INTERACTION p n Electron (“Beta”) Z Z+1 Henri Becquerel (1900): Beta-radiation = electrons Two-body reaction? But electron energy/momentum is continuous: two-body two-body momentum energy W. Pauli (1930) postulate: - there is a third particle involved + + - neutral - very small or zero mass p n e 휈 - “Neutrino” (Fermi) FERMI THEORY (1934) p n Point-like interaction e 휈 Enrico Fermi W = Overlap of the four wave functions x Universal constant G -5 2 G ~ 10 / M p = “Fermi constant” FERMI: PREDICTION ABOUT NEUTRINO INTERACTIONS p n E = 1 MeV: σ = 10-43 cm2 휈 e (Range: 1020 cm ~ 100 l.yr) time Reines, Cowan (1956): Neutrino ‘beam’ from reactor Reactions prove existence of neutrinos and then ….. THE PREDICTION FAILED !! σ ‘Unitarity limit’ > 100 % probability E2 ~ 300 GeV GLASGOW REFORMULATES FERMI THEORY (1958) p n S. Glashow W(eak) boson Very short range interaction e 휈 If mass of W boson ~ 100 GeV : theory o.k.
    [Show full text]
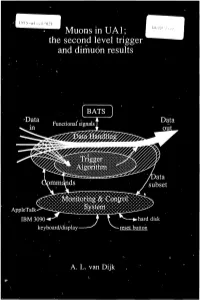
  • The Second Level Trigger and Dimuon Results
    ••~ Muonsin UA1; the second level trigger and dimuon results BATS -Data Functional signals /Data )mm; subset AppleTalk. S\S\ IBM 3090 •hard disk keyboard/display • reset button A. L. van Dijk Muons inUAl; the second level trigger and dimuon results ACADEMISCH PROEFSCHRIFT ter verkrijging van de graad van doctor aan de Universiteit van Amsterdam, op gezag van de Rector Magnificus Prof. Dr. P. W. M. de Meijer, in het openbaar te verdedigen in de Aula der Universiteit (Oude Lutherse Kerk, ingang Singel 411, hoek Spui) op dinsdag 26 februari 1991 te 15:00 uur. door Adriaan Louis van Dijk geboren te Amsterdam Promotor: Prof. Dr. J. J. Engelen Co-Promotor: Dr. K. Bos The work described in this thesis is part of the research program of the 'Nationaal Instituut voor Kernfysica en Hoge Energie Fysica (NIKHEFH)'. The author was financially supported by the 'Stichting voor Fundamenteel Onderzoek der Materie (FOM)'. Contents I Introduction 1 1.1 Proton-ontlproton physics, motivation 1 1.2 The CERN proton-antiprolon collider 2 1.3 Collider performance and physics achievements 3 1.4 Jets, muons, heavy flavours and flavour mixing S 1.5 Outline of this thesis 7 II TheUAl Experiment 8 2.1 Introduction 8 2.2 The UA1 coordinate system 10 2.3 Central detector (CD) 11 2.4 The Hadronic Calorimeter 14 2.5 Muon detection system IS 2.6 Triggering and daia acquisition (1987-1990) 18 III Data Acquisition and Triggers 20 3.1 Introduction 20 3.2 Daia acquisition 21 3.2.2 The Event Building 23 3.2.3 Hardware and standards 23 3.2.4 Software 24 3.2.5 Ergonomics 24 3.3
    [Show full text]
  • Week 3: Thermal History of the Universe
    Week 3: Thermal History of the Universe Cosmology, Ay127, Spring 2008 April 21, 2008 1 Brief Overview Before moving on, let’s review some of the high points in the history of the Universe: T 10−4 eV, t 1010 yr: today; baryons and the CMB are entirely decoupled, stars and • ∼ ∼ galaxies have been around a long time, and clusters of galaxies (gravitationally bound systems of 1000s of galaxies) are becoming common. ∼ T 10−3 eV, t 109 yr; the first stars and (small) galaxies begin to form. • ∼ ∼ T 10−1−2 eV, t millions of years: baryon drag ends; at earlier times, the baryons are still • ∼ ∼ coupled to the CMB photons, and so perturbations in the baryon cannot grow; before this time, the gas distribution in the Universe remains smooth. T eV, t 400, 000 yr: electrons and protons combine to form hydrogen atoms, and CMB • ∼ ∼ photons decouple; at earlier times, photons are tightly coupled to the baryon fluid through rapid Thomson scattering from free electrons. T 3 eV, t 10−(4−5) yrs: matter-radiation equality; at earlier times, the energy den- • ∼ ∼ sity of the Universe is dominated by radiation. Nothing really spectacular happens at this time, although perturbations in the dark-matter density can begin to grow, providing seed gravitational-potential wells for what will later become the dark-matter halos that house galaxies and clusters of galaxies. T keV, t 105 sec; photons fall out of chemical equilibrium. At earlier times, interac- • ∼ ∼ tions that can change the photon number occur rapidly compared with the expansion rate; afterwards, these reactions freeze out and CMB photons are neither created nor destroyed.
    [Show full text]
  • Supersymmetry in the Shadow of Photini
    Photini in the UV Photini in the IR Photini at the LHC Supersymmetry in the shadow of photini Ken Van Tilburg August 24, 2012 In collaboration with: Masha Baryakhtar (Stanford), Nathaniel Craig (Rutgers, IAS) Reference: arXiv:1206.0751; JHEP 1207 (2012) 164 Arvanitaki et al: arXiv:0909:5440; Phys.Rev.D81 (2010) 075018 1/6 Photini in the UV Photini in the IR Photini at the LHC Table of contents 1 Photini in the UV 2 Photini in the IR 3 Photini at the LHC 2/6 Photini in the UV Photini in the IR Photini at the LHC Photini in the UV Main features of string theory: 1 supersymmetry assume broken at low energy to solve hierarchy problem 2 extra dimensions (6) assume small size generically complex compactification manifold to get SM very simple manifold: 6-torus ! six 1- and 5-cycles, fifteen 2- and 4-cycles, twenty 3-cycles IIB string theory: 4-form gauge field integrated over 3-cycle i R ! 4D vector gauge field without charged matter Aµ = C4 Σi string theory ! SUSY SM many extra \photon" superfields without any charged matter can in principle mix with U(1) hypercharge and among each other 3/6 Photini in the UV Photini in the IR Photini at the LHC Photini in the IR in SUSY limit, no observable effect: Z 2 L ⊃ d θ WaWa + WbWb − 2WaWb shift away mixing: W ! W − W and g ! p ga b b a a 1−2 physical effects from SUSY breaking, when gauginos get mass y µ δL ⊃ zijλi iσ @µλj − mijλi λj expect sizeable number of photini to be lighter than the bino bino-photino + interphotini cascade via emissions of h; Z; γ 4/6 gluino-bino model gluino-squark-bino model drastically weakened hadronic search limits: slightly enhanced leptonic search sensitivity: Photini in the UV Photini in the IR Photini at the LHC Photini at the LHC reduction of missing ET 1.0 bino 150 GeV L .
    [Show full text]
  • Abdus Salam United Nations Educational, Scientific and Cultural Organization International XAO100669 Centre •I,'
    the IC/2000/182 abdus salam united nations educational, scientific and cultural organization international XAO100669 centre •i,' international atomic energy agency for theoretical physics " F ^9 -- •.'— -> J AXINO PRODUCTION IN e+e" AND yy COLLISIONS Hoang Ngoc Long and Dang Van Soa 32/ 17 Available at: http://www.ictp.trieste.it/~pub-off IC/2000/182 United Nations Educational Scientific and Cultural Organization and International Atomic Energy Agency THE ABDUS SALAM INTERNATIONAL CENTRE FOR THEORETICAL PHYSICS AXINO PRODUCTION IN e+e" AND 77 COLLISIONS Hoang Ngoc Long Institute of Physics, NCST, P.O. Box 429, Bo Ho, Hanoi 10000, Vietnam1 and The Abdus Salam International Centre for Theoretical Physics, Trieste, Italy and Dang Van Soa Department of Physics, Hanoi University of Mining and Geology, Dong Ngac, Tu Liem, Hanoi, Vietnam1 and The Abdus Salam International Centre for Theoretical Physics, Trieste, Italy. Abstract Production of axinos and photinos in e+e~ and 77 collisions is calculated and estimated. It is shown that there is an upper limit of the cross section for the process e~e+ —> ayc dependent only on the breaking scale. For the process 77 —> aac, there is a special direction in which axinos are mainly produced. Behaviour of cross section for this process is also analysed. Based on the result a new constraint for F/N is derived: j^ > 1014 GeV. MIRAMARE - TRIESTE December 2000 1 Permanent address. Axinos - supersymmetric partners of axions [1-3] are predicted in low-energy supersym- metry and the Peccei-Quinn (PQ) solution. The axino is an electrically and color neutral particle with mass highly dependent of the models [4-6].
    [Show full text]
  • I . .- SLAC-PUB-4497 - May 1988 T/E/AS
    I . .- SLAC-PUB-4497 - May 1988 T/E/AS BOLOMETRIC DETECTION OF COLD DARK MATTER CANDIDATES: Some Material Considerations* A. K. DRUKIER Applied Research Corporation 8201 Corporate Drive, Suite 920 Landover, MD 20785 and Physics Department University of Maryland College Park, MD 20742 and KATHERINE FREESE’ Department of Astronomy Ufliversity of California Berkeley, CA 94720 -. - and JOSHUA FRIEMAN Stanford Linear Accelerator Center Stanford University, Stanford, California 94309 Submitted to Journal of Applied Physics - * Work supported by the Department of Energy, contract DE-AC03-76SF00515. + Present address: Dept. of Physics, Massachussetts Institute of Technology, Cambridge, MA 02139 ABSTRACT We discuss the use of crystal bolometers to search for weakly interacting cold dark matter particles in the galactic halo. For particles with spin dependent nuclear interactions, such as photinos, Majorana neutrinos and higgsinos, we show that compounds of boron, lithium, or fluorine are optimal detector components. We give careful estimates of expected cross-sections and event rates and discuss optimal -. - detector granularities. 2 - 1. Introduction The rotation curves of spiral galaxies are flat out to large radii, indicating that galactic halos extend out far beyond the visible matter.’ If this dark matter is non- baryonic, as suggested by a variety of arguments: it may consist of one of several exotic candidates. Weakly interacting massive particles (WIMPS) are candidates in the GeV mass range which interact with ordinary matter with cross sections O( 10-38) cm2. WIMPS can be divided into two classes: (I) those with coherent interactions on matter, i.e., cross-sections o( N2, where N is approximately the atomic number of the scattering nucleus.
    [Show full text]