Unit 01 Homework
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Staten Island FAMILY • April 2012 Children at Play Early Intervention Center 40 Merrill Ave Staten Island, NY 10314 (718) 370-7529 [email protected]
CampSummer GuideApril 2012 STATEN ISLAND FREE Family Where Every Child Matters Kids celebrate the earth Spring around town! Festivals, concerts, shows, parties and more Find us online at www.NYParenting.com ARE YOUR VEINS IN SHAPE FOR SUMMER? GET HEALTHY, WITH A PAINLESS SCREENING. Summer is coming. Which means bathing suits, shorts and increased physical activity. Gear up with a free varicose vein screening with one of our vascular specialists. Appointments are limited. Call today. 718.226.6800. ʿЎƪ̋Ʃ̋̍ƮƱƲȀ̍ΞȚȚƯ̋Ʊ Vascular Specialists of Staten Island University Hospital Jonathan Deitch, MD FACS s Jonathan Schor, MD s Kuldeep Singh, MD RPVI VARICOSE VEIN SCREENING Free screenings from 1PM to 6PM THURSDAY APRIL 256 Mason Avenue, Building26 B, 2nd Floor CALL 718.226.6800 STATEN ISLAND Family April 2012 FEATURES 6 Earth celebration Tompkinsville hosts an interactive discovery day with emphasis on family fun BY SHAVANA AbRUZZO 12 Make a difference during Autism Awareness Month BY REBECCA MCKEE 14 Stop struggling with the juggling 28 Here are some tips on how to balance family, work, friends, and personal time, so you feel less stressed BY SANDRA GORDON 18 Homesick blues 10 ways for parents to help their little campers adjust 26 Playing it safe Tips on preventing Little League injuries BY TONY WANICH, MD 28 Big fun on a small budget Birthday parties that won’t break the bank BY CANDI SPARks 32 It can’t be easy, being a baby One dad’s thoughts on why newborns put up such a fight when trying anything new BY TIM PERRINS 32 34 Find new use for old clothes with a quilt Turn your child’s baby clothes into a family heirloom 28 BY KATHY SENA 40 Money doesn’t buy happiness COLUMNS Psychologist’s new book finds the best things in 10 Family Health life are free BY SAIDI CLEMENTE, MD BY ALLISON PLItt 16 Mommy 101 CALENDAR OF EVENTS BY ANGELICA SERADOVA 36 Ask an Attorney 45 Going Places BY ALISON ARDEN BESUNDER, EsQ. -

Monty Python Sub Ita
Monty python sub ita Seguici su Facebook: Da "Il Circo Volante dei Monty Python. Seguici su Facebook: Da. Monty Python's Flying Circus, Stagione 3, Episodio 33 "Salad days", sketch "The Cheese Shop. Fra l'altro i Monty sapevano tutti perfettamente il tedesco. Fecero anche un paio di puntate speciali. Monty Python's Flying Circus Season 3, episode 39, "Grandstand" Scusate per la spiegazione a monty python - il dipinto di picasso in bicicletta - Duration: sciscia79 12, views · · Monty Python Flying Circus (sub ita) - Timmy Williams. Monty Python's Flying Circus, Stagione 3, Episodio 36, sketch "Is there life after death. Seguici su Facebook: Da "Il Circo Volante dei Monty Python" sottotitolato in italiano. Stagione 2 Episodio 8 - "Archeo. IL CIRCO VOLANTE DEI MONTY PYTHON [SubITA]. di filmperevolvere · Pubblicato 22/04/ · Aggiornato 22/07/ Il circo volante dei Monty Python. Monty Python, Monty Python Flying Circus (sub ita) - I Disorientatori di gatti (Confuse a cat), video. Chords for Penis song/The naval medley - Monty Python live Mostly (Sub Ita). Play along with guitar, ukulele, or piano with interactive chords and diagrams. Chords for Monty Python Live At Hollywood Bowl - Bruces' Philosophers Song (Sub Ita) D#, G#, C#. E ora qualcosa di completamente diverso – Monty Python (). COMICO Monty Python e il Sacro Graal () A Liar's Autobiography [Sub-ITA] (). COMICO – DURATA 90′ – GRAN BRETGNA. Avventure e guai tragicomici di re Artù e dei suoi cavalieri che vanno alla ricerca del santo Graal e fanno gli. Day Lumberjack Song, Monty Python. Why don't I listen to this song more often? It always makes me laugh! Should remedy this issue and make a resolution. -

The Fairly Incomplete & Rather Badly
THE FAIRLY INCOMPLETE & RATHER BADLY ILLUSTRATI- > n how to play the pian Dwlgmdby Gary Marsh/Gone Loncron Wlmtmtd by Terry Gllllam, mry Ma*. John Murst Music dltod by dohn Du Pmz oue!d aql lnoqyw lnq awes aql ~s!ue!de ay!7 . pazeure aq spuay4 lnoA yaae~'S ,laplo 1aa.1.1oaaqa u! saaou aq6!1 aqa a!q Aaqa alns 6u!yeur 'anoqe s~a6u!4~noA aAoyy -p saaou aqa 40 do1 uo s.1a6u!4~noA and 'uado Al(n4 s! oue!d aqa aauo -E (Aeld a,uea noA 4! 'le!yuassa IOU) a! uado pue oue!d aqa u! a! and -Z Aay aq6!1 aqa aaalas ' c A Foreword by Elvis Presley Hi. You know, whenever I'm browsing through a shopping mall, or busy buying groceries at a supermarket, I often find myself humming one of the many happy songs that these Monty Python guys have churned out over the years. "I'm a lumberjack and I'm okay," I'll find myself crooning as I tip a grocery clerk a new pink Cadillac, or "Isn't it awfully nice to have a penis," I'll sing as I buy some more Listerine. It's amazing how often I find myself breaking into "Ya Di Bucketty", especially when the holidays come around. How I wish I could have tHat on my Christmas album. And I'd give anything to have recorded the "Bruces' Philosophers Song", instead of "All Shook Up". Listen, if you ask me these guys are the greatest, and if only I were alive today I would be covering some of their epoch-making songs. -

Music Inspired by Astronomy, Organized by Topic an Annotated Listing by Andrew Fraknoi
Music Inspired by Astronomy, Organized by Topic An Annotated Listing by Andrew Fraknoi © copyright 2019 by Andrew Fraknoi. All rights reserved. Used with permission. Borresen: At Uranienborg Cage: Atlas Eclipticalis Glass: Orion Connections between astronomy and music have been proposed since the time of the ancient Greeks. This annotated listing of both classical and popular music inspired by astronomy restricts itself to music that has connections to real science -- not just an astronomical term or two in the title or lyrics. For example, we do not list Gustav Holst’s popular symphonic suite The Planets, because it draws its inspiration from the astrological, and not astronomical, characteristics of the worlds in the solar system. Similarly, songs like Soundgarden’s “Black Hole Sun” or the Beatles’ “Across the Universe” just don’t contain enough serious astronomy to make it into our guide. When possible, we give links to a CD and a YouTube recording or explanation for each piece. The music is arranged in categories by astronomical topic, from asteroids to Venus. Additions to this list are most welcome (as long as they follow the above guidelines); please send them to the author at: fraknoi {at} fhda {dot} edu Table of Contents Asteroids Meteors and Meteorites Astronomers Moon Astronomy in General Nebulae Black Holes Physics Related to Astronomy Calendar, Time, Seasons Planets (in General) Comets Pluto Constellations Saturn Cosmology SETI (Search for Intelligent Life Out There) Earth Sky Phenomena Eclipses Space Travel Einstein Star Clusters Exoplanets Stars and Stellar Evolution Galaxies and Quasars Sun History of Astronomy Telescopes and Observatories Jupiter Venus Mars 1 Asteroids Coates, Gloria Among the Asteroids on At Midnight (on Tzadik). -

Galaxy Song, the Artist:Monty Python , Writer: Eric Idle and John Du Prez
Galaxy Song, The artist:Monty Python , writer: Eric Idle and John Du Prez Thanks to Ian Blackhouse for this one !! https://www.youtube.com/watch?v=buqtdpuZxvk Capo 4 [D7] Just re-[G]-member that you're standing on a planet that's evolving revolving at nine hundred miles an [D7] hour [D7] And orbiting at nineteen miles a second, so it's reckoned A sun that is the source of all our [G] power [G] The sun and you and me, and all the stars that we can see Are [E7] moving at a million miles a [C] day In an [Gdim] outer spiral arm, at forty [G] thousand miles an hour Of the [D7] galaxy we call the Milky [G] Way [D7] [G] [G] Our galaxy itself contains a hundred billion stars It's a hundred thousand light-years side-to-[D7]-side [D7] It bulges in the middle, sixteen thousand light-years thick But out by us it's just three thousand light-years [G] wide [G] We're thirty thousand light-years from galactic central point We go [E7] round eve-ry two hundred million [C] years And our [Gdim] galaxy itself is one of [G] millions of billions In this [D7] amazing and expanding uni-[G]-verse [D7] [G] [G] The universe itself keeps on expanding and expanding In all of the directions it can [D7] whiz [D7] As fast as it can go, at the speed of light you know Twelve million miles a minute and that's the [G] fastest speed there is [G] So remember, when you're feeling very small and insecure How [E7] amazingly unlikely is your [C] birth And [Gdim] pray that there's intelligent life [G] somewhere up in space Because there's [D7] bugger all down here on [G] Earth [D7] [G] Produced by www.ozbcoz.com - Jim's Guitar Songbook Guitar Tuning EADGBE. -

Songs by Artist
Sound Master Entertianment Songs by Artist smedenver.com Title Title Title .38 Special 2Pac 4 Him Caught Up In You California Love (Original Version) For Future Generations Hold On Loosely Changes 4 Non Blondes If I'd Been The One Dear Mama What's Up Rockin' Onto The Night Thugz Mansion 4 P.M. Second Chance Until The End Of Time Lay Down Your Love Wild Eyed Southern Boys 2Pac & Eminem Sukiyaki 10 Years One Day At A Time 4 Runner Beautiful 2Pac & Notorious B.I.G. Cain's Blood Through The Iris Runnin' Ripples 100 Proof Aged In Soul 3 Doors Down That Was Him (This Is Now) Somebody's Been Sleeping Away From The Sun 4 Seasons 10000 Maniacs Be Like That Rag Doll Because The Night Citizen Soldier 42nd Street Candy Everybody Wants Duck & Run 42nd Street More Than This Here Without You Lullaby Of Broadway These Are Days It's Not My Time We're In The Money Trouble Me Kryptonite 5 Stairsteps 10CC Landing In London Ooh Child Let Me Be Myself I'm Not In Love 50 Cent We Do For Love Let Me Go 21 Questions 112 Loser Disco Inferno Come See Me Road I'm On When I'm Gone In Da Club Dance With Me P.I.M.P. It's Over Now When You're Young 3 Of Hearts Wanksta Only You What Up Gangsta Arizona Rain Peaches & Cream Window Shopper Love Is Enough Right Here For You 50 Cent & Eminem 112 & Ludacris 30 Seconds To Mars Patiently Waiting Kill Hot & Wet 50 Cent & Nate Dogg 112 & Super Cat 311 21 Questions All Mixed Up Na Na Na 50 Cent & Olivia 12 Gauge Amber Beyond The Grey Sky Best Friend Dunkie Butt 5th Dimension 12 Stones Creatures (For A While) Down Aquarius (Let The Sun Shine In) Far Away First Straw AquariusLet The Sun Shine In 1910 Fruitgum Co. -

Songs by Artist
Songs by Artist Title Title (Hed) Planet Earth 2 Live Crew Bartender We Want Some Pussy Blackout 2 Pistols Other Side She Got It +44 You Know Me When Your Heart Stops Beating 20 Fingers 10 Years Short Dick Man Beautiful 21 Demands Through The Iris Give Me A Minute Wasteland 3 Doors Down 10,000 Maniacs Away From The Sun Because The Night Be Like That Candy Everybody Wants Behind Those Eyes More Than This Better Life, The These Are The Days Citizen Soldier Trouble Me Duck & Run 100 Proof Aged In Soul Every Time You Go Somebody's Been Sleeping Here By Me 10CC Here Without You I'm Not In Love It's Not My Time Things We Do For Love, The Kryptonite 112 Landing In London Come See Me Let Me Be Myself Cupid Let Me Go Dance With Me Live For Today Hot & Wet Loser It's Over Now Road I'm On, The Na Na Na So I Need You Peaches & Cream Train Right Here For You When I'm Gone U Already Know When You're Young 12 Gauge 3 Of Hearts Dunkie Butt Arizona Rain 12 Stones Love Is Enough Far Away 30 Seconds To Mars Way I Fell, The Closer To The Edge We Are One Kill, The 1910 Fruitgum Co. Kings And Queens 1, 2, 3 Red Light This Is War Simon Says Up In The Air (Explicit) 2 Chainz Yesterday Birthday Song (Explicit) 311 I'm Different (Explicit) All Mixed Up Spend It Amber 2 Live Crew Beyond The Grey Sky Doo Wah Diddy Creatures (For A While) Me So Horny Don't Tread On Me Song List Generator® Printed 5/12/2021 Page 1 of 334 Licensed to Chris Avis Songs by Artist Title Title 311 4Him First Straw Sacred Hideaway Hey You Where There Is Faith I'll Be Here Awhile Who You Are Love Song 5 Stairsteps, The You Wouldn't Believe O-O-H Child 38 Special 50 Cent Back Where You Belong 21 Questions Caught Up In You Baby By Me Hold On Loosely Best Friend If I'd Been The One Candy Shop Rockin' Into The Night Disco Inferno Second Chance Hustler's Ambition Teacher, Teacher If I Can't Wild-Eyed Southern Boys In Da Club 3LW Just A Lil' Bit I Do (Wanna Get Close To You) Outlaw No More (Baby I'ma Do Right) Outta Control Playas Gon' Play Outta Control (Remix Version) 3OH!3 P.I.M.P. -

Monty Python's Completely Useless Web Site
Home Get Files From: ● MP's Flying Circus ● Completely Diff. ● Holy Grail ● Life of Brian ● Hollywood Bowl ● Meaning of Life General Information | Monty Python's Flying Circus | Monty Python and the Holy Grail | Monty Python's Life of Brian | Monty Python Live at the Hollywood Bowl | Monty Python's The Meaning of Life | Monty Python's Songs | Monty Python's Albums | Monty Python's ...or jump right to: Books ● Pictures ● Sounds ● Video General Information ● Scripts ● The Monty Python FAQ (25 Kb) Other stuff: ● Monty Python Store ● Forums RETURN TO TOP ● About Monty Python's Flying Circus Search Now: ● Episode Guide (18 Kb) ● The Man Who Speaks In Anagrams ● The Architects ● Argument Sketch ● Banter Sketch ● Bicycle Repair Man ● Buying a Bed ● Blackmail ● Dead Bishop ● The Man With Three Buttocks ● Burying The Cat ● The Cheese Shoppe ● Interview With Sir Edward Ross ● The Cycling Tour (42 Kb) ● Dennis Moore ● The Hairdressers' Ascent up Mount Everest ● Self-defense Against Fresh Fruit ● The Hospital ● Johann Gambolputty... ● The Lumberjack Song [SONG] ● The North Minehead Bye-Election ● The Money Programme ● The Money Song [SONG] ● The News For Parrots ● Penguin On The Television ● The Hungarian Phrasebook ● Flying Sheep ● The Pet Shop ● The Tale Of The Piranha Brothers (10 Kb) ● String ● A Pet Shop Near Melton Mowbray ● The Trail ● Arthur 'Two Sheds' Jackson ● The Woody Sketch ● 1972 German Special (42 Kb) RETURN TO TOP Monty Python and the Holy Grail ● Complete Script Version 1 (74 Kb) ● Complete Script Version 2 (195 Kb) ● The Album Of -

1 Amazing Grace
1Amazing Grace BY JOHN NEWTON 1. Amazing grace, how sweet the sound That saves a wretch like me. I once was lost, but now I'm found; Was bound, but now I’m free. 2. 'Twas grace that taught my heart to fear And grace my fear relieved; How precious did that grace appear The hour I first believed. 3. Through many dangers, toils and snares We have already come; 'Twas grace that brought us safe thus far, And grace will lead us on. 4. When we've been there ten thousand years, Bright shining as the sun, We've no less days to sing God's praise Than when we’d first begun. 5. Amazing grace, how sweet the sound That saves a wretch like me. I once was lost, but now I'm found; Was bound, but now I'm free. 2Just aCloser Walk With Thee TRADITIONAL 1. Just a closer walk with Thee, Grant it, Jesus, is my plea; Daily walking close with Thee, Let it be, dear Lord, let it be. 2. Through the days of toil and snares, If I falter, Lord, who cares? Who with me my burden shares? None but Thee, dear Lord, none but Thee. 3. When my feeble life is o'er Time for me will be no more; Guide me gently, safely on To thy shore, dear Lord, to thy shore. 4. I am weak, but Thou art strong. Jesus, keep me from all wrong. I'll be satisfied as long As I walk, let me walk close to Thee. -
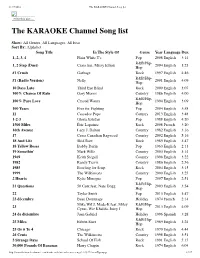
The KARAOKE Channel Song List
11/17/2016 The KARAOKE Channel Song list Print this List ... The KARAOKE Channel Song list Show: All Genres, All Languages, All Eras Sort By: Alphabet Song Title In The Style Of Genre Year Language Dur. 1, 2, 3, 4 Plain White T's Pop 2008 English 3:14 R&B/Hip- 1, 2 Step (Duet) Ciara feat. Missy Elliott 2004 English 3:23 Hop #1 Crush Garbage Rock 1997 English 4:46 R&B/Hip- #1 (Radio Version) Nelly 2001 English 4:09 Hop 10 Days Late Third Eye Blind Rock 2000 English 3:07 100% Chance Of Rain Gary Morris Country 1986 English 4:00 R&B/Hip- 100% Pure Love Crystal Waters 1994 English 3:09 Hop 100 Years Five for Fighting Pop 2004 English 3:58 11 Cassadee Pope Country 2013 English 3:48 1-2-3 Gloria Estefan Pop 1988 English 4:20 1500 Miles Éric Lapointe Rock 2008 French 3:20 16th Avenue Lacy J. Dalton Country 1982 English 3:16 17 Cross Canadian Ragweed Country 2002 English 5:16 18 And Life Skid Row Rock 1989 English 3:47 18 Yellow Roses Bobby Darin Pop 1963 English 2:13 19 Somethin' Mark Wills Country 2003 English 3:14 1969 Keith Stegall Country 1996 English 3:22 1982 Randy Travis Country 1986 English 2:56 1985 Bowling for Soup Rock 2004 English 3:15 1999 The Wilkinsons Country 2000 English 3:25 2 Hearts Kylie Minogue Pop 2007 English 2:51 R&B/Hip- 21 Questions 50 Cent feat. Nate Dogg 2003 English 3:54 Hop 22 Taylor Swift Pop 2013 English 3:47 23 décembre Beau Dommage Holiday 1974 French 2:14 Mike WiLL Made-It feat. -
![Arxiv:1908.07026V1 [Cs.LG] 19 Aug 2019 to Opnn,Ie,Tedcdr Upt Sum- Outputs Decoder, the I.E., Component, Ation E Tal](https://docslib.b-cdn.net/cover/4729/arxiv-1908-07026v1-cs-lg-19-aug-2019-to-opnn-ie-tedcdr-upt-sum-outputs-decoder-the-i-e-component-ation-e-tal-3124729.webp)
Arxiv:1908.07026V1 [Cs.LG] 19 Aug 2019 to Opnn,Ie,Tedcdr Upt Sum- Outputs Decoder, the I.E., Component, Ation E Tal
Topic Augmented Generator for Abstractive Summarization Melissa Ailem1, Bowen Zhang1 and Fei Sha1,2 1 University of Southern California, Los Angeles, CA 1 {ailem, zhan734, feisha}@usc.edu 2 [email protected] Abstract mary by conditioning on the input text (and its rep- resentation through the encoder). Steady progress has been made in abstractive What kind of information can we introduce so summarization with attention-based sequence- that richer texts can appear in the summaries? In to-sequence learning models. In this paper, we propose a new decoder where the output sum- this paper, we describe how to combine topic mod- mary is generated by conditioning on both the eling with models for abstractive summarization. input text and the latent topics of the docu- Topics identified from topic modeling, such as La- ment. The latent topics, identified by a topic tent Dirichlet Allocation (LDA), capture corpus- model such as LDA, reveals more global se- level patterns of words co-occurrence and describe mantic information that can be used to bias documents with mixtures of semantically coher- the decoder to generate words. In particular, ent conceptual groups. Such usages of words and they enable the decoder to have access to ad- ditional word co-occurrence statistics captured concepts provide valuable inductive bias for super- at document corpus level. We empirically vali- vised models for language generation. date the advantage of the proposed approach We propose Topic Augmented Generator (TAG) on both the CNN/Daily Mail and the Wiki- for abstractive summarization where the popular How datasets. Concretely, we attain strongly pointer-generator based decoder is supplied with improved ROUGE scores when compared to latent topics of the input document (See et al., state-of-the-art models. -

Absurdity and Irony in the Work of Monty Python
Univerzita Hradec Králové Pedagogická fakulta Katedra anglického jazyka a literatury Absurdity and Irony in the Work of Monty Python Bakalářská práce Autor: Barbora Štěpánová Studijní program: B 7310 Filologie Studijní obor: P-AJCRB Cizí jazyky pro cestovní ruch – anglický jazyk P-NJCRB Cizí jazyky pro cestovní ruch – německý jazyk Vedoucí práce: Mgr. Jan Suk Hradec Králové 2016 Prohlášení Prohlašuji, že jsem tuto bakalářskou práci vypracovala (pod vedením vedoucího bakalářské práce) samostatně a uvedla jsem všechny pouţité prameny a literaturu. V Hradci Králové dne … Poděkování Ráda bych touto cestou vyjádřila poděkování Mgr. Janu Sukovi za jeho vstřícnost, trpělivost a za cenné rady při vedení bakalářské práce. Anotace ŠTĚPÁNOVÁ, Barbora. Absurdita a ironie v díle skupiny Monty Python. Hradec Králové: Pedagogická fakulta Univerzity Hradec Králové, 2016. 46 s. Bakalářská práce. Cílem bakalářské práce je poukázat na prvky absurdity a ironie v díle britské humoristické skupiny Monty Python. Tyto elementy budou nastíněny analýzou jejich televizní a filmové tvorby. Dále předkládaná studie podtrhuje elementy "montypythonovského" humoru v kontextu tradičního pojetí humoru. V neposlední řadě bakalářská práce představuje jednotlivé členy této skupiny, seznamuje s jejich dílem jako takovým a všímá si jejich vlivu na další vývoj britské komedie. Klíčová slova: absurdita, ironie, britský humor, Monty Python. Annotation ŠTĚPÁNOVÁ, Barbora. Absurdity and Irony in the Work of Monty Python. Hradec Králové: Pedagogická fakulta Univerzity Hradec Králové, 2016. 46 p. Bachelor Degree Thesis. The goal of the bachelor's thesis is to point out the elements of absurdity and irony in the work of the British comedy group Monty Python. These elements will be demonstrated by the analysis of the television and film production of the group.