A Comparative Study of Marks in Some Connecticut Valley High Schools with Enrollment Over 100 James Bower University of Massachusetts Amherst
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
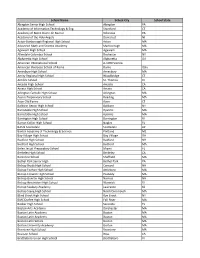
Participating School List 2018-2019
School Name School City School State Abington Senior High School Abington PA Academy of Information Technology & Eng. Stamford CT Academy of Notre Dame de Namur Villanova PA Academy of the Holy Angels Demarest NJ Acton-Boxborough Regional High School Acton MA Advanced Math and Science Academy Marlborough MA Agawam High School Agawam MA Allendale Columbia School Rochester NY Alpharetta High School Alpharetta GA American International School A-1090 Vienna American Overseas School of Rome Rome Italy Amesbury High School Amesbury MA Amity Regional High School Woodbridge CT Antilles School St. Thomas VI Arcadia High School Arcadia CA Arcata High School Arcata CA Arlington Catholic High School Arlington MA Austin Preparatory School Reading MA Avon Old Farms Avon CT Baldwin Senior High School Baldwin NY Barnstable High School Hyannis MA Barnstable High School Hyannis MA Barrington High School Barrington RI Barron Collier High School Naples FL BASIS Scottsdale Scottsdale AZ Baxter Academy of Technology & Science Portland ME Bay Village High School Bay Village OH Bedford High School Bedford NH Bedford High School Bedford MA Belen Jesuit Preparatory School Miami FL Berkeley High School Berkeley CA Berkshire School Sheffield MA Bethel Park Senior High Bethel Park PA Bishop Brady High School Concord NH Bishop Feehan High School Attleboro MA Bishop Fenwick High School Peabody MA Bishop Guertin High School Nashua NH Bishop Hendricken High School Warwick RI Bishop Seabury Academy Lawrence KS Bishop Stang High School North Dartmouth MA Blind Brook High -

Annual Report
HUMAN CAPITAL FISCAL YEAR 2019 ANNUAL REPORT INNOVATION CAPITAL GROWTH CAPITAL INTELLECTUAL CAPITAL The capital of scientific revolution. Fiscal Year 2019 Annual Report • Massachusetts Life Sciences Center • i BOARD OF DIRECTORS TABLE OF CONTENTS A LETTER FROM THE INTERIM PRESIDENT & CEO Michael J. Heffernan Co-Chair; Secretary, Executive Office for Administration & Finance A Letter from the President & CEO ...........................................................................................1 Mike Kennealy Co-Chair; Secretary, Executive Office Vision & Strategy: The Capital of Scientific Revolution ......................................................2 The Patients Are Waiting of Housing & Economic Development Fiscal Year 2019 Highlights and The Bottom Line ..............................................................3 Gary P. Kearney, MD Around the globe, billions of patients and their loved ones await advances in health President, Longwood Urological Associates Human Capital care that will produce the products, devices, and therapies to alleviate suffering, Marty Meehan Internship Challenge: Enhancing Career Exploration improve treatment, and save lives. Much of that attention falls on Massachusetts, as President, University of Massachusetts and Expanding the Talent Pipeline ............................................................................................4 the world looks to our ecosystem to deliver the breakthroughs that further unlock our Peter Parker understanding of human physiology, harness the power of data science, -

Sanctioned Cheer Teams - 2018-19 Activity SCHOOL Mailcity Coed Fall Cheer Abington High School Abington Acton-Boxborough Reg H.S
Sanctioned Cheer Teams - 2018-19 Activity SCHOOL MailCITY Coed Fall Cheer Abington High School Abington Acton-Boxborough Reg H.S. Acton Agawam High School Agawam Algonquin Reg. High School Northborough Amesbury High School Amesbury Andover High School Andover Apponequet Regional H.S. Lakeville Archbishop Williams High School Braintree Arlington High School Arlington Ashland High School Ashland Assabet Valley Reg Tech HS Marlboro Attleboro High School Attleboro Auburn High School Auburn Austin Preparatory School Reading Barnstable High School Hyannis Bartlett Jr./Sr. H.S. Webster Bay Path RVT High School Charlton Bedford High School Bedford Bellingham High School Bellingham Belmont High School Belmont Beverly High School Beverly Billerica Memorial High School Billerica Bishop Feehan High School Attleboro Blackstone-Millville Reg HS Blackstone Boston Latin School Boston Braintree High School Braintree Bridgewater-Raynham Reg High School Bridgewater Bristol-Plymouth Reg Voc Tech Taunton Brookline High School Brookline Burlington High School Burlington Canton High School Canton Carver Middle/High School Carver Central Catholic High School Lawrence Chelmsford High School North Chelmsford Chicopee Comprehensive HS Chicopee Clinton High School Clinton Cohasset Middle-High School Cohasset Concord-Carlisle High School Concord Tuesday, January 22, 2019 Sanctioned Cheer Teams - 2018-19 Activity SCHOOL MailCITY Coed Fall Cheer Coyle & Cassidy High School Taunton Danvers High School Danvers Dartmouth High School South Dartmouth David Prouty High School -

Sanctioned Cheer Teams
Sanctioned Cheer Teams - 2010-2011 Activity SCHOOL MailCITY Coed Cheer Abby Kelley Foster Reg Charter School Worcester Abington High School Abington Academy of Notre Dame Tyngsboro Acton-Boxborough Reg H.S. Acton Agawam High School Agawam Algonquin Reg. High School Northborough Amesbury High School Amesbury Andover High School Andover Apponequet Regional H.S. Lakeville Archbishop Williams High School Braintree Arlington Catholic High School Arlington Arlington High School Arlington Ashland High School Ashland Assabet Valley Reg Voc HS Marlboro Attleboro High School Attleboro Auburn High School Auburn Auburn Middle School Auburn Austin Preparatory School Reading Avon Mid/High School Avon Ayer Middle-High School Ayer Barnstable High School Hyannis Bartlett Jr./Sr. H.S. Webster Bay Path RVT High School Charlton Bedford High School Bedford Belchertown High School Belchertown Bellingham High School Bellingham Beverly High School Beverly Billerica Memorial High School Billerica Bishop Feehan High School Attleboro Bishop Fenwick High School Peabody Bishop Stang High School North Dartmouth Blackstone Valley Reg Voc/Tech HS Upton Blackstone-Millville Reg HS Blackstone Boston Latin School Boston Bourne High School Bourne Braintree High School Braintree Bridgewater-Raynham Reg High School Bridgewater Bristol-Plymouth Reg Voc Tech Taunton Thursday, February 03, 2011 Page 1 of 7 Sanctioned Cheer Teams - 2010-2011 Activity SCHOOL MailCITY Coed Cheer Brockton High School Brockton Brookline High School Brookline Burlington High School Burlington Cambridge -

Full List of Our Partners
signal success Be career ready. Community Partners ABCD MassHire Berkshire Workforce New Directions, Inc. Associates for Human Services/Taunton Development Board New England Business Associates Area School to Career MassHire Bristol Career Center (NEBA) Atlantis Charter School MassHire Bristol Workforce Board New England Farm Workers Council Boston Private Industry Council MassHire Cape & Islands Workforce Board (NEFWC) Boston Youth Engagement and MassHire Central Region Workforce Board Partnership for A Skilled Workforce Employment MassHire Franklin Hampshire Career Center Phoenix Indian Center Boys & Girls Club of New Bedford MassHire Greater Brockton Career Center Polis Center for Social & Economic Chelsea Collaborative MassHire Greater Brockton Workforce Board Development City of Boston, Jobs & Community MassHire Greater New Bedford Career Center Project Right Service MassHire Greater New Bedford Workforce Safe & Successful Youth Initiatives City of Cambridge Board (SSYI) City of Malden MassHire Greater Lowell Career Center Seven Hills City of Phoenix Workforce Innovation & MassHire Hampden County Workforce Board Sociedad Latina Opportunity Act MassHire Holyoke Career Center The Arc Center of Hope Foundation City of Providence MassHire Merrimack Valley Career Center The Home for Little Wanderers Community Action Pioneer Valley MassHire Merrimack Valley Workforce Board Tempo Young Adult Resource Center Dorchester Youth Collaborative MassHire Metro North Workforce Board Urban League of Eastern Gateway to College MassHire Metro South/West -

PVIAC Distinguished Service Past Award Winners
PVIAC Distinguished Service Past Award Winners 2001 Charles Kimball, Principal—South Hadley High School Michael Kane-Principal—Monson High School 2002 William Decker, Principal—Frontier Regional High School Joseph Spadafora—Athletic Director—Mahar Regional High School 2003 John Domaingue, Athletic Director—West Springfield High School Andy Kozikowski, Athletic Director—Monson High School 2004 Robert Delisle, Principal-West Springfield High School Barbara Martino, Athletic Director-Holyoke Public Schools Michael Dorunda, Assistant Principal-Hampshire Regional High School 2005 James Cokkinias, Principal-Ludlow High School 2006 James Cavallo, Principal-Ludlow High School Paul Cournoyer, Athletic Director-Turners Falls High School 2007 William Mahoney, Principal-Hopkins Academy Jeff Boudway, Athletic Director-Northampton High School Al Nummy, Athletic Director- Westfield High School 2008 James Vincent, Principal-Southwick Tolland Regional High School Jeff Fisk, Athletic Director-Gateway Regional High School 2009 Michael Deary, Athletic Director-Longmeadow High School 2010 Jim Peters, Principal - Monson High School Lou Conte, Athletic Director - Agawam High School Ned Doyle, Athletic Director - Minnechaug Regional High School 2011 Nancy Kurty - Athletic Director, Ludlow High School Sherry Webb,- Athletic Director, Smith Academy Robert Englehardt - Athletic Director, Pioneer Valley Regional High School 2012 Thomas Russo – Athletic Director, Springfield Public Schools Roland Joyal, Principal – Chicopee High School 2013 Peter Dufresne, Principal – West Springfield and Granby Jr.-Sr. High Schools 2014 Donna Woodcock, Principal – Greenfield High School 2016 Ann Trytko, Athletic Director - Hampshire Regional High School 2017 Steve Lemanski, Principal - Agawam High School 2018 Don Irzyk, Athletic Director – Palmer High School 2019 Andrew Linkenhoker, Superintendent – Smith Vocational and Agricultural High School 2020 Marty Sanderson, Athletic Director - Frontier Regional High School . -

Jan2016@Scale Reportv5
I. Basic Information 2015 Annual @Scale Report for The Life Sciences Education Program from Contact: Dr. Michelle Mischke, Director of Biotechnology Education Programs Massachusetts Biotechnology Education Foundation (MassBioEd) 300 Technology Square, Eighth Floor Cambridge, MA 02139 e: [email protected] p: 617-674-5153 f: 617-674-5101 Form 1: @Scale Narrative II. Goals & Objectives Experience suggests that science and math education determines our state’s and nation’s capacity to innovate. These academic disciples are at the core of our ability to develop critical new science, technology and medicines that benefit people worldwide. While there are many factors that influence students’ interest and attitudes towards science, hands-on activities have been shown to improve students’ science learning and achievement, as well as their attitudes towards science. Students that experience scientific content first-hand through inquiry-based activities demonstrate greater learning and curiosity about the topic. As noted in America's Lab Report: Investigations in High School Science (National Academy Press, 2005), educators recogniZe the importance of laboratory experiences, but most are unprepared to lead such activities. Implementing an authentic lab-based activity is a demanding task requiring teachers to have sophisticated knowledge of science content and process, an understanding of how students learn science, the ability to asses student learning, and the skill to design instruction to support the multiple goals of science education. -
Volleyball Statewide Alignment Proposal ‐ 5 Divisions with Divisional Adjustments for Approved Alignment Appeals
GIRLS VOLLEYBALL STATEWIDE ALIGNMENT PROPOSAL ‐ 5 DIVISIONS WITH DIVISIONAL ADJUSTMENTS FOR APPROVED ALIGNMENT APPEALS Voc Coop Enrollment School Private Team NEW DIV Old Old School for (down 2 School (up 1 FOR TEAM Aligned School MailCITY Section Division Coop HostSchool Enrollmnt Alignment div) (up 1 div) Div) STATEWIDE Acton‐Boxborough Reg H.S. Acton‐Boxborough Reg H.S. Acton CW 1 1809 1809 1 Algonquin Reg. High School Algonquin Reg. High School Northborough CW 1 1395 1395 1 Andover High School Andover High School Andover N 1 1761 1761 1 Arlington High School Arlington High School Arlington CE 1 1417 1417 1 Attleboro High School Attleboro High School Attleboro S 1 1754 1754 1 Barnstable High School Barnstable High School Hyannis S 1 1530 1530 1 Belmont High School Belmont High School Belmont CE 1 1324 1324 1 Beverly High School Beverly High School Beverly N 1 1296 1296 1 Bishop Feehan High School Bishop Feehan High School Attleboro S 1 1084 1084 1 1 Boston Latin School Boston Latin School Boston CE 1 1650 1650 1 Braintree High School Braintree High School Braintree S 1 1720 1720 1 Bridgewater‐Raynham Reg High School Bridgewater‐Raynham Reg High School Bridgewater S 1 1383 1383 1 Brockton High School Brockton High School Brockton S 1 4061 4061 1 Brookline High School Brookline High School Brookline CE 1 2073 2073 1 Cambridge Rindge & Latin Schl. Cambridge Rindge & Latin Schl. Cambridge CE 1 1981 1981 1 Central Catholic High School Central Catholic High School Lawrence N 1 1180 1180 1 1 Chelmsford High School Chelmsford High School North -

2021-2022 Soccer-Boys
BOYS SOCCER STATEWIDE ALIGNMENT PROPOSAL ‐ 5 DIVISIONS WITH DIVISIONAL ADJUSTMENTS FOR APPROVED ALIGNMENT APPEALS Coop Voc School Private Team NEW DIV Old Old School Enrollment (down 2 School (up 1 FOR TEAM Aligned School MailCITY Section Division Coop HostSchool Enrollmnt for Alignment div) (up 1 div) Div) STATEWIDE Acton‐Boxborough Reg H.S. Acton‐Boxborough Reg H.S. Acton N 1 1809 1809 1 Algonquin Reg. High School Algonquin Reg. High School Northborough C 1 1395 1395 1 Andover High School Andover High School Andover N 1 1761 1761 1 Arlington High School Arlington High School Arlington N 2 1417 1417 1 Attleboro High School Attleboro High School Attleboro S 1 1754 1754 1 Barnstable High School Barnstable High School Hyannis S 1 1530 1530 1 Belmont High School Belmont High School Belmont N 2 1324 1324 1 Beverly High School Beverly High School Beverly N 2 1296 1296 1 Bishop Feehan High School Bishop Feehan High School Attleboro S 2 1084 1084 1 1 Boston College High School Boston College High School Boston S 1 1160 2320 1 1 Boston Latin School Boston Latin School Boston N 1 1650 1650 1 Braintree High School Braintree High School Braintree S 1 1720 1720 1 Bridgewater‐Raynham Reg High School Bridgewater‐Raynham Reg High School Bridgewater S 1 1383 1383 1 Brockton High School Brockton High School Brockton S 1 4061 4061 1 Brookline High School Brookline High School Brookline N 1 2073 2073 1 Cambridge Rindge & Latin Schl. Cambridge Rindge & Latin Schl. Cambridge N 1 1981 1981 1 Catholic Memorial School Catholic Memorial School West Roxbury S -

2018 MSAA Leadership Document Officers and Committees For
2017 ~ 2018 MSAA Leadership Document Officers and Committees For terms August 1, 2017 through July 31, 2018 The Board of Directors shall consist of the Executive Director, President, First Vice President, Second Vice President, Third Vice President, eight Members-At-Large (2017-2018 only), three immediate Past Presidents, the NASSP Coordinator, NAESP Coordinator and the Chairs of the respective standing committees. BOARD OF DIRECTORS Mr. Mark Wood, President Tantasqua RVHS Principal Mr. John Buckey, 1st V. P. Nantucket High School Principal Ms. Kathleen Duff, 2nd V.P. Newton Public Schools Director CTE Ms. Julie Vincentsen, 3rd V.P. Ruggles Lane Elementary School (Barre) Principal Mr. Christopher Barrett, At Large Everett High School Vice Principal Mr. Philip Conrad, At Large Andover High School Principal Mr. Peter Cushing, At Large Narraganset Middle School Principal Ms. Liz Garden, At Large Florence Roche Elementary School (Groton) Principal Ms. Maureen Kemmett, At Large Furnace Brook Middle School (Marshfield) Principal Mr. David Keim, At Large Miller Intermediate Elementary School (Holliston) Principal Mr. Henry Turner, At Large Newton North High School Principal Ms. Christine Vigneux, At Large Belchertown High School Principal Ms. Tara Bennett, Past President Millbury Jr./Sr. High School Principal Mr. George Ferro, Past President Whitman Middle School Principal Ms. Ann Knell, Past President Mattacheese Middle School Principal Mr. John Quinn, NAESP Coordinator Roosevelt Ave Elementary School (N. Attleboro) Principal Mr. Daniel Richards, NASSP State Nat’l Coord. Belmont High School Principal CHAIRS OF THE STANDING COMMITTEES Dr. Pauline Camara (Teaching and Learning) Somerset Middle School Mr. Thomas Cavanaugh (Legislative) Blue Hills Regional Tech School Mr. -

Cheer Alignments ‐ 2021‐2022 Through 2024‐2025 School Year
Cheer Alignments ‐ 2021‐2022 through 2024‐2025 School Year SCHOOL MailCITY Section Division Wachusett Regional High School Holden C 1 Shrewsbury High School Shrewsbury C 1 Leominster High School Leominster C 1 Algonquin Reg. High School Northborough C 1 Montachusett RVT High School Fitchburg C 1 Blackstone Valley Reg Voc/Tech HS Upton C 1 South High Community School Worcester C 1 Fitchburg High School Fitchburg C 1 Tantasqua Regional Senior High School Fiskdale C 1 Shepherd Hill Regional HS Dudley C 1 Nashoba Reg. High School Bolton C 1 Westborough High School Westborough C 1 Marlborough High School Marlborough C 1 Assabet Valley Reg Tech HS Marlboro C 2 Bay Path RVT High School Charlton C 2 North Middlesex Regional HS Townsend C 2 Grafton High School Grafton C 2 Quabbin Regional High School Barre C 2 Auburn High School Auburn C 2 Hudson High School Hudson C 2 Oakmont Regional High School Ashburnham C 2 Nipmuc Regional High School Upton C 2 Keefe Technical HS Framingham C 2 Nashoba Valley Technical High School Westford C 2 Northbridge High School Whitinsville C 2 Holy Name Central Catholic HS Worcester C 3 Gardner High School Gardner C 3 Uxbridge High School Uxbridge C 3 Tyngsborough High School Tyngsborough C 3 Southbridge Middle/High School Southbridge C 3 Blackstone‐Millville Reg. HS Blackstone C 3 Littleton High School Littleton C 3 Leicester High School Leicester C 3 Bartlett Jr./Sr. H.S. Webster C 3 Sutton High School Sutton C 3 Clinton High School Clinton C 3 Douglas High School Douglas C 4 Ayer Shirley Regional High School Ayer C 4 David Prouty High School Spencer C 4 Narragansett Reg. -

Winter Cooperative Teams 9/24/2021 11:51:47 Am
UPDATED: WINTER COOPERATIVE TEAMS 9/24/2021 11:51:47 AM Basketball - Boys DISTRICT APPROVAL Host School Guest School(s) 21-22 22-23 District Date Rec'd Sect/Div Bethany Christian Academy Mendon Notre Dame Prep School 3 9/24/2020 C - 4 Gymnastics - Boys DISTRICT APPROVAL Host School Guest School(s) 21-22 22-23 District Date Rec'd Sect/Div Newton North High School Newtonville Newton South High School 7 9/24/2021 X - 1 Gymnastics - Girls DISTRICT APPROVAL Host School Guest School(s) 21-22 22-23 District Date Rec'd Sect/Div Brockton High School Brockton Cardinal Spellman High School East Bridgewater Jr/Sr High School 8 12/14/2020 S - 1 Brookline High School Brookline Westwood High School 7 12/10/2020 S - 1 Danvers High School Danvers North Reading High School 5 9/24/2020 N - 1 Gloucester High School Gloucester Ipswich High School 5 12/2/2020 N - 1 Groton-Dunstable Reg. High School Groton North Middlesex Regional HS Concord-Carlisle High School 3 12/10/2020 S - 1 Littleton High School Hamilton-Wenham Reg HS South Hamilton Manchester Essex Reg. High School 5 12/2/2020 N - 1 Marblehead High School Marblehead Swampscott High School 5 9/24/2021 N - 1 Marlborough High School Marlborough Nashoba Reg. High School 3 12/10/2020 S - 1 Medfield High School Medfield Dover-Sherborn High School Ashland High School 7 12/3/2020 S - 1 Medway High School Medway Millis High School Holliston High School 7 12/14/2020 S - 1 Milford High School Plymouth North High School Plymouth Plymouth South High School 9 12/10/2020 S - 1 Westborough High School Westborough Hopkinton High School 3 9/24/2021 S - 1 Ice Hockey - Boys DISTRICT APPROVAL Host School Guest School(s) 21-22 22-23 District Date Rec'd Sect/Div Amherst-Pelham Reg High School Amherst Hopkins Academy Palmer High School 1 6/18/2021 W - 3A Apponequet Regional H.S.