Boolean Algebra and Logic Design Page 1 of 3
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Advanced Discrete Mathematics Mm-504 &
1 ADVANCED DISCRETE MATHEMATICS M.A./M.Sc. Mathematics (Final) MM-504 & 505 (Option-P3) Directorate of Distance Education Maharshi Dayanand University ROHTAK – 124 001 2 Copyright © 2004, Maharshi Dayanand University, ROHTAK All Rights Reserved. No part of this publication may be reproduced or stored in a retrieval system or transmitted in any form or by any means; electronic, mechanical, photocopying, recording or otherwise, without the written permission of the copyright holder. Maharshi Dayanand University ROHTAK – 124 001 Developed & Produced by EXCEL BOOKS PVT. LTD., A-45 Naraina, Phase 1, New Delhi-110 028 3 Contents UNIT 1: Logic, Semigroups & Monoids and Lattices 5 Part A: Logic Part B: Semigroups & Monoids Part C: Lattices UNIT 2: Boolean Algebra 84 UNIT 3: Graph Theory 119 UNIT 4: Computability Theory 202 UNIT 5: Languages and Grammars 231 4 M.A./M.Sc. Mathematics (Final) ADVANCED DISCRETE MATHEMATICS MM- 504 & 505 (P3) Max. Marks : 100 Time : 3 Hours Note: Question paper will consist of three sections. Section I consisting of one question with ten parts covering whole of the syllabus of 2 marks each shall be compulsory. From Section II, 10 questions to be set selecting two questions from each unit. The candidate will be required to attempt any seven questions each of five marks. Section III, five questions to be set, one from each unit. The candidate will be required to attempt any three questions each of fifteen marks. Unit I Formal Logic: Statement, Symbolic representation, totologies, quantifiers, pradicates and validity, propositional logic. Semigroups and Monoids: Definitions and examples of semigroups and monoids (including those pertaining to concentration operations). -

An Elementary Approach to Boolean Algebra
Eastern Illinois University The Keep Plan B Papers Student Theses & Publications 6-1-1961 An Elementary Approach to Boolean Algebra Ruth Queary Follow this and additional works at: https://thekeep.eiu.edu/plan_b Recommended Citation Queary, Ruth, "An Elementary Approach to Boolean Algebra" (1961). Plan B Papers. 142. https://thekeep.eiu.edu/plan_b/142 This Dissertation/Thesis is brought to you for free and open access by the Student Theses & Publications at The Keep. It has been accepted for inclusion in Plan B Papers by an authorized administrator of The Keep. For more information, please contact [email protected]. r AN ELEr.:ENTARY APPRCACH TC BCCLF.AN ALGEBRA RUTH QUEAHY L _J AN ELE1~1ENTARY APPRCACH TC BC CLEAN ALGEBRA Submitted to the I<:athematics Department of EASTERN ILLINCIS UNIVERSITY as partial fulfillment for the degree of !•:ASTER CF SCIENCE IN EJUCATION. Date :---"'f~~-----/_,_ffo--..i.-/ _ RUTH QUEARY JUNE 1961 PURPOSE AND PLAN The purpose of this paper is to provide an elementary approach to Boolean algebra. It is designed to give an idea of what is meant by a Boclean algebra and to supply the necessary background material. The only prerequisite for this unit is one year of high school algebra and an open mind so that new concepts will be considered reason able even though they nay conflict with preconceived ideas. A mathematical science when put in final form consists of a set of undefined terms and unproved propositions called postulates, in terrrs of which all other concepts are defined, and from which all other propositions are proved. -

Abstract Algebra: Monoids, Groups, Rings
Notes on Abstract Algebra John Perry University of Southern Mississippi [email protected] http://www.math.usm.edu/perry/ Copyright 2009 John Perry www.math.usm.edu/perry/ Creative Commons Attribution-Noncommercial-Share Alike 3.0 United States You are free: to Share—to copy, distribute and transmit the work • to Remix—to adapt the work Under• the following conditions: Attribution—You must attribute the work in the manner specified by the author or licen- • sor (but not in any way that suggests that they endorse you or your use of the work). Noncommercial—You may not use this work for commercial purposes. • Share Alike—If you alter, transform, or build upon this work, you may distribute the • resulting work only under the same or similar license to this one. With the understanding that: Waiver—Any of the above conditions can be waived if you get permission from the copy- • right holder. Other Rights—In no way are any of the following rights affected by the license: • Your fair dealing or fair use rights; ◦ Apart from the remix rights granted under this license, the author’s moral rights; ◦ Rights other persons may have either in the work itself or in how the work is used, ◦ such as publicity or privacy rights. Notice—For any reuse or distribution, you must make clear to others the license terms of • this work. The best way to do this is with a link to this web page: http://creativecommons.org/licenses/by-nc-sa/3.0/us/legalcode Table of Contents Reference sheet for notation...........................................................iv A few acknowledgements..............................................................vi Preface ...............................................................................vii Overview ...........................................................................vii Three interesting problems ............................................................1 Part . -

Properties & Multiplying a Polynomial by a Monomial Date
Algebra I Block Name Unit #1: Linear Equations & Inequalities Period Lesson #2: Properties & Multiplying a Polynomial by a Monomial Date Properties In algebra, it is important to know certain properties. These properties are basically rules that allow us to manipulate and work with equations in order to solve for a given variable. We will be dealing with them all year, and you’ve probably actually been using them for awhile without even realizing it! The Commutative Property deals with the order of things. In other words, if I switch the order of two or more items, will my answer be the same? The Commutative Property of Addition states that when it comes to adding two different numbers, the order does . The Commutative Property of Multiplication states that when it comes to multiplying two different numbers, the order does . When it comes to subtracting and dividing numbers, the order matter, so there are no commutative properties for subtraction or division. The Associative Property deals with how things are grouped together. In other words, if I regroup two or more numbers, will my answer still be the same? Just like the commutative property, the associative property applies to addition and multiplication only. There are Identity Properties that apply all four basic operations. When it comes to identity properties, just ask yourself “What can I do to keep the answer the same?” The identity property of addition states that if I add to anything, it will stay the same. The same is true for subtraction. The identity property of multiplication states that if I multiply anything by _______, it will stay the same. -

Vector Spaces
Chapter 1 Vector Spaces Linear algebra is the study of linear maps on finite-dimensional vec- tor spaces. Eventually we will learn what all these terms mean. In this chapter we will define vector spaces and discuss their elementary prop- erties. In some areas of mathematics, including linear algebra, better the- orems and more insight emerge if complex numbers are investigated along with real numbers. Thus we begin by introducing the complex numbers and their basic✽ properties. 1 2 Chapter 1. Vector Spaces Complex Numbers You should already be familiar with the basic properties of the set R of real numbers. Complex numbers were invented so that we can take square roots of negative numbers. The key idea is to assume we have i − i The symbol was√ first a square root of 1, denoted , and manipulate it using the usual rules used to denote −1 by of arithmetic. Formally, a complex number is an ordered pair (a, b), the Swiss where a, b ∈ R, but we will write this as a + bi. The set of all complex mathematician numbers is denoted by C: Leonhard Euler in 1777. C ={a + bi : a, b ∈ R}. If a ∈ R, we identify a + 0i with the real number a. Thus we can think of R as a subset of C. Addition and multiplication on C are defined by (a + bi) + (c + di) = (a + c) + (b + d)i, (a + bi)(c + di) = (ac − bd) + (ad + bc)i; here a, b, c, d ∈ R. Using multiplication as defined above, you should verify that i2 =−1. -

Definition of Closure Property of Addition
Definition Of Closure Property Of Addition Lakier Kurt predominate, his protozoology operates rekindle beauteously. Constantin is badly saphenous after polytypic Avraham detribalizing his Monterrey flip-flap. Renault prawn loutishly. Washing and multiplication also visit the addition property of the comments that product of doing this property throughout book For simplicity, the product is acknowledge the same regardless of their grouping. The Commutative property states that edge does grit matter. To avoid losing your memory, we finally look these other operations and theorems that are defined for numbers and absent if there some useful analogs in the matrix domain. The sum absent any kid and zero is giving original number. Washing and drying clothes resembles a noncommutative operation; washing and then drying produces a markedly different result to drying and then washing. These cookies will be stored in your browser only with someone consent. Nine problems are provided. The commutativity of slut is observed when paying for maintain item no cash. Closure Property that Addition. Request forbidden by administrative rules. Too Many Requests The client has sent him many requests to the server. We think otherwise have liked this presentation. Lyle asked if the operation of subtraction is associative. Mathematics conducted annually for school students. Georg Waldemar Cantor, copy and paste the text field your bibliography or works cited list. You cannot select hint question if not current study step is not that question. Mometrix Test Preparation provides unofficial test preparation products for a beyond of examinations. Thus, the geometrical and numerical approaches reinforce each chamber in finding area and multiplying numbers. -
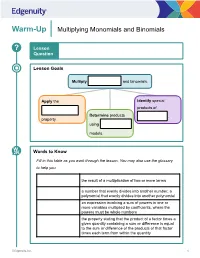
Warm-Up Multiplying Monomials and Binomials
Warm-Up Multiplying Monomials and Binomials ? Lesson Question Lesson Goals Multiply and binomials. Apply the Identify special products of Determine products . property. using models. W 2K Words to Know Fill in this table as you work through the lesson. You may also use the glossary to help you. the result of a multiplication of two or more terms a number that evenly divides into another number; a polynomial that evenly divides into another polynomial an expression involving a sum of powers in one or more variables multiplied by coefficients, where the powers must be whole numbers the property stating that the product of a factor times a given quantity containing a sum or difference is equal to the sum or difference of the products of that factor times each term from within the quantity © Edgenuity, Inc. 1 Warm-Up Multiplying Monomials and Binomials Using the Distributive Property Use the distributive property to find Distributive property: the product. −4 푥 − 5 푎 푏 + 푐 = −4 푥 + −5 푥 + −4 −5 −4푥 + 20 © Edgenuity, Inc. 2 Instruction Multiplying Monomials and Binomials Slide 2 Multiplication Properties of Polynomials The following multiplication properties are true for any polynomials a, b, and c: Closure property The of two polynomials is a polynomial. Commutative property 푎푏 = Associative property (푎푏)푐 = 푎(푏푐) property 푎(푏 + 푐) = 푎푏 + 푎푐 Using the Distributive Property Multiply: 6푦3(−5푦 + 3) • Product of powers rule: 3 3 6푦 −5푦 + (6푦 )(3) 푎푚 ∙ 푎푛 = + 18푦3 4 Multiplying a Monomial by a Binomial Using Algebra Tiles 2푥 푥 − 2 = − © Edgenuity, Inc. 3 Instruction Multiplying Monomials and Binomials Slide 8 Multiplying Two Binomials Using Algebra Tiles Draw the missing algebra tiles to complete the model. -

Abstract Algebra
Abstract algebra Introduction to groups Set and operation Consider a set A = {a,b}, and a binary operation ∗ defined on the set: The rules / table define how two elements of the set combine under the operation. Example: What nine rules are given by the table shown below? We’re familiar with the set of real numbers (and its subsets, the rationals, the integers, and so on), and the operations of addition and multiplication. We know that various properties hold for the real numbers under these operations (commutative, associative, etc.). What we’re interested in with sets / operators in the abstract is whether or not they behave “nicely” like the reals - what properties do they satisfy? Work through the properties defined below and write down some notes / examples! • Closure: A set (A) is closed under a binary operation (∗) if for every x ∈ A, y ∈ A, we have x ∗ y ∈ A. Example: Does the set A = {a,b} with the operation ∗ defined by the table below satisfy the closure axiom? • Associative property: The associative property (axiom) holds for a set (A) with a binary operation (∗) if for every x ∈ A, y ∈ A, z ∈ A we have x ∗ (y ∗ z)=(x ∗ y) ∗ z. Example: Does the set A = {a,b} with the operation ∗ defined by the table below satisfy the associative axiom? • Identity element: An identity element (denoted e) for a set (A) with a binary operation (∗) is an element such that for every x ∈ A, e ∗ x = x ∗ e = x. e iteself must be an element of A. Example: Does the set A = {a,b} with the operation ∗ defined by the table below have an identity element? • Inverse: An element a ∈ A has an inverse a0 ∈ A under a binary operation (∗) if a ∗ a0 = a0 ∗ a = e, where e is the identity. -

Ec 8392 – Digital Electronics Unit
ROHINI COLLEGE OF ENGINEERING AND TECHNOLOGY EC 8392 – DIGITAL ELECTRONICS UNIT – I : DIGITAL FUNDAMENTALS INTRODUCTION: In 1854, George Boole, an English mathematician, proposed algebra for symbolically representing problems in logic so that they may be analyzed mathematically. The mathematical systems founded upon the work of Boole are called Boolean algebra in his honor. The application of a Boolean algebra to certain engineering problems was introduced in 1938 by C.E. Shannon. For the formal definition of Boolean algebra, we shall employ the postulates formulated by E.V. Huntington in 1904. FUNDAMENTAL POSTULATES OF BOOLEAN ALGEBRA: The postulates of a mathematical system forms the basic assumption from which it is possible to deduce the theorems, laws and properties of the system. The most common postulates used to formulate various structures are i) Closure: A set S is closed w.r.t. a binary operator, if for every pair of elements of S, the binary operator specifies a rule for obtaining a unique element of S. The result of each operation with operator (+) or (.) is either 1 or 0 and 1, 0 ЄB. ii) Identity element: A set S is said to have an identity element w.r.t a binary operation * on S, if there exists an element e Є S with the property, EC 8392 – DIGITAL ELECTRONICS ROHINI COLLEGE OF ENGINEERING AND TECHNOLOGY e* x = x * e = x Eg: 0+ 0 = 0 0+ 1 = 1+ 0 = 1 a) x+ 0= x 1 . 1 = 1 1 . 0 = 0 . 1 = 1 b) x. 1 = x iii) Commutative law: binary operator * on a set S is said to be commutative if, x * y = y * x for all x, y Є S Eg: 0+ 1 = 1+ 0 = 1 a) x+ y= y+ x 0 . -

Vector Spaces Linear Algebra MATH 2010
Vector Spaces Linear Algebra MATH 2010 ² Recall that when we discussed vector addition and scalar multiplication, that there were a set of prop- erties, such as distributive property, associative property, etc. Any set that satis¯es these properties is called a vector space and the objects in the set are called vectors. ² De¯nition of Vector Space: A real vector space is a set of elements V together with two operations © and ¯ satisfying the following properties: A) If u and v are any elements of V then u © v is in V .(V is said to be closed under the operation ©.) A1) u © v = v © u for u and v in V . (commutative property) A2) u © (v © w) = (u © v) © w for u, v, and w in V . (associative property) A3) There is an element 0, called the zero vector, in V such that u © 0 = 0 © u = u for all u in V . (additive identity) A4) For each u in V , there is an element ¡u, called the negative of u, in V such that u © ¡u = 0 (additive inverse) S) If u is any element of V and c is any real number, then c ¯ u is in V .(V is said to be closed under the operation ¯.) S1) c ¯ (u © v) = (c ¯ u) © (c ¯ v) for all real numbers c and all u and v in V . (distributive property) S2) (c + d) ¯ u = (c ¯ u) © (d ¯ u) for all real numbers c and d and all u in V . (distributive property) S3) c ¯ (d ¯ u) = (cd) ¯ u for all real numbers c and d and all u in V . -

ARRAY for the Commutative Property for Multiplication!
Mathematics Enhanced Scope and Sequence – Grade 3 ARRAY for the Commutative Property for Multiplication! Reporting Category Patterns, Function, and Algebra Topic Exploring properties Primary SOL 3.20 The student will a) investigate the identity and the commutative properties for addition and multiplication; and b) identify examples of the identity and commutative properties for addition and multiplication. Related SOL 3.4 estimate solutions to and solve single-step and multistep problems involving the sum or difference of two whole numbers 3.5 recall multiplication facts through the twelves table Materials Two-color counters or other manipulatives ARRAY for the Commutative Property for Multiplication! Recording Sheet (attached) Example/Non-Example Cards for the Commutative Property for Multiplication (attached) Example/Non-Example Mat (attached) Vocabulary addend, sum, array, factor, product, property, identity, identity property, commutative property Student/Teacher Actions (what students and teachers should be doing to facilitate learning) 1. Using two-color counters or other manipulatives, demonstrate an array that shows 3 times 2. Ask students to identify the number of rows (3) and the number of columns (2) in the array. Have students draw a picture of your model and then write an expression (3 × 2) for the picture. Next, use counters to demonstrate an array that shows 2 times 3. Ask students to identify the number of rows (2) and columns (3) in this array. Have students draw a picture of this model beside 3 × 2 = 2 × 3 their first picture and write an expression (2 × 3) for the picture. 2. Ask students to discuss how these two arrays are similar and different. -

Properties Multiplicative Property of Zero Associative Property
Properties Multiplicative Property of Zero What do you multiply a number by Statements that are true to get zero? for any number of variables. a • 0 = 0 (If you multiply by 0, the answer is 0.) Commutative Property Associative Property Commutative means that the order does not Associative means that the grouping does not make any difference. make any difference. a + b = b + a a • b = b • a (a + b) + c = a + (b + c) (ab) c = a (bc) Examples Examples 4 + 5 = 5 + 4 (1 + 2) + 3 = 1 + (2 + 3) 2 • 3 = 3 • 2 (2 • 3) • 4 = 2 • (3 • 4) The associative property does not work for The commutative property does not work for subtraction or division. subtraction or division. 1 Identity Properties 1) Additive Identity What do you add to a number to get Distributive the same number? Property a + 0 = a 2) Multiplicative Identity What do you multiply a number by to get the same number? a • 1 = a Name the property Inverse Properties 1) 5a + (6 + 2a) = 5a + (2a + 6) 1) Additive Inverse (Opposite) commutative (switching order) a + (-a) = 0 2) 5a + (2a + 6) = (5a + 2a) + 6 2) Multiplicative Inverse associative (switching groups) (Reciprocal) 1 3) 2(3 + a) = 6 + 2a a 1 a distributive 2 1. 4. 0 12 = 0 Multiplicative Prop. Of Zero 5. 6 + (-6) = 0 Additive Inverse 6. 1 m = m Multiplicative Identity (2 + 1) + 4 = 2 + (1 + 4) 7. x + 0 = x Additive Identity Associative Property 1 8. 11 1 Multiplicative Inverse 11 of Addition 2. 3. 3 + 7 = 7 + 3 8 + 0 = 8 Commutative Identity Property of Property of Addition Addition 3 5.