DOCSLIB.ORG

1-Valence Bond Theory

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
1-Valence Bond Theory Structure Determination How can the structure of an unknown compound be determined? Before modern analytical tools were developed (for organic chemists this means the development of NMR (~1950s) or IR (first used ~1900, not readily obtained until mid 1900s), the only experimental evidence for the identity of an organic compound was elemental analysis A chemist could thus determine the % of various elements in an unknown sample For example, if a sample had 1 part carbon and 4 parts hydrogen (CH4) what is the constitution? H H H C H H H C H H How to test the possible structures? 1 Structure Determination In order to distinguish the possible constitutional isomers, experimentalists would react the compound in a substitution reaction and detect the number of isomeric products H H Cl H C H H C Cl H C H Obtain 1 isomer H H H Same compound H Cl H H H C H H C Cl H C Obtain isomers H H H Different compounds By reacting methane in a variety of reactions, it was determined that a monosubstitution always produced only 1 isomer, therefore all 4 hydrogens must be equivalent 2 Structure Determination In addition to the constitution, however, what was the configuration? How are the 4 equivalent hydrogens arranged in space? H H H C H H C H C H H H H H H Planar Pyramidal Tetrahedral H H H C Cl H C H C H H Cl Cl H H Each possible configuration would generate only 1 isomer with monosubstitution (thus the 4 hydrogens are at equivalent positions) React twice By logic, eventually a Cl H tetrahedral geometry Cl was proposed H C Cl Cl C Cl H C H Cl C H Cl Cl H Cl C H H H Cl H Two products Two products One product! 3 Structure Determination This was the state of affairs until the beginning of the 20th century, for any new compound the elemental analysis was obtained and then the structure was inferred by systematically running reactions or by comparing to analogous compounds Could a model be developed to predict the structure of organic compounds? In 1916 G.N. Lewis published a paper that hypothesized that bonding occurred by sharing electron pairs between atoms (in contrast to ionic bonds) We now call these structures “Lewis dot structures” by explicitly designating all valence electrons as a dot Only designate H B C N O F valence electrons The constitution could thus be predicted by filling the outer shell of electrons for each atom (second row atoms thus need 8 electrons and thus an octet rule) H O H Two electrons shared “resonance” Filled outer shell for all atoms 4 Structure Determination Original course notes from Lewis (1902) The cube indicated does not indicate easily how multiple bonds are formed, or what is the angle between various bonds C C C C ??? The Lewis dot structures work well to determine the constitution of a molecule (atoms are bonded in a way that allows a filled octet rule to form), but does not indicate configuration 5 Structure Determination The intuitive arguments of Lewis to determine constitution by sharing electrons to form a filled outer shell, however, were given mathematical basis by Heitler and London (1927) Studied binding energy of H2 molecule H H Figure from Heitler and If electron 1 was only London* associated with hydrogen 1 and electron 2 was only associated with hydrogen 2 H1 e1 H2 e2 If electron constraint was Calculated bond energy a removed and each electron fraction of actual can interact equally with both nuclei e1 H1 e H2 2 Energetic basis for a “bond” Calculated bond energy much -sharing of electrons between two atoms closer to actual *W. Heitler, F.Z. London, Z. Physik, 1927, (44), 455-472 6 Valence Bond Theory The intuitive description proposed by Lewis where bonds are formed between two atoms by sharing valence electrons in order to obtain a filled octet for the outer shell is basis of “Valence Bond Theory” This theory is still the underlying principle most organic chemists use to rationalize chemical reactions and predict chemical properties Two major results from valence bond theory: 1) Concept of Resonance Resonance structures result from electrons being associated with different nuclei For H-H molecule e1 e1 H1 e1 H2 e2 H1 e2 H2 e1 H1 H2 H1 H2 e2 e2 ΨMOL = c1 Ψ1 + c2 Ψ2 + c3 Ψ3 + c4 Ψ4 Actual structure is a combination of all contributing structures with appropriate weighting factors Called “principle of linear combination” 7 Resonance in Organic Compounds What is resonance? (also called ‘delocalization’) Look at a nitro group O RNO2 R N O The negative charge on the oxygen could be placed on either oxygen using Lewis structures O O R N R N O O Which structure is correct? It turns out neither structure is correct, but the charge is delocalized onto both oxygens -This process of being able to delocalize the charge onto more than one atom is called resonance (Resonance is a result of not being able to draw an accurate structure using one Lewis structure) 8 Resonance in Organic Compounds “Rules” of Resonance 1. All resonance structures must be valid Lewis structures (e.g. cannot have 10 electrons on one carbon in one structure) 2. Only electrons move (cannot move nuclei, only electrons – usually double bonds or lone pairs connected through an extended p orbital system) 3. Number of unpaired electrons must be constant 9 Resonance in Organic Compounds Concept of resonance allows explanation of a number of chemical properties How does resonance explain acidity? Consider pKa of organic molecules pKa CH3CH2OH CH3CH2O H 16 O O H3C H3C H 4.8 OH O Resonates similar to nitro group Both structures place a negative charge on oxygen after loss of proton, but the pKa difference is greater than 11 10 Resonance in Organic Compounds A carbonyl group is a common resonance source O -H O O H3C H3C H3C O H O O Once the acid is deprotonated, the negative charge is located on one oxygen The charge can be delocalized (resonated) onto the other oxygen Neither structure is correct, but rather the negative charge can be delocalized over both oxygen atoms Resonance structures are simply a result of one Lewis structure being incomplete in describing the location of electrons A double headed arrow always means two (or more) resonance forms Two arrows mean two chemically distinct structures 11 Resonance in Organic Compounds Comparison of Electron Density for Ethoxide versus Acetate anion O O O CH3CH2OH CH3CH2O H3C H3C H3C OH O O The excess negative charge is more stable on the acetate anion that can resonate, thus the conjugate acid is more acidic 12 Resonance in Organic Compounds Resonance also allows explanation for the concept of electronegativity Electrons in a chemical bond need not be shared equally between two nuclei For H-Cl molecule e1 e1 H e1 Cl e2 H e2 Cl e1 H Cl H Cl e2 e2 ΨMOL = c1 Ψ1 + c2 Ψ2 + c3 Ψ3 + c4 Ψ4 Unlike with H2 where the Ψ1 and Ψ2 wavefunctions were more stable than the charged wave functions, with HCl the Ψ4 wave function is the most stable, therefore highest coefficient The electrons are more stable closer to Cl than H, therefore the chlorine atom is said to be more “electronegative” than the hydrogen atom These resonance considerations therefore also cause bond dipoles in unsymmetrical bonds 13 Electronegativity Tables Linus Pauling first established values to associate with each element (there have been many different values computed, but the trend is the same) Elements toward the upper right hand of the periodic table are more electronegative Also can predict the relative electronegativity of two atoms by their relative placement in the periodic table H (2.3) Li (0.9) Be (1.6) B (2.1) C (2.5) N (3.1) O (3.6) F (4.2) Cl (2.9) H3C OH Br (2.7) 2.5 3.6 I (2.4) The numbers are a relative indication of how much the electrons are ‘attracted’ to a certain atom As the number becomes larger, the electrons are attracted more by that atom 14 Resonance in Organic Compounds The bond dipoles resulting from unsymmetrical bonds also can affect the acidity O O pKa H 4.8 H3C OH H3C O O O H 0.7 Cl3C OH Cl3C O Anion with trichloroacetic acetate is stabilized by inductive effects from polarized C-Cl bonds O Cl C O Cl Cl 15 Induction Induction refers to electron movement “through bonds” -All bonds between different atoms are polar and the electrons are closer to the more electronegative atom “on time average” As the electronegative atom is further removed, the inductive effect is less (inductive stabilization is through bonds, therefore if there are more bonds to transverse the effect is less) O O F Base F OH O H H H H X pKa The electronegative H 4.8 fluorine pulls electron I 3.2 density away from F 2.6 carboxylate 16 Field Effect Can have similar effect merely through space (field) rather than through bonds (inductive) H Cl Cl H H Cl Cl H CO2H CO2H Which is more acidic? H Cl Cl H H Cl Cl H CO2 CO2 17 Resonance in Organic Compounds Important to Remember: Not all resonance structures need to contribute equally If two resonance structures are not of equal energy, then they will not contribute equally to the actual structure H H H H N N H H H H Octet rule obeyed Positive charge on on all atoms less electronegative atom This leads to major and minor contributors 18 Resonance Forms H H H H N N H H H H Deeper blue color on carbon (less charge on carbon) Actual “hybrid” structure 19 Resonance Forms O O O O H C CH H3C CH3 H3C CH3 H3C CH3 3 3 major minor inconsequential Only a resonance form if spins are paired Not all resonance forms need to contribute equally, but rather a weighting factor is given to each resonance form depending upon its importance to the actual form Typically forms with more bonds are more important (often due to forms
Load more

Recommended publications
  • Organometallic Chemistry from the Interacting Quantum Atoms Approach
    CORSO DI DOTTORATO DI RICERCA IN SCIENZE CHIMICHE CICLO XXIII TESI DI DOTTORATO DI RICERCA ORGANOMETALLIC CHEMISTRY FROM THE INTERACTING QUANTUM ATOMS APPROACH sigla del settore scientifico disciplinare CHIM03 NOME DEL TUTOR NOME DEL DOTTORANDO Prof: Angelo Sironi Davide Tiana NOME DEL COORDINATORE DEL DOTTORATO Prof. Silvia Ardizzone ANNO ACCADEMICO 2009/2010 1 2 Index Introduction ............................................................................................................................................................................ 5 The ligand field theory (LFT) .................................................................................................................................... 5 The chemistry from a real space point of view ................................................................................................. 9 Chapter 1: The quantum theory of atoms in molecules (QTAM) ............................................................... 12 Topological analysis of electron charge density ........................................................................................... 12 Analysis of the electronic charge density Laplacian ................................................................................... 16 Other properties ........................................................................................................................................................... 18 Chapter 2: The interacting quantum atoms theory (IQA) ............................................................................
    [Show full text]
  • Resonance, and Formal Charge
    3.091: Introduction to Solid State Chemistry Maddie Sutula, Fall 2018 Recitation 8 1 Resonance Often, there are many ways that electrons can be arranged around a molecule. The existence of multiple electronic configurations that are stable leads to resonance, which describes the delocalization of electrons in covalently bonded molecules. To be considered resonance structures, molecules must meet the following criteria: 1. Atoms must be in the same orientation relative to each other 2. All resonance structures must have the same number of valence electrons 3. The octet rule must be satisfied, with a few exceptions: - Not followed by some elements in periods three and higher, including Cl, Br, I, P, Si − - Sulfur can have up to 12 e − - Boron can have 6 e 4. Formal charge should be on the most electronegative atoms 2− Example: Draw resonance structures for ozone (O3) and CO3 . Ozone consists of three oxygen atoms, for a total of 18 valence electrons. These can be equivalently dis- tributed in two ways: 2− CO3 consists of a central carbon atom which brings 4 valence electrons, and four oxygen atoms that each bring 6 electrons, and two additional electrons that yield the additional 2− charge. The resonance structures can be represented as follows: These equivalent structures can be combined into one compact picture (shown above on the right) that is an average of the possible structures. All of the resonance structures are equally likely, as they equivalently satisfy the guidelines for stable Lewis structures. 1 3.091: Introduction to Solid State Chemistry Maddie Sutula, Fall 2018 Recitation 8 2 Formal charge (again) 2− In the CO3 example above, the formal charge on each atom is shown in circles.
    [Show full text]
  • Constrained Density Functional Theory
    Constrained Density Functional Theory The MIT Faculty has made this article openly available. Please share how this access benefits you. Your story matters. Citation Kaduk, Benjamin, Tim Kowalczyk, and Troy Van Voorhis. “Constrained Density Functional Theory.” Chemical Reviews 112.1 (2012): 321–370. © 2012 American Chemical Society As Published http://dx.doi.org/ 10.1021/cr200148b Publisher American Chemical Society (ACS) Version Author's final manuscript Citable link http://hdl.handle.net/1721.1/74564 Terms of Use Article is made available in accordance with the publisher's policy and may be subject to US copyright law. Please refer to the publisher's site for terms of use. Constrained Density Functional Theory Benjamin Kaduk, Tim Kowalczyk and Troy Van Voorhis Department of Chemistry, Massachusetts Institute of Technology 77 Massachusetts Avenue, Cambridge MA 02139 May 2, 2011 Contents 1 Introduction 3 2 Theory 7 2.1 OriginalCDFTEquations ............................ 7 2.2 ConstrainedObservables . .. .. 9 2.3 ChoosingaConstraint .............................. 13 2.4 Implementation .................................. 18 2.5 Promolecules ................................... 24 2.6 Illustrations .................................... 28 2.6.1 MetalImpurities ............................. 28 2.6.2 Long-range Charge-Transfer Excited States . .... 32 2.7 FutureChallenges................................. 34 3 Application to Electron Transfer 36 3.1 Background:MarcusTheory. 36 3.2 DiabaticETStatesfromCDFT ......................... 39 3.2.1 Choosing Suitable Density Constraints for ET . 39 3.2.2 Illustrations ................................ 41 3.3 IncorporatingSolventEffects. .. 46 3.4 Molecular Dynamics and Free Energy Simulations . 49 3.5 RelatedandOngoingWork ........................... 54 4 Low-lying Spin States 57 4.1 TracingOutConstant-spinStates . .. 59 4.2 The Heisenberg Picture of Molecular Magnets . .. 63 4.3 Singlet-Triplet Gaps of Intermolecular CT States .
    [Show full text]
  • Formal Charge Worksheet / Chem 314 Beauchamp
    Formal Charge Worksheet / Chem 314 Beauchamp Formal Charge – a convention designed to indicate an excess or deficiency of electron density compared to an atom’s neutral allocation of electrons. Formal electrons in 1 electrons in Charge =Zeffective lone pairs 2 covalent bonds This number never changes for an atom and represents positive Total valence electrons allocated to an atom charge not cancelled assuming electrons are shared evenly in bonds. by core electrons. This number varies depending on the bonding arrangement. It is negative because electrons are negative. Rules of Formal Charge 1. When an atom’s total valence electron credit exactly matches its Zeff, there is no formal charge. 2. Each deficiency of an electron credit from an atom’s normal number of valence electrons produces an additional positive charge. 3. If the formal charge calculation shows excess electron credit over an atom’s normal number of valence electrons, a negative formal charge is added for each extra electron. 4. The total charge on an entire molecule, ion or free radical is the sum of all of the formal charges on the individual atoms. Write 3D structures for all resonance contributors. Rank them from best (=1) to last. Judge your structures on the basis of 1. maximum number of bonds / full octets, 2. minimize formal charge, 3, consistent formal charge based on electronegativity. Cations a. b. c. d. e. f. H COH 2 H2CNH2 (CH3)2COH (CH3)2CNHCH3 (CH3)2CCH2CH3 H2CCOH 2 resonance 2 resonance 2 resonance 2 resonance 2 resonance structures structures structures structures structures g. h. i. j.
    [Show full text]
  • Polar Covalent Bonds: Electronegativity
    Polar Covalent Bonds: Electronegativity Covalent bonds can have ionic character These are polar covalent bonds Bonding electrons attracted more strongly by one atom than by the other Electron distribution between atoms is not symmetrical Bond Polarity and Electronegativity Symmetrical Covalent Bonds Polar Covalent Bonds C – C + - C – H C – O (non-polar) (polar) Electronegativity (EN): intrinsic ability of an atom to attract the shared electrons in a covalent bond Inductive Effect: shifting of sigma bonded electrons in resppygonse to nearby electronegative atom The Periodic Table and Electronegativity C – H C - Br and C - I (non-pol)lar) (po l)lar) Bond Polarity and Inductive Effect Nonpolar Covalent Bonds: atoms with similar EN Polar Covalent Bonds: Difference in EN of atoms < 2 Ionic Bonds: Difference in EN > 2 C–H bonds, relatively nonpolar C-O, C-X bonds (more electronegative elements) are polar Bonding electrons shift toward electronegative atom C acqqppuires partial positive char g,ge, + Electronegative atom acquires partial negative charge, - Inductive effect: shifting of electrons in a bond in response to EN of nearby atoms Electrostatic Potential Maps Electrostatic potential maps show calculated charge distributions Colors indicate electron- rich (red) and electron- poor (blue ) reg ions Arrows indicate direction of bond polarity Polar Covalent Bonds: Net Dipole Moments Molecules as a whole are often polar from vector summation of individual bond polarities and lone-pair contributions Strongly polar substances soluble in polar solvents like water; nonpolar substances are insoluble in water. Dipole moment ( ) - Net molecular polarity, due to difference in summed charges - magnitude of charge Q at end of molecular dipole times distance r between charges = Q r, in debyes (D), 1 D = 3.336 1030 coulomb meter length of an average covalent bond, the dipole moment would be 1.60 1029 Cm, or 4.80 D.
    [Show full text]
  • Heterocycles 2 Daniel Palleros
    Heterocycles 2 Daniel Palleros Heterocycles 1. Structures 2. Aromaticity and Basicity 2.1 Pyrrole 2.2 Imidazole 2.3 Pyridine 2.4 Pyrimidine 2.5 Purine 3. Π-excessive and Π-deficient Heterocycles 4. Electrophilic Aromatic Substitution 5. Oxidation-Reduction 6. DNA and RNA Bases 7. Tautomers 8. H-bond Formation 9. Absorption of UV Radiation 10. Reactions and Mutations Heterocycles 3 Daniel Palleros Heterocycles Heterocycles are cyclic compounds in which one or more atoms of the ring are heteroatoms: O, N, S, P, etc. They are present in many biologically important molecules such as amino acids, nucleic acids and hormones. They are also indispensable components of pharmaceuticals and therapeutic drugs. Caffeine, sildenafil (the active ingredient in Viagra), acyclovir (an antiviral agent), clopidogrel (an antiplatelet agent) and nicotine, they all have heterocyclic systems. O CH3 N HN O O N O CH 3 N H3C N N HN N OH O S O H N N N 2 N O N N O CH3 N CH3 caffeine sildenafil acyclovir Cl S N CH3 N N H COOCH3 nicotine (S)-clopidogrel Here we will discuss the chemistry of this important group of compounds beginning with the simplest rings and continuing to more complex systems such as those present in nucleic acids. Heterocycles 4 Daniel Palleros 1. Structures Some of the most important heterocycles are shown below. Note that they have five or six-membered rings such as pyrrole and pyridine or polycyclic ring systems such as quinoline and purine. Imidazole, pyrimidine and purine play a very important role in the chemistry of nucleic acids and are highlighted.
    [Show full text]
  • Chemical Bonding II: Molecular Shapes, Valence Bond Theory, and Molecular Orbital Theory Review Questions
    Chemical Bonding II: Molecular Shapes, Valence Bond Theory, and Molecular Orbital Theory Review Questions 10.1 J The properties of molecules are directly related to their shape. The sensation of taste, immune response, the sense of smell, and many types of drug action all depend on shape-specific interactions between molecules and proteins. According to VSEPR theory, the repulsion between electron groups on interior atoms of a molecule determines the geometry of the molecule. The five basic electron geometries are (1) Linear, which has two electron groups. (2) Trigonal planar, which has three electron groups. (3) Tetrahedral, which has four electron groups. (4) Trigonal bipyramid, which has five electron groups. (5) Octahedral, which has six electron groups. An electron group is defined as a lone pair of electrons, a single bond, a multiple bond, or even a single electron. H—C—H 109.5= ijj^^jl (a) Linear geometry \ \ (b) Trigonal planar geometry I Tetrahedral geometry I Equatorial chlorine Axial chlorine "P—Cl: \ Trigonal bipyramidal geometry 1 I Octahedral geometry I 369 370 Chapter 10 Chemical Bonding II The electron geometry is the geometrical arrangement of the electron groups around the central atom. The molecular geometry is the geometrical arrangement of the atoms around the central atom. The electron geometry and the molecular geometry are the same when every electron group bonds two atoms together. The presence of unbonded lone-pair electrons gives a different molecular geometry and electron geometry. (a) Four electron groups give tetrahedral electron geometry, while three bonding groups and one lone pair give a trigonal pyramidal molecular geometry.
    [Show full text]
  • Formal Charge and Oxidation Number
    FORMAL CHARGE AND OXIDATION NUMBER Although the total number of valence electrons in a molecule is easily calculated, there is not aways a simple and unambiguous way of determining how many reside in a particular bond or as non-bonding pairs on a particular atom. For example, one can write valid Lewis octet structures for carbon monoxide showing either a double or triple bond between the two atoms, depending on how many nonbonding pairs are placed on each: C::O::: and :C:::O: (see Problem Example 3 below). The choice between structures such as these is usually easy to make on the principle that the more electronegative atom tends to surround itself with the greater number of electrons. In cases where the distinction between competing structures is not all that clear, an arbitrarily-calculated quantity known as the formal charge can often serve as a guide. The formal charge on an atom is the electric charge it would have if all bonding electrons were shared equally with its bonded neighbors. How to calculate the formal charge on an atom in a molecule The formal charge on an atom is calculated by the following formula: In which the core charge is the electric charge the atom would have if all its valence electrons were removed. In simple cases, the formal charge can be worked out visually directly from the Lewis structure, as is illustrated farther on. Problem Example 1 Find the formal charges of all the atoms in the sulfuric acid structure shown here. Solution: The atoms here are hydrogen, sulfur, and double- and single-bonded oxygens.
    [Show full text]
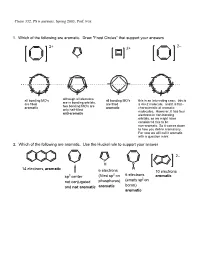
  • PS 6 Answers, Spring 2003, Prof
    Chem 332, PS 6 answers, Spring 2003, Prof. Fox 1. Which of the following are aromatic. Draw "Frost Circles" that support your answers 2– 2+ 2+ + all bonding MO's although all electrons all bonding MO's this is an interesting case: this is are in bonding orbitals, are filled are filled a 4n+2 molecule, and it is flat-- two bonding MO's are aromatic aromatic characteristic of aromatic only half-filled molecules. However, it has four anti-aromatic electrons in non-bonding orbitals, so we might have considered this to be non-aromatic. So it comes down to how you define aromaticity. For now we will call it aromatic with a question mark. 2. Which of the following are aromatic. Use the Huckel rule to support your answer 2– P H B 14 electrons, aromatic H 6 electrons 10 electrons 2 6 electrons sp3 center (filled sp on aromatic (empty sp2 on not conjugated phosphorus) boron) and not aromatic aromatic aromatic 3. Compound 1 has an unusually large dipole moment for an organic hydrocarbon. Explain why (consider resonance structures for the central double bond) We need to remember that for any double bond compound, we can draw two polar resonance structure. Normally, these resonance structures are unimportant unimportant unimportant However, for 1 the story is different because there is a polar resonance form that has two aromatic components. In other words, 'breaking' the double bond gives rise to aromaticity, and therefore the polar resonance structure is important and leads to the observed dipole. dipole 1 8 e– 4 e– 6 e– 6 e– anti- anti- aromatic aromatic aromatic aromatic important resonance unimportant resonance structure structure 5.
    [Show full text]
  • Structure of Benzene, Orbital Picture, Resonance in Benzene, Aromatic Characters, Huckel’S Rule B
    Dr.Mrityunjay Banerjee, IPT, Salipur B PHARM 3rd SEMESTER BP301T PHARMACEUTICAL ORGANIC CHEMISTRY –II UNIT I UNIT I Benzene and its derivatives 10 Hours A. Analytical, synthetic and other evidences in the derivation of structure of benzene, Orbital picture, resonance in benzene, aromatic characters, Huckel’s rule B. Reactions of benzene - nitration, sulphonation, halogenationreactivity, Friedelcrafts alkylation- reactivity, limitations, Friedelcrafts acylation. C. Substituents, effect of substituents on reactivity and orientation of mono substituted benzene compounds towards electrophilic substitution reaction D. Structure and uses of DDT, Saccharin, BHC and Chloramine Benzene and its Derivatives Chemists have found it useful to divide all organic compounds into two broad classes: aliphatic compounds and aromatic compounds. The original meanings of the words "aliphatic" (fatty) and "aromatic" (fragrant/ pleasant smell). Aromatic compounds are benzene and compounds that resemble benzene in chemical behavior. Aromatic properties are those properties of benzene that distinguish it from aliphatic hydrocarbons. Benzene: A liquid that smells like gasoline Boils at 80°C & Freezes at 5.5°C It was formerly used to decaffeinate coffee and component of many consumer products, such as paint strippers, rubber cements, and home dry-cleaning spot removers. A precursor in the production of plastics (such as Styrofoam and nylon), drugs, detergents, synthetic rubber, pesticides, and dyes. It is used as a solvent in cleaning and maintaining printing equipment and for adhesives such as those used to attach soles to shoes. Benzene is a natural constituent of petroleum products, but because it is a known carcinogen, its use as an additive in gasoline is now limited. In 1970s it was associated with leukemia deaths.
    [Show full text]
  • Resonance 1. Lone Pair Next to Empty 2P Orbital
    1 Lecture 5 Resonance 1. Lone pair next to empty 2p orbital electron pair acceptors - lack of electrons C C CC sp2 R+ is more common sp R+ is less common R+ needs electrons, has to overlap with a. an adjacent 2p lone pair with electrons b. an adjacent pi bond a. an adjacent 2p lone pair with electrons on a neutral atom (+ overall, delocalization of positive charge) R R X = neutral atom with lone pair R R C C R X 2D resonance R X C C R X R X R R R R C R C R CX CX R N R N R 3D resonance R R R R R R R C R C R CX R O CX 3D resonance R O R R R R C better, more bonds, full octets C R F R F b. an adjacent 2p lone pair with electrons on a negative atom (neutral overall, delocalization of electrons) R R X =anion with lone pair R R C C R X 2D resonance R X C C R X R X R R R R C R C R CX CX R C R C R 3D resonance R R R R R R R C R C R CX R N CX 3D resonance R N R R R R C C better, more bonds, full octets R O R O 2 Lecture 5 Problem 1 – All of the following examples demonstrate delocalization of a lone pair of electrons into an empty 2p orbital. Usually in organic chemistry this is a carbocation site, but not always.
    [Show full text]
  • Chemical Bonding
    Chemical Bonding: Fundamental Concepts Resonance Structures and Formal Charge Electronegativity, Formal Charge and Resonance Page [1 of 3] In this lecture we’re going to pull together ideas about formal charge, resonance structures, electronegativity, and really make some predictions and some rationalizations about why molecules behave the way they do. And the first one I want to do is to go back and look at the cyanate ion. Cyanate is NCO. And in a previous lecture I talked about the fact that there were several different possible resonance structures that are all in equivalence, and that it was possible at least to figure out which one contributed the most and which one contributed the least based on formal charge. So here are the formal charge evaluations for this left-hand resonance structure. Nitrogen has a formal charge of zero. Carbon has a formal charge of zero. Oxygen has a formal charge of -1. For B, nitrogen is -1, carbon is zero, oxygen is zero. And for C, nitrogen is -2, carbon is zero, and oxygen is +1. Now, the rule said that formal charges of plus or minus 1 and zero are okay. In fact, zero is great. And plus or minus 2 and bigger, that’s just not going to work. Why? Because remember, formal charges reflect how the electrons are distributed relative to how they are distributed in the free atom. So how they’re distributed in a molecule versus how they’re distributed in the free atom. And in this case nitrogen has a lot more electrons than it would if were a free atom formally; in other words, an accounting method.
    [Show full text]