DOCSLIB.ORG

Roots of Unity Given a Positive Integer N, a Complex Number Z Is Called An

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Roots of Unity Given a Positive Integer N, a Complex Number Z Is Called An Chapter 3: Roots of Unity Given a positive integer n, a complex number z is called an nth root of unity if zn = 1. In other words, z is a root of the polynomial Xn 1. Denote by ω , or simply − n by ω if n is understood, the complex number e2πi/n: 2π 2π ω ω = e2πi/n cos + i sin . ≡ n ≡ n n From ωn = (e2πi/n)n = e(2πi/n)n = e2πi = 1 we see that ω is an nth root of unity. The complex numbers 1, ω, ω2, . , ωn−1, (3.1) considered as points in the complex plane, are vertices of a regular n-gon inscribed in the unit circle. For example, when n = 6, they are vertices of a hexagon, as shown in the following figure: Because of this particular geometric arrangement of 1, ω, ω2, . , ωn−1, it is not hard to believe that their sum is zero: 1 + ω + ω2 + ... + ωn−1 = 0. (3.2) We give an algebraic proof of this extremely important identity. From ωn = 1, we have (1 ω)(1 + ω + ω2 + ... + ωn−1) = 1 ωn = 0. − − Clearly ω = 1, that is 1 ω = 0. Hence (2) follows. − Each of ω, ω2, . , ωn−1 is an nth root of unity. Indeed, take z = ωk with 0 k n 1. Then ≤ ≤ − zn = (ωk)n = ωkn = (ωn)k = 1k = 1. 1 Thus 1, ω, ω2, . , ωn−1 are exactly n distinct roots of Xn 1. Each root ωk contributes − to a linear factor X ωk of Xn 1. Hence we have the following factorization of Xn 1: − − − n−1 Xn 1 = (X 1)(X ω)(X ω2) (X ωn−1) = (X ωk). (3.3) − − − − ··· − − k= 0 The last expression is read as the product of X ωk, where k runs from 0 to n 1. − − Exercise 3.1. Prove that n−1 1 ωk = 1. Give a geometric interpretation of this k= 1 | − | identity. Hint: Deduce from (3.3) that n−1(X ωk) = 1 + X + X2 + + Xn−1. k= 1 − ··· Notice that, since ω = 1, we have ωω = ω 2 = 1 and hence ω−1 = ω. On the | | | | other hand, ωn = 1 gives ωn−1ω = 1 and hence ωn−1 = ω−1. Thus we have ωn−1 = ω. Furthermore, from ωn−2ω2 = 1 we have ωn−2 = ω−2 = (ω−1)2 = ω2. we can continue in this manner to get ωn−3 = ω3, etc. In general, we have ωn−k = ωk (3.4) for k = 0, 1, . , n 1. − Example 3.1. Consider the case n = 5. In this case we have 2π 2π ω = e2πi/5 cos + i sin . ≡ 5 5 We are asked to find the value of cos 2π/5. Notice that cos 2π/5 is the real part of ω, that is, (ω + ω)/2. So it is enough to find ω + ω. In the present case, (2) gives 1 + ω + ω2 + ω3 + ω4 = 0. On the other hand, (3.4) above gives ω4 = ω and ω3 = ω2. Thus we have 1 + ω + ω2 + ω2 + ω = 0, or 1 + (ω + ω) + (ω2 + ω2) = 0. Now (ω + ω)2 = ω2 + ω2 + 2ωω = ω2 + ω2 + 2. (Recall that ωω = ω 2 = 1.). So | | ω2 + ω2 = (ω + ω)2 2. − 2 Hence 1 + (ω + ω) + (ω2 + ω2) = 0 becomes (ω + ω)2 + (ω + ω) 1 = 0. We have shown − that ω+ω 2 cos 2π/5 is a root of X2 +X 1. The roots of X2 +X 1 can be obtained ≡ − − by the usual formula for solving quadratic equations. The result is X = ( 1 √5)/2. − ± Since cos 2π/5 is a positive number, necessarily 2 cos 2π/5 = ( 1 + √5)/2. Thus − 2π √5 1 cos = − 5 4 which is the answer we are looking for. Example 3.2. Now we try to factorize the polynomial X5 1 into a product of real − polynomials. In the present case, identity (3.3) becomes X5 1 = (X 1)(X ω)(X ω2)(X ω3)(X ω4). (3.5) − − − − − − This is not the factorization we are seeking for, since X ωk (1 k 4) are not real − ≤ ≤ polynomials. Using ω4 = ω and ω3 = ω2, we rewrite this identity as X5 1 = (X 1) (X ω)(X ω) (X ω2)(X ω2) . − − { − − }{ − − } Now (X ω)(X ω) = X2 (ω + ω)X + ωω. From the previous example we see that − − − ω + ω = (√5 1)/2 and ωω = 1. So we have − √5 1 (X ω)(X ω) = X2 − X + 1 − − − 2 which is a real polynomial. Next, we have (X ω2)(X ω2) = X2 (ω2 + ω2)X + ω2ω2. − − − Here, ω2ω2 = (ωω)2 = 1 and 2 √5 1 √5 + 1 ω2 + ω2 = (ω + ω)2 2 = − 2 = . − 2 − − 2 Substituting the last expressions into (5), we have 1 √5 1 + √5 x5 1 = (x 1) x2 + − x + 1 x2 + x + 1 , − − 2 2 which is the required factorization. Example 3.3. We would like to find the values of cos π/12 and sin π/12. As we know, it is wise to consider eiπ/12 instead. The following computation is inspired by a 1 1 1 simple observation: = . 12 3 − 4 π π π π eπi/12 = e(πi/3)−(πi/4) = eπi/3e−πi/4 = cos + i sin cos i sin 3 3 4 − 4 1 √3 √2 √2 √6 + √2 √6 √2 = + i i = + i − . 2 2 2 − 4 2 4 3 π √6 + √2 π √6 √2 Hence we have cos = and sin = − . 12 4 12 4 Alternatively, we let ω = a + bi = eπi/12. Then √3 1 ω2 = eπi/6 = + i. 2 2 On the other hand, ω2 = (a2 b2) + 2ab i. Comparing the real and the imaginary parts of − these two expressions of ω, we obtain 1 √3 2ab = and a2 b2 = . 2 − 2 Add the last identity to a2 + b2 = ω 2 = 1, we get | | 1 + √3 2a2 = . 2 Dividing both sides by 2 and then taking the square root, we arrive at π 1 cos = a = 1 + √3. 12 2 The reader should check that this is the same answer as the previous one for cos π/12, even though they look different. √6 + √2 1 Exercise 3.2. Verify = 1 + √3 directly. 4 2 Exercise 3.3. Plot the points of the set Z[ω] Z + Zω ≡ consisting of all those complex numbers of the form a+bω, where a, b are integers, for each of the following values of ω: (a) ω = i; (b) ω = eπi/6; (c) ω = eπi/3. Exercise 3.4. Let ω = e2πi/3 and consider the ring R = Z[ω] Z+Zω; for the notation, ≡ see the last exercise). Prove: (a) for each Z R, z 2 is an integer; and (b)* if an element ∈ | | z in R is invertible (in the sense that there is an element w in R such that zw = 1), then z is one of the following: 1, i, (1 + ω). (The “*” sign means that it is optional.) ± ± ± Take any positive integer and let ω = e2πi/n. Consider the set C = 1, ω, ω2, ω3, . , ωn−1 n { } 4 of all nth roots of unity. This set forms a group with respect to multiplication in the sense that any product of two elements in Cn is also in Cn and any element in Cn has an inverse 7 4 6 10 7+ 3 3 in Cn. For example, when n = 7, we have ω = 1 and hence ω ω = ω = ω = ω , ω−3 = ω7ω−3 = ω4, etc. The group Cn is a cyclic group in the sense that there is an element called a gen- erator, such that its powers fill the whole group. Clearly, ω is a generator. But usually this is not the only one. More Exercises 3.5. Write out all nth roots of unity, for the following values of n: n = 2, 3, 4, 6, 8, 12. 3.6. Let ω = eπi/3. Check: (a) 1+ω3 = 0, 1+ω2 +ω4 = 0 and 1+ω+ω2 +ω3 +ω4 +ω5 = 0; (b) ω + ω5 = 1, ω ω5 = √3 i and ω4 = ω2. − 3.7. Check that if ω = eπi/m (m is a positive integer), then, for any integer k, ωk = ωm+ k. − 3.8. Verify that if ω = e2πi/5, then a = ω + ω4 and b = ω2 + ω3 are roots of t2 + t 1. − 3.9. Prove that if n 3 and if ω = 2πi/n, then 1 + ω2 + ω4 + ω6 + + ω2n−2 = 0. ≥ ··· 3.10 Factorize the polynomials X6 1 and X8 1 into real (irreducible) polynomials as in − − Example 3.2. 3.11 Verify that if ω = e2πi/7, then a = ω + ω2 + ω4 and b = ω3 + ω5 + ω6 are roots of t2 + t + 2. The material of the rest of this chapter is optional. We continue with the discussion of the cyclic group Cn. Suppose that m is a positive integer divisible by n, say n = mk, where k is another positive integer. Then Cm is generated by e2πi/m. By the substitution m = n/k, e2πi/m becomes e2πik/n ωk; (here, ≡ we still use the symbol ω for e2πi/n). Clearly a power of ωk is a power of ω. This shows that Cm is contained in Cn. Certainly Cm is itself a group under multiplication. So l Cm is a subgroup of Cn. To give a simple example to illustrate this, let us take n = 6 so that ω = e2πi/6 ωpii/3. Then ω6 = 1 and C = 1, ω, ω2, ω3, ω4, ω5 . Both C and C ≡ 6 { } 2 3 are subgroups of C ; in fact, C = 1, ω3 1, 1 and C = 1, ω2, ω4 1, η, η2 , 6 2 { } ≡ { − } 3 { } ≡ { } where η = ω2 e2πi/3.
Load more

Recommended publications
  • Algorithmic Factorization of Polynomials Over Number Fields
    Rose-Hulman Institute of Technology Rose-Hulman Scholar Mathematical Sciences Technical Reports (MSTR) Mathematics 5-18-2017 Algorithmic Factorization of Polynomials over Number Fields Christian Schulz Rose-Hulman Institute of Technology Follow this and additional works at: https://scholar.rose-hulman.edu/math_mstr Part of the Number Theory Commons, and the Theory and Algorithms Commons Recommended Citation Schulz, Christian, "Algorithmic Factorization of Polynomials over Number Fields" (2017). Mathematical Sciences Technical Reports (MSTR). 163. https://scholar.rose-hulman.edu/math_mstr/163 This Dissertation is brought to you for free and open access by the Mathematics at Rose-Hulman Scholar. It has been accepted for inclusion in Mathematical Sciences Technical Reports (MSTR) by an authorized administrator of Rose-Hulman Scholar. For more information, please contact [email protected]. Algorithmic Factorization of Polynomials over Number Fields Christian Schulz May 18, 2017 Abstract The problem of exact polynomial factorization, in other words expressing a poly- nomial as a product of irreducible polynomials over some field, has applications in algebraic number theory. Although some algorithms for factorization over algebraic number fields are known, few are taught such general algorithms, as their use is mainly as part of the code of various computer algebra systems. This thesis provides a summary of one such algorithm, which the author has also fully implemented at https://github.com/Whirligig231/number-field-factorization, along with an analysis of the runtime of this algorithm. Let k be the product of the degrees of the adjoined elements used to form the algebraic number field in question, let s be the sum of the squares of these degrees, and let d be the degree of the polynomial to be factored; then the runtime of this algorithm is found to be O(d4sk2 + 2dd3).
    [Show full text]
  • Algebraic Number Theory
    Algebraic Number Theory William B. Hart Warwick Mathematics Institute Abstract. We give a short introduction to algebraic number theory. Algebraic number theory is the study of extension fields Q(α1; α2; : : : ; αn) of the rational numbers, known as algebraic number fields (sometimes number fields for short), in which each of the adjoined complex numbers αi is algebraic, i.e. the root of a polynomial with rational coefficients. Throughout this set of notes we use the notation Z[α1; α2; : : : ; αn] to denote the ring generated by the values αi. It is the smallest ring containing the integers Z and each of the αi. It can be described as the ring of all polynomial expressions in the αi with integer coefficients, i.e. the ring of all expressions built up from elements of Z and the complex numbers αi by finitely many applications of the arithmetic operations of addition and multiplication. The notation Q(α1; α2; : : : ; αn) denotes the field of all quotients of elements of Z[α1; α2; : : : ; αn] with nonzero denominator, i.e. the field of rational functions in the αi, with rational coefficients. It is the smallest field containing the rational numbers Q and all of the αi. It can be thought of as the field of all expressions built up from elements of Z and the numbers αi by finitely many applications of the arithmetic operations of addition, multiplication and division (excepting of course, divide by zero). 1 Algebraic numbers and integers A number α 2 C is called algebraic if it is the root of a monic polynomial n n−1 n−2 f(x) = x + an−1x + an−2x + ::: + a1x + a0 = 0 with rational coefficients ai.
    [Show full text]
  • The Nth Root of a Number Page 1
    Lecture Notes The nth Root of a Number page 1 Caution! Currently, square roots are dened differently in different textbooks. In conversations about mathematics, approach the concept with caution and rst make sure that everyone in the conversation uses the same denition of square roots. Denition: Let A be a non-negative number. Then the square root of A (notation: pA) is the non-negative number that, if squared, the result is A. If A is negative, then pA is undened. For example, consider p25. The square-root of 25 is a number, that, when we square, the result is 25. There are two such numbers, 5 and 5. The square root is dened to be the non-negative such number, and so p25 is 5. On the other hand, p 25 is undened, because there is no real number whose square, is negative. Example 1. Evaluate each of the given numerical expressions. a) p49 b) p49 c) p 49 d) p 49 Solution: a) p49 = 7 c) p 49 = unde ned b) p49 = 1 p49 = 1 7 = 7 d) p 49 = 1 p 49 = unde ned Square roots, when stretched over entire expressions, also function as grouping symbols. Example 2. Evaluate each of the following expressions. a) p25 p16 b) p25 16 c) p144 + 25 d) p144 + p25 Solution: a) p25 p16 = 5 4 = 1 c) p144 + 25 = p169 = 13 b) p25 16 = p9 = 3 d) p144 + p25 = 12 + 5 = 17 . Denition: Let A be any real number. Then the third root of A (notation: p3 A) is the number that, if raised to the third power, the result is A.
    [Show full text]
  • Math Symbol Tables
    APPENDIX A I Math symbol tables A.I Hebrew letters Type: Print: Type: Print: \aleph ~ \beth :J \daleth l \gimel J All symbols but \aleph need the amssymb package. 346 Appendix A A.2 Greek characters Type: Print: Type: Print: Type: Print: \alpha a \beta f3 \gamma 'Y \digamma F \delta b \epsilon E \varepsilon E \zeta ( \eta 'f/ \theta () \vartheta {) \iota ~ \kappa ,.. \varkappa x \lambda ,\ \mu /-l \nu v \xi ~ \pi 7r \varpi tv \rho p \varrho (} \sigma (J \varsigma <; \tau T \upsilon v \phi ¢ \varphi 'P \chi X \psi 'ljJ \omega w \digamma and \ varkappa require the amssymb package. Type: Print: Type: Print: \Gamma r \varGamma r \Delta L\ \varDelta L.\ \Theta e \varTheta e \Lambda A \varLambda A \Xi ~ \varXi ~ \Pi II \varPi II \Sigma 2: \varSigma E \Upsilon T \varUpsilon Y \Phi <I> \varPhi t[> \Psi III \varPsi 1ft \Omega n \varOmega D All symbols whose name begins with var need the amsmath package. Math symbol tables 347 A.3 Y1EX binary relations Type: Print: Type: Print: \in E \ni \leq < \geq >'" \11 « \gg \prec \succ \preceq \succeq \sim \cong \simeq \approx \equiv \doteq \subset c \supset \subseteq c \supseteq \sqsubseteq c \sqsupseteq \smile \frown \perp 1- \models F \mid I \parallel II \vdash f- \dashv -1 \propto <X \asymp \bowtie [Xl \sqsubset \sqsupset \Join The latter three symbols need the latexsym package. 348 Appendix A A.4 AMS binary relations Type: Print: Type: Print: \leqs1ant :::::; \geqs1ant ): \eqs1ant1ess :< \eqs1antgtr :::> \lesssim < \gtrsim > '" '" < > \lessapprox ~ \gtrapprox \approxeq ~ \lessdot <:: \gtrdot Y \111 «< \ggg »> \lessgtr S \gtr1ess Z < >- \lesseqgtr > \gtreq1ess < > < \gtreqq1ess \lesseqqgtr > < ~ \doteqdot --;- \eqcirc = .2..
    [Show full text]
  • Number Theory and Graph Theory Chapter 3 Arithmetic Functions And
    1 Number Theory and Graph Theory Chapter 3 Arithmetic functions and roots of unity By A. Satyanarayana Reddy Department of Mathematics Shiv Nadar University Uttar Pradesh, India E-mail: [email protected] 2 Module-4: nth roots of unity Objectives • Properties of nth roots of unity and primitive nth roots of unity. • Properties of Cyclotomic polynomials. Definition 1. Let n 2 N. Then, a complex number z is called 1. an nth root of unity if it satisfies the equation xn = 1, i.e., zn = 1. 2. a primitive nth root of unity if n is the smallest positive integer for which zn = 1. That is, zn = 1 but zk 6= 1 for any k;1 ≤ k ≤ n − 1. 2pi zn = exp( n ) is a primitive n-th root of unity. k • Note that zn , for 0 ≤ k ≤ n − 1, are the n distinct n-th roots of unity. • The nth roots of unity are located on the unit circle of the complex plane, and in that plane they form the vertices of an n-sided regular polygon with one vertex at (1;0) and centered at the origin. The following points are collected from the article Cyclotomy and cyclotomic polynomials by B.Sury, Resonance, 1999. 1. Cyclotomy - literally circle-cutting - was a puzzle begun more than 2000 years ago by the Greek geometers. In their pastime, they used two implements - a ruler to draw straight lines and a compass to draw circles. 2. The problem of cyclotomy was to divide the circumference of a circle into n equal parts using only these two implements.
    [Show full text]
  • Monic Polynomials in $ Z [X] $ with Roots in the Unit Disc
    MONIC POLYNOMIALS IN Z[x] WITH ROOTS IN THE UNIT DISC Pantelis A. Damianou A Theorem of Kronecker This note is motivated by an old result of Kronecker on monic polynomials with integer coefficients having all their roots in the unit disc. We call such polynomials Kronecker polynomials for short. Let k(n) denote the number of Kronecker polynomials of degree n. We describe a canonical form for such polynomials and use it to determine the sequence k(n), for small values of n. The first step is to show that the number of Kronecker polynomials of degree n is finite. This fact is included in the following theorem due to Kronecker [6]. See also [5] for a more accessible proof. The theorem actually gives more: the non-zero roots of such polynomials are on the boundary of the unit disc. We use this fact later on to show that these polynomials are essentially products of cyclotomic polynomials. Theorem 1 Let λ =06 be a root of a monic polynomial f(z) with integer coefficients. If all the roots of f(z) are in the unit disc {z ∈ C ||z| ≤ 1}, then |λ| =1. Proof Let n = degf. The set of all monic polynomials of degree n with integer coefficients having all their roots in the unit disc is finite. To see this, we write n n n 1 n 2 z + an 1z − + an 2z − + ··· + a0 = (z − zj) , − − j Y=1 where aj ∈ Z and zj are the roots of the polynomial. Using the fact that |zj| ≤ 1 we have: n |an 1| = |z1 + z2 + ··· + zn| ≤ n = − 1 n |an 2| = | zjzk| ≤ − j,k 2! .
    [Show full text]
  • Subclass Discriminant Nonnegative Matrix Factorization for Facial Image Analysis
    Pattern Recognition 45 (2012) 4080–4091 Contents lists available at SciVerse ScienceDirect Pattern Recognition journal homepage: www.elsevier.com/locate/pr Subclass discriminant Nonnegative Matrix Factorization for facial image analysis Symeon Nikitidis b,a, Anastasios Tefas b, Nikos Nikolaidis b,a, Ioannis Pitas b,a,n a Informatics and Telematics Institute, Center for Research and Technology, Hellas, Greece b Department of Informatics, Aristotle University of Thessaloniki, Greece article info abstract Article history: Nonnegative Matrix Factorization (NMF) is among the most popular subspace methods, widely used in Received 4 October 2011 a variety of image processing problems. Recently, a discriminant NMF method that incorporates Linear Received in revised form Discriminant Analysis inspired criteria has been proposed, which achieves an efficient decomposition of 21 March 2012 the provided data to its discriminant parts, thus enhancing classification performance. However, this Accepted 26 April 2012 approach possesses certain limitations, since it assumes that the underlying data distribution is Available online 16 May 2012 unimodal, which is often unrealistic. To remedy this limitation, we regard that data inside each class Keywords: have a multimodal distribution, thus forming clusters and use criteria inspired by Clustering based Nonnegative Matrix Factorization Discriminant Analysis. The proposed method incorporates appropriate discriminant constraints in the Subclass discriminant analysis NMF decomposition cost function in order to address the problem of finding discriminant projections Multiplicative updates that enhance class separability in the reduced dimensional projection space, while taking into account Facial expression recognition Face recognition subclass information. The developed algorithm has been applied for both facial expression and face recognition on three popular databases.
    [Show full text]
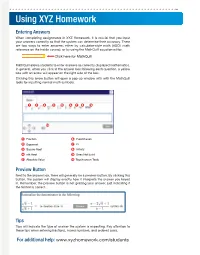
  • Using XYZ Homework
    Using XYZ Homework Entering Answers When completing assignments in XYZ Homework, it is crucial that you input your answers correctly so that the system can determine their accuracy. There are two ways to enter answers, either by calculator-style math (ASCII math reference on the inside covers), or by using the MathQuill equation editor. Click here for MathQuill MathQuill allows students to enter answers as correctly displayed mathematics. In general, when you click in the answer box following each question, a yellow box with an arrow will appear on the right side of the box. Clicking this arrow button will open a pop-up window with with the MathQuill tools for inputting normal math symbols. 1 2 3 4 5 6 7 8 9 10 1 Fraction 6 Parentheses 2 Exponent 7 Pi 3 Square Root 8 Infinity 4 nth Root 9 Does Not Exist 5 Absolute Value 10 Touchscreen Tools Preview Button Next to the answer box, there will generally be a preview button. By clicking this button, the system will display exactly how it interprets the answer you keyed in. Remember, the preview button is not grading your answer, just indicating if the format is correct. Tips Tips will indicate the type of answer the system is expecting. Pay attention to these tips when entering fractions, mixed numbers, and ordered pairs. For additional help: www.xyzhomework.com/students ASCII Math (Calculator Style) Entry Some question types require a mathematical expression or equation in the answer box. Because XYZ Homework follows order of operations, the use of proper grouping symbols is necessary.
    [Show full text]
  • Finite Fields: Further Properties
    Chapter 4 Finite fields: further properties 8 Roots of unity in finite fields In this section, we will generalize the concept of roots of unity (well-known for complex numbers) to the finite field setting, by considering the splitting field of the polynomial xn − 1. This has links with irreducible polynomials, and provides an effective way of obtaining primitive elements and hence representing finite fields. Definition 8.1 Let n ∈ N. The splitting field of xn − 1 over a field K is called the nth cyclotomic field over K and denoted by K(n). The roots of xn − 1 in K(n) are called the nth roots of unity over K and the set of all these roots is denoted by E(n). The following result, concerning the properties of E(n), holds for an arbitrary (not just a finite!) field K. Theorem 8.2 Let n ∈ N and K a field of characteristic p (where p may take the value 0 in this theorem). Then (i) If p ∤ n, then E(n) is a cyclic group of order n with respect to multiplication in K(n). (ii) If p | n, write n = mpe with positive integers m and e and p ∤ m. Then K(n) = K(m), E(n) = E(m) and the roots of xn − 1 are the m elements of E(m), each occurring with multiplicity pe. Proof. (i) The n = 1 case is trivial. For n ≥ 2, observe that xn − 1 and its derivative nxn−1 have no common roots; thus xn −1 cannot have multiple roots and hence E(n) has n elements.
    [Show full text]
  • Prime Factorization
    Prime Factorization Prime Number ­ A number with only two factors: ____ and itself Circle the prime numbers listed below 25 30 2 5 1 9 14 61 Composite Number ­ A number that has more than 2 factors List five examples of composite numbers What kind of number is 0? What kind of number is 1? Every human has a unique fingerprint. Similarly, every COMPOSITE number has a unique "factorprint" called __________________________ Prime Factorization ­ the factorization of a composite number into ____________ factors You can use a _________________ to find the prime factorization of any composite number. Ask yourself, "what Factorization two whole numbers 24 could I multiply together to equal the given number?" If the number is prime, do not put 1 x the number. Once you have all prime numbers, you are finished. Write your answer in exponential form. 24 Expanded Form (written as a multiplication of prime numbers) _______________________ Exponential Form (written with exponents) ________________________ Prime Factorization Ask yourself, "what two 36 numbers could I multiply together to equal the given number?" If the number is prime, do not put 1 x the number. Once you have all prime numbers, you are finished. Write your answer in both expanded and exponential forms. Prime Factorization Ask yourself, "what two 68 numbers could I multiply together to equal the given number?" If the number is prime, do not put 1 x the number. Once you have all prime numbers, you are finished. Write your answer in both expanded and exponential forms. Prime Factorization Ask yourself, "what two 120 numbers could I multiply together to equal the given number?" If the number is prime, do not put 1 x the number.
    [Show full text]
  • Performance and Difficulties of Students in Formulating and Solving Quadratic Equations with One Unknown* Makbule Gozde Didisa Gaziosmanpasa University
    ISSN 1303-0485 • eISSN 2148-7561 DOI 10.12738/estp.2015.4.2743 Received | December 1, 2014 Copyright © 2015 EDAM • http://www.estp.com.tr Accepted | April 17, 2015 Educational Sciences: Theory & Practice • 2015 August • 15(4) • 1137-1150 OnlineFirst | August 24, 2015 Performance and Difficulties of Students in Formulating and Solving Quadratic Equations with One Unknown* Makbule Gozde Didisa Gaziosmanpasa University Ayhan Kursat Erbasb Middle East Technical University Abstract This study attempts to investigate the performance of tenth-grade students in solving quadratic equations with one unknown, using symbolic equation and word-problem representations. The participants were 217 tenth-grade students, from three different public high schools. Data was collected through an open-ended questionnaire comprising eight symbolic equations and four word problems; furthermore, semi-structured interviews were conducted with sixteen of the students. In the data analysis, the percentage of the students’ correct, incorrect, blank, and incomplete responses was determined to obtain an overview of student performance in solving symbolic equations and word problems. In addition, the students’ written responses and interview data were qualitatively analyzed to determine the nature of the students’ difficulties in formulating and solving quadratic equations. The findings revealed that although students have difficulties in solving both symbolic quadratic equations and quadratic word problems, they performed better in the context of symbolic equations compared with word problems. Student difficulties in solving symbolic problems were mainly associated with arithmetic and algebraic manipulation errors. In the word problems, however, students had difficulties comprehending the context and were therefore unable to formulate the equation to be solved.
    [Show full text]
  • Algebraic Number Theory Summary of Notes
    Algebraic Number Theory summary of notes Robin Chapman 3 May 2000, revised 28 March 2004, corrected 4 January 2005 This is a summary of the 1999–2000 course on algebraic number the- ory. Proofs will generally be sketched rather than presented in detail. Also, examples will be very thin on the ground. I first learnt algebraic number theory from Stewart and Tall’s textbook Algebraic Number Theory (Chapman & Hall, 1979) (latest edition retitled Algebraic Number Theory and Fermat’s Last Theorem (A. K. Peters, 2002)) and these notes owe much to this book. I am indebted to Artur Costa Steiner for pointing out an error in an earlier version. 1 Algebraic numbers and integers We say that α ∈ C is an algebraic number if f(α) = 0 for some monic polynomial f ∈ Q[X]. We say that β ∈ C is an algebraic integer if g(α) = 0 for some monic polynomial g ∈ Z[X]. We let A and B denote the sets of algebraic numbers and algebraic integers respectively. Clearly B ⊆ A, Z ⊆ B and Q ⊆ A. Lemma 1.1 Let α ∈ A. Then there is β ∈ B and a nonzero m ∈ Z with α = β/m. Proof There is a monic polynomial f ∈ Q[X] with f(α) = 0. Let m be the product of the denominators of the coefficients of f. Then g = mf ∈ Z[X]. Pn j Write g = j=0 ajX . Then an = m. Now n n−1 X n−1+j j h(X) = m g(X/m) = m ajX j=0 1 is monic with integer coefficients (the only slightly problematical coefficient n −1 n−1 is that of X which equals m Am = 1).
    [Show full text]