Chapter 2 Knowledge-Based Methods and Simulation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

BeatingTheBookiesWithTheirOwnNumbers
Beating the bookies with their own numbers - and how the online sports betting market is rigged 1,2* 3* 4* Lisandro Kaunitz , Shenjun Zhong and Javier Kreiner 1- Research Center for Advanced Science and Technology, The University of Tokyo, Tokyo, Japan. 2- Progress Technologies Inc., Tokyo, Japan. 3- Monash Biomedical Imaging Center, Monash University, Melbourne, Australia. 4- Data Science department, CargoX, Sao Paulo, Brazil Corresponding authors: Lisandro Kaunitz / Javier Kreiner E-mail: [email protected] / [email protected] Abstract The online sports gambling industry employs teams of data analysts to build forecast models that turn the odds at sports games in their favour. While several betting strategies have been proposed to beat bookmakers, from expert prediction models and arbitrage strategies to odds bias exploitation, their returns have been inconsistent and it remains to be shown that a betting strategy can outperform the online sports betting market. We designed a strategy to beat football bookmakers with their own numbers. Instead of building a forecasting model to compete with bookmakers predictions, we exploited the probability information implicit in the odds publicly available in the marketplace to find bets with mispriced odds. Our strategy proved profitable -

(12) Patent Application Publication (10) Pub. No.: US 2012/0214567 A1 Snow (43) Pub
US 20120214567A1 (19) United States (12) Patent Application Publication (10) Pub. No.: US 2012/0214567 A1 Snow (43) Pub. Date: Aug. 23, 2012 (54) METHOD AND APPARATUS FORVARIANT Publication Classification OF TEXAS HOLDEM POKER (51) Int. Cl. A63F I3/00 (2006.01) (75) Inventor: Roger M. Snow, Las Vegas, NV A63F I/00 (2006.01) (US) (52) U.S. Cl. ........................................... 463/13; 273/292 57 ABSTRACT (73) Assignee: SHUFFLE MASTER, INC., Las (57) Vegas, NV (US) A variant game of Hold Empoker allows for rules of play of one or all of players being allowed to remain in game with an option of checking or making specific wagering amounts in (21) Appl. No.: 13/455.742 first play wagers, being limited in the size of Subsequent available play wagers or prohibited from making additional (22) Filed: Apr. 25, 2012 play wagers ifa first play wager has been made, being limited in the size of available laterplay wagers ifa first or earlier play Related U.S. Application Data wager has been made, and having the opportunity for at least two and as many as three or four distinct opportunities in the (62) Division of application No. 1 1/156.352, filed on Jun. stages in the play of a hand to be able to make one or more 17, 2005. play wagers. 110 Patent Application Publication Aug. 23, 2012 Sheet 1 of 10 US 2012/0214567 A1 Patent Application Publication Aug. 23, 2012 Sheet 2 of 10 US 2012/0214567 A1 a. s&Os Patent Application Publication Aug. 23, 2012 Sheet 3 of 10 US 2012/0214567 A1 Patent Application Publication Aug. -

Searching for Viable Betting Strategies in Gambling, with Consideration to Roulette
Searching for viable betting strategies in gambling, with consideration to Roulette Joseph Toninato UMD University Honors Capstone Project Introduction Gambling is one of the world’s oldest past times. Dice have been found in Egyptian tombs that are dated to be roughly 8000 years old. Since then, gambling has taken many different forms. Cards, dice, slots, wagers on sporting events, all of these fall under the umbrella of gambling. Whatever form it takes, all methods of gambling share the same structure. There is a game of chance, where people place wagers of money or assets or any multitude of things in the hopes of winning some amount of goods that are greater than their wager. Approximately 1.6 billion people worldwide reported gambling in some fashion in 2010. While many of these stated that they played the lottery, a large portion ventured into casinos. One of the most popular and iconic games in a casino is Roulette. This game is thought to originate from a perpetual motion machine invented in the 17th century, and played in its current form since before 1800. Roulette is a simple game in which a wheel is spun with numbered, colored, slots ranging from 0-36, and a double 0, or 00, in the American version. A ball is then allowed to spin around the outside of the wheel and fall into a random slot. This is the winning number. In addition, the numbers are colored either red or black, and the zero or zeros are colored green. A player may make one, or multiple, of many bets. -

NFL Betting Market Efficiency: Finding a Profitable Betting Strategy Spencer Anderson Skidmore College, [email protected]
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Skidmore College: Creative Matter Skidmore College Creative Matter Economics Student Theses and Capstone Projects Economics 2019 NFL Betting Market Efficiency: Finding a Profitable Betting Strategy Spencer Anderson Skidmore College, [email protected] Follow this and additional works at: https://creativematter.skidmore.edu/econ_studt_schol Part of the Economics Commons Recommended Citation Anderson, Spencer, "NFL Betting Market Efficiency: Finding a Profitable Betting Strategy" (2019). Economics Student Theses and Capstone Projects. 121. https://creativematter.skidmore.edu/econ_studt_schol/121 This Thesis is brought to you for free and open access by the Economics at Creative Matter. It has been accepted for inclusion in Economics Student Theses and Capstone Projects by an authorized administrator of Creative Matter. For more information, please contact [email protected]. NFL Betting Market Efficiency: Finding a Profitable Betting Strategy Spencer Anderson May 2, 2019 This thesis is submitted in partial fulfillment of the requirements for the course Senior Seminar (EC375), during the Spring Semester of 2018 While writing this thesis, I have not witnessed any wrongdoing, nor have I personally violated any conditions of the Skidmore College Honor Code. Name: Spencer Anderson Signature: __________________ Abstract This paper uses pregame spread data to attempt to analyze the efficiency of the NFL betting market. I look at hot hand betting, performance during prime-time games, home field advantage, and favorites to test for inefficiencies in the market, thereby uncovering a profitable betting strategy. Using OLS regression analysis, I find no evidence of a profitable betting strategy betting on teams on streaks or home underdogs. -

How to Win $250,000 a Year Playing Roulette! COPYRIGHT © 2017 by Silverthorne Publications Inc
Silverthorne Publications HHooww ttoo WWiinn $$225500,,000000 aa YYeeaarr PPllaayyiinngg RRoouulleettttee!! How to Win $250,000 a Year Playing Roulette! COPYRIGHT © 2017 by Silverthorne Publications Inc. All rights reserved. Except for brief passages used in legitimate reviews, no parts of this book may be reproduced or utilized in any form or by any means, electronic or mechanical, without the written permission of the publisher. Address all inquiries to the publisher: Silverthorne Publications, Inc. Address all inquiries to the publisher: 848 N. Rainbow Blvd., Suite 601 Las Vegas, Nevada 89107 USA World rights reserved. Web Sites: www.GamblersBookcase.com www.KillerGamblingStrategies.com www.KnockoutSystems.com YouTube: Channel: Gamblers Bookcase Published in the United States of America The material contained in this book is intended to inform and educate the reader and in no way represents an inducement to gamble legally or illegally How to Play Roulette Professionally & Make $250,000 a Year! © 2017 Silverthorne Publications 2 Table of Contents Introduction 3 How My Colleagues Work this System to Create Continuous 6 Windfalls for Themselves The Secret is in the Details 10 The Power of the CRB Betting Strategy 11 Ladies and Gentlemen, Place Your Bets 17 The Power of "Hit and Run" Gambling 20 Let's Compare Using the Double Cross Roulette Strategy With 22 Other Options You May Have Why Not Get Rich in the Dark? 25 What Do You Get If You Decide to Try Out the Double Cross 27 Roulette Strategy? Procedures and Bets in Roulette 29 The Player's Edge 40 Setting Up Your Winning Game Plan 45 Pumping Up Your Bankroll 52 Planning and Reaching Your Profit Goals 57 Maximizing Your Profits 61 Rules to Help Your Keep Your Winnings 63 A Day in the Life of a Double Cross Roulette Player 65 How to Play Roulette Professionally & Make $250,000 a Year! © 2017 Silverthorne Publications 3 Introduction There is now a proven way you can use to make very high profits with lower risk than investing in stocks, starting a business or just about any other method of making money. -

Approximating Game-Theoretic Optimal Strategies for Full-Scale Poker
Approximating Game-Theoretic Optimal Strategies for Full-scale Poker D. Billings, N. Burch, A. Davidson, R. Holte, J. Schaeffer, T. Schauenberg, and D. Szafron Department of Computing Science, University of Alberta Edmonton, Alberta, T6G 2E8, Canada Email: {darse,burch,davidson,holte,jonathan,terence,duane}@cs.ualberta.ca Abstract Due to the computational limitations involved, only simpli• fied poker variations have been solved in the past (e.g. [Kuhn, The computation of the first complete approxima• 1950; Sakaguchi and Sakai, 19921). While these are of the• tions of game-theoretic optimal strategies for full- oretical interest, the same methods are not feasible for real scale poker is addressed. Several abstraction tech• games, which are too large by many orders of magnitude niques are combined to represent the game of 2- ([Roller and Pfeffer, 1997J). player Texas Hold'em, having size O(1018), using 7 [Shi and Littman, 2001] investigated abstraction tech• closely related models each having size 0(1O ). niques to reduce the large search space and complexity of the Despite the reduction in size by a factor of 100 problem, using a simplified variant of poker. [Takusagawa, billion, the resulting models retain the key prop• 2000] created near-optimal strategies for the play of three erties and structure of the real game. Linear pro• specific Hold'em flops and betting sequences. [Selby, 1999] gramming solutions to the abstracted game are used computed an optimal solution for the abbreviated game of to create substantially improved poker-playing pro• 1 pre flop Hold em. grams, able to defeat strong human players and be Using new abstraction techniques, we have produced vi• competitive against world-class opponents. -
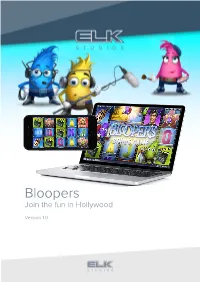
Bloopers Join the Fun in Hollywood
ELK BestStudios proudly in presents mobile the world premier of Bloopers Join the fun in Hollywood Version 1.0 Hollywood!… In Hollywood there are two kinds of people. The ones in front of the camera and the ones behind! But in the end, we know who it’s all about – it’s all about the Stars! ...Right? Bloopers is an entertaining 5 reel slot, designed for Mobile First with symbols covering 100% of the mobile screen. It is a fairly volatile game, aimed at a maximized mobile casino experience. The game features 243 paylines. The theme is based on a chaotic movie set, where the important final scene is just about to be shot. The two main movie stars (in their own respective eyes, of course the most important person on the set) are a couple of proper divas, constantly fighting to outshine each other. The set is also littered with a team of small, charming characters – the Bloopers. All with various jobs, such as sound technician or makeup artist, they constantly stumble and fumble about, making life hard for the divas. Throughout the game there are five di!erent Bloopers to be discovered. It is always in the favor of the player when they appear. Handing out Random Wilds, Sticky Wilds and Expanding Wilds, the Bloopers have every flavour of Wild covered. And added to all this extravaganza the player is also treated to Falling Reels and Extra Free Spins. All in all, an award-winning gaming experience! Action! Full Screen game experience Sound Tech – Random Sticky Wilds Fix-it – Optimizing Symbol Shu!es Make Up – Extra Free Spins Full Screen game experience Cutter – Falling Symbols Stunt Man – Expanding Wilds Exciting Base Game Betting Strategies Support for portrait mode BETTING STRATEGIES Are you looking for more action? Many players change the bet size based on the outcome of previous gameplay. -

An Artificial Intelligence Agent for Texas Hold'em Poker
AN ARTIFICIAL INTELL IGENCE AGENT FOR TEXAS HOLD’EM PO KER PATRICK MCCURLEY – 0 62 4 91 7 90 2 An Artificial Intelligence Agent for Texas Hold’em Poker I declare that this document represents my own work except where otherwise stated. Signed …………………………………………………………………………. 08/05/ 2009 Patrick McCurley – 062491790 Introduction 3 TABLE OF CONTENTS 1. Introduction ................................................................................................................................................................ 7 1.1 Problem Description...................................................................................................................................... 7 1.2 Aims and Objectives....................................................................................................................................... 7 1.3 Dissertation Outline ....................................................................................................................................... 8 1.4 Ethics .................................................................................................................................................................... 8 2 Background................................................................................................................................................................10 2.1 Artificial Intelligence and Poker .............................................................................................................10 2.1.1 Problem Domain Realization .........................................................................................................10 -

Mike Caro Caro's Book of Poker Tells
1 2 MIKE CARO CARO’S BOOK OF POKER TELLS THE PSICHOLOGY AND BODY LANGUAGE OF POKER 3 FREE GAMING NEWSLETTERS!!! www.cardozapub.com When you sign up for Avery Cardoza's online newsletters, you receive three for free: Avery Cardoza's Poker Newsletter, Avery Cardoza’s Gambling Newsletter and Avery Cardoza's Online Gaming Newsletter. Our newsletters are packed with tips, expert strategies, discounts, free money sign-up bonuses on online sites, pre-publication discounts, poker and gaming tournament news, schedules, and words of wisdom from the world's top experts, authorities, and World Champions. And what's best — it's FREE! Sign up now! www.cardozapub.com Mike Caro University of Poker Gaming and Life Strategy (MCU) merges Caro's own research with the collective wisdom of other great poker minds to form a one-of-a-kind learning center teaching poker strategy and psychology. In addition to instructional courses, MCU serves as a central force for popularizing poker, maintaining its integrity, and standardizing rules. Contact MCU's website at: UniversityofPoker.com. To join the mailing list: [email protected]. To contact the author: [email protected]. Cardoza Publishing is the foremost gaming and gambling publisher in the world with a library of more than 100 up-to-date and easy-to-read books and strategies. These authoritative works are written by the lop experts in their fields and with more than 7,500,000 books in print, represent the best-selling and most popular gaming books anywhere. FIRST CARDOZA EDITION First Printing February 2003 Second Printing July 2003 Third Printing October 2003 Fourth Printing March 2004 Fifth Printing October 2004 Library of Congress Catalog No: 2002106098 ISBN: 1-58042-082-6 This Cardoza edition is printed by special arrangement with Mike Caro University of Poker Press. -

Table of Contents
Table of Contents Introduction ....................................................................1 1. Basic Strategy .................................................................5 2. How the Game Has Changed ....................................10 3. Choosing Your Count—The “KISS” Principle .........19 4. Psychological Profile of a Winning High-Stakes Player ......................................27 5. The High Roller ............................................................42 6. Your P&L Statement—Penetration and Longevity ..............................................................56 7. The Ultimate Gambit with Stanford Wong .............79 8. Crazy Surrender .........................................................105 9. For Green-Chip Players ............................................ 117 10. Blackjack Debates ......................................................135 11. Amazing and Amusing Incidents (All True) .........153 12. On Guises and Disguises ..........................................166 13. Psychological Aspects of the Game ........................178 Burning the taBles in las Vegas 14. Understanding Casino Thinking .............................198 15. Tips & Tipoffs .............................................................218 16. Managing Risk ...........................................................266 17. International Play ......................................................275 18. On Maintaining Physical and Mental Fitness .......291 19. Epilogue ......................................................................313 -

Poker Phases: Draw, Stud and Hold’Em As Play-Forms of Capitalism
the author(s) 2011 ephemera articles ISSN 1473-2866 www.ephemeraweb.org theory & politics in organization volume 11(4): 450-465 Poker phases: Draw, Stud and Hold’Em as play-forms of capitalism Ole Bjerg abstract The subject of the article is the history of poker. It explores how different structural variations of the game have evolved and how different types of poker have been dominant at different periods in history. There are three main forms of poker: Draw, Stud and Hold’Em. In the article, it is demonstrated how the three forms emerge and become the most popular form of poker at three different periods in history. It identifies structural homologies between the historical development of poker and key elements in the manifestation of capitalism at different times in history. Introduction Poker is the laboratory of capitalism. (McDonald, 1950: 23) When we look at a piece of art, read a piece of literature, watch a film, or listen to a piece of music, it is commonplace to think of these as cultural expressions of the social and historical context in which they are created. Art, literature, film and music are readily recognized as mediums of the Zeitgeist. Poker and other gambling games are rarely thought of in the same fashion. At best, they are considered to be meaningless entertainment, at worst self-destructive vices. I would, however, argue that poker is a cultural expression in line with art, literature, film, etc. The sudden popularity of poker in recent years demonstrates the rich cultural resonance of the game. Poker is a game of money. -

How Egms Work
AGRC DISCUSSION PAPER 8 How electronic gambling machines work EGM structural characteristics Dr Charles Livingstone AUSTRALIAN GAMBLING RESEARCH CENTRE ┃ JULY 2017 AUSTRALIAN GAMBLING RESEARCH CENTRE Summary The purpose of this paper is to provide policy makers, regulators and others with information about key design characteristics of electronic gambling machines (EGMs). These characteristics include auditory and visual cues, “game maths”, and price and prize structure. They also include elements in the games that render them attractive to EGM users, and which appear to be associated with the establishment of persistent game utilisation or addiction. It is hoped that a better understanding of these characteristics will help policy makers and regulators to frame policies and interventions that will reduce harm to gamblers from EGM use. KEY MESSAGES Electronic gambling machines (EGMs) are computers utilising sophisticated techniques, designed to maximise spending and “time on device” per user. EGM designs very successfully employ psychological principals to maximise users’ bet sizes and machine usage. These characteristics have the effect of increasing the addictive potential of EGMs. Users of EGMs, and policy makers as well, are mostly not well informed about the way the machines work, or the complex “game maths” behind them. Internationally, Australian EGMs are known for their ability to maximise users’ spending and “time on device”, yet Australia has been slow to develop adequate policy responses to reduce harms. 2 | Australian Institute of Family Studies What are electronic gambling machines? Electronic gambling machines (EGMs), known colloquially as “pokies”, have their origins in older style lever-operated machines which spun a series of physical reels, on which were portrayed a number of winning symbols.