Efficient Node Overlap Removal Using a Proximity Stress Model
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Rachelle M. Scott
Rachelle M. Scott Associate Professor, Department of Religious Studies University of Tennessee, Knoxville, TN 37996 865-974-6688, [email protected] EDUCATION Northwestern University Ph.D. Religion 2002 Arizona State University M.A. Religious Studies 1994 Lawrence University B.A. Religious Studies 1992 PROFESSIONAL EXPERIENCE Associate Professor, University of Tennessee, 2010 – present Assistant Professor, University of Tennessee, 2003 – 2010 Lecturer, University of Tennessee, 2002 Instructor, Northwestern University, 2001 PUBLICATIONS “The Buddha’s Thumb, Nāga Legends, and Blessings of Health: Sacred Water and Religious Practice in Thailand,” Holy Wells and Sacred Springs: A Cross-Cultural Compendium, edited by Celeste Ray, Routledge, forthcoming (2019). “Religion, Prosperity, and Lottery Lore: The Linkage of New Religious Networks to Gambling Practices in Thailand,” New Religiosities, Modern Capitalism, and Moral Complexities in Southeast Asia, edited by Juliette Koning and Gwenaël Njoto-Feillard, Palgrave Macmillan, 2017. “Theravāda Buddhist Afterlife Beliefs and Funerary Practices,” Routledge Companion to Death and Dying, edited by Christopher M. Moreman, Routledge, 2017. “Contemporary Thai Buddhism,” Oxford Handbook of Contemporary Buddhism, edited by Michael Jerryson, Oxford University Press, 2016. “Pawinee Bunkhun: The Life of a Thai Buddhist Upasika,” Buddhists: Understanding Buddhism through the Lives of its Practitioners, edited by Todd Lewis, Oxford: Wiley- Blackwell, June 2014. “The Cultivation of Memory and Invention in Contemporary Thai Festivals,” Dharma World, 40, April-June 2013. “Buddhism, Miraculous Powers, and Sacred Biographies: Re-thinking the Stories of Theravāda Nuns,” Journal of the International Association of Buddhist Studies, 33: 2, Spring 2012. Nirvana for Sale?: Buddhism, Wealth, and the Dhammakāya Temple in Contemporary Thailand, Albany: State University of New York Press, September 2009. -

Most of Thailand Is Not Truly Buddhist John Lambert
1 Most Of Thailand is Not Truly Buddhist John Lambert February 4, 2012 True Buddhism or Not? If you have ever read anything about Thailand you may be led to believe that Thailand is a majority Theravada Buddhist nation. Some would say 95%. While it is true that the majority of Thai people would claim themselves to be Buddhist, the reality is that majority are not what the Thai would call “kreng sasanna” or fully devoted to their Buddhist faith. In fact, most Thai would have a wide variety of things that they respect, worship, or venerate in a typical day or week that would not be considered Buddhist at all. Most of these other things have to do with “spirits” or ghosts of people who are believed to have lived before in a past time. Daily Needs Each of these articles of daily worship and veneration mainly have to do with one of the felt needs of: Good Luck Prosperity Protection Here are a just a few of the main ones I see daily: Nang Kwak or แม่นางกวัก – She is the patron spirit deity of all sales people and businesses and can be seen in most every business in Thailand. You will see her sitting on a worship shelf with a glass of red liquid next to her beckoning passing potential customers to come in and make purchases. Her “cousin” Maneki Neko is a small white Japanese cat whose paw moves its paw back and forth to beckon customers. Pra Kruang or พระเครื่อง – These amulets contain a wide variety of images including those of past “super” monks believed to have magical powers to protect, give luck and prosperity to the people who proudly wear them . -

THAI CHARMS and AMULETS by Q>Hya Anuman Cflajadhon Acting President, Royal Lnstitztte
THAI CHARMS AND AMULETS by q>hya Anuman Cflajadhon Acting President, Royal lnstitztte Tbe belief in and use of charms and amulets as magical protec tion against dangers and misfortunes, and also to bring love, luck and power is a world-wide one. It is not confined to primitive races on! y, but also to be found among modern peoples of every nation and faith. In fact "the thought and practice of civilized peoples can not be cut off as with a knife from the underlying customs and beliefs which have played a determining part in shaping the resulting products, however much subsequent knowledge and ethical evaluation may have modified and transformed the earlier notions". 1 For this reason, every faith and religion has in one form or another certain cui ts and formulas, as inherited from the dim past and handed down from generation to generation, from the old belief of magic and superstition, which are paradoxically contrary to the real teaching of the religion's founder. This is inevitable; for the mass of humanity that forms the woof and warp of the woven fabric of faith of the great religions, is composed of many levels of culture. A.B. Griswold says in his "Doctrines and Reminders of Theravada Buddhism" that "within the Theravada there are two very different sorts of Buddhist rationalists and pious believers."2 This may be applied equally to other religions: there are always implicitly two sorts of believers within the same religion, the intellectuals and the pious people. It is with the latter that one can :find abundant phenomena of charms and amulets in belief and practice. -

Chiang-Mai-Uncovered.Pdf
Also by Derek Workman Inland Trips from the Costa Blanca Series COSTA BLANCA SOUTH AND MURCIA COSTA BLANCA NORTH CHIANG MAI VALENCIA NORTH VALENCIA SOUTH CASTELLON SMALL HOTELS AND INNS OF EASTERN SPAIN Morocco HIGH, RIDE AND HANDSOME A WHIRLWIND AROUND MOROCCO uncovered A DIFERENT LIFE REASONABLE PLANS CHIANG MAI UNCOVERED BETTER LATE THAN NEVER Recipe Books DINARI DELICIOUS KASBAH KITCHEN Eye On Photo Book Series EYE ON MOROCCO derek workman EYE ON VALENCIA EYE ON CHIANG MAI Written, photographed and designed by Derek Workman. No part of this book may be used, copied or distributed in any form whatsoever without the written permission of the author. Copyright © 2020 Derek Workman Cont A Work ents In Getting around Chiang Mai Page I have two modes of transport in Chiang Progress 6 Mai; a good pair of shoes and a bike Chiang Mai’s Stinky Market From well before dawn until late at night Page The stories in this book are a selection from the first five issues ofChiang 10 Muang Mai market buzzes, with a brief Mai uncovered, the result of many walks and cycle rides around this respite during the heat of the afternoon intriguing small city, and within a fifty kilometer radius of my home Wat Mae Kaet Noi near Chiang Mai Gate. Page The garden where retribution is more 16 than devine Within these pages you will find the unusual and unexpected, places A Passion For Everything that rarely get written about in guide books, and you will most likely find yourself one of the few foreign faces there – if there are any faces Page A museum of such joyous idiosyncrasy 20 that it makes most other museums seem there at all. -

<Articles>Constructing the Charisma of Khruba (Venerable Monks)
<Articles>Constructing the Charisma of Khruba (Venerable Title Monks) in Contemporary Thai Society Author(s) Pisith, Nasee Citation Southeast Asian Studies (2018), 7(2): 199-236 Issue Date 2018-08 URL http://hdl.handle.net/2433/234131 Right © Center for Southeast Asian Studies, Kyoto University Type Departmental Bulletin Paper Textversion publisher Kyoto University Southeast Asian Studies, Vol. 49, No. 2, September 2011 Constructing the Charisma of Khruba (Venerable Monks) in Contemporary Thai Society Pisith Nasee* Khruba (venerable monks) have consistently played a meaningful role in local Bud- dhist communities of Northern Thai culture for generations. While today’s khruba continue to represent themselves as followers of Khruba Siwichai and Lan Na Bud- dhism, in fact over the past three decades they have flourished by adopting hetero- geneous beliefs and practices in the context of declining influence of the sangha and popular Buddhism. In order to respond to social and cultural transformations and to fit in with different expectations of people, modern khruba construct charisma through different practices besides the obvious strictness in dhamma used to explain the source of khruba’s charisma in Lan Na Buddhist history. The ability to integrate local Buddhist traditions with the spirit of capitalism-consumerism and gain a large number of followers demonstrates that khruba is still a meaningful concept that plays a crucial role in modern Buddhist society, particularly in Thailand. By employ- ing concepts of charisma, production of translocalities, and popular Buddhism and prosperity religion, it can be argued that khruba is steeped in local knowledge, yet the concept has never been linear and static. -

Constructing the Charisma of Khruba (Venerable Monks) in Contemporary Thai Society
<Articles>Constructing the Charisma of Khruba (Venerable Title Monks) in Contemporary Thai Society Author(s) Pisith, Nasee Citation Southeast Asian Studies (2018), 7(2): 199-236 Issue Date 2018-08 URL http://hdl.handle.net/2433/234131 Right © Center for Southeast Asian Studies, Kyoto University Type Departmental Bulletin Paper Textversion publisher Kyoto University Southeast Asian Studies, Vol. 49, No. 2, September 2011 Constructing the Charisma of Khruba (Venerable Monks) in Contemporary Thai Society Pisith Nasee* Khruba (venerable monks) have consistently played a meaningful role in local Bud- dhist communities of Northern Thai culture for generations. While today’s khruba continue to represent themselves as followers of Khruba Siwichai and Lan Na Bud- dhism, in fact over the past three decades they have flourished by adopting hetero- geneous beliefs and practices in the context of declining influence of the sangha and popular Buddhism. In order to respond to social and cultural transformations and to fit in with different expectations of people, modern khruba construct charisma through different practices besides the obvious strictness in dhamma used to explain the source of khruba’s charisma in Lan Na Buddhist history. The ability to integrate local Buddhist traditions with the spirit of capitalism-consumerism and gain a large number of followers demonstrates that khruba is still a meaningful concept that plays a crucial role in modern Buddhist society, particularly in Thailand. By employ- ing concepts of charisma, production of translocalities, and popular Buddhism and prosperity religion, it can be argued that khruba is steeped in local knowledge, yet the concept has never been linear and static. -
Sponsored List for the Post of Lower Division Clerk, Rims, Imphal from Employment Exchanges
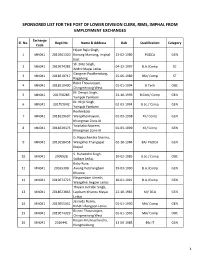
SPONSORED LIST FOR THE POST OF LOWER DIVISION CLERK, RIMS, IMPHAL FROM EMPLOYMENT EXCHANGES Exchange Sl. No. Regd No Name & Address Dob Qualification Category Code Hijam Rajiv Singh, 1 MN041 2019E61320 Konung Mamang, Imphal 12-02-1989 PGDCA GEN East Sh. Dilip Singh, 2 MN041 2019E74282 04-12-1997 B.A./Comp SC Andro Mayai Leikai Gangmei Pouthemlung, 3 MN041 2018E19717 25-06-1989 BSc/ Comp ST Ragailong Rohit Thounaojam, 4 MN041 2018E10490 01-01-1994 B.Tech OBC Chingmeirong West M. Devajit Singh, 5 MN041 2017E6285 24-10-1996 B.Com/ Comp GEN Yairipok Yambem M. Nirjit Singh, 6 MN041 2017E5042 02-03-1994 B.Sc./ Comp GEN Yairipok Yambem Roshinibala 7 MN041 2018E29697 Wangkheimayum, 01-03-1998 XII/ Comp GEN Khongman Zone-III Yaiphaba Naorem, 8 MN041 2018E29375 01-03-1999 XII/ Comp GEN Khongman Zone-III G. Nepuchandra Sharma, 9 MN041 2019E58458 Wangkhei Thangapat 02-10-1984 BA/ PGDCA GEN Mapal S. Huhedaho Singh, 10 MN041 2009S28 10-02-1985 B.Sc./ Comp OBC Soibam Leikai Baby Rose, 11 MN041 20165309 Awang Potshangbam 29-03-1990 B.A./Comp GEN Khunou Ningombam Umesh, 12 MN041 2019E74725 10-01-1991 B.A./Comp GEN Wangkhei Angom Leikai Thiyam Indrabir Singh, 13 MN041 2018E23865 Laipham Khunou Mayai 22-10-1983 XII/ DCA GEN Leikai Jasmida Narim, 14 MN041 2019E55341 01-01-1990 MA/ Comp GEN Kshetri Bangoon Leikai Bishan Thounaojam, 15 MN041 2019E74329 01-01-1995 MA/ Comp OBC Chingmeirong West Koijam Krishnachandra, 16 MN041 2010441 13-09-1985 BSc IT GEN Nongmeibung 1 Exchange Sl. No. Regd No Name & Address Dob Qualification Category Code Soraisham Tarunjit Meitei, 17 MN041 2017E5011 02-03-1990 ECE/ Comp OBC Khurai Sajor Leikai Kshetrimayum Dainesh 18 MN041 20136136 Meetei, 15-03-1994 MCA OBC Kongpal Chanam Leikai Laishram Melory Devi, 19 MN041 2019E72510 08-03-1988 BSc/ PGDCA GEN Chingmeirong East B. -

Spirit Mediumship in Thailand
Spirit Mediumship in Thailand A Performance Theory Approach R. Patamajorn SPIRIT MEDIUMSHIP IN THAILAND A Performance Theory Approach R. Patamajorn SPIRIT MEDIUMSHIP IN THAILAND A Performance Theory Approach A Thesis Submitted to The Institute for Ethnology Faculty of Behavioural and Cultural Studies The University of Heidelberg For The Degree of Doctor of Philosophy Under The Supervision and Guidance of Professor Dr. Klaus-Peter Köpping By R. Patamajorn (M.A. Sociology, M.A. Anthropology) August 2007 iv Contents Preface……………………………………………………………………... viii Introduction………………………………………………………………… 1 Part I Theoretical Considerations Chapter 1 Theoretical Issues……………………………………………… 16 1.1 Performance Theories ………………………………………………... 16 1.2 Spirit Possession……………………………………………………… 21 1.3 Gender Theories………………………………………………………. 25 1.4 Ethnicity………………………………………………………………. 29 Chapter 2 The Discussion of Spirit Mediumship Studies………………….. 34 2.1 General theoretical discussion………………………………………….. 34 2.2 Thai Possession Studies………………………………………………… 39 2.3 Comparative Summary of General Studies and Thai Cases……………. 44 Part II The General Phenomena Chapter 3 The Spirit Medium in Thai Society…………………………… 48 3.1 The History of Spirit Medium………………………………………… 48 3.2 Spirits and Séances ……………………… ………………………….. 55 3.3 Spirit possession in the Context of Social and Cultural Change……… 61 Chapter 4 The Phenomenon of Spirit Mediumship in Amphoe Muang Nakhon Pathom Province………………………………………………………. 66 Part III Theoretical Summary of Specific Case Studies Chapter 5 The Case Study Approach………………………………........... 80 5.1 How to become a spirit medium………………………………………. 80 v 5.2 Biography…………………………………………………………….. 95 Chapter 6 Spirit Medium in Ritual Action……………………………… 108 6.1 How to be a Successful Spirit Medium……………………… 108 6.1.2 Essential Factors…………………………………………… 108 6.1.2.1 Ability of Performance…………………………………… 109 6.1.2.1.1 Feature of Performance: The Depiction of Each Case Study 109 6.1.2.1.2 Comparison of the Similarities and Differences in Specific Case Studies…………………………………………………………. -

Religion a Human Phenomenon
RELIGION A HUMAN PHENOMENON XXth WORLd CONGREss INtERNAtIONAL AssOCIAtION of the HistORy Oforf the R ELIGIONs GENERAL PROGRAM UIRN vE sIty Of tORONtO ₁₅-₂₁ �ugust ₂₀₁₀ RELIGION A HUMAN PHENOMENON XXth WORLd CONGREss INtERNAtIONAL AssOCIAtION of the HistORy Oforf the R ELIGIONs GENERAL PROGRAM UIRN vE sIty Of tORONtO ₁₅-₂₁ �ugust ₂₀₁₀ The International Association for the History of Religions (IAHR) is a worldwide body of national and regional association committed to the scientific study of religion and religions. It was founded in 1950, although the first of the world congresses it supports was held in Paris in 1900. The world congresses are now held every five years. The IAHR is a member of the Conseil international de la philosophie et des sciences humaines (CIPSH) which functions under the auspices of UNESCO. Sponsoring Bodies Honorary Congress Chair Canadian Society for the Study of Religion Professor Armin W. Geertz Société québécoise pour l’étude de la religion Aarhus University North American Association for the Study of Religion Congress Chair Sociedad Mexicana para el Estudio de las Religiones Professor Rosalind Hackett, University of Conseil International de la Philosopie Tennessee: President, IAHR et des Sciences Humaines Congress Directors Host Institutions Professor Donald Wiebe, Trinity College, University of Toronto, Director Institute for the Advanced Study of Religion, Toronto Professor Russell McCutcheon, University of Department and Centre for the Study of Religion Alabama, Associate Director University of Toronto Professor Abrahim Khan, University of Toronto, Associate Chair, Congress Secretariat TOC Preliminaries General Information Plenaries Papers/Panels Index Map TABLE OF CONTENTS Welcome from the President of IAHR ...................................................................................................................... 5 General Congress Information .................................................................................................................................. -

Efficient Node Overlap Removal Using a Proximity Stress Model
Efficient Node Overlap Removal Using a Proximity Stress Model Emden R. Gansner∗ and Yifan Hu⋆ AT&T Labs, Shannon Laboratory, 180 Park Ave., Florham Park, NJ 07932. Abstract. When drawing graphs whose nodes contain text or graphics, the non-trivial node sizes must be taken into account, either as part of the initial layout or as a post-processing step. The core problem is to avoid overlaps while retaining the structural information inherent in a layout using little additional area. This paper presents a new node overlap removal algorithm that does well by these measures. 1 Introduction Most existing symmetric graph layout algorithms treat nodes as points. In prac- tice, nodes usually contain labels or graphics that need to be displayed. Naively incorporating this can lead to nodes that overlap, causing information of one node to occlude that of others. If we assume that the original layout conveys significant aggregate information such as clusters, the goal of any layout that avoids overlaps should be to retain the “shape” of the layout based on point nodes. The simplest and, in some sense, the best solution is to scale up the drawing [23] while preserving the node size until the nodes no longer overlap. This has the advantage of preserving the shape of the layout exactly, but can lead to inconveniently large drawings. In general, overlap removal is typically a trade-off between preserving the shape and limiting the area, with scaling at one extreme. Many techniques to avoid overlapping nodes have been devised. One approach is to make the node size part of the model of the layout algorithm. -

Thesis.Pdf (6.951Mb)
Institutt for arkeologi og sosialantropologi Lotusen vokser i gjørme Perspektiver på kommersialiseringen av amuletter og bruken av penger i den thailandske buddhismen Frank Hansen SOA 3900 Masteroppgave i sosialantropologi, november 2013 Sammendrag Denne oppgaven er basert på et syv måneder langt feltarbeid i Thailand 2011/12. I teksten beskriver jeg empirisk produksjonsprosesser, bruk og utveksling av buddhistiske amuletter i Thailand og forklarer den kulturelle logikken som ligger til grunn for forestillingen om at disse innehar supernaturlig kraft. Hovedfokuset er imidlertid utvekslingen av disse amulettene. Jeg har argumentert for at det har foregått en sosial endring der amuletter har gått fra å være gaver fra munker til lekfolk til å bli varer i templenes utsalgsdisker. Økt fokus på penger i buddhistiske templer og salget av amuletter har ført til moralske evalueringer der noen hevder at thaibuddhismen er i en krise. Mine observasjoner fra buddhisttemplene gav imidlertid et bilde av en svært levende religion der både munker og lekfolk så ut til å hylle penger snarere enn å hate dem. Jeg har forsøkt å gripe og begripe spenningen mellom to tilnærminger til det å være buddhist i dagens Thailand. Jeg har sett nærmere på kritikken, men har også forsøkt å forstå hvorfor dagens thaibuddhisme har et slikt pengefokus. Med utgangspunkt i Bloch og Parry (1989) er hovedargumentet i oppgaven at pengenes moralitet må fortås i lys av to transaksjonelle ordener. For på ene siden bedriver templene forretningsvirksomhet gjennom amulettsalg, men denne aktiviteten legitimeres ved at pengene benyttes for å bygge templer, skoler eller sykehus. Dermed transformeres og sosialiseres penger til noe som er sett som moralsk og positivt for samfunnet. -

The Sacred Geography of Bangkok's Markets
Volume 32.3 September 2008 631–42 International Journal of Urban and Regional Research DOI:10.1111/j.1468-2427.2008.00801.x The Sacred Geography of Bangkok’s Markets ARA WILSON Abstract Vernacular shrines pervade the markets of Bangkok, the capital of Thailand and a globalized city in Southeast Asia. Based on long-term ethnographic fieldwork in Bangkok, this article traces the history of cross-border flows and shifting political economic arrangements that remapped the sacred geography of the city. It considers the consolidation of a pantheon of enchanted figures into a modern ‘prosperity religion’that is practiced in commercial enterprises as well as in daily life across the country. Mapping the spiritual geography embodied in market shrines reveals changing mobilizations of local and transnational circuits of spiritual power in relation to the shifting national and transnational flows of material and cultural power. Vernacular shrines A mercantile metropolis, Bangkok overflows with shops, stalls, bazaars and shopping complexes, a plethora which has generated the commercial modernity of the capital of Thailand. Tucked into these ubiquitous venues for capitalist exchange are sacred spaces. Virtually all of Bangkok’s market sites include smaller or larger shrines hosting a range of enchanted figures. Ranging from a well-known elaborate shrine dedicated to Ganesh (the Erawan Shrine) to a small phallic lingam balanced on a noodle cart, such spiritual markers punctuate public and semi-public spaces of the city. Indeed, Bangkok’s energetic consumer economy acts as a stage for a transcultural pantheon of potent spiritual figures. Market shrines link economic and spiritual circuits in everyday practice and urban space.