DOCSLIB.ORG

Cipher Suites: Best Practices and Pitfalls

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Cipher Suites: Best Practices and Pitfalls Cipher Suite Practices and Pitfalls: An Overview of Cipher Suite Configuration and Pitfalls on BIG-IP PRESENTED BY: “A cipher suite is a named combination of authentication, encryption, message authentication code (MAC) and key exchange algorithms used to negotiate the security settings for a network connection using the Transport Layer Security (TLS) / Secure Sockets Layer (SSL) network protocol.” – Wikipedia When we talk about configuring ciphers on BIG-IP we’re really talking about configuring cipher suites. More specifically the configured list of cipher suites is a menu of options available to be negotiated. Each cipher suite specifies the key exchange algorithm, authentication algorithm, cipher, cipher mode, and MAC that will be used. I recommend reading K15194: Overview of the BIG-IP SSL/TLS cipher suite for more information. https://en.wikipedia.org/wiki/Cipher_suite Let’s consider this cipher suite: ECDHE-RSA-AES256-GCM-SHA384 Key Exchange Algorithm: ECDHE (Elliptic Curve Diffie-Hellman Ephemeral) Authentication Algorithm: RSA Cipher: AES256 (aka AES with a 256-bit key) Cipher Mode: GCM (Galois/Counter Mode) MAC: SHA384 (aka SHA-2 (Secure Hash Algorithm 2) with 384-bit hash) This is arguably the strongest cipher suite we have on BIG-IP at this time. What about this cipher suite: AES128-SHA Key Exchange Algorithm: RSA (Implied) – When it isn’t specified, presume RSA. Authentication Algorithm: RSA (Implied) – When it isn’t specified, presume RSA. Cipher: AES128 (aka AES with a 128-bit key) Cipher Mode: CBC (Cipher Block Chaining) (Implied) – When it isn’t specified, presume CBC. MAC: SHA1 (Secure Hash Algorithm 1; SHA-1 always produces a 160-bit hash.) This is to illustrate that the cipher suite may not always explicitly specify every parameter, but they’re still there. There are ‘default’ values that are fairly safe to presume when not otherwise specified. If an algorithm isn’t specified, it is RSA. That’s a safe bet. And if a cipher mode isn’t specified it is CBC. Always CBC. Note that all ciphers supported on BIG-IP are CBC mode except for AES-GCM and RC4. ALL. I stress this as it has been a recurring source of confusion. This presentation is really about cipher suite configuration and ciphers, and not the SSL/TLS protocol, so I won’t dive too deeply here. As a quick review of the difference between asymmetric key (aka public key) cryptography and symmetric key cryptography: With the asymmetric key you have two keys – Kpublic and Kprivate. Since you can openly share the public key there is no need to pre-share keys with anyone. The downside is these algorithms are computationally expensive. Key lengths for a common algorithm such as RSA are at least 1024-bit, and 2048-bit is really the minimally acceptable these days. Symmetric key has only Kprivate. Both ends use the same key, which poses the problem of key distribution. The advantage is higher performance; common key sizes are 128-bit or 256-bit. SSL/TLS uses both systems – the Key Exchange Algorithm is the public key system used to exchange the symmetric key. Examples: ECDHE, DHE, RSA, ECDH, ADH This is sometimes grouped in with the Key Exchange Algorithm – written as ‘ECDHE_RSA’ for example. But we’ll consider it as a separate component. This is the algorithm used in the SSL/TLS handshake for the server to sign (using the server’s private key) elements sent to the client in the negotiation. The client can authenticate them using the server’s public key. Examples include: RSA, ECDSA, DSS (aka DSA), and Anonymous. Anonymous means no authentication; this is generally bad. Using an ‘ADH’ cipher suite will cause this. More on this later when we talk about pitfalls. Note that when RSA is used for the key exchange authentication is inherent to the scheme so there really isn’t a separate authentication step. “In cryptography, a cipher (or cypher) is an algorithm for performing encryption or decryption—a series of well-defined steps that can be followed as a procedure. An alternative, less common term is encipherment. To encipher or encode is to convert information into cipher or code. In common parlance, 'cipher' is synonymous with 'code', as they are both a set of steps that encrypt a message; however, the concepts are distinct in cryptography, especially classical cryptography.” – Wikipedia Examples: DES (Data Encryption Standard), 3DES (Triple DES), AES (Advanced Encryption Standard), RC4 (Rivest Cipher 4), Camellia, RC6, RC2, Blowfish, Twofish, IDEA, SEED, GOST, Rijndael, Serpent, MARS, etc. For a little cryptography humor see: RFC2410: The NULL Encryption Algorithm and Its Use With IPsec https://en.wikipedia.org/wiki/Cipher All of the secrecy in encryption comes from the key that is used. Obtain the key and you can unlock the ciphertext. The cipher itself – the algorithm, source code, etc. – not only can be, but should be, openly available. History is full of examples of private cryptosystems failing due to weaknesses missed by their creators, while the most trusted ciphers were created via open processes (AES for example). Keys are of varying lengths and, generally speaking, the longer the key the more secure the encryption. DES only had 56-bits of key data, and thus is considered insecure. We label 3DES as 168-bit, but it is really only equivalent to 112-bit strength. (More on this at the end if there is time.) Newer ciphers, such as AES, often offer options – 128-bits, 192- bits, or 256-bits of key. Remember, a 256-bit key is far more than twice as strong as a 128-bit key. It is 2128 vs. 2256. Cipher mode is the mode of operation used by the cipher when encrypting plaintext into ciphertext, or decrypting ciphertext into plaintext. The most common mode is CBC – Cipher Block Chaining. In cipher block chaining the ciphertext from block n feeds into the process for block n+1 – the blocks are chained together. To steal an image from Wikipedia: https://en.wikipedia.org/wiki/Block_cipher_mode_of_operation#Cipher_Block_Chaining_.28CBC.29 As I said earlier, all ciphers on BIG-IP are CBC mode except for RC4 (the lone stream cipher, disabled by default starting in 11.6.0) and AES-GCM. AES-GCM was first introduced in 11.5.0, and it is only available for TLSv1.2 connections. GCM stands for Galois/Counter Mode, a more advanced mode of operation than CBC. In GCM the blocks are not chained together. GCM runs in an Authenticated Encryption with Associated Data (AEAD) mode which eliminates the separate per- message hashing step, therefore it can achieve much higher performance on a given HW platform than CBC. It is also immune to classes of attack that have harried CBC, such as padding (BEAST, Lucky 13, etc.) The main drawback to AES-GCM is that it was only added in the TLSv1.2 revision, so any older clients which don’t support TLSv1.2 cannot use it. Pronouncing Galois: https://youtu.be/bjHuJyGf-vE “A hash function is any function that can be used to map data of arbitrary size to data of fixed size. The values returned by a hash function are called hash values, hash codes, hash sums, or simply hashes. [snip] They are also useful in cryptography. A cryptographic hash function allows one to easily verify that some input data maps to a given hash value, but if the input data is unknown, it is deliberately difficult to reconstruct it (or equivalent alternatives) by knowing the stored hash value. This is used for assuring integrity of transmitted data, and is the building block for HMACs, which provide message authentication.” – Wikipedia In short, the MAC provides message integrity. Hash functions include MD5, SHA-1 (aka SHA), SHA-2 (aka SHA128, SHA256, & SHA384), and AEAD (Authenticated Encryption with Associated Data). MD5 has long since been rendered completely insecure and is deprecated. SHA-1 is now being ‘shamed’ by browsers as it is falling victim to advances in cryptographic attacks. It is encouraged to migrate to SHA-2 ASAP. https://en.wikipedia.org/wiki/Hash_function Now that we’ve covered what cipher suites are, lets look at where we use them. There are two distinct and separate areas where cipher suites are used – the host, or control plane, and tmm, or the data plane. On the control plane SSL/TLS is handled by OpenSSL and the configuration follows the standard OpenSSL configuration options. In tmm the cipher suites are configured in the Ciphers field of the Client SSL or Server SSL profiles. See K14783 & K14806, respectively. It is important to keep in mind that these are two different worlds with their own requirements and quirks. SSL/TLS on the control plane basically means httpd. This is the default in 12.0.0: tmsh list sys http ssl-ciphersuite sys httpd { ssl-ciphersuite DEFAULT:!aNULL:!eNULL:!LOW:!RC4:!MD5:!EXP } You can configure the cipher suite with ’tmsh modify sys http ssl-ciphersuite <value>’. Note that the default is not just ‘DEFAULT’, as it is in tmm. So what ciphers are actually supported? For that you want to run: openssl ciphers -v 'DEFAULT:!aNULL:!eNULL:!LOW:!RC4:!MD5:!EXP‘ That will list out all of the ciphers enabled by this configuration. Let’s see that on the next slide. openssl ciphers -v 'DEFAULT:!aNULL:!eNULL:!LOW:!RC4:!MD5:!EXP' ECDHE-RSA-AES256-GCM-SHA384 TLSv1.2 Kx=ECDH Au=RSA Enc=AESGCM(256) Mac=AEAD ECDHE-ECDSA-AES256-GCM-SHA384 TLSv1.2 Kx=ECDH Au=ECDSA Enc=AESGCM(256) Mac=AEAD ECDHE-RSA-AES256-SHA384 TLSv1.2 Kx=ECDH Au=RSA Enc=AES(256) Mac=SHA384 ECDHE-ECDSA-AES256-SHA384 TLSv1.2 Kx=ECDH Au=ECDSA Enc=AES(256) Mac=SHA384 ECDHE-RSA-AES256-SHA SSLv3 Kx=ECDH Au=RSA Enc=AES(256) Mac=SHA1 ECDHE-ECDSA-AES256-SHA SSLv3 Kx=ECDH Au=ECDSA Enc=AES(256)
Load more

Recommended publications
  • Camellia: a 128-Bit Block Cipher Suitable for Multiple Platforms
    gopyright x nd witsuishi iletri gorp ortion PHHHEPHHI g mel l iX e IPVEfit flo k gipher uitle for wultiple ltforms y z y uzumro eoki etsuyshikw wsyuki und z y z z witsuru wtsui hiho worii tunkoxkjim oshio okit y xipp on elegrph nd elephone gorp ortion IEI rikrino okD okosukD ungwD PQWEHVRU tpn fmroDkndDshihogdislFnttFoFjp z witsuishi iletri gorp ortion SEIEI yfunD umkurD ungwD PRUEVSHI tpn fihikwDmtsuiDjuneISDtokitgdissFislFmeloFoFjp er IFHX tuly IQD PHHH er PFHX eptemer PTD PHHI estrtF e present new IPVEit lo k ipher lled gmel liF gmelli supp orts IPVEit lo ksizend IPVED IWPED nd PSTEit keysD iFeF the sme interfe sp eitions s the edvned inryption tndrd @eiAF iieny on oth softE wre nd hrdwre pltforms is remrkle hrteristi of gmelli in ddition to its high level of seurityF st is onrmed tht gmelli provides strong seurity ginst dierentil nd liner ryptnlysisF gompred to the ei nlistsD iFeF weD gTD ijndelD erp entD nd woshD gmelli oers t lest omprle enryption sp eed in softwre nd hrdwreF en optimized implementtion of gmelE li in ssemly lnguge n enrypt on entiums s s @IFIQqrzA t the rte of RUI wits p er seondF sn dditionD distinguishing feture is its smll hrdwre designF e hrdwre implementtionD whih inludes enryptionD deryptionD nd the key shedule for IPVEit keysD o upies only VFIPu gtes using HFIV"m gwy esg lirryF his is in the smllest lss mong ll existing IPVEit lo k iphersF gopyright x nd witsuishi iletri gorp ortion PHHHEPHHI gontents I sntro dution I P hesign tionle Q PFI p Efuntion X X X X X X X X X X X X X X X X X X X X X X X X X
    [Show full text]
  • Zero Correlation Linear Cryptanalysis on LEA Family Ciphers
    Journal of Communications Vol. 11, No. 7, July 2016 Zero Correlation Linear Cryptanalysis on LEA Family Ciphers Kai Zhang, Jie Guan, and Bin Hu Information Science and Technology Institute, Zhengzhou 450000, China Email: [email protected]; [email protected]; [email protected] Abstract—In recent two years, zero correlation linear Zero correlation linear cryptanalysis was firstly cryptanalysis has shown its great potential in cryptanalysis and proposed by Andrey Bogdanov and Vicent Rijmen in it has proven to be effective against massive ciphers. LEA is a 2011 [2], [3]. Generally speaking, this cryptanalytic block cipher proposed by Deukjo Hong, who is the designer of method can be concluded as “use linear approximation of an ISO standard block cipher - HIGHT. This paper evaluates the probability 1/2 to eliminate the wrong key candidates”. security level on LEA family ciphers against zero correlation linear cryptanalysis. Firstly, we identify some 9-round zero However, in this basic model of zero correlation linear correlation linear hulls for LEA. Accordingly, we propose a cryptanalysis, the data complexity is about half of the full distinguishing attack on all variants of 9-round LEA family code book. The high data complexity greatly limits the ciphers. Then we propose the first zero correlation linear application of this new method. In FSE 2012, multiple cryptanalysis on 13-round LEA-192 and 14-round LEA-256. zero correlation linear cryptanalysis [4] was proposed For 13-round LEA-192, we propose a key recovery attack with which use multiple zero correlation linear approximations time complexity of 2131.30 13-round LEA encryptions, data to reduce the data complexity.
    [Show full text]
  • Cipher Support on a Citrix MPX/SDX (N3) Appliance
    Cipher support on a Citrix MPX/SDX (N3) appliance The following table lists the support for different ciphers on SSL entities, such as virtual server, frontend, backend, and internal services. On an SDX appliance, if an SSL chip is assigned to a VPX instance, the cipher support of an MPX appliance applies. Otherwise, the normal cipher support of a VPX instance applies. From release 10.5 build 56.22, NetScaler MPX appliances support full hardware optimization for all ciphers. In earlier releases, part of ECDHE/DHE cipher optimization was done in software. Use the 'show hardware' command to identify whether your appliance has N3 chips. > sh hardware Platform: NSMPX-22000 16*CPU+24*IX+12*E1K+2*E1K+4*CVM N3 2200100 Manufactured on: 8/19/2013 CPU: 2900MHZ Host Id: 1006665862 Serial no: ENUK6298FT Encoded serial no: ENUK6298FT Done How to read the table Unless a build number is specified, a cipher suite is supported for all builds in a release. Example • 10.5, 11.0, 11.1, 12.0, 12.1, 13.0: All builds of 10.5, 11.0, 11.1, 12.0, 12.1, 13.0, releases. • 11.1, 12.0, 12.1, 13.0: All builds of 11.1, 12.0, 12.1, 13.0 releases. • 10.5-53.x and later, 11.0, 11.1, 12.0, 12.1, 13.0: Build 53.x and later in release 10.5. All builds of 11.0, 11.1, 12.0, 12.1, 13.0 releases. • NA: not applicable. Ciphersuite Name Hex Wireshark Ciphersuite Name Builds Builds Code Supported Supported (frontend) (backend) TLS1-AES-256-CBC-SHA 0x0035 TLS_RSA_WITH_AES_256_CB 10.5, 11.0, 10.5, 11.0, C_SHA 11.1, 12.0, 11.1, 12.0, 12.1, 13.0 12.1, 13.0 TLS1-AES-128-CBC-SHA 0x002f
    [Show full text]
  • MD5 Collisions the Effect on Computer Forensics April 2006
    Paper MD5 Collisions The Effect on Computer Forensics April 2006 ACCESS DATA , ON YOUR RADAR MD5 Collisions: The Impact on Computer Forensics Hash functions are one of the basic building blocks of modern cryptography. They are used for everything from password verification to digital signatures. A hash function has three fundamental properties: • It must be able to easily convert digital information (i.e. a message) into a fixed length hash value. • It must be computationally impossible to derive any information about the input message from just the hash. • It must be computationally impossible to find two files to have the same hash. A collision is when you find two files to have the same hash. The research published by Wang, Feng, Lai and Yu demonstrated that MD5 fails this third requirement since they were able to generate two different messages that have the same hash. In computer forensics hash functions are important because they provide a means of identifying and classifying electronic evidence. Because hash functions play a critical role in evidence authentication, a judge and jury must be able trust the hash values to uniquely identify electronic evidence. A hash function is unreliable when you can find any two messages that have the same hash. Birthday Paradox The easiest method explaining a hash collision is through what is frequently referred to as the Birthday Paradox. How many people one the street would you have to ask before there is greater than 50% probability that one of those people will share your birthday (same day not the same year)? The answer is 183 (i.e.
    [Show full text]
  • Internet Engineering Task Force (IETF) S. Kanno Request for Comments: 6367 NTT Software Corporation Category: Informational M
    Internet Engineering Task Force (IETF) S. Kanno Request for Comments: 6367 NTT Software Corporation Category: Informational M. Kanda ISSN: 2070-1721 NTT September 2011 Addition of the Camellia Cipher Suites to Transport Layer Security (TLS) Abstract This document specifies forty-two cipher suites for the Transport Security Layer (TLS) protocol to support the Camellia encryption algorithm as a block cipher. Status of This Memo This document is not an Internet Standards Track specification; it is published for informational purposes. This document is a product of the Internet Engineering Task Force (IETF). It represents the consensus of the IETF community. It has received public review and has been approved for publication by the Internet Engineering Steering Group (IESG). Not all documents approved by the IESG are a candidate for any level of Internet Standard; see Section 2 of RFC 5741. Information about the current status of this document, any errata, and how to provide feedback on it may be obtained at http://www.rfc-editor.org/info/rfc6367. Copyright Notice Copyright (c) 2011 IETF Trust and the persons identified as the document authors. All rights reserved. This document is subject to BCP 78 and the IETF Trust's Legal Provisions Relating to IETF Documents (http://trustee.ietf.org/license-info) in effect on the date of publication of this document. Please review these documents carefully, as they describe your rights and restrictions with respect to this document. Code Components extracted from this document must include Simplified BSD License text as described in Section 4.e of the Trust Legal Provisions and are provided without warranty as described in the Simplified BSD License.
    [Show full text]
  • BLAKE2: Simpler, Smaller, Fast As MD5
    BLAKE2: simpler, smaller, fast as MD5 Jean-Philippe Aumasson1, Samuel Neves2, Zooko Wilcox-O'Hearn3, and Christian Winnerlein4 1 Kudelski Security, Switzerland [email protected] 2 University of Coimbra, Portugal [email protected] 3 Least Authority Enterprises, USA [email protected] 4 Ludwig Maximilian University of Munich, Germany [email protected] Abstract. We present the hash function BLAKE2, an improved version of the SHA-3 finalist BLAKE optimized for speed in software. Target applications include cloud storage, intrusion detection, or version control systems. BLAKE2 comes in two main flavors: BLAKE2b is optimized for 64-bit platforms, and BLAKE2s for smaller architectures. On 64- bit platforms, BLAKE2 is often faster than MD5, yet provides security similar to that of SHA-3: up to 256-bit collision resistance, immunity to length extension, indifferentiability from a random oracle, etc. We specify parallel versions BLAKE2bp and BLAKE2sp that are up to 4 and 8 times faster, by taking advantage of SIMD and/or multiple cores. BLAKE2 reduces the RAM requirements of BLAKE down to 168 bytes, making it smaller than any of the five SHA-3 finalists, and 32% smaller than BLAKE. Finally, BLAKE2 provides a comprehensive support for tree-hashing as well as keyed hashing (be it in sequential or tree mode). 1 Introduction The SHA-3 Competition succeeded in selecting a hash function that comple- ments SHA-2 and is much faster than SHA-2 in hardware [1]. There is nev- ertheless a demand for fast software hashing for applications such as integrity checking and deduplication in filesystems and cloud storage, host-based intrusion detection, version control systems, or secure boot schemes.
    [Show full text]
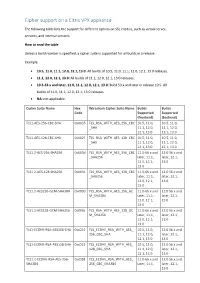
  • Cipher Support on a Citrix ADC VPX Appliance
    Cipher support on a Citrix VPX appliance The following table lists the support for different ciphers on SSL entities, such as virtual server, services, and internal services. How to read the table Unless a build number is specified, a cipher suite is supported for all builds in a release. Example • 10.5, 11.0, 11.1, 12.0, 12.1, 13.0: All builds of 10.5, 11.0, 11.1, 12.0, 12.1, 13.0 releases. • 11.1, 12.0, 12.1, 13.0: All builds of 11.1, 12.0, 12.1, 13.0 releases. • 10.5-53.x and later, 11.0, 11.1, 12.0, 12.1, 13.0: Build 53.x and later in release 10.5. All builds of 11.0, 11.1, 12.0, 12.1, 13.0 releases. • NA: not applicable. Cipher Suite Name Hex Wireshark Cipher Suite Name Builds Builds Code Supported Supported (frontend) (backend) TLS1-AES-256-CBC-SHA 0x0035 TLS_RSA_WITH_AES_256_CBC 10.5, 11.0, 10.5, 11.0, _SHA 11.1, 12.0, 11.1, 12.0, 12.1, 13.0 12.1, 13.0 TLS1-AES-128-CBC-SHA 0x002f TLS_RSA_WITH_AES_128_CBC 10.5, 11.0, 10.5, 11.0, _SHA 11.1, 12.0, 11.1, 12.0, 12.1, 13.0 12.1, 13.0 TLS1.2-AES-256-SHA256 0x003d TLS_RSA_WITH_AES_256_CBC 11.0-66.x and 12.0 56.x and _SHA256 later, 11.1, later, 12.1, 12.0, 12.1, 13.0 13.0 TLS1.2-AES-128-SHA256 0x003c TLS_RSA_WITH_AES_128_CBC 11.0-66.x and 12.0 56.x and _SHA256 later, 11.1, later, 12.1, 12.0, 12.1, 13.0 13.0 TLS1.2-AES256-GCM-SHA384 0x009d TLS_RSA_WITH_AES_256_GC 11.0-66.x and 12.0 56.x and M_SHA384 later, 11.1, later, 12.1, 12.0, 12.1, 13.0 13.0 TLS1.2-AES128-GCM-SHA256 0x009c TLS_RSA_WITH_AES_128_GC 11.0-66.x and 12.0 56.x and M_SHA256 later, 11.1, later, 12.1, 12.0, 12.1, 13.0 13.0 TLS1-ECDHE-RSA-AES256-SHA
    [Show full text]
  • The Missing Difference Problem, and Its Applications to Counter Mode
    The Missing Difference Problem, and its Applications to Counter Mode Encryption? Ga¨etanLeurent and Ferdinand Sibleyras Inria, France fgaetan.leurent,[email protected] Abstract. The counter mode (CTR) is a simple, efficient and widely used encryption mode using a block cipher. It comes with a security proof that guarantees no attacks up to the birthday bound (i.e. as long as the number of encrypted blocks σ satisfies σ 2n=2), and a matching attack that can distinguish plaintext/ciphertext pairs from random using about 2n=2 blocks of data. The main goal of this paper is to study attacks against the counter mode beyond this simple distinguisher. We focus on message recovery attacks, with realistic assumptions about the capabilities of an adversary, and evaluate the full time complexity of the attacks rather than just the query complexity. Our main result is an attack to recover a block of message with complexity O~(2n=2). This shows that the actual security of CTR is similar to that of CBC, where collision attacks are well known to reveal information about the message. To achieve this result, we study a simple algorithmic problem related to the security of the CTR mode: the missing difference problem. We give efficient algorithms for this problem in two practically relevant cases: where the missing difference is known to be in some linear subspace, and when the amount of data is higher than strictly required. As a further application, we show that the second algorithm can also be used to break some polynomial MACs such as GMAC and Poly1305, with a universal forgery attack with complexity O~(22n=3).
    [Show full text]
  • Poet Admits // Mute Cypher: Beam Search to Find Mutually Enciphering
    Poet Admits // Mute Cypher: Beam Search to find Mutually Enciphering Poetic Texts Cole Peterson and Alona Fyshe University of Victoria [email protected], [email protected] Abstract other English poem. In a sense, Bok¨ not only turns a microbe into a genetic book, he also engineers The Xenotext Experiment implants poetry into the microbe to be, in a sense, a poet. The organ- an extremophile’s DNA, and uses that DNA to generate new poetry in a protein form. ism’s molecular machinery powers this translation The molecular machinery of life requires that between the two texts, which, at a high level, is a these two poems encipher each other un- symmetric substitution cipher between the letters, der a symmetric substitution cipher. We and is described in more detail in Section 2. The search for ciphers which permit writing under two poems (the poet’s and the organism’s) must both the Xenotext constraints, incorporating ideas play by the rules we refer to as the Xenotext Con- from cipher-cracking algorithms, and using straints: n-gram data to assess a cipher’s “writabil- ity”. Our algorithm, Beam Verse, is a beam Each text is valid natural language. search which uses new heuristics to navigate • the cipher-space. We find thousands of ci- phers which score higher than successful ci- The substitution cipher function applied to one • phers used to write Xenotext constrained texts. text, results in the other text, and vice versa. In other words, the cipher function must be sym- 1 Introduction metric. For over a decade, poet Christian Bok¨ has been Whitespace characters (space, new line) enci- • working on The Xenotext (Bok,¨ 2008), a literary ex- pher themselves, and are the only characters al- periment which aims to insert poetry into the DNA lowed identity mappings.
    [Show full text]
  • Linear-XOR and Additive Checksums Don't Protect Damgård-Merkle
    Linear-XOR and Additive Checksums Don’t Protect Damg˚ard-Merkle Hashes from Generic Attacks Praveen Gauravaram1! and John Kelsey2 1 Technical University of Denmark (DTU), Denmark Queensland University of Technology (QUT), Australia. [email protected] 2 National Institute of Standards and Technology (NIST), USA [email protected] Abstract. We consider the security of Damg˚ard-Merkle variants which compute linear-XOR or additive checksums over message blocks, inter- mediate hash values, or both, and process these checksums in computing the final hash value. We show that these Damg˚ard-Merkle variants gain almost no security against generic attacks such as the long-message sec- ond preimage attacks of [10,21] and the herding attack of [9]. 1 Introduction The Damg˚ard-Merkle construction [3, 14] (DM construction in the rest of this article) provides a blueprint for building a cryptographic hash function, given a fixed-length input compression function; this blueprint is followed for nearly all widely-used hash functions. However, the past few years have seen two kinds of surprising results on hash functions, that have led to a flurry of research: 1. Generic attacks apply to the DM construction directly, and make few or no assumptions about the compression function. These attacks involve attacking a t-bit hash function with more than 2t/2 work, in order to violate some property other than collision resistance. Exam- ples of generic attacks are Joux multicollision [8], long-message second preimage attacks [10,21] and herding attack [9]. 2. Cryptanalytic attacks apply to the compression function of the hash function.
    [Show full text]
  • Camellia: a 128-Bit Block Cipher Suitable for Multiple Platforms – Design Andanalysis
    Camellia: A 128-Bit Block Cipher Suitable for Multiple Platforms – Design andAnalysis Kazumaro Aoki1, Tetsuya Ichikawa2, Masayuki Kanda1, Mitsuru Matsui2, Shiho Moriai1, Junko Nakajima2, and Toshio Tokita2 1 Nippon Telegraph and Telephone Corporation, 1-1 Hikarinooka, Yokosuka, Kanagawa, 239-0847Japan {maro,kanda,shiho}@isl.ntt.co.jp 2 Mitsubishi Electric Corporation, 5-1-1 Ofuna, Kamakura, Kanagawa, 247-8501 Japan {ichikawa,matsui,june15,tokita}@iss.isl.melco.co.jp Abstract. We present a new 128-bit block cipher called Camellia. Camellia supports 128-bit block size and 128-, 192-, and 256-bit keys, i.e., the same interface specifications as the Advanced Encryption Stan- dard (AES). Efficiency on both software and hardware platforms is a remarkable characteristic of Camellia in addition to its high level of se- curity. It is confirmed that Camellia provides strong security against differential and linear cryptanalyses. Compared to the AES finalists, i.e., MARS, RC6, Rijndael, Serpent, and Twofish, Camellia offers at least comparable encryption speed in software and hardware. An optimized implementation of Camellia in assembly language can encrypt on a Pen- tium III (800MHz) at the rate of more than 276 Mbits per second, which is much faster than the speed of an optimized DES implementation. In addition, a distinguishing feature is its small hardware design. The hard- ware design, which includes encryption and decryption and key schedule, occupies approximately 11K gates, which is the smallest among all ex- isting 128-bit block ciphers as far as we know. 1 Introduction This paper presents a 128-bit block cipher called Camellia, which was jointly developed by NTT and Mitsubishi Electric Corporation.
    [Show full text]
  • Steganography: Steganography Is a Type of Secret Communication Where the Existence of a Message Is Concealed
    Steganography: Steganography is a type of secret communication where the existence of a message is concealed. You can remember this by looking at the two parts of the word “stegano – graphy.” Both parts are of Greek origin. The Greek word steganos means “covered,” and the Greek word graphein means “to write.” Thus, a literal translation of steganography could be “covered writing.” The most simple form of steganography is hiding messages and images within larger pictures, such as the hidden symbols that can be found in the US dollar bill (can you find the spiders?). There are several different forms of steganography: Invisible Inks: Even in ancient times, invisible inks were used to hide messages. One example is using lemon juice on off-white parchment; only by holding the parchment up to a light will you be able to see the secret message: Music Cipher: In this method, notes on a scale correspond with letters in the alphabet. The message can be communicated through sheet music, or actual sound. Null Cipher: A null cipher is a type of hidden message where the real message is “camouflaged” in an innocent sounding message. A famous example of a null cipher is one sent by a German Spy in WWII: Apparently neutral’s protest is thoroughly discounted and ignored. Isman hit hard. Blockade issue affects pretext for embargo on by products, ejecting suets and vegetable oils. Taking the second letter in each word the following message emerges: Pershing sails from NY June 1. Digital Images: This fairly new method of steganography exploits the properties of digital images to hide messages.
    [Show full text]