3. Urban Modelling Cambridge Urban and Architectural Studies
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Lionel March Palladio's Villa Emo: the Golden Proportion Hypothesis Rebutted
Lionel Palladio’s Villa Emo: The Golden Proportion March Hypothesis Rebutted In a most thoughtful and persuasive paper Rachel Fletcher comes close to convincing that Palladio may well have made use of the ‘golden section’, or extreme and mean ratio, in the design of the Villa Emo at Fanzolo. What is surprising is that a visually gratifying result is so very wrong when tested by the numbers. Lionel March provides an arithmetic analysis of the dimensions provided by Palladio in the Quattro libri to reach new conclusions about Palladio’s design process. Not all that tempts your wand’ring eyes And heedless hearts, is lawful prize; Nor all that glisters, gold (Thomas Gray, Ode on the Death of a Favourite Cat) Historical grounding In a most thoughtful and persuasive paper [Fletcher 2000], Rachel Fletcher comes close to convincing that Palladio may well have made use of the ‘golden section’, or extreme and mean ratio, in the design of the Villa Emo at Fanzolo which was probably conceived and built during the decade 1555-1565. It is early in this period, 1556, that I dieci libri dell’archittetura di M. Vitruvio Pollionis traduitti et commentati ... by Daniele Barbaro was published by Francesco Marcolini in Venice and the collaboration of Palladio acknowledged. In the later Latin edition [Barbaro 1567], there are geometrical diagrams of the equilateral triangle, square and hexagon which evoke ratios involving 2 and 3, but there are no drawings of pentagons, or decagons, which might explicitly alert the perceptive reader to the extreme and mean proportion, 1 : I :: I : I2. -

White Paper-1
UCLA SYMPOSIUM ON DESIGN AND COMPUTATION A WHITE PAPER 1 _____________________________________________________________________________________________ SHAPE COMPUTATION at the University of California, Los Angeles A WHITE PAPER EXECUTIVE SUMMARY The UCLA Symposium on Design and Computation was convened by the Vice- Chancellor for Academic Affairs with the purpose of reviewing UCLA’s achievements in this field, of examining the prospects for interdisciplinary collaborations, and of making recommendations as to how such studies might best be accommodated on campus and promoted. The Symposium Chair was Professor Lionel March. The Symposium was charged with the preparation of a WHITE PAPER on Design and Computation at UCLA. • the Symposium reviewed UCLA’s leadership in this field over twenty-five years of research, teaching and practice, and the relationship of this work to developments in the field at other research and teaching institutions nationally and internationally; • the Symposium delineated the field of Design and Computation and agreed on a ‘vocabulary’ to forward the discussion. Some examples were proferred. It was generally agreed that the thrust of the work was methodological and related to ‘shape computation’ as applied analytically to promote the understanding of both natural phenomena and artifacts, and synthetically in the shaping of new products in a variety of markets; • the Symposium examined related methodologies in spatial analysis, and in configurational, or combinatorial synthesis, by way of comparison; • the Symposium divided itself into seven expert groups: an academic overview group, two groups focussed on theoretical developments and computer implementations, and four groups concerned with past applications and future potential - archaeology, geography and urban planning, architecture and design, engineering design. -

Feb 2 7 2004 Libraries Rotch
Architecture Theory 1960-1980. Emergence of a Computational Perspective by Altino Joso Magalhses Rocha Licenciatura in Architecture FAUTL, Lisbon (1992) M.Sc. in Advanced Architectural Design The Graduate School of Architecture Planning and Preservation Columbia University, New York. USA (1995) Submitted to the Department of Architecture, in Partial Fulfillment of the Requirements for the degree of Doctor of Philosophy in Architecture: Design and Computation at the MASSACHUSETTS INSTITUTE MASSACHUSETTS INSTITUTE OF TECHNOLOGY OF TECHNOLOGY February 2004 FEB 2 7 2004 @2004 Altino Joso Magalhaes Rocha All rights reserved LIBRARIES The author hereby grants to MIT permission to reproduce and to distribute publicly paper and electronic copies of this thesis document in whole or in part. Signature of Author......... Department of Architecture January 9, 2004 Ce rtifie d by ........................................ .... .... ..... ... William J. Mitchell Professor of Architecture ana Media Arts and Sciences Thesis Supervisor 0% A A Accepted by................................... .Stanford Anderson Chairman, Departmental Committee on Graduate Students Head, Department of Architecture ROTCH Doctoral Committee William J. Mitchell Professor of Architecture and Media Arts and Sciences George Stiny Professor of Design and Computation Michael Hays Eliot Noyes Professor of Architectural Theory at the Harvard University Graduate School of Design Architecture Theory 1960-1980. Emergence of a Computational Perspective by Altino Joao de Magalhaes Rocha Submitted to the Department of Architecture on January 9, 2004 in Partial Fulfilment of the Requirements for the degree of Doctor of Philosophy in Architecture: Design and Computation Abstract This thesis attempts to clarify the need for an appreciation of architecture theory within a computational architectural domain. It reveals and reflects upon some of the cultural, historical and technological contexts that influenced the emergence of a computational practice in architecture. -

Magdalene College Magazine 2017-18
magdalene college magdalene magdalene college magazine magazine No 62 No 62 2017–18 2017 –18 Designed and printed by The Lavenham Press. www.lavenhampress.co.uk MAGDALENE COLLEGE The Fellowship, October 2018 THE GOVERNING BODY 2013 MASTER: The Rt Revd & Rt Hon the Lord Williams of Oystermouth, PC, DD, Hon DCL (Oxford), FBA 1987 PRESIDENT: M E J Hughes, MA, PhD, Pepys Librarian, Director of Studies and University Affiliated Lecturer in English 1981 M A Carpenter, ScD, Professor of Mineralogy and Mineral Physics 1984 H A Chase, ScD, FREng, Director of Studies in Chemical Engineering and Emeritus Professor of Biochemical Engineering 1984 J R Patterson, MA, PhD, Praelector, Director of Studies in Classics and USL in Ancient History 1989 T Spencer, MA, PhD, Director of Studies in Geography and Professor of Coastal Dynamics 1990 B J Burchell, MA, and PhD (Warwick), Tutor, Joint Director of Studies in Human, Social and Political Science and Reader in Sociology 1990 S Martin, MA, PhD, Senior Tutor, Admissions Tutor (Undergraduates), Director of Studies and University Affiliated Lecturer in Mathematics 1992 K Patel, MA, MSc and PhD (Essex), Director of Studies in Economics & in Land Economy and UL in Property Finance 1993 T N Harper, MA, PhD, College Lecturer in History and Professor of Southeast Asian History (1990: Research Fellow) 1994 N G Jones, MA, LLM, PhD, Dean, Director of Studies in Law and Reader in English Legal History 1995 H Babinsky, MA and PhD (Cranfield), College Lecturer in Engineering and Professor of Aerodynamics 1996 P Dupree, -

Architectural Practice, Education and Research: on Learning from Cambridge
Architectural Practice, Education and Research: on Learning from Cambridge 64 docomomo 49 — 2013/2 Architectural Practice, Education and Research: on Learning from Cambridge docomomo49.indd 64 18/03/14 18:11 his paper reports firstly on the interrelated roles of architectural practice, education and research and focuses on the unique contribution of the Cambridge School in this area. The Tfollowing section presents the drawbacks derived from a research assessment exercise where architecture was no longer considered an academic subject to be developed in a research intensive university and, finally, concludes that architecture in Cambridge succeeded in spite of its problems, not in the absence of them, which suggests strongly that other European architectural schools can learn from it. By Mário Krüger stablished in 1912, the Cambridge School of Archi- Let us recall, in this respect, Martin’s words at the 1959 tecture celebrated last year its centenary within an Conference on Education in Architecture held at Oxford Eadverse economic climate for architectural educa- and organized by the Royal Institute of British Architects tion, practice and research all over Europe. (RIBA) where he raised the advantages of architecture If it is certain that the School in its early years can teaching in a university background (Martin, 1983): “The be “best interpreted as a combined school of architecture fundamental feature of education in architecture is that it and art history” (Saint, 2006), it is equally true that it had involves different types of knowledge. From the university its momentum when Leslie Martin was appointed its first point of view this raises two questions. -

Early Sources Informing Leon Battista Alberti's De Pictura
UNIVERSITY OF CALIFORNIA Los Angeles Alberti Before Florence: Early Sources Informing Leon Battista Alberti’s De Pictura A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Art History by Peter Francis Weller 2014 © Copyright by Peter Francis Weller 2014 ABSTRACT OF THE DISSERTATION Alberti Before Florence: Early Sources Informing Leon Battista Alberti’s De Pictura By Peter Francis Weller Doctor of Philosophy in Art History University of California, Los Angeles, 2014 Professor Charlene Villaseñor Black, Chair De pictura by Leon Battista Alberti (1404?-1472) is the earliest surviving treatise on visual art written in humanist Latin by an ostensible practitioner of painting. The book represents a definitive moment of cohesion between the two most conspicuous cultural developments of the early Renaissance, namely, humanism and the visual arts. This dissertation reconstructs the intellectual and visual environments in which Alberti moved before he entered Florence in the curia of Pope Eugenius IV in 1434, one year before the recorded date of completion of De pictura. For the two decades prior to his arrival in Florence, from 1414 to 1434, Alberti resided in Padua, Bologna, and Rome. Examination of specific textual and visual material in those cities – sources germane to Alberti’s humanist and visual development, and thus to the ideas put forth in De pictura – has been insubstantial. This dissertation will therefore present an investigation into the sources available to Alberti in Padua, Bologna and Rome, and will argue that this material helped to shape the prescriptions in Alberti’s canonical Renaissance tract. By more fully accounting for his intellectual and artistic progression before his arrival in Florence, this forensic reconstruction aims to fill a gap in our knowledge of Alberti’s formative years and thereby underline impact of his early career upon his development as an art theorist. -

An American Vision of Harmony: Geometric Proportions in Thomas Jefferson's Rotunda at the University of Virginia", Nexus Network Journal, Vol
American Vision of Harmony by Rachel Fletcher in the Nexus Network Journal vol. 5 no. 2 (Autumn 2003) 2/1/04 11:06 AM Abstract. Thomas Jefferson dedicated his later years to establishing the University of Virginia, believing that the availability of a public liberal education was essential to national prosperity and individual happiness. His design for the University stands as one of his greatest accomplishments and has been called "the proudest achievement of American architecture." Taking Jefferson's design drawings as a basis for study, this paper explores the possibility that he incorporated incommensurable geometric proportions in his designs for the Rotunda. Without actual drawings to illustrate specific geometric constructions, it cannot be said definitively that Jefferson utilized such proportions. But a comparative analysis between Jefferson's plans and Palladio's renderings of the Pantheon (Jefferson's primary design source) suggests that both designs developed from similar geometric techniques. NNJ Homepage Autumn 2003 index About the Author Search the NNJ An American Vision of Harmony: Geometric Proportions in Thomas Jefferson's Order Nexus books! Rotunda at the University of Virginia Research Articles Rachel Fletcher 113 Division St. The Geometer's Angle Great Barrington, MA 01230 USA Didactics …and in his hand Book Reviews He took the golden compasses, prepared In God's eternal store, to circumscribe Conference and Exhibit This universe, and all created things… Reports --Milton, Paradise Lost, Book VII, quoted in "Thoughts on English Prosody" by Thomas Jefferson to Chastellux, Readers' Queries October 1786 [Peterson 1984, 618]. The Virtual Library INTRODUCTION Thomas Jefferson died on July 4, 1826, fifty years after the adoption of the Declaration of American Submission Guidelines Independence, desiring in his 1826 inscription for his tombstone to be remembered as its author, the author of Virginia's Statute for Religious Freedom, and the father of the University of Virginia [Peterson 1984, 707]. -

EMERGENT SYMMETRIES: a Group Theoretic Analysis of an Exemplar of Late Modernism: the Smith House by Richard Meier
EMERGENT SYMMETRIES: A Group Theoretic Analysis of an Exemplar of Late Modernism: the Smith House by Richard Meier A Thesis Presented to The Academic Faculty By Edouard Denis Din In Partial Fulfillment of the Requirements for the Degree Doctoral of Philosophy in Architecture Georgia Institute of Technology August, 2008 Copyright © 2008 by Edouard Din All rights reserved. EMERGENT SYMMETRIES: A Group Theoretic Analysis of an Exemplar of Late Modernism: the Smith House by Richard Meier Approved by: Dr. Athanassios Economou, Chair College of Architecture – Georgia Institute of Technology Prof. Charles Eastman, Co-Chair College of Architecture – Georgia Institute of Technology Dr. Terry Knight School of Architecture – Massachusetts Institute of Technology Dr. John Peponis College of Architecture – Georgia Institute of Technology Dr. Ellen Yi-Luen Do College of Architecture – Georgia Institute of Technology Date Approved by Chair: July 1st, 2008 ‘The diverse elements of Classical Architecture are organized into coherent wholes by means of geometric systems of proportion. Precise rules of axiality, symmetry, or formal sequence govern the organization of the whole with hierarchical distribution.’ ‘What Modern Architecture brings out, is the complexification of these systems by algebrization of their geometric relations.’ W. J. Mitchell, ‘The Logic of Architecture’ iii ACKNOWLEDGEMENTS Even if I would like to acknowledge the many people who have patiently directed and channeled my thoughts from the beginning to the end of this journey, the intellectual roots of this work firmly stand on the shoulders of three giants. Dr. Cheikh Anta Diop, stimulated much of the thinking and energy powering of my lifelong research. Dr. Thomas Brylawski, my advisor during my tenure at UNC Department of Mathematics at Chapel Hill, definitely channeled my focus on the language of abstract thinking and the study of patterns. -
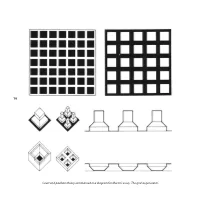
16 Court and Pavilion Theory Summarised in a Diagram For
16 Court and pavilion theory summarised in a diagram for Martin’s essay ‘The grid as generator’. An Outsider’s Re!ections PETER CAROLIN Peter Carolin worked with Colin St John Wilson from 1965 to 1980, from 1973 as a partner on the British Library. He was Technical and Practice Editor and then Editor of the Architects’ Journal from 1981 to 1989, and Professor of Architecture and Head of Department at Cambridge from 1989 to 2000. From 1995 to 2003 he was the founding editor of arq (Architectural Research Quarterly). Architectural research was almost non-existent during the department’s "rst half- century. In Andrew Saint’s history, “The Cambridge School of Architecture: A brief 17 history” (www.arct.cam.ac.uk), it features just three times: in the built work of the "rst professor, Edward Schroder Prior, and his studies of Gothic architecture (still remaining on the "rst year reading list when I came up in 1957); in the school’s short-lived attempt to engage in construction research during World War I; and in the failure, in the early 1930’s, of the "rst PhD candidate, Raymond McGrath, distracted from his research by his celebrated remodelling of Finella, a house in Queens Road. And there, as far as research was concerned, matters rested until, in 1956, the school’s "rst Professor of Architecture, Leslie Martin, arrived. (Prior had been Slade Professor of Art.) Martin was a practising architect who had headed the largest architectural o#ce in the world (at the London County Council), had a doctorate, and extensive experience in both teaching (at Manchester) and heading an architecture school (at Hull). -

Mathematics and Architecture Since 1960
Mathematics and Architecture since 1960 LIONEL MARCH “Mathematics and Architecture since 1960” — an impossibly tall order! In a short paper, I can only sketch an outline of work that I have had direct involvement with since the 1960s. I will touch upon some of my own work and work by some of my closest colleagues in architecture and urban studies.1 Much of this work is recorded in the academic research journal Environment and Planning B, of which I was appointed founding editor in 1974, and which, under the banner Planning and Design, is now in its 29th year.2 Many Environment and Planning B contributors have been colleagues “at a distance” whom I may have met on occasions, or not.3 Introduction A crude, but useful, distinction between mathematics and architecture is that the former tendss toward abstract generalizations ,r whe eas the latte r is concrete l y particular. In mathematics, take the simple rule of the so-called Pythagorean triangle – in a right triangle the squares on the sides sum to the square on the hypotenuse. Typical of the mathematical enterprise, the mathematician Pappus of Alexandria extended the rule to any triangle with any parallelograms on two sides (Figure 1): Figure 1. Pappus’s generalization of the Pythagoras Theorem where, for any triangle, the areas of the arbitrary black parallelograms on the left sum to the area of the appropriately constructed black parallelogram on the right It is not difficult to see that Pythagoras’s Theorem is just a very special case of Pappus. It is only a step further to arrive at what is known today as the cosine law. -

Lionel March (1934 – 2018)
Lionel March (1934 – 2018) Lionel March, scholar and artist, inspired generations of students and colleagues to combine the formal and the creative in planning and design. His contributions to theory and practice ranged from mathematics to painting, from computation to stage set design, from architectural history to architectural practice at its most daring; a modern Alberti. His career at the University of Cambridge in the Department of Architecture, in Canada at the Department of Systems Design in the University of Waterloo, in Milton Keynes at the Open University, in London at the Royal College of Art, and ultimately in Los Angeles at UCLA, was remarkable for his individual achievements, the research groups he established but most of all for his outstanding generosity in sharing ideas. Talking with Lionel made people think differently. His students and colleagues loved him for this generosity while university administrators were often exasperated by his mercurial mischievousness. His eye for the winner, in supporting new talent and new ideas in Design, was unrivalled. Early Years His early years growing up in Brighton and Hove were interrupted by a war time evacuation to Leeds where he remembered its black buildings, which must have seemed a marked contrast to the white stucco terraces at home. At grammar school in Brighton in his sixth form mathematics class, he wrote a paper constructing a new algebra. This eventually landed on Alan Turing’s desk at Manchester. The personal letters from Turing to Lionel are a terrifically clear explanation of the general mathematical concepts into which Lionel’s algebra fitted. You sense Alan Turing’s generosity in explaining beautifully, essential mathematical ideas as well as his urgent support for growing talent; something that Lionel did throughout his life. -

Lionel March Rudolph M. Schindler
Lionel March Rudolph M. Schindler Space Reference Frame, Modular Coordination and the “Row” While Rudolph Schindler’s “space reference frame” is becoming better known, its relationship to the “row” has only been recently investigated. The theory of the “row” counters traditional proportional notions, many of which are derived from the principle of geometric similitude: a principle which is mostly represented in architectural drawings by regulating lines and triangulation. Introduction The approach to architectural dimensioning taken by Rudolph Schindler (1887-1953) is described by Jin-Ho Park in a complimentary paper in this issue of the Nexus Network Journal [2003]. While Schindler’s “space reference frame” is becoming better known [Schindler 1946], its relationship to the “row” is only to be found in Park’s recent investigation. The theory of the “row” counters traditional proportional notions, many of which are derived from the principle of geometric similitude: a principle which is mostly represented in architectural drawings by regulating lines and triangulation. Park gives examples of this. Here, the simple mathematics of row theory is presented. A short background note concludes the paper. Space Reference Frame Mentally, Schindler [1946] conceived of a design within a three-dimensional integer lattice, or Cartesian grid: {(x. y. z) | for all positive integer values}. As an architect, Schindler had to choose a suitable module for his “unit.” In most of his designs, he chose 48 in. This module might be divided, Schindler argued, by 1/2, 1/3, 1/4, without losing a “feeling” for the dimensions. In fact, Schindler used 36 in., 24 in. and 12 in.