Primary Production Measurements: Methods
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Primer on Limnology, Second Edition
BIOLOGICAL PHYSICAL lake zones formation food webs variability primary producers light chlorophyll density stratification algal succession watersheds consumers and decomposers CHEMICAL general lake chemistry trophic status eutrophication dissolved oxygen nutrients ecoregions biological differences The following overview is taken from LAKE ECOLOGY OVERVIEW (Chapter 1, Horne, A.J. and C.R. Goldman. 1994. Limnology. 2nd edition. McGraw-Hill Co., New York, New York, USA.) Limnology is the study of fresh or saline waters contained within continental boundaries. Limnology and the closely related science of oceanography together cover all aquatic ecosystems. Although many limnologists are freshwater ecologists, physical, chemical, and engineering limnologists all participate in this branch of science. Limnology covers lakes, ponds, reservoirs, streams, rivers, wetlands, and estuaries, while oceanography covers the open sea. Limnology evolved into a distinct science only in the past two centuries, when improvements in microscopes, the invention of the silk plankton net, and improvements in the thermometer combined to show that lakes are complex ecological systems with distinct structures. Today, limnology plays a major role in water use and distribution as well as in wildlife habitat protection. Limnologists work on lake and reservoir management, water pollution control, and stream and river protection, artificial wetland construction, and fish and wildlife enhancement. An important goal of education in limnology is to increase the number of people who, although not full-time limnologists, can understand and apply its general concepts to a broad range of related disciplines. A primary goal of Water on the Web is to use these beautiful aquatic ecosystems to assist in the teaching of core physical, chemical, biological, and mathematical principles, as well as modern computer technology, while also improving our students' general understanding of water - the most fundamental substance necessary for sustaining life on our planet. -

Marine Primary Productivity: Measurements and Variability
Marine Primary Productivity: Measurements and Variability Matt Church Department of Oceanography MSB 612 Sunlight CO2 + 2H2OCH2O + O2 + H2O + heat Photosynthesis Gross Primary Production (GPP): The rate of organic carbon production via the reduction of CO2 inclusive of all respiratory losses. Net Primary Production (NPP): Gross primary production less photosynthetic respiration (RA): NPP = PN –RA Net Community Production (NCP): Gross primary production less all autotrophic and heterotrophic losses due to respiration (RA+H). NCP = PG –RA+H **If we are interested in carbon available for export or consumption by higher trophic levels, NCP is the key term. If we want to know how much total energy was captured by photosynthesis, we need to know GPP. What methods would you use to measure primary production in the sea? ∆O2 ∆CO2 ∆Organic matter Isotopic tracers of C and/or O2 What methods are most suitable for measuring aquatic primary production? • Typical rates of photosynthesis in the ocean range between 0.2-2 µmol C L-1 d-1 or -1 -1 0.3-3 µmol O2 L d -1, • Concentrations of DIC ~2000 µmol C L O2 ~220 µmol L-1, and TOC ~80-100 µmol L-1 • Analytical sensitivity of carbon and oxygen determinations: -1 –CO2 by coulometry = 1 µmol C L -1 –O2 by Winkler titration = 0.4 to 2 µmol O2 L –TOC by HTC = 2-4 µmol C L-1 **Measuring very small signals against large background pools** Commonly used methods for measuring aquatic photosynthesis • Changes in O2 concentrations – incubations (Gaarder and Gran 1927) and in situ dynamics. • CO2 assimilation: stable or radioisotopes of carbon (13C or 14C) – technique first applied by Steeman- Nielsen 1951. -

Seepage Chemistry Manual
RECLAMManagAingTWateIr iOn theNWest Report DSO-05-03 Seepage Chemistry Manual Dam Safety Technology Development Program U.S. Department of the Interior Bureau of Reclamation Technical Service Center Denver, Colorado December 2005 Form Approved REPORT DOCUMENTATION PAGE OMB No. 0704-0188 The public reporting burden for this collection of information is estimated to average 1 hour per response, including the time for reviewing instructions, searching existing data sources, gathering and maintaining the data needed, and completing and reviewing the collection of information. Send comments regarding this burden estimate or any other aspect of this collection of information, including suggestions for reducing the burden, to Department of Defense, Washington Headquarters Services, Directorate for Information Operations and Reports (0704-0188), 1215 Jefferson Davis Highway, Suite 1204, Arlington, VA 22202-4302. Respondents should be aware that notwithstanding any other provision of law, no person shall be subject to any penalty for failing to comply with a collection of information if it does not display a currently valid OMB control number. PLEASE DO NOT RETURN YOUR FORM TO THE ABOVE ADDRESS. 1. REPORT DATE (DD-MM-YYYY) 2. REPORT TYPE 3. DATES COVERED (From - To) 12-2005 Technical 4. TITLE AND SUBTITLE 5a. CONTRACT NUMBER Seepage Chemistry Manual 5b. GRANT NUMBER 5c. PROGRAM ELEMENT NUMBER 6. AUTHOR(S) 5d. PROJECT NUMBER Craft, Doug 5e. TASK NUMBER 5f. WORK UNIT NUMBER 7. PERFORMING ORGANIZATION NAME(S) AND ADDRESS(ES) 8. PERFORMING ORGANIZATION REPORT Bureau of Reclamation, Technical Service Center, D-8290, PO Box 25007, NUMBER Denver CO 80225 DSO-05-03 9. SPONSORING/MONITORING AGENCY NAME(S) AND ADDRESS(ES) 10. -

La Niña's Effect on the Primary Productivity of Phytoplankton in The
La Niña’s effect on the primary productivity of phytoplankton in the equatorial Pacific Stephen R. Pang University of Washington School of Oceanography, Box 357940 Seattle, WA 98195-7940 Email: [email protected] March 4th, 2011 Pang, La Niña’s Affect on Productivity Summary Phytoplankton form the base of the food chain in the world’s oceans; their declining or increasing populations can have major impacts on the abundance of other marine species. An important question to be asked is: how might a major oceanic change, such as a La Niña event, affect the primary productivity of phytoplankton communities? Primary productivity is a measure of the rate at which new organic matter is produced through photosynthesis by primary producers such as phytoplankton. The rate at which primary production occurs in the ocean is largely controlled by two major physical factors: solar radiation availability and the physical forces that bring nutrients up from deep water. This study wants to determine if the latter can be influenced by a La Niña event. A La Niña event is defined by lower sea surface temperatures in the equatorial Pacific. Typically, water in the ocean is characterized by warmer, less dense water residing on top of colder, denser water. The lower sea surface temperatures induced by a La Niña event could reduce the intensity of this layering, or stratification, in the upper water column. With the stratification weakened, water is more likely to move vertically throughout the water column. Water that is normally deeper, denser, and colder than the overlying water is now much more likely to move upwards toward the surface in a phenomenon that is called upwelling. -

SE 016 645 Handbook of Techniques and Guides for the Study Of
DOCUMENT RESUME ED 086 482 SE 016 645 TITLE Handbook of Techniques and Guides for the Study of the San Francisco Bay-Delta-Estuary Complex, Part 1. Monitoring Techniques for the Measurement of Physico-Chemical and Biological Parameters. INSTITUTION Alameda County School Dept., Hayward, Calif.; Contra Costa County Dept. of Education, Pleasant Hill, Calif. PUB DATE Feb 71 NOTE 120p. EDE'S PRICE MF-$0.65 HC-$6.58 DESCRIPTORS Biological Influences; Ecological Factors; Environmental Criteria; *Environmental Education; Environmental Research; *Guides; *Instructional Materials; *Marine Biology; Natural Sciences; Quality Control; Resource Materials; Water Pollution Control IDENTIFIERS *California; Project MER; San Francisco Bay ABSTRACT Project MER (Marine Ecology Research) is aimed at improving environmental education in the San Francisco Bay Area schools. As part of meeting this goal, it is hoped that students and teachers can see the results of their efforts being put to practical use. This guide is the first of a series produced to help the students and teachers gather data concerning the San Francisco Bay-Delta-Estuary Complex and to organize these data in a form that could be a contribution to the literature of science and serve as the groundwork upon which knowledgeable decisions about the environment could be based. Presented in this guide are techniques and procedures for measuring and evaluating the ecology of aquatic environment of the Bay. Chapter I deals with how physical and chemical factors affect the distribution of aquatic life. General information on the effect of a particular factor precedes a technical presentation on how to measure or evaluate that factor. The second chapter discusses techniques for studying the plankton population and the third liscusses techniques for studying bacterial populations. -

Determination of Dissolved Oxygen in Sea Water by Winkler Titration
Page 1 of 13 Determination of dissolved oxygen in sea water by Winkler titration 1. Scope and field of application This procedure describes a manual method based on the Winkler procedure for the determination of dissolved oxygen in sea water (Note 1).The method is suitable for the measurement of oceanic levels of oxygen (0–400 µmol·kg–1: Note 2) in uncontaminated sea water. (This method is unsuitable in sea water containing hydrogen sulfide.) 2. Definition The dissolved oxygen content of sea water is defined as the number of moles of dioxygen gas (O2) per kilogram of sea water. 3. Principle The basis of the Winkler procedure is that the oxygen in a sea water sample is made to oxidize iodide ion to iodine quantitatively (in the presence of an alkaline solution of manganese (II) ion); and the amount of iodine generated in this fashion is determined by titration with a standard thiosulfate solution. The end-point is located using starch as a visual indicator for the presence of iodine. The amount of oxygen present in the original sample can then be computed from the titer. The relevant chemical reactions occurring in the solution are: 2+ – → () Mn + 2OH Mn OH 2 (1) 1 A number of investigators have automated this procedure (using either changes in the absorption due to the triiodide ion to detect the end- point—see e.g. Williams & Jenkinson, 1982—or an amperometric technique—see e.g. Culberson & Huang, 1987). Such aproaches are potentially more convenient than the manual method detailed here. 2 –1 Significantly higher levels of O2—up to 535 µmol·kg —have been observed in cold waters with highplankton blooms. -

Full Text in Pdf Format
MARINE ECOLOGY PROGRESS SERIES Vol. 180: 23-36, 1999 Published May 3 Mar Ecol Prog Ser Microbial dynamics in coastal waters of East Antarctica: plankton production and respiration Carol R~binson'~~~*.**,Stephen D. ~rcher2r314r*, Peter J. le B. ~illiams' 'University of Wales Bangor, School of Ocean Sciences. Menai Bridge, Anglesey LL59 5EY. United Kingdom 'British Antarctic Survey, High Cross, Madingley Road, Cambridge CB3 OET, United Kingdom 3Department of Biology. University of Southampton. Medical and Biological Sciences Building, Bassett Crescent East, Southampton S016 7PX, United Kingdom 'In collaboration with the Australian Antarctic Division, Channel Highway, Kingston, Tasmania 7050, Australia ABSTRACT The rates of plankton community production and respiration were determined from in vitro changes in dissolved inorganic carbon and dissolved oxygen and the incorporation of NaH14C03 at a coastal site in East Antarctica between 16 December 1993 and 12 February 1994. The breakout of seasonal fast ice was associated with a succession of dominant phytoplankton from Cryptomonas to Phaeocystis to a d~atomassemblage. Gross production reached 33 mm01 C m-3 d-l and I4C incorpora- tion peaked at 24 mm01 C m-3 d-' on 23 January 1994, at the time of the chlorophyll a maximum (22 mg chl a m-3).Dark community respiration reached its maximum (13 mm01 C m-3 d-' ) 4 d later. Photosyn- thetic rates calculated from I4C incorporation were s~gnificantlylower (17 to 59%) than rates of gross production. The derivation of plankton processes from changes in both dissolved oxygen and dissolved inorganic carbon allowed the direct measurement of photosynthetic and respiratory quotients. A linear regression of all data gave a photosynthetic quotient of 1.33 + 0.23 and a respiratory quotient of 0.88 * 0.14. -

BOD Analysis: Basics and Particulars
BOD Analysis: Basics and Particulars George Bowman sponsored by: Inorganics Supervisor State Laboratory of Hygiene Rick Mealy Regional Certification Coordinator DNR-Laboratory Certification Disclaimer Any reference to product or company names does not constitute endorsement by the Wisconsin State Laboratory of Hygiene, the University of Wisconsin, or the Department of Natural Resources. April 2001 InformationInformation UpdatesUpdates Watch for…. Text highlighted like this indicates additional or updated information that is NOT on your handouts …be sure to annotate your handouts!!! Session Objectives Discuss Importance and Use of BOD Review Method and QC requirements Troubleshoot: QA/QC problems Identify Common Problems Experienced Troubleshoot: Common Problems Demonstrate: calibration, seeding, probe maintenance Troubleshoot: GGA and dilution water issues Discuss documentation required Provide necessary tools to pass audits Course Outline Overview Sampling/Sample Handling Equipment O2 Measurement Techniques Calibration Method Details Quality Control Troubleshooting Documentation BOD Basics What is it? • Bioassay technique • used to assess the relative strength of a waste −the amount of oxygen required −to stabilize it if discharged to a surface water. Significance of the BOD Test • Most commonly required test on WPDES and NPDES discharge permits. • Widely used in facility planning • Assess waste loading on surface waters • Characterized as the “Test everyone loves to hate” The test everyone loves to hate Rick George BOD Test: Limitations Test period is too long not good for process control Test is imprecise and unpredictable The test is simply not very easy - a lot of QC makes it time-consuming - can take years of experience to master it Cannot evaluate accuracy no universally accepted standard other than GGA accuracy at 200 ppm vs. -

Analytical Methods
United Nations Environment Programme Analytical Methods for Environmental Water Quality Global Environment Monitoring System with Analytical Methods for Environmental Water Quality Prepared and published by the United Nations Environment Programme Global Environment Monitoring System (GEMS)/Water Programme, in collaboration with the International Atomic Energy Agency. © 2004 United Nations Environment Programme Global Environment Monitoring System/Water Programme and International Atomic Energy Agency. This document may be reproduced in whole or in part in any form for educational or not-for-profit purposes, without special permission from the copyright holders, provided that acknowledgement of the source is made. GEMS/Water would appreciate receiving a copy of any publication that uses this reference guide as a source. No use of this publication may be made for resale or for any other commercial purpose whatsoever, without prior written permission from GEMS/Water and IAEA. The contents of this publication do not necessarily reflect the views of UNEP, of UNEP GEMS/Water Programme, or of IAEA, nor do they constitute any expression whatsoever concerning the legal status of any country, territory, city, of its authorities, or of the delineation of its frontiers or boundaries. A PDF version of this document may be downloaded from the GEMS/Water website at http://www.gemswater.org/quality_assurance/index-e.html UN GEMS/Water Programme Office c/o National Water Research Institute 867 Lakeshore Road Burlington, Ontario, L7R 4A6 CANADA website: http://www.gemswater.org tel: +1-905-336-4919 fax: +1-905-336-4582 email: [email protected] International Atomic Energy Agency Isotope Hydrology Section Wagramer Strasse 5, P.O. -

Oxygen Methods
SIO/STS/ODF OXYGEN ANALYSIS The Chemistry This system is called an oxygen titrator; in fact it is an iodine titrator, employing what has been a very standard procedure for the quantitative analysis of iodine for many years. Oxygen in a water sample cannot be stored because of its involvement in biological cycles and chemical reactions. Therefore, as soon as the sample is drawn, reagents are added so that the oxygen is used as an oxidizing agent to change manganese ions quantitatively from the +2 state to +4 in a basic (alkaline) medium. This is a stable condition for the manganese, and the samples may be kept for days, with proper precautions, or even weeks under very carefully controlled conditions, before finally running the analyses. When the sample is acidified in the presence of iodide ions, the +4 manganese has sufficient oxidizing potential to oxidize iodide (-1) to free iodine, which is then titrated by the addition of a known concentration of thiosulfate until all iodine is exhausted. The relevant chemical reactions occurring in the solution are: Mn2+ + 2OH- ! Mn(OH)2 Mn(OH)2 + 1/2O2 ! MnO(OH)2 Mn(OH)2 + 4H+ + 3I- ! Mn2+ + I3- + 3H2O I3- + 2S2O32- ! 3I- + S4O62- The concentration of the thiosulfate, and the amount needed to react with the iodine, are then used in the calculation of the amount of oxygen that was originally present. A precisely known oxidizing agent, KIO3, long used as a primary standard, is used to produce a known amount of iodine so that we can determine the exact strength or concentration of the thiosulfate solution. -
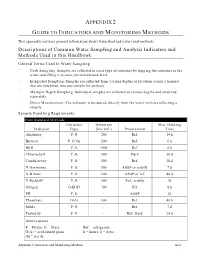
Descriptions of Common Water Sampling and Analysis Indicators and Methods Used in This Handbook
APPENDIX 2 GUIDE TO INDICATORS AND MONITORING METHODS This appendix contains general information about watershed indicators and methods. Descriptions of Common Water Sampling and Analysis Indicators and Methods Used in this Handbook General Terms Used In Water Sampling ¨ Grab Sampling: Samples are collected in some type of container by dipping the container in the water and filling it to some pre-determined level. ¨ Integrated Sampling: Samples are collected from various depths or locations across a transect that are combined into one sample for analysis. ¨ Multiple Depth Sampling: Individual samples are collected at various depths and analyzed separately. ¨ Direct Measurement: The indicator is measured directly from the water without collecting a sample. Sample Handling Requirments From Standard Methods Container Minimum Max. Holding Indicator Type Size (mL) Preservation Time Alkalinity P, G 200 Ref. 24 h Bacteria P, G (S) 200 Ref. 6 h BOD P, G 1000 Ref. 6 h Chlorophyll P, G 500 Dark 30 d Conductivity P, G 500 Ref. 28 d N-Ammonia P, G 500 ASAP or acidify 7 d N-Nitrate P, G 100 ASAP or ref. 48 h N-Kjeldahl P, G 500 Ref., acidify 7d Oxygen G-BOD 300 Fix 8 h PH P, G - ASAP 2h Phosphate G(A) 100 Ref. 48 h Solids P, G - Ref. 7 d Turbidity P, G - Ref., Dark 24 h Abbreviations P = Plastic, G = Glass Ref. = refrigerate G(A) = acid-rinsed glass h = hours, d = days (S) = sterile Appendix 2: Indicators and Monitoring Methods A2-1 General Terms Used In Water Analysis Methods This section describes the basic laboratory methods used to analyze water samples. -

Report on Method for Improved Gravimetric Winkler Titration
Report on method for improved, gravimetric Winkler titration Irja Helm Lauri Jalukse Ivo Leito* University of Tartu, Institute of Chemistry, 14a Ravila str, 50411 Tartu, Estonia Preparation of this report was supported by the European Metrology Research Programme (EMRP), project ENV05 "Metrology for ocean salinity and acidity". * Corresponding author: e-mail [email protected], phone +372 5 184 176, fax +372 7 375 261. 1 Table of Contents Abstract ........................................................................................................................... 3 Keywords ........................................................................................................................ 3 1. Introduction ................................................................................................................. 3 2. Experimental ............................................................................................................... 5 2.1 Materials ............................................................................................................... 5 2.2 Instrumentation and samples preparation ............................................................. 5 2.2.1 Changes in water density due to dissolved gases ........................................... 6 2.2.2 Preparation of air-saturated water .................................................................. 7 2.2.3 Concentration of oxygen air-saturated water ................................................. 9 2.2.4 Uncertainty of DO concentration in the