A Robust Statistical Distance Indicator for Planetary Nebulae
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Astronomie in Theorie Und Praxis 8. Auflage in Zwei Bänden Erik Wischnewski
Astronomie in Theorie und Praxis 8. Auflage in zwei Bänden Erik Wischnewski Inhaltsverzeichnis 1 Beobachtungen mit bloßem Auge 37 Motivation 37 Hilfsmittel 38 Drehbare Sternkarte Bücher und Atlanten Kataloge Planetariumssoftware Elektronischer Almanach Sternkarten 39 2 Atmosphäre der Erde 49 Aufbau 49 Atmosphärische Fenster 51 Warum der Himmel blau ist? 52 Extinktion 52 Extinktionsgleichung Photometrie Refraktion 55 Szintillationsrauschen 56 Angaben zur Beobachtung 57 Durchsicht Himmelshelligkeit Luftunruhe Beispiel einer Notiz Taupunkt 59 Solar-terrestrische Beziehungen 60 Klassifizierung der Flares Korrelation zur Fleckenrelativzahl Luftleuchten 62 Polarlichter 63 Nachtleuchtende Wolken 64 Haloerscheinungen 67 Formen Häufigkeit Beobachtung Photographie Grüner Strahl 69 Zodiakallicht 71 Dämmerung 72 Definition Purpurlicht Gegendämmerung Venusgürtel Erdschattenbogen 3 Optische Teleskope 75 Fernrohrtypen 76 Refraktoren Reflektoren Fokus Optische Fehler 82 Farbfehler Kugelgestaltsfehler Bildfeldwölbung Koma Astigmatismus Verzeichnung Bildverzerrungen Helligkeitsinhomogenität Objektive 86 Linsenobjektive Spiegelobjektive Vergütung Optische Qualitätsprüfung RC-Wert RGB-Chromasietest Okulare 97 Zusatzoptiken 100 Barlow-Linse Shapley-Linse Flattener Spezialokulare Spektroskopie Herschel-Prisma Fabry-Pérot-Interferometer Vergrößerung 103 Welche Vergrößerung ist die Beste? Blickfeld 105 Lichtstärke 106 Kontrast Dämmerungszahl Auflösungsvermögen 108 Strehl-Zahl Luftunruhe (Seeing) 112 Tubusseeing Kuppelseeing Gebäudeseeing Montierungen 113 Nachführfehler -
![Arxiv:1612.03165V3 [Astro-Ph.HE] 12 Sep 2017 – 2 –](https://docslib.b-cdn.net/cover/0040/arxiv-1612-03165v3-astro-ph-he-12-sep-2017-2-20040.webp)
Arxiv:1612.03165V3 [Astro-Ph.HE] 12 Sep 2017 – 2 –
The second catalog of flaring gamma-ray sources from the Fermi All-sky Variability Analysis S. Abdollahi1, M. Ackermann2, M. Ajello3;4, A. Albert5, L. Baldini6, J. Ballet7, G. Barbiellini8;9, D. Bastieri10;11, J. Becerra Gonzalez12;13, R. Bellazzini14, E. Bissaldi15, R. D. Blandford16, E. D. Bloom16, R. Bonino17;18, E. Bottacini16, J. Bregeon19, P. Bruel20, R. Buehler2;21, S. Buson12;22, R. A. Cameron16, M. Caragiulo23;15, P. A. Caraveo24, E. Cavazzuti25, C. Cecchi26;27, A. Chekhtman28, C. C. Cheung29, G. Chiaro11, S. Ciprini25;26, J. Conrad30;31;32, D. Costantin11, F. Costanza15, S. Cutini25;26, F. D'Ammando33;34, F. de Palma15;35, A. Desai3, R. Desiante17;36, S. W. Digel16, N. Di Lalla6, M. Di Mauro16, L. Di Venere23;15, B. Donaggio10, P. S. Drell16, C. Favuzzi23;15, S. J. Fegan20, E. C. Ferrara12, W. B. Focke16, A. Franckowiak2, Y. Fukazawa1, S. Funk37, P. Fusco23;15, F. Gargano15, D. Gasparrini25;26, N. Giglietto23;15, M. Giomi2;59, F. Giordano23;15, M. Giroletti33, T. Glanzman16, D. Green13;12, I. A. Grenier7, J. E. Grove29, L. Guillemot38;39, S. Guiriec12;22, E. Hays12, D. Horan20, T. Jogler40, G. J´ohannesson41, A. S. Johnson16, D. Kocevski12;42, M. Kuss14, G. La Mura11, S. Larsson43;31, L. Latronico17, J. Li44, F. Longo8;9, F. Loparco23;15, M. N. Lovellette29, P. Lubrano26, J. D. Magill13, S. Maldera17, A. Manfreda6, M. Mayer2, M. N. Mazziotta15, P. F. Michelson16, W. Mitthumsiri45, T. Mizuno46, M. E. Monzani16, A. Morselli47, I. V. Moskalenko16, M. Negro17;18, E. Nuss19, T. Ohsugi46, N. Omodei16, M. Orienti33, E. -

Is the Universe Expanding?: an Historical and Philosophical Perspective for Cosmologists Starting Anew
Western Michigan University ScholarWorks at WMU Master's Theses Graduate College 6-1996 Is the Universe Expanding?: An Historical and Philosophical Perspective for Cosmologists Starting Anew David A. Vlosak Follow this and additional works at: https://scholarworks.wmich.edu/masters_theses Part of the Cosmology, Relativity, and Gravity Commons Recommended Citation Vlosak, David A., "Is the Universe Expanding?: An Historical and Philosophical Perspective for Cosmologists Starting Anew" (1996). Master's Theses. 3474. https://scholarworks.wmich.edu/masters_theses/3474 This Masters Thesis-Open Access is brought to you for free and open access by the Graduate College at ScholarWorks at WMU. It has been accepted for inclusion in Master's Theses by an authorized administrator of ScholarWorks at WMU. For more information, please contact [email protected]. IS THEUN IVERSE EXPANDING?: AN HISTORICAL AND PHILOSOPHICAL PERSPECTIVE FOR COSMOLOGISTS STAR TING ANEW by David A Vlasak A Thesis Submitted to the Faculty of The Graduate College in partial fulfillment of the requirements forthe Degree of Master of Arts Department of Philosophy Western Michigan University Kalamazoo, Michigan June 1996 IS THE UNIVERSE EXPANDING?: AN HISTORICAL AND PHILOSOPHICAL PERSPECTIVE FOR COSMOLOGISTS STARTING ANEW David A Vlasak, M.A. Western Michigan University, 1996 This study addresses the problem of how scientists ought to go about resolving the current crisis in big bang cosmology. Although this problem can be addressed by scientists themselves at the level of their own practice, this study addresses it at the meta level by using the resources offered by philosophy of science. There are two ways to resolve the current crisis. -

Spectral Analysis of the Hybrid PG 1159-Type Central Stars of the Planetary Nebulae Abell 43 and NGC 7094
MNRAS 489, 1054–1071 (2019) doi:10.1093/mnras/stz1994 Advance Access publication 2019 July 25 Spectral analysis of the hybrid PG 1159-type central stars of the planetary nebulae Abell 43 and NGC 7094 L. Lobling¨ ,1‹ T. Rauch ,1 M. M. Miller Bertolami,2,3 H. Todt,4 F. Friederich,1 M. Ziegler,1 K. Werner 1 andJ.W.Kruk5 Downloaded from https://academic.oup.com/mnras/article-abstract/489/1/1054/5538811 by Macquarie University user on 29 August 2019 1Institute for Astronomy and Astrophysics, Kepler Center for Astro and Particle Physics, Eberhard Karls University, Sand 1, D-72076 Tubingen,¨ Germany 2Instituto de Astrof´ısica La Plata, CONICET-UNLP, Paseo del Bosque s/n, (B1900FWA) La Plata, Argentina 3Facultad de Ciencias Astronomicas´ y Geof´ısicas, UNLP, Paseo del Bosque s/n, (B1900FWA) La Plata, Argentina 4Institute of Physics and Astronomy, University of Potsdam, Karl-Liebknecht-Str. 24/25, D-14476 Potsdam, Germany 5NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA Accepted 2019 July 16. Received 2019 June 18; in original form 2019 April 30 ABSTRACT Stellar post asymptotic giant branch (post-AGB) evolution can be completely altered by a final thermal pulse (FTP) which may occur when the star is still leaving the AGB (AFTP), at the departure from the AGB at still constant luminosity (late TP, LTP) or after the entry to the white-dwarf cooling sequence (very late TP, VLTP). Then convection mixes the He- rich material with the H-rich envelope. According to stellar evolution models the result is a star with a surface composition of H ≈ 20 per cent by mass (AFTP), ≈ 1 per cent (LTP), or (almost) no H (VLTP). -
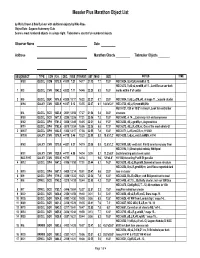
Messier Plus Marathon Text
Messier Plus Marathon Object List by Wally Brown & Bob Buckner with additional objects by Mike Roos Object Data - Saguaro Astronomy Club Score is most numbered objects in a single night. Tiebreaker is count of un-numbered objects Observer Name Date Address Marathon Obects __________ Tiebreaker Objects ________ SEQ OBJECT TYPE CON R.A. DEC. RISE TRANSIT SET MAG SIZE NOTES TIME M 53 GLOCL COM 1312.9 +1810 7:21 14:17 21:12 7.7 13.0' NGC 5024, !B,vC,iR,vvmbM,st 12.. NGC 5272, !!,eB,vL,vsmbM,st 11.., Lord Rosse-sev dark 1 M 3 GLOCL CVN 1342.2 +2822 7:11 14:46 22:20 6.3 18.0' marks within 5' of center 2 M 5 GLOCL SER 1518.5 +0205 10:17 16:22 22:27 5.7 23.0' NGC 5904, !!,vB,L,eCM,eRi, st mags 11...;superb cluster M 94 GALXY CVN 1250.9 +4107 5:12 13:55 22:37 8.1 14.4'x12.1' NGC 4736, vB,L,iR,vsvmbM,BN,r NGC 6121, Cl,8 or 10 B* in line,rrr, Look for central bar M 4 GLOCL SCO 1623.6 -2631 12:56 17:27 21:58 5.4 36.0' structure M 80 GLOCL SCO 1617.0 -2258 12:36 17:21 22:06 7.3 10.0' NGC 6093, st 14..., Extremely rich and compressed M 62 GLOCL OPH 1701.2 -3006 13:49 18:05 22:21 6.4 15.0' NGC 6266, vB,L,gmbM,rrr, Asymmetrical M 19 GLOCL OPH 1702.6 -2615 13:34 18:06 22:38 6.8 17.0' NGC 6273, vB,L,R,vCM,rrr, One of the most oblate GC 3 M 107 GLOCL OPH 1632.5 -1303 12:17 17:36 22:55 7.8 13.0' NGC 6171, L,vRi,vmC,R,rrr, H VI 40 M 106 GALXY CVN 1218.9 +4718 3:46 13:23 22:59 8.3 18.6'x7.2' NGC 4258, !,vB,vL,vmE0,sbMBN, H V 43 M 63 GALXY CVN 1315.8 +4201 5:31 14:19 23:08 8.5 12.6'x7.2' NGC 5055, BN, vsvB stell. -

Planetary Nebulae
Planetary Nebulae A planetary nebula is a kind of emission nebula consisting of an expanding, glowing shell of ionized gas ejected from old red giant stars late in their lives. The term "planetary nebula" is a misnomer that originated in the 1780s with astronomer William Herschel because when viewed through his telescope, these objects appeared to him to resemble the rounded shapes of planets. Herschel's name for these objects was popularly adopted and has not been changed. They are a relatively short-lived phenomenon, lasting a few tens of thousands of years, compared to a typical stellar lifetime of several billion years. The mechanism for formation of most planetary nebulae is thought to be the following: at the end of the star's life, during the red giant phase, the outer layers of the star are expelled by strong stellar winds. Eventually, after most of the red giant's atmosphere is dissipated, the exposed hot, luminous core emits ultraviolet radiation to ionize the ejected outer layers of the star. Absorbed ultraviolet light energizes the shell of nebulous gas around the central star, appearing as a bright colored planetary nebula at several discrete visible wavelengths. Planetary nebulae may play a crucial role in the chemical evolution of the Milky Way, returning material to the interstellar medium from stars where elements, the products of nucleosynthesis (such as carbon, nitrogen, oxygen and neon), have been created. Planetary nebulae are also observed in more distant galaxies, yielding useful information about their chemical abundances. In recent years, Hubble Space Telescope images have revealed many planetary nebulae to have extremely complex and varied morphologies. -

Two Rings but No Fellowship: Lotr 1 and Its Relation to Planetary Nebulae
Mon. Not. R. Astron. Soc. 000, 1–16 (2013) Printed 17 October 2018 (MN LATEX style file v2.2) Two rings but no fellowship: LoTr 1 and its relation to planetary nebulae possessing barium central stars. A.A. Tyndall1,2⋆, D. Jones2, H.M.J. Boffin2, B. Miszalski3,4, F. Faedi5, M. Lloyd1, J.A. L´opez6, S. Martell7, D. Pollacco5, and M. Santander-Garc´ıa8 1Jodrell Bank Centre for Astrophysics, School of Physics and Astronomy, University of Manchester, M13 9PL, UK 2European Southern Observatory, Alonso de C´ordova 3107, Casilla 19001, Santiago, Chile 3South African Astronomical Observatory, PO Box 9, Observatory 7935, South Africa 4Southern African Large Telescope. PO Box 9, Observatory 7935, South Africa 5Department of Physics, University of Warwick, CV4 7AL, UK 6Instituto de Astronom´ıa, Universidad Nacional Aut´onoma de M´exico, Ensenada, Baja California, C.P. 22800, Mexico 7Australian Astronomical Observatory, North Ryde, 2109 NSW, Australia 8Observatorio Astron´omico National, Madrid, and Centro de Astrobiolog´ıa, CSIC-INTA, Spain Accepted xxxx xxxxxxxx xx. Received xxxx xxxxxxxx xx; in original form xxxx xxxxxxxx xx ABSTRACT LoTr 1 is a planetary nebula thought to contain an intermediate-period binary central star system ( that is, a system with an orbital period, P, between 100 and, say, 1500 days). The system shows the signature of a K-type, rapidly rotating giant, and most likely constitutes an accretion-induced post-mass transfer system similar to other PNe such as LoTr 5, WeBo 1 and A70. Such systems represent rare opportunities to further the investigation into the formation of barium stars and intermediate period post-AGB systems – a formation process still far from being understood. -

Central Coast Astronomy Virtual Star Party January 16Th 7Pm Pacific
Central Coast Astronomy Virtual Star Party January 16th 7pm Pacific Welcome to our Virtual Star Gazing session! We’ll be focusing on objects you can see with binoculars or a small telescope, so after our session, you can simply walk outside, look up, and understand what you’re looking at. CCAS President Aurora Lipper and astronomer Kent Wallace will bring you a virtual “tour of the night sky” where you can discover, learn, and ask questions as we go along! All you need is an internet connection. You can use an iPad, laptop, computer or cell phone. When 7pm on Saturday night rolls around, click the link on our website to join our class. CentralCoastAstronomy.org/stargaze Before our session starts: Step 1: Download your free map of the night sky: SkyMaps.com They have it available for Northern and Southern hemispheres. Step 2: Print out this document and use it to take notes during our time on Saturday. This document highlights the objects we will focus on in our session together. Celestial Objects: Moon: The moon is 3 days past new, which is really good for star gazing. Be sure to look at the moon tonight with your naked eyes and/or binoculars! Mercury is rising into the western sky and may be a good target near the end of the month. Mars is up high but is shrinking in size as the weeks progress. *Image credit: all astrophotography images are courtesy of NASA unless otherwise noted. All planetarium images are courtesy of Stellarium. Central Coast Astronomy CentralCoastAstronomy.org Page 1 Main Focus for the Session: 1. -
![Arxiv:2009.04090V2 [Astro-Ph.GA] 14 Sep 2020](https://docslib.b-cdn.net/cover/4020/arxiv-2009-04090v2-astro-ph-ga-14-sep-2020-474020.webp)
Arxiv:2009.04090V2 [Astro-Ph.GA] 14 Sep 2020
Research in Astronomy and Astrophysics manuscript no. (LATEX: tikhonov˙Dorado.tex; printed on September 15, 2020; 1:01) Distance to the Dorado galaxy group N.A. Tikhonov1, O.A. Galazutdinova1 Special Astrophysical Observatory, Nizhnij Arkhyz, Karachai-Cherkessian Republic, Russia 369167; [email protected] Abstract Based on the archival images of the Hubble Space Telescope, stellar photometry of the brightest galaxies of the Dorado group:NGC 1433, NGC1533,NGC1566and NGC1672 was carried out. Red giants were found on the obtained CM diagrams and distances to the galaxies were measured using the TRGB method. The obtained values: 14.2±1.2, 15.1±0.9, 14.9 ± 1.0 and 15.9 ± 0.9 Mpc, show that all the named galaxies are located approximately at the same distances and form a scattered group with an average distance D = 15.0 Mpc. It was found that blue and red supergiants are visible in the hydrogen arm between the galaxies NGC1533 and IC2038, and form a ring structure in the lenticular galaxy NGC1533, at a distance of 3.6 kpc from the center. The high metallicity of these stars (Z = 0.02) indicates their origin from NGC1533 gas. Key words: groups of galaxies, Dorado group, stellar photometry of galaxies: TRGB- method, distances to galaxies, galaxies NGC1433, NGC 1533, NGC1566, NGC1672 1 INTRODUCTION arXiv:2009.04090v2 [astro-ph.GA] 14 Sep 2020 A concentration of galaxies of different types and luminosities can be observed in the southern constella- tion Dorado. Among them, Shobbrook (1966) identified 11 galaxies, which, in his opinion, constituted one group, which he called “Dorado”. -

Martin A. Guerrero Roncel Generated From: Editor CVN De FECYT Date of Document: 27/04/2019 V 1.4.0 Efb743b564d783564de108b1a8c5de25
Martin A. Guerrero Roncel Generated from: Editor CVN de FECYT Date of document: 27/04/2019 v 1.4.0 efb743b564d783564de108b1a8c5de25 This electronic file (PDF) has embedded CVN technology (CVN-XML). The CVN technology of this file allows you to export and import curricular data from and to any compatible data base. List of adapted databases available at: http://cvn.fecyt.es/ efb743b564d783564de108b1a8c5de25 Summary of CV This section describes briefly a summary of your career in science, academic and research; the main scientific and technological achievements and goals in your line of research in the medium -and long- term. It also includes other important aspects or peculiarities. Basic research in Astronomy and Astrophysics on the following topics: a) Formation and evolution of planetary nebulae. b) Interaction of evolved star stellar winds with circumstellar medium. c) Multi-wavelength study of interstellar bubbles. I got my PhD in 1995 on the spatially-resolved study of the chemical abundances of planetary nebulae (Univ. La Laguna, Instituto de Astrofísica de Canarias IAC, Tenerife, Spain). Then I was hired by the IAC as a member of the Support Astronomer group at Observatorio de El Roque de los Muchachos (ORM, La Palma, Spain). In 1999 I moved to the University of Illinois at Urbana-Champaign (USA) where I stayed until 2003, when I moved to the Instituto de Astrofísica de Andalucía (IAA) of the Spanish Consejo Superior de Investigaciones Científicas (CSIC) with a Ramón y Cajal tenure-track position. This tenure-track position moved into a permanent position (Científico Titular) in July 2006, being promoted into the next level (Investigador Científico) in March 2010. -

September 2020 BRAS Newsletter
A Neowise Comet 2020, photo by Ralf Rohner of Skypointer Photography Monthly Meeting September 14th at 7:00 PM, via Jitsi (Monthly meetings are on 2nd Mondays at Highland Road Park Observatory, temporarily during quarantine at meet.jit.si/BRASMeets). GUEST SPEAKER: NASA Michoud Assembly Facility Director, Robert Champion What's In This Issue? President’s Message Secretary's Summary Business Meeting Minutes Outreach Report Asteroid and Comet News Light Pollution Committee Report Globe at Night Member’s Corner –My Quest For A Dark Place, by Chris Carlton Astro-Photos by BRAS Members Messages from the HRPO REMOTE DISCUSSION Solar Viewing Plus Night Mercurian Elongation Spooky Sensation Great Martian Opposition Observing Notes: Aquila – The Eagle Like this newsletter? See PAST ISSUES online back to 2009 Visit us on Facebook – Baton Rouge Astronomical Society Baton Rouge Astronomical Society Newsletter, Night Visions Page 2 of 27 September 2020 President’s Message Welcome to September. You may have noticed that this newsletter is showing up a little bit later than usual, and it’s for good reason: release of the newsletter will now happen after the monthly business meeting so that we can have a chance to keep everybody up to date on the latest information. Sometimes, this will mean the newsletter shows up a couple of days late. But, the upshot is that you’ll now be able to see what we discussed at the recent business meeting and have time to digest it before our general meeting in case you want to give some feedback. Now that we’re on the new format, business meetings (and the oft neglected Light Pollution Committee Meeting), are going to start being open to all members of the club again by simply joining up in the respective chat rooms the Wednesday before the first Monday of the month—which I encourage people to do, especially if you have some ideas you want to see the club put into action. -

A Silicate Disk in the Heart of the Ant Which Reprocesses Most of the Stellar Light Emitted in Our Line Table 1
Astronomy & Astrophysics manuscript no. 8268 c ESO 2021 August 18, 2021 Letter to the Editor A silicate disk in the heart of the Ant O. Chesneau1, F. Lykou2, B. Balick3, E. Lagadec2, M. Matsuura4, N. Smith5, A. Spang1, S. Wolf6, and A.A. Zijlstra2,⋆ 1 Observatoire de la Cˆote d’Azur-CNRS-UMR 6203, Dept Gemini, Avenue Copernic, F-06130 Grasse, France e-mail: [email protected] 2 University of Manchester, School of Physics & Astronomy, P.O. Box 88, Manchester M60 1QD, UK 3 Astronomy Department, Box 351580, University of Washington, Seattle WA 98195 4 National Astronomical Observatory of Japan, Osawa 2-21-1, Mitaka, Tokyo 181-8588, Japan 5 Astronomy Department, University of California, 601 Campbell Hall, Berkeley CA 94720 6 Max-Planck-Institut f¨ur Astronomie, K¨onigstuhl 17, D-69117 Heidelberg, Germany Received ;accepted ABSTRACT Aims. We aim at getting high spatial resolution information on the dusty core of bipolar planetary nebulae to directly constrain the shaping process. Methods. We present observations of the dusty core of the extreme bipolar planetary nebula Menzel 3 (Mz 3, Hen 2-154, the Ant) taken with the mid-infrared interferometer MIDI/VLTI and the adaptive optics NACO/VLT. Results. The core of Mz 3 is clearly resolved with MIDI in the interferometric mode, whereas it is unresolved from the Ks to the N bands with single dish 8.2m observations on a scale ranging from 60 to 250mas. A striking dependence of the dust core size with the PA angle of the baselines is observed, that is highly suggestive of an edge-on disk whose major axis is perpendicular to the axis of the bipolar lobes.