An Efficient Subexpression Matching Method
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Release 0.11 Todd Gamblin
Spack Documentation Release 0.11 Todd Gamblin Feb 07, 2018 Basics 1 Feature Overview 3 1.1 Simple package installation.......................................3 1.2 Custom versions & configurations....................................3 1.3 Customize dependencies.........................................4 1.4 Non-destructive installs.........................................4 1.5 Packages can peacefully coexist.....................................4 1.6 Creating packages is easy........................................4 2 Getting Started 7 2.1 Prerequisites...............................................7 2.2 Installation................................................7 2.3 Compiler configuration..........................................9 2.4 Vendor-Specific Compiler Configuration................................ 13 2.5 System Packages............................................. 16 2.6 Utilities Configuration.......................................... 18 2.7 GPG Signing............................................... 20 2.8 Spack on Cray.............................................. 21 3 Basic Usage 25 3.1 Listing available packages........................................ 25 3.2 Installing and uninstalling........................................ 42 3.3 Seeing installed packages........................................ 44 3.4 Specs & dependencies.......................................... 46 3.5 Virtual dependencies........................................... 50 3.6 Extensions & Python support...................................... 53 3.7 Filesystem requirements........................................ -

Myths and Facts About the Efficient Implementation of Finite Automata and Lexical Analysis
Myths and Facts about the Efficient Implementation of Finite Automata and Lexical Analysis Klaus Brouwer, Wolfgang Gellerich and Erhard Ploedereder Department of Computer Science University of Stuttgart D-70565 Stuttgart Germany telephone: +49 / 711 / 7816 213; fax: -~49 / 711 / 7816 380 [email protected] keywords: Scanner, Lexical Analysis, Finite Automata, Run-time Efficiency Abstract. Finite automata and their application in lexical analysis play an important role in many parts of computer science and particularly in compiler constructions. We measured 12 scanners using different imple- mentation strategies and found that the execution time differed by a factor of 74. Our analysis of the algorithms as well as run-time statistics on cache misses and instruction frequency reveals substantive differences in code locality and certain kinds of overhead typical for specific im- plementation strategies. Some of the traditional statements on writing "fast" scanners could not be confirmed. Finally, we suggest an improved scanner generator. 1 Introduction and background Finite automata (FA) and regular languages in general are well understood and have found many applications in computer science, e.g., lexical analysis in com- pilers [23,3]. A number of different implementation strategies were developed [3,24] and there are many scanner generators translating regular specifications (RS) which consist of regular expressions (RE) with additional semantic actions into executable recognizers. Examples are Lex [3,25], flex [25,28], Alex [27], Aflex [31], REX [18,19], RE2C [5], and LexAgen [32]. There seem, however, to be only a few studies comparing the efficiency of different implementation strategies on today's computer architectures. -

Pipenightdreams Osgcal-Doc Mumudvb Mpg123-Alsa Tbb
pipenightdreams osgcal-doc mumudvb mpg123-alsa tbb-examples libgammu4-dbg gcc-4.1-doc snort-rules-default davical cutmp3 libevolution5.0-cil aspell-am python-gobject-doc openoffice.org-l10n-mn libc6-xen xserver-xorg trophy-data t38modem pioneers-console libnb-platform10-java libgtkglext1-ruby libboost-wave1.39-dev drgenius bfbtester libchromexvmcpro1 isdnutils-xtools ubuntuone-client openoffice.org2-math openoffice.org-l10n-lt lsb-cxx-ia32 kdeartwork-emoticons-kde4 wmpuzzle trafshow python-plplot lx-gdb link-monitor-applet libscm-dev liblog-agent-logger-perl libccrtp-doc libclass-throwable-perl kde-i18n-csb jack-jconv hamradio-menus coinor-libvol-doc msx-emulator bitbake nabi language-pack-gnome-zh libpaperg popularity-contest xracer-tools xfont-nexus opendrim-lmp-baseserver libvorbisfile-ruby liblinebreak-doc libgfcui-2.0-0c2a-dbg libblacs-mpi-dev dict-freedict-spa-eng blender-ogrexml aspell-da x11-apps openoffice.org-l10n-lv openoffice.org-l10n-nl pnmtopng libodbcinstq1 libhsqldb-java-doc libmono-addins-gui0.2-cil sg3-utils linux-backports-modules-alsa-2.6.31-19-generic yorick-yeti-gsl python-pymssql plasma-widget-cpuload mcpp gpsim-lcd cl-csv libhtml-clean-perl asterisk-dbg apt-dater-dbg libgnome-mag1-dev language-pack-gnome-yo python-crypto svn-autoreleasedeb sugar-terminal-activity mii-diag maria-doc libplexus-component-api-java-doc libhugs-hgl-bundled libchipcard-libgwenhywfar47-plugins libghc6-random-dev freefem3d ezmlm cakephp-scripts aspell-ar ara-byte not+sparc openoffice.org-l10n-nn linux-backports-modules-karmic-generic-pae -

Suse Linux Enterprise Server 10 Mail Scanning Gateway Build Guide
SuSE Linux Enterprise Server 10 Mail Scanning Gateway Build Guide Written By: Stephen Carter [email protected] Last Modified 9. May. 2007 Page 1 of 96 Table of Contents Due credit.......................................................................................................................................................4 Overview........................................................................................................................................................5 System Requirements.....................................................................................................................................6 SLES10 DVD............................................................................................................................................6 An existing e-mail server..........................................................................................................................6 A Pentium class PC...................................................................................................................................6 Internet Access..........................................................................................................................................6 Internet Firewall Modifications.................................................................................................................7 Installation Summary.....................................................................................................................................8 How -

Software Impacts RE2C: a Lexer Generator Based on Lookahead-TDFA
Software Impacts 6 (2020) 100027 Contents lists available at ScienceDirect Software Impacts journal homepage: www.journals.elsevier.com/software-impacts Original software publication RE2C: A lexer generator based on lookahead-TDFA Ulya Trofimovich Not affiliated to an organization ARTICLEINFO ABSTRACT Keywords: RE2C is a regular expression compiler: it transforms regular expressions into finite state machines and encodes Lexical analysis them as programs in the target language. At the core of RE2C is the lookahead-TDFA algorithm that allows Regular expressions it to perform fast and lightweight submatch extraction. This article describes the algorithm used in RE2C and Finite automata gives an example of TDFA construction. Code metadata Current code version 2.0 Permanent link to code/repository used for this code version https://github.com/SoftwareImpacts/SIMPAC-2020-29 Permanent link to reproducible capsule https://codeocean.com/capsule/6014695/tree/v1 Legal Code License Public domain Code versioning system used Git Software code languages, tools, and services used C++, Bison, RE2C (self-hosting) Compilation requirements, operating environments & dependencies OS: Linux, BSD, Nix/Guix, GNU Hurd, OS X, Windows, etc. Dependencies: C++ compiler, Bash, CMake or Autotools. Optional Bison and Docutils. Link to developer documentation/manual https://re2c.org Support email for questions [email protected] 1. Introduction submatch extraction needs only a partial derivation. Therefore it would be wasteful to perform full parsing, and a more specialized algorithm Regular expression engines can be divided in two categories: run- is needed that has overhead proportional to submatch detalization. For time libraries and lexer generators. Run-time libraries perform inter- an optimizing lexer generator like RE2C [1,2] it is important that the pretation or just-in-time compilation of regular expressions. -

Świat Parserów
Świat parserów Krzysztof Leszczyński Polska Grupa Użytkowników Linuxa [email protected] Streszczenie Pisząc oprogramowanie, stykamy się bardzo często z potrzebą analizy języków programowania. Niniejsza praca ma pomóc czytelnikowi zorientować się w gę- stwinie różnych mniej lub bardziej rozbudowanych generatorów parserów. 1. Wprowadzenie Zdecydowana większość używanych przez nas języków mieści się w klasie języków generowanych Języków programowania jest dzisiaj dużo, żeby nie gramatykami bezkontekstowymi. Czym innym jest powiedzieć za dużo. Ankieta, przeprowadzona wśród jednak zdefiniowanie gramatyki, a czym innym napi- koleżanek i kolegów zajmujących się programowa- sanie do niej parsera. A parsery musimy pisać dosyć niem, wykazała, że programiści twierdzą, że posłu- często. W przypadku języków opisu danych struktu- gują się przeciętnie pięcioma językami. Okazuje się, ralnych, pewną nadzieję dawało rozpowszechnienie że jest to przekonanie błędne. Indagowani przeze się języka XML. Nadzieja okazała się złudną, gdyż mnie, przyznają, że co prawda znają (lepiej lub go- XML naprawdę niewiele pomógł. Zamiast analizo- rzej) języki „podstawowe”: C, C++, jeden z P* wać mniej lub bardziej swobodny tekst, musimy ana- (Perl, Python, PHP), SQL, to jeszcze posługują się lizować tekst XML-owy pokrojony na leksemy XML- wieloma innymi językami, o których istnieniu nie owe. Analizy jest niewiele mniej niż w czasach przed- wiedzą; podobnie jak nie wiemy, że prawie cały czas XML-owych. mówimy prozą. Gdybyśmy policzyli liczbę rodzajów plików, które edytujemy, to różnych języków doli- Byłoby najlepiej, gdybyśmy mogli opisać for- czymy się prawdopodobnie co najmniej dwudziestu. malną gramatykę i opisać reguły przetwarzania okre- Postarajmy się wobec tego zdefiniować, co w ogóle ślonych struktur. Do tego właśnie służą generatory uważamy za język programowania. -

Compiler Construction
Compiler construction PDF generated using the open source mwlib toolkit. See http://code.pediapress.com/ for more information. PDF generated at: Sat, 10 Dec 2011 02:23:02 UTC Contents Articles Introduction 1 Compiler construction 1 Compiler 2 Interpreter 10 History of compiler writing 14 Lexical analysis 22 Lexical analysis 22 Regular expression 26 Regular expression examples 37 Finite-state machine 41 Preprocessor 51 Syntactic analysis 54 Parsing 54 Lookahead 58 Symbol table 61 Abstract syntax 63 Abstract syntax tree 64 Context-free grammar 65 Terminal and nonterminal symbols 77 Left recursion 79 Backus–Naur Form 83 Extended Backus–Naur Form 86 TBNF 91 Top-down parsing 91 Recursive descent parser 93 Tail recursive parser 98 Parsing expression grammar 100 LL parser 106 LR parser 114 Parsing table 123 Simple LR parser 125 Canonical LR parser 127 GLR parser 129 LALR parser 130 Recursive ascent parser 133 Parser combinator 140 Bottom-up parsing 143 Chomsky normal form 148 CYK algorithm 150 Simple precedence grammar 153 Simple precedence parser 154 Operator-precedence grammar 156 Operator-precedence parser 159 Shunting-yard algorithm 163 Chart parser 173 Earley parser 174 The lexer hack 178 Scannerless parsing 180 Semantic analysis 182 Attribute grammar 182 L-attributed grammar 184 LR-attributed grammar 185 S-attributed grammar 185 ECLR-attributed grammar 186 Intermediate language 186 Control flow graph 188 Basic block 190 Call graph 192 Data-flow analysis 195 Use-define chain 201 Live variable analysis 204 Reaching definition 206 Three address -
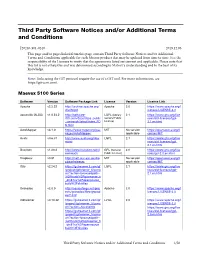
Third Party Software Notices And/Or Additional Terms and Conditions
Third Party Software Notices and/or Additional Terms and Conditions F20240-501-0240 2019.12.06 This page and/or pages linked from this page contain Third Party Software Notices and/or Additional Terms and Conditions applicable for each Matrox product that may be updated from time to time. It is the responsibility of the Licensee to verify that the agreements listed are current and applicable. Please note that this list is not exhaustive and was determined according to Matrox’s understanding and to the best of its knowledge. Note: Links using the GIT protocol require the use of a GIT tool. For more information, see https://git-scm.com/. Maevex 5100 Series Software Version Software Package Link License Version License Link Apache v2.2.22 http://archive.apache.org/ Apache 2.0 https://www.apache.org/l dist/httpd icenses/LICENSE-2.0 asoundlib (ALSA) v1.0.24.2 http://software- LGPL (Library 2.1 https://www.gnu.org/lice dl.ti.com/dsps/dsps_public General Public nses/old-licenses/lgpl- _sw/ezsdk/latest/index_FD License) 2.1.en.html S.html AutoMapper v3.1.0 https://www.nuget.org/pac MIT No version https://opensource.org/li kages/AutoMapper/ applicable censes/MIT Avahi v0.6.31 http://www.avahi.org/dow LGPL 2.1 https://www.gnu.org/lice nload nses/old-licenses/lgpl- 2.1.en.html Busybox v1.20.2 http://www.busybox.net/d GPL (General 2.0 https://www.gnu.org/lice ownloads Public License) nses/gpl-2.0.en.html Dropbear v0.51 http://matt.ucc.asn.au/dro MIT No version https://opensource.org/li pbear/releases applicable censes/MIT Glib v2.24.2 https://gstreamer.ti.com/gf -

1. Why POCS.Key
Symptoms of Complexity Prof. George Candea School of Computer & Communication Sciences Building Bridges A RTlClES A COMPUTER SCIENCE PERSPECTIVE OF BRIDGE DESIGN What kinds of lessonsdoes a classical engineering discipline like bridge design have for an emerging engineering discipline like computer systems Observation design?Case-study editors Alfred Spector and David Gifford consider the • insight and experienceof bridge designer Gerard Fox to find out how strong the parallels are. • bridges are normally on-time, on-budget, and don’t fall ALFRED SPECTORand DAVID GIFFORD • software projects rarely ship on-time, are often over- AS Gerry, let’s begin with an overview of THE DESIGN PROCESS bridges. AS What is the procedure for designing and con- GF In the United States, most highway bridges are budget, and rarely work exactly as specified structing a bridge? mandated by a government agency. The great major- GF It breaks down into three phases: the prelimi- ity are small bridges (with spans of less than 150 nay design phase, the main design phase, and the feet) and are part of the public highway system. construction phase. For larger bridges, several alter- There are fewer large bridges, having spans of 600 native designs are usually considered during the Blueprints for bridges must be approved... feet or more, that carry roads over bodies of water, preliminary design phase, whereas simple calcula- • gorges, or other large obstacles. There are also a tions or experience usually suffices in determining small number of superlarge bridges with spans ap- the appropriate design for small bridges. There are a proaching a mile, like the Verrazzano Narrows lot more factors to take into account with a large Bridge in New Yor:k. -

Writing PHP Extensions
TECHNICAL GUIDE Writing PHP Extensions Introduction Knowing how to use and write PHP extensions is a critical PHP development skill that can save significant time and enable you to quickly add new features to your apps. For example, today, there are more than 150 extensions from the PHP community that provide ready-to-go compiled libraries that enable functions. By using them in your apps, you can avoid developing them yourself. www.zend.com Zend by Perforce © Perforce Software, Inc. All trademarks and registered trademarks are the property of their respective owners. (0320RB20) TECHNICAL GUIDE 2 | Writing PHP Extensions Despite the large number of existing PHP extensions, you may need to write your own. To help you do that, this document describes how to: • Setup a Linux PHP build environment. • Generate an extension skeleton. • Build and install a PHP extension. • Rebuild extensions for production. • Understand extension skeleton file content. • Run extension tests. • Add new functionality (functions, callbacks, constants, global variables, and configuration directives). • Use basic PHP structures, including the API. • Use PHP arrays. • Catch memory leaks. • Manage memory. • Use PHP references. • Use copy on write. • Use PHP classes and objects. • Use object-oriented programming (OOP) in an extension. • Embed C data in PHP objects. • Override object handlers. • Avoid common issues with external library linking, naming conventions, and PHP resource type. To help you learn from all the coding examples in this document, please visit the GIT repository, https://github. com/dstogov/php-extension. It includes a copy of all the files generated when creating the sample extension described in this book. -

Ragel State Machine Compiler User Guide
Ragel State Machine Compiler User Guide by Adrian Thurston License Ragel version 6.1, March 2008 Copyright c 2003-2007 Adrian Thurston This document is part of Ragel, and as such, this document is released under the terms of the GNU General Public License as published by the Free Software Foundation; either version 2 of the License, or (at your option) any later version. Ragel is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PUR- POSE. See the GNU General Public License for more details. You should have received a copy of the GNU General Public License along with Ragel; if not, write to the Free Software Foundation, Inc., 59 Temple Place, Suite 330, Boston, MA 02111-1307 USA i Contents 1 Introduction 1 1.1 Abstract . 1 1.2 Motivation . 1 1.3 Overview . 2 1.4 Related Work . 4 1.5 Development Status . 5 2 Constructing State Machines 6 2.1 Ragel State Machine Specifications . 6 2.1.1 Naming Ragel Blocks . 7 2.1.2 Machine Definition . 7 2.1.3 Machine Instantiation . 7 2.1.4 Including Ragel Code . 7 2.1.5 Importing Definitions . 7 2.2 Lexical Analysis of a Ragel Block . 8 2.3 Basic Machines . 8 2.4 Operator Precedence . 10 2.5 Regular Language Operators . 11 2.5.1 Union . 12 2.5.2 Intersection . 12 2.5.3 Difference . 13 2.5.4 Strong Difference . 13 2.5.5 Concatenation . 14 2.5.6 Kleene Star . -

Apache-Ivy Wordgrinder Nethogs Qtfm Fcgi Enblend-Enfuse
eric Ted fsvs kegs ht tome wmii ttcp ess stgit nut heyu lshw 0th tiger ecl r+e vcp glfw trf sage p6f aris gq dstat vice glpk kvirc scite lyx yagf cim fdm atop slock fann G8$ fmit tkcvs pev bip vym fbida fyre yate yturl ogre owfs aide sdcv ncdu srm ack .eex ddd exim .wm ibam siege eagle xlt xclip gts .pilot atool xskat faust qucs gcal nrpe gavl tintin ruff wdfs spin wink vde+ ldns xpad qxkb kile ent gocr uae rssh gpac p0v qpdf pudb mew cc e afuse igal+ naim lurc xsel fcgi qtfm sphinx vmpk libsmi aterm lxsplit cgit librcd fuseiso squi gnugo spotify verilog kasumi pattern liboop latrace quassel gaupol firehol hydra emoc fi mo brlcad bashdb nginx d en+ xvnkb snappy gemrb bigloo sqlite+ shorten tcludp stardict rss-glx astyle yespl hatari loopy amrwb wally id3tool 3proxy d.ango cvsps cbmfs ledger beaver bsddb3 pptpd comgt x.obs abook gauche lxinput povray peg-e icecat toilet curtain gtypist hping3 clam wmdl splint fribid rope ssmtp grisbi crystal logpp ggobi ccrypt snes>x snack culmus libtirpc loemu herrie iripdb dosbox 8yro0 unhide tclvfs dtach varnish knock tracker kforth gbdfed tvtime netatop 8y,wt blake+ qmmp cgoban nexui kdesvn xrestop ifstatus xforms gtklife gmrun pwgen httrack prelink trrnt ip qlipper audiere ssdeep biew waon catdoc icecast uif+iso mirage epdfview tools meld subtle parcellite fusesmb gp+fasta alsa-tools pekwm viewnior mailman memuse hylafax= pydblite sloccount cdwrite uemacs hddtemp wxGT) adom .ulius qrencode usbmon openscap irssi!otr rss-guard psftools anacron mongodb nero-aac gem+tg gambas3 rsnapshot file-roller schedtool