Who Gains and Who Loses in Derivatives Trading, and Why? Evidence from Chinese Brokerage Account Data∗
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The History of Gyalthang Under Chinese Rule: Memory, Identity, and Contested Control in a Tibetan Region of Northwest Yunnan
THE HISTORY OF GYALTHANG UNDER CHINESE RULE: MEMORY, IDENTITY, AND CONTESTED CONTROL IN A TIBETAN REGION OF NORTHWEST YUNNAN Dá!a Pejchar Mortensen A dissertation submitted to the faculty at the University of North Carolina at Chapel Hill in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the Department of History. Chapel Hill 2016 Approved by: Michael Tsin Michelle T. King Ralph A. Litzinger W. Miles Fletcher Donald M. Reid © 2016 Dá!a Pejchar Mortensen ALL RIGHTS RESERVED ii! ! ABSTRACT Dá!a Pejchar Mortensen: The History of Gyalthang Under Chinese Rule: Memory, Identity, and Contested Control in a Tibetan Region of Northwest Yunnan (Under the direction of Michael Tsin) This dissertation analyzes how the Chinese Communist Party attempted to politically, economically, and culturally integrate Gyalthang (Zhongdian/Shangri-la), a predominately ethnically Tibetan county in Yunnan Province, into the People’s Republic of China. Drawing from county and prefectural gazetteers, unpublished Party histories of the area, and interviews conducted with Gyalthang residents, this study argues that Tibetans participated in Communist Party campaigns in Gyalthang in the 1950s and 1960s for a variety of ideological, social, and personal reasons. The ways that Tibetans responded to revolutionary activists’ calls for political action shed light on the difficult decisions they made under particularly complex and coercive conditions. Political calculations, revolutionary ideology, youthful enthusiasm, fear, and mob mentality all played roles in motivating Tibetan participants in Mao-era campaigns. The diversity of these Tibetan experiences and the extent of local involvement in state-sponsored attacks on religious leaders and institutions in Gyalthang during the Cultural Revolution have been largely left out of the historiographical record. -

UC GAIA Chen Schaberg CS5.5-Text.Indd
Idle Talk New PersPectives oN chiNese culture aNd society A series sponsored by the American Council of Learned Societies and made possible through a grant from the Chiang Ching-kuo Foundation for International Scholarly Exchange 1. Joan Judge and Hu Ying, eds., Beyond Exemplar Tales: Women’s Biography in Chinese History 2. David A. Palmer and Xun Liu, eds., Daoism in the Twentieth Century: Between Eternity and Modernity 3. Joshua A. Fogel, ed., The Role of Japan in Modern Chinese Art 4. Thomas S. Mullaney, James Leibold, Stéphane Gros, and Eric Vanden Bussche, eds., Critical Han Studies: The History, Representation, and Identity of China’s Majority 5. Jack W. Chen and David Schaberg, eds., Idle Talk: Gossip and Anecdote in Traditional China Idle Talk Gossip and Anecdote in Traditional China edited by Jack w. cheN aNd david schaberg Global, Area, and International Archive University of California Press berkeley los Angeles loNdoN The Global, Area, and International Archive (GAIA) is an initiative of the Institute of International Studies, University of California, Berkeley, in partnership with the University of California Press, the California Digital Library, and international research programs across the University of California system. University of California Press, one of the most distinguished university presses in the United States, enriches lives around the world by advancing scholarship in the humanities, social sciences, and natural sciences. Its activities are supported by the UC Press Foundation and by philanthropic contributions from individuals and institutions. For more information, visit www.ucpress.edu. University of California Press Berkeley and Los Angeles, California University of California Press, Ltd. -

Chronology of Chinese History
AppendixA 1257 Appendix A Chronology of Chinese History Xla Dynasty c. 2205 - c. 1766 B. C. Shang Dynasty c. 1766 - c. 1122 B. C. Zhou Dynasty c. 1122 - 249 B. C. Western Zhou c. 1122 - 771 B.C. Eastern Zhou 770 - 249 B. C. Spring Autumn and period 770 - 481 B.C. Warring States period 403 - 221 B.C. Qin Dynasty 221 - 207 B. C. Han Dynasty 202 B. C. - A. D. 220 Western Han 202 B.C. -AD. 9 Xin Dynasty A. D. 9-23 Eastern Han AD. 25 - 220 Three Kingdoms 220 - 280 Wei 220 - 265 Shu 221-265 Wu 222 - 280 Jin Dynasty 265 - 420 Western Jin 265 - 317 Eastern Jin 317 - 420 Southern and Northern Dynasties 420 - 589 Sui Dynasty 590 - 618 Tang Dynasty 618 - 906 Five Dynasties 907 - 960 Later Liang 907 - 923 Later Tang 923 - 936 Later Jin 936 - 947 Later Han 947 - 950 Later Zhou 951-960 Song Dynasty 960-1279 Northern Song 960-1126 Southern Song 1127-1279 Liao 970-1125 Western Xia 990-1227 Jin 1115-1234 Yuan Dynasty 1260-1368 Ming Dynasty 1368-1644 Cling Dynasty 1644-1911 Republic 1912-1949 People's Republic 1949- 1258 Appendix B Map of China C ot C x VV 00 aý 3 ýý, cý ýý=ý<<ý IAJ wcsNYý..®c ýC9 0 I Jz ýS txS yQ XZL ý'Tl '--} -E 0 JVvýc ý= ' S .. NrYäs Zw3!v )along R ?yJ L ` (Yana- 'ý. ý. wzX: 0. ý, {d Q Z lýý'? ý3-ýý`. e::. ý z 4: `ý" ý i kws ". 'a$`: ýltiCi, Ys'ýlt.^laS-' tý.. -

恒投證券 Hengtou Securities
Hong Kong Exchanges and Clearing Limited and The Stock Exchange of Hong Kong Limited take no responsibility for the contents of this announcement, make no representation as to its accuracy or completeness and expressly disclaim any liability whatsoever for any loss howsoever arising from or in reliance upon the whole or any part of the contents of this announcement. 恒投證券 HENGTOU SECURITIES (a joint stock company incorporated in the People’s Republic of China with limited liability under the Chinese corporate name “恒泰證券股份有限公司” and carrying on business in Hong Kong as “恒投證券” (in Chinese) and “HENGTOU SECURITIES” (in English)) (the “Company”) (Stock code: 01476) ANNUAL RESULTS ANNOUNCEMENT FOR THE YEAR ENDED 31 DECEMBER 2016 The board of directors (the “Board”) of the Company hereby announces the audited annual results of the Company and its subsidiaries for the year ended 31 December 2016. This announcement, containing the full text of the 2016 annual report of the Company, complies with the relevant requirements of the Rules Governing the Listing of Securities on The Stock Exchange of Hong Kong Limited in relation to information to accompany preliminary announcement of annual results and has been reviewed by the audit committee of the Company. The Board resolved that no profit distribution will be made for the year ended 31 December 2016. PUBLICATION OF ANNUAL RESULTS ANNOUNCEMENT AND ANNUAL REPORT This annual results announcement will be published on the websites of The Stock Exchange of Hong Kong Limited (www.hkexnews.hk) and the Company (www.cnht.com.cn). The 2016 annual report of the Company will be dispatched to the shareholders of the Company and published on the websites of The Stock Exchange of Hong Kong Limited and the Company in due course but no later than the end of April 2017. -
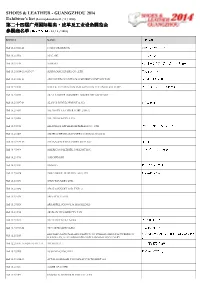
SLG14 Exhibitors List 23 May 2014 (Website).Xlsx
SHOES & LEATHER - GUANGZHOU 2014 Exhibitor's list (Last updated on 23 / 5 / 2014) 第二十四届广州州国际国际鞋鞋类类类、、、皮革及工皮革及工业设备展展览会览会 参参展商名展商名单 (最后更新日期: 23 / 5 / 2014) BOOTH NAME 公司名称称称 Hall 11.2/0521-22 169 INFORMATION 169 资讯《鞋业&皮革信息》 Hall 10.2/0703 A.P.C. SRL 阿皮奇有限公司 Hall 10.2/0719 A.SHOES 東莞市華瑞世界鞋業總部基地有限公司 Hall 11.2/0114-16, 0135-37 ADINA MACHINERY CO., LTD. 艾特拿有限公司 Hall 11.2/0426-28 ADVANCED OCTOPUS MACHINERY COMPANY LTD 洋逸机械发展有限公司 Hall 11.2/0833 AITECK AUTOMATION INTEGRATION TECHNOLOGY CORP. 鸿宇自动化设备股份有限公司 Hall 10.2/0319 AKA LEATHER INDUSTRY AND TRADE COMPANY Hall 10.2/0537-38 ALAN\'S DEVELOPMENT & CO. 锦华发展公司 Hall 10.2/0313 ALL RIGHT LEATHER CORP. (ARLC) Hall 11.2/0205 ALL TRENDS PTE. LTD. Hall 11.2/0733 ALLFINELY APPLIED MATERIALS CO., LTD. 欧桦应用材料股份有限公司 Hall 11.2/0307 ALLIED CHEMICALS INTERNATIONAL CO.,LTD. Hall 11.2/0435-36 AMANN & SOEHNE GMBH & CO. KG 亚曼集团 Hall 10.2/0428 AMERICAN BILTRITE FAR EAST INC. 美國普得利上海代表處 Hall 10.2/0733 AMICHEM SRL Hall 12.2/0421 ANWOO 广州安予贸易有限公司 Hall 11.2/0324 AOKAI SHOE MATERIAL CO.,LTD 奥凯鞋材有限公司 Hall 10.2/0331 APEX TANNERY LTD. Hall 10.2/0332 APEX TANNERY LTD. UNIT-2 Hall 12.2/0335 ARES ITALIA S.R.L. Hall 11.2/0528 ARS ARPEL SCHOOL & MAGAZINES Hall 10.2/0715 ARTISAN LEATHER PVT LTD Hall 11.2/0622 ASIA FOOTWERA NEWS 《亚洲鞋业》杂志 Hall 10.2/0203-04 ASIA STAR CHINA LTD. 立辉中国有限公司 ASSOMAC-NATIONAL ASSOCIATION OF ITALIAN MANUFACTURERS OF 阿索玛科- 意大利制鞋,制革, 制皮具机械协 Hall 12.2/0215 FOOTWEAR, LEATHERGOODS AND TANNING MACHINERY 会 Hall 12.2/0111-15, 0230-34, 0311-14 ATOM S.P.A. -

Comparison of the Grain Quality and Starch Physicochemical Properties
agriculture Article Comparison of the Grain Quality and Starch Physicochemical Properties between Japonica Rice Cultivars with Different Contents of Amylose, as Affected by Nitrogen Fertilization Yajie Hu , Shumin Cong and Hongcheng Zhang * Jiangsu Co-Innovation Center for Modern Production Technology of Grain Crops, Jiangsu Key Laboratory of Crop Genetics and Physiology, Yangzhou University, Yangzhou 225009, China; [email protected] (Y.H.); [email protected] (S.C.) * Correspondence: [email protected] Abstract: In order to determine the effects of nitrogen fertilizer on the grain quality and starch physic- ochemical properties of japonica rice cultivars with different contents of amylose, normal amylose content (NAC) and low amylose content (LAC) cultivars were grown in a field, with or without nitrogen fertilizer (WN). The relationships between the amylose content, starch physicochemical properties and eating quality were also examined. Compared with WN, nitrogen fertilizer (NF) significantly increased the grain yield but markedly decreased the grain weight. In addition, the processing quality tended to improve, but the appearance quality and eating quality deteriorated under NF application. The grain yield was similar between NAC and LAC cultivars. However, the grain quality and starch physicochemical properties were significantly different between NAC and LAC cultivars. The palatability of the cooked rice was significantly higher in the LAC than in NAC Citation: Hu, Y.; Cong, S.; Zhang, H. cultivar, which was due to its lower amylose content, protein content, hardness, and retrogradation Comparison of the Grain Quality and enthalpy and degree, and its higher stickiness, peak viscosity, breakdown, relative crystallinity and Starch Physicochemical Properties peak intensity. The amylose content and protein content were significantly negatively correlated with between Japonica Rice Cultivars with Different Contents of Amylose, as the palatability. -

Annual Report 2015
(於中華人民共和國以中文公司名稱「恒泰證券股份 (a joint stock company incorporated in the People’s 有限公司」註冊成立的股份有限公司,在香港以 Republic of China with limited liability under the Chinese corporate name “恒泰證券股份有限公司” and 「恒投證券」(中文)及「HENGTOU SECURITIES」 carrying on business in Hong Kong as “恒投證券” (in (英文)名義開展業務) Chinese) and “HENGTOU SECURITIES” (in English)) 股份代碼:1476 Stock Code: 1476 2015 2015 年度報告 Annual Report 2015 Annual ReportAnnual 年度報告 CONTENTS Important Notice 2 Chairman’s Statement 3 Section 1 Definitions 4 Section 2 Material Risks 9 Section 3 Company Profile 10 Section 4 Summary of Accounting and Business Data 22 Section 5 Management Discussion and Analysis 27 Section 6 Report of the Board of Directors 76 Section 7 Other Material Particulars 86 Section 8 Equity (Capital) Changes and Substantial Shareholders 93 Section 9 Directors, Supervisors, Senior Management and Employees 98 Section 10 Corporate Governance Report 115 Appendix Particulars of Securities Branches 142 Independent Auditor’s Report 155 Consolidated Statement of Profit or Loss and Other Comprehensive Income 157 Consolidated Statement of Financial Position 159 Consolidated Statement of Changes in Equity 162 Consolidated Cash Flow Statement 164 Notes to the Financial Statements 167 Important Notice The Board, Supervisory Committee, Directors, Supervisors and senior management of the Company undertake that the content of the annual report is true, accurate, complete and without any false record, misrepresentation or material omission and are severally and jointly liable therefor. This report has been considered and approved at the fourth meeting of the third session of the Board and the third meeting of the third session of Supervisory Committee where eight Directors and all Supervisors were present, respectively. -

恒投證券 Hengtou Securities
Hong Kong Exchanges and Clearing Limited and The Stock Exchange of Hong Kong Limited take no responsibility for the contents of this announcement, make no representation as to its accuracy or completeness and expressly disclaim any liability whatsoever for any loss howsoever arising from or in reliance upon the whole or any part of the contents of this announcement. 恒投證券 HENGTOU SECURITIES (A joint stock company incorporated in the People’s Republic of China with limited liability under the Chinese corporate name “ 恒 泰 證 券股份有限公司 ” and carrying on business in Hong Kong as “ 恒投證券 ” (in Chinese) and “HENGTOU SECURITIES” (in English)) (the “Company”) (Stock Code: 01476) ANNUAL RESULTS ANNOUNCEMENT FOR THE YEAR ENDED 31 DECEMBER 2017 The board of directors (the “Board”) of the Company hereby announces the audited annual results of the Company and its subsidiaries for the year ended 31 December 2017. This announcement, containing the full text of the 2017 annual report of the Company, complies with the relevant requirements of the Rules Governing the Listing of Securities on The Stock Exchange of Hong Kong Limited in relation to information to accompany preliminary announcement of annual results and has been reviewed by the audit committee of the Company. PUBLICATION OF ANNUAL RESULTS ANNOUNCEMENT AND ANNUAL REPORT This annual results announcement will be published on the websites of The Stock Exchange of Hong Kong Limited (www.hkexnews.hk) and the Company (www.cnht.com.cn). The 2017 annual report of the Company will be dispatched to the shareholders of the Company and published on the websites of The Stock Exchange of Hong Kong Limited and the Company in due course but no later than the end of April 2018. -

(Main Products) Electrical Equipments Chongqing Yuneng
Post Name of enterprise Industry Address Tel. Web Main business (main products) code Electrical equipments Aluminum stranded conductor steel-reinforced Chongqing Yuneng Manufacture No.1, Jinguo Avenue, National http://www.cqtaishan.co wire up to 1000kV, power cable up to 500kV, Taishan Electric of electric Agricultural Technology Park, 401120 023-61898188 m/ magnetic conductor, cable used for electric Wire&Cable Co., Ltd. wire & cable Yubei Dist., Chongqing equipment, special cable and so on Manufacture of ABB Chongqing No. 1, Huayannan Village, EHV transformers and reactors of 500kV and transformers, 400052 023 69093688 http://www.abb.com.cn/ Transformer Co., Ltd. Jiulongpo Dist., Chongqing above rectifiers & inductors Switch disconnectors with capacity up to 220kV, 110kV, SF6 gas insulated switchgear Manufacture (GIS)and self-interrupter SF6 circuit of breaker, 10~220kV Oil power transformer Chongqing AEA Electric distribution No.38, Jingjiqiao, Shapingba http://www.cqaea.com 400051 023-61717786 and CT&PT, 0.6~35kV resin cast power (group) Co., Ltd. switches & Dist., Chongqing / transformer and CT&PT, complete sets of control switch devices up to 35kV, prefabricated equipments substations, integrated power automation system and so on Manufacture Chongqing Electric of Yuqingsi, Zhongliangshan, http://www.cemf.com. AC&DC motors, small and medium-sized 400052 023-89093000 Machine Federation Ltd. electromotor Chongqing cn/ generators, turbines and so on s Wire, cable, anaerobic copper bar, electric Chongqing Pigeon Manufacture No. 998, Konggang http://www.cq-cable.co copper wire, copper profile, copper and Electric Wire&Cable Co., of electric 401120 023-67166111 Avenue,Yubei Dist., Chongqing m/ copper alloy rod, HV&LV electric porcelain Ltd. -
C M Y Cm My Cy My K
2098_CapaCatálogo_Hospitalar_155x230_v7_AF.pdf 1 5/4/17 12:00 PM C M Y CM MY CY CMY K Todas as informações contidas neste Catálogo estão disponíveis no site hospitalar.com em 3 idiomas. Índice Informações Gerais ......................................................................................04 Mensagem HOSPITALAR ..............................................................................08 Mensagem CNS ...........................................................................................10 Mensagem FENAESS ....................................................................................11 Mensagem SINDHOSP .................................................................................12 Mensagem ANAHP ......................................................................................13 Mensagem ABIMO ......................................................................................14 Perfil dos Expositores ..................................................................................16 Expositores por Segmento ........................................................................352 Lista de Expositores ...................................................................................373 Este catálogo contém as relações dos expositores que informaram seus dados até 20/04/2017. As empresas aparecem por ordem alfabética , com sua localização na feira, endereço, produtos e marca. All information contained in this Catalogue is available on the website hospitalar.com in 3 languages. Index General Information -
Winners, Losers, and Regulators in a Nascent Derivatives Market: Evidence from Chinese Brokerage Data∗
Winners, Losers, and Regulators in a Nascent Derivatives Market: Evidence from Chinese Brokerage Data∗ Xindan Li,† Avanidhar Subrahmanyam,‡ and Xuewei Yang§ May 7, 2018 ∗We are grateful to the anonymous brokerage firm for providing the data used in this study, and to Ning Xu for helpful discussions about the institutional details of the Chinese warrant market. We thank Bruce Carlin, Mikhail Chernov, Haoyu Gao, Mark Grinblatt, Valentin Haddad, Kabir Hassan, Sudha Krishnaswami, Nan Li, Zhongfei Li, Yanchu Liu, William Mann, Tyler Muir, Tarun Mukherjee, Atsuyuki Naka, Deng Pan, Pei Pei, Tao Shen, Haibing Shu, Lijian Wei, Zhishu Yang, Jiaquan Yao, Lihong Zhang, Rui Zhong, Shushang Zhu, and participants in seminars at UCLA, the University of New Orleans, Sun Yat-Sen University, Shanghai Jiao Tong University, Tsinghua University, Xiamen University, and Central University of Finance and Economics (Beijing), for helpful comments and suggestion- s. We also appreciate Dan Tang and Dazhou Wang for their help with the data. Xindan Li acknowledges support by National Natural Science Foundation of China (No. 71720107001). Xuewei Yang acknowledges support by National Natural Science Foundation of China (No. 71771115). All errors are solely the authors’ responsibility. †School of Management and Engineering, Nanjing University, 22 Hankou Road, Nanjing, Jiangsu 210093, China. ‡Anderson Graduate School of Management, University of California at Los Angeles, Los Angeles, CA 90095, USA. Phone: +1 310 825-5355; email: [email protected] §School of Management and Engineering, Nanjing University, 22 Hankou Road, Gulou District, Nanjing, Jiangsu 210093, China. Email: [email protected], [email protected] Winners, Losers, and Regulators in a Nascent Derivatives Market: Evidence from Chinese Brokerage Data May 7, 2018 Abstract In contrast to a wealth of knowledge on trading in equity markets, comparatively little is known about who gains and who underperforms in derivatives trading. -

C OATINGS Show 2017 Adhesives – Sealants – Construction Chemicals
EUROPeaN C OATINGS SHOW 2017 ADHesIVes – SealaNTS – CONSTRUCTION CHEMIcals NUREMBERG // GERMANY European Coatings Show: 4 –6 April 2017 European Coatings Show Conference: 3 –4 April 2017 LIST OF EXHIBITORS www.european-coatings-show.com AIR PRODUCTS & CHEMICAL 4 - 4-340 2 Utrecht, Netherlands 20 Microns Ltd. 7 - 7-756 AKS Coatings GmbH 4A - 4A-406i Vadodara, India Altlußheim, Germany Akzo Nobel Chemicals AG 1 - 1-444 A Sempach Station, Switzerland A C R S.r.l. 5 - 5-323 AkzoNobel 1 - 1-444 Parma, Italy Stenungsund, Sweden Aako BV 7 - 7-334 AkzoNobel 1 - 1-444 Leusden, Netherlands , Sweden abcr GmbH 4 - 4-110 AkzoNobel PPC 1 - 1-444 Karlsruhe, Germany Bohus, Sweden ABRAFATI 7A - 7A-713 AkzoNobel Surface Chemistry AB 1 - 1-444 Sao Paulo SP, Brazil Stenungsund, Sweden ACC BEKU - Herstellung u. Vertrieb 4A - 4A-519 AL-FARBEN (TORRECID GROUP) 7A - 7A-111 chemischer Spezialerzeugnisse GmbH Alcora (Castellón), Spain Edenkoben, Germany ALBA ALUMINIU Srl 4A - 4A-209 Accoat A/S 5 - 5-116 Zlatna, Romania Kvistgaard, Denmark Albemarle Europe sprl 4 - 4-640 Aceto Corporation 4 - 4-512 Louvain-la-Neuve, Belgium Hamburg, Germany Alberdingk Boley GmbH 7 - 7-556 Achitex Minerva S.p.A. 4 - 4-611 Krefeld, Germany Vaiano Cremasco, Italy Alfa S.r.l. 5 - 5-428 ACME Tech.Co.,Ltd 7 - 7-452 Bologna, Italy Chongqing, China Alfa S.r.l. 5 - 5-426 ACT Test Panels LLC 5 - 5-135 Bologna, Italy Hillsdale, United States Alfred Kochen GmbH & Co.KG 7 - 7-526 Active Minerals International 7A - 7A-304 Hamburg, Germany Sparks, United States Alichem P.