Go Game Formal Revealing by Ising Model
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Booxter Export Page 1
Cover Title Authors Edition Volume Genre Format ISBN Keywords The Museum of Found Mirjam, LINSCHOOTEN Exhibition Soft cover 9780968546819 Objects: Toronto (ed.), Sameer, FAROOQ Catalogue (Maharaja and - ) (ed.), Haema, SIVANESAN (Da bao)(Takeout) Anik, GLAUDE (ed.), Meg, Exhibition Soft cover 9780973589689 Chinese, TAYLOR (ed.), Ruth, Catalogue Canadian art, GASKILL (ed.), Jing Yuan, multimedia, 21st HUANG (trans.), Xiao, century, Ontario, OUYANG (trans.), Mark, Markham TIMMINGS Piercing Brightness Shezad, DAWOOD. (ill.), Exhibition Hard 9783863351465 film Gerrie, van NOORD. (ed.), Catalogue cover Malenie, POCOCK (ed.), Abake 52nd International Art Ming-Liang, TSAI (ill.), Exhibition Soft cover film, mixed Exhibition - La Biennale Huang-Chen, TANG (ill.), Catalogue media, print, di Venezia - Atopia Kuo Min, LEE (ill.), Shih performance art Chieh, HUANG (ill.), VIVA (ill.), Hongjohn, LIN (ed.) Passage Osvaldo, YERO (ill.), Exhibition Soft cover 9780978241995 Sculpture, mixed Charo, NEVILLE (ed.), Catalogue media, ceramic, Scott, WATSON (ed.) Installaion China International Arata, ISOZAKI (ill.), Exhibition Soft cover architecture, Practical Exhibition of Jiakun, LIU (ill.), Jiang, XU Catalogue design, China Architecture (ill.), Xiaoshan, LI (ill.), Steven, HOLL (ill.), Kai, ZHOU (ill.), Mathias, KLOTZ (ill.), Qingyun, MA (ill.), Hrvoje, NJIRIC (ill.), Kazuyo, SEJIMA (ill.), Ryue, NISHIZAWA (ill.), David, ADJAYE (ill.), Ettore, SOTTSASS (ill.), Lei, ZHANG (ill.), Luis M. MANSILLA (ill.), Sean, GODSELL (ill.), Gabor, BACHMAN (ill.), Yung -

Weiqi in Australia
Weiqi in Australia Neville Smythe, Australian Go Association australiango.asn.au Weiqi in Australia • Earliest game played in Australia? • 1960 – Go played at Sydney Chess Club • by 1970, Sydney Go Club formed • 1972 Canberra club • 1977 Brisbane club • 1980 Melbourne club An early Sydney player… John Power (right) with Richard Bozulich and friend (WAGC 2008) Weiqi in Australia • 1978 – Sydney Brisbane and Canberra Clubs meet to form Australian Go Association • 1978 –1st National Championship • 1979 – played in first WAGC • 1982 – foundation member IGF • National, State and other tournaments since then Tournaments National Championship 2007 (Sydney Go Club) Tournaments NEC Cup 2009 Australian Go Congress 2nd Australian Go Congress 2016 [4 colour Go – madness!] World Collegiate Championship Sydney University, July 2019 International participation 1st WAGC 1979: Dae Hahn (Australia) v Shin-Auk Kang (USA) International participation Team Australia WMSG Beijing 2008 (we claim JiaJia as Australian!) 2019 status • Over 500 members, 15 clubs • Strong participation and support by the expatriate Chinese and Korean communities • Not enough female players The future Internet – blessing or curse? • Beginners now progress very quickly and can play anyone anywhere any time • But • We have no idea how many people in Australia only play on-line • Viability of physical clubs is under threat • But it can be an opportunity… Internet – blessing or curse? http://club.artofgo.org/ National Treasures Wu Soong Shen at 2004 Australian National Championship Canberra National Treasures An Younggil, National Coach Visiting Professionals Kobayashi Chizu meeting emus (Canberra, 1981) Visiting Professionals • Chizu was one of the first pro’s to visit • (Before Chizu 3 players from the Nihon Kiin in 1975) • Since then many professionals from Japan, Korea and China have visited • .. -

Challenge Match Game 5: “Renewal”
Challenge Match 8-15 March 2016 Game 5: “Renewal” Commentary by Fan Hui Go expert analysis by Gu Li and Zhou Ruiyang Translated by Lucas Baker, Thomas Hubert, and Thore Graepel Renewal Lee Sedol’s triumph in the fourth game attracted a surge of interest in the match throughout the world. Even the Western media, including CNN and the BBC, came to conduct reports and interviews. For Go, this level of attention was utterly unprecedented. More and more people started trying to learn and understand the game. To give just one example, Go Game Guru, the largest Go website in English, reported that its daily visitors had jumped tenfold. In Korea, the heart of the craze, the media could talk of little else. For the next two days, the top three items at every news station invariably had something to do with the match. After winning the fourth game, Lee Sedol had risen to the status of a national hero. His brave request during the press conference after the fourth game was particularly inspiring. Normally, the two players would have chosen colors in the fifth game by nigiri, but Lee asked to play Black. The reason was simple: although AlphaGo prefers White, Lee had won as White already, and wanted to prove he was equally capable of winning with Black. His courageous spirit deeply moved the team, so for the fifth game, there was no need to choose colors. Lee would take Black. After the fourth game, people had finally seen that AlphaGo was not invincible. Though the outcome of the match had already been decided, the result of the fifth game now seemed more important than the winner of the contest. -

Sydney Go Journal Issue Date – February 2007
Author – David Mitchell on behalf of The Sydney Go Club Sydney Go Journal Issue Date – February 2007 Dr. Geoffrey Gray’s antique Go Ban (picture courtesy of Dr Gray) Up coming events Queensland Go Championship Saturday 17th and Sunday 18th February in Brisbane. Venue: Brisbane Bridge Centre Registration and other details on page 33 For the latest details visit www.uq.net.au/~zzjhardy/brisgo.html Contributions, comments and suggestions for the SGJ to: [email protected] Special thanks to Devon Bailey and Geoffrey Gray for proof reading this edition and correcting my mistakes. © Copyright 2007 – David Mitchell Page 1 February 2007 Author – David Mitchell on behalf of The Sydney Go Club Sydney Lightning Tournament report 3 Changqi Cup 4 3rd Changqi Cup – 1st Qualifier 6 3rd Changqi Cup – 2nd Qualifier 10 Problems 14 Handicap Strategy 15 Four Corners 29 Two page Joseki lesson 35 Answers 37 Korean Go Terms 39 The Sydney Go Club Meets Friday nights at :- At Philas House 17 Brisbane St Surry Hills From 5.00pm Entrance fee - $5 per head; Concession $3; Children free - includes tea and coffee. For further information from Robert [email protected] © Copyright 2007 – David Mitchell Page 2 February 2007 Lightning Tournament The lightning tournament was held on the January 12th and a good time was had by all, thanks to Robert Vadas organising skills. The final was between Max Latey and David Mitchell, the latter managing another lucky win. The following pictures tell the story David Mitchell (foreground); Max more eloquently than words. Latey (background); the two finalists Robert giving some sage advice. -
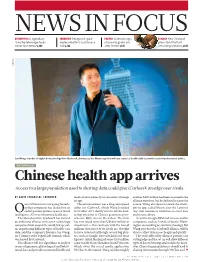
Chinese Health App Arrives Access to a Large Population Used to Sharing Data Could Give Icarbonx an Edge Over Rivals
NEWS IN FOCUS ASTROPHYSICS Legendary CHEMISTRY Deceptive spice POLITICS Scientists spy ECOLOGY New Zealand Arecibo telescope faces molecule offers cautionary chance to green UK plans to kill off all uncertain future p.143 tale p.144 after Brexit p.145 invasive predators p.148 ICARBONX Jun Wang, founder of digital biotechnology firm iCarbonX, showcases the Meum app that will use reams of health data to provide customized medical advice. BIOTECHNOLOGY Chinese health app arrives Access to a large population used to sharing data could give iCarbonX an edge over rivals. BY DAVID CYRANOSKI, SHENZHEN medical advice directly to consumers through another $400 million had been invested in the an app. alliance members, but he declined to name the ne of China’s most intriguing biotech- The announcement was a long-anticipated source. Wang also demonstrated the smart- nology companies has fleshed out an debut for iCarbonX, which Wang founded phone app, called Meum after the Latin for earlier quixotic promise to use artificial in October 2015 shortly after he left his lead- ‘my’, that customers would use to enter data Ointelligence (AI) to revolutionize health care. ership position at China’s genomics pow- and receive advice. The Shenzhen firm iCarbonX has formed erhouse, BGI, also in Shenzhen. The firm As well as Google, IBM and various smaller an ambitious alliance with seven technology has now raised more than US$600 million in companies, such as Arivale of Seattle, Wash- companies from around the world that special- investment — this contrasts with the tens of ington, are working on similar technology. But ize in gathering different types of health-care millions that most of its rivals are thought Wang says that the iCarbonX alliance will be data, said the company’s founder, Jun Wang, to have invested (although several big play- able to collect data more cheaply and quickly. -

CSC321 Lecture 23: Go
CSC321 Lecture 23: Go Roger Grosse Roger Grosse CSC321 Lecture 23: Go 1 / 22 Final Exam Monday, April 24, 7-10pm A-O: NR 25 P-Z: ZZ VLAD Covers all lectures, tutorials, homeworks, and programming assignments 1/3 from the first half, 2/3 from the second half If there's a question on this lecture, it will be easy Emphasis on concepts covered in multiple of the above Similar in format and difficulty to the midterm, but about 3x longer Practice exams will be posted Roger Grosse CSC321 Lecture 23: Go 2 / 22 Overview Most of the problem domains we've discussed so far were natural application areas for deep learning (e.g. vision, language) We know they can be done on a neural architecture (i.e. the human brain) The predictions are inherently ambiguous, so we need to find statistical structure Board games are a classic AI domain which relied heavily on sophisticated search techniques with a little bit of machine learning Full observations, deterministic environment | why would we need uncertainty? This lecture is about AlphaGo, DeepMind's Go playing system which took the world by storm in 2016 by defeating the human Go champion Lee Sedol Roger Grosse CSC321 Lecture 23: Go 3 / 22 Overview Some milestones in computer game playing: 1949 | Claude Shannon proposes the idea of game tree search, explaining how games could be solved algorithmically in principle 1951 | Alan Turing writes a chess program that he executes by hand 1956 | Arthur Samuel writes a program that plays checkers better than he does 1968 | An algorithm defeats human novices at Go 1992 -

Residual Networks for Computer Go Tristan Cazenave
Residual Networks for Computer Go Tristan Cazenave To cite this version: Tristan Cazenave. Residual Networks for Computer Go. IEEE Transactions on Games, Institute of Electrical and Electronics Engineers, 2018, 10 (1), 10.1109/TCIAIG.2017.2681042. hal-02098330 HAL Id: hal-02098330 https://hal.archives-ouvertes.fr/hal-02098330 Submitted on 12 Apr 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. IEEE TCIAIG 1 Residual Networks for Computer Go Tristan Cazenave Universite´ Paris-Dauphine, PSL Research University, CNRS, LAMSADE, 75016 PARIS, FRANCE Deep Learning for the game of Go recently had a tremendous success with the victory of AlphaGo against Lee Sedol in March 2016. We propose to use residual networks so as to improve the training of a policy network for computer Go. Training is faster than with usual convolutional networks and residual networks achieve high accuracy on our test set and a 4 dan level. Index Terms—Deep Learning, Computer Go, Residual Networks. I. INTRODUCTION Input EEP Learning for the game of Go with convolutional D neural networks has been addressed by Clark and Storkey [1]. It has been further improved by using larger networks [2]. -

E-Book? Začala Hra
Nejlepší strategie všech dob 1 www.yohama.cz Nejlepší strategie všech dob Obsah OBSAH DESKOVÁ HRA GO ................................................................................................................................ 3 Úvod ............................................................................................................................................................ 3 Co je to go ................................................................................................................................................... 4 Proč hrát go ................................................................................................................................................. 7 Kde získat go ................................................................................................................................................ 9 Jak začít hrát go ......................................................................................................................................... 10 Kde a s kým hrát go ................................................................................................................................... 12 Jak se zlepšit v go ...................................................................................................................................... 14 Handicapová hra ....................................................................................................................................... 15 Výkonnostní třídy v go a rating hráčů ....................................................................................................... -

FUEGO—An Open-Source Framework for Board Games and Go Engine Based on Monte Carlo Tree Search Markus Enzenberger, Martin Müller, Broderick Arneson, and Richard Segal
IEEE TRANSACTIONS ON COMPUTATIONAL INTELLIGENCE AND AI IN GAMES, VOL. 2, NO. 4, DECEMBER 2010 259 FUEGO—An Open-Source Framework for Board Games and Go Engine Based on Monte Carlo Tree Search Markus Enzenberger, Martin Müller, Broderick Arneson, and Richard Segal Abstract—FUEGO is both an open-source software framework with new algorithms that would not be possible otherwise be- and a state-of-the-art program that plays the game of Go. The cause of the cost of implementing a complete state-of-the-art framework supports developing game engines for full-information system. Successful previous examples show the importance of two-player board games, and is used successfully in a substantial open-source software: GNU GO [19] provided the first open- number of projects. The FUEGO Go program became the first program to win a game against a top professional player in 9 9 source Go program with a strength approaching that of the best Go. It has won a number of strong tournaments against other classical programs. It has had a huge impact, attracting dozens programs, and is competitive for 19 19 as well. This paper gives of researchers and hundreds of hobbyists. In Chess, programs an overview of the development and current state of the UEGO F such as GNU CHESS,CRAFTY, and FRUIT have popularized in- project. It describes the reusable components of the software framework and specific algorithms used in the Go engine. novative ideas and provided reference implementations. To give one more example, in the field of domain-independent planning, Index Terms—Computer game playing, Computer Go, FUEGO, systems with publicly available source code such as Hoffmann’s man-machine matches, Monte Carlo tree search, open source soft- ware, software frameworks. -

Achieving Master Level Play in 9X9 Computer Go
Proceedings of the Twenty-Third AAAI Conference on Artificial Intelligence (2008) Achieving Master Level Play in 9 9 Computer Go × Sylvain Gelly∗ David Silver† Univ. Paris Sud, LRI, CNRS, INRIA, France University of Alberta, Edmonton, Alberta, Canada Abstract simulated, using self-play, starting from the current position. Each position in the search tree is evaluated by the average The UCT algorithm uses Monte-Carlo simulation to estimate outcome of all simulated games that pass through that po- the value of states in a search tree from the current state. However, the first time a state is encountered, UCT has no sition. The search tree is used to guide simulations along knowledge, and is unable to generalise from previous expe- promising paths. This results in a highly selective search rience. We describe two extensions that address these weak- that is grounded in simulated experience, rather than an ex- nesses. Our first algorithm, heuristic UCT, incorporates prior ternal heuristic. Programs using UCT search have outper- knowledge in the form of a value function. The value function formed all previous Computer Go programs (Coulom 2006; can be learned offline, using a linear combination of a million Gelly et al. 2006). binary features, with weights trained by temporal-difference Monte-Carlo tree search algorithms suffer from two learning. Our second algorithm, UCT–RAVE, forms a rapid sources of inefficiency. First, when a position is encoun- online generalisation based on the value of moves. We ap- tered for the first time, no knowledge is available to guide plied our algorithms to the domain of 9 9 Computer Go, the search. -

Computer Go: from the Beginnings to Alphago Martin Müller, University of Alberta
Computer Go: from the Beginnings to AlphaGo Martin Müller, University of Alberta 2017 Outline of the Talk ✤ Game of Go ✤ Short history - Computer Go from the beginnings to AlphaGo ✤ The science behind AlphaGo ✤ The legacy of AlphaGo The Game of Go Go ✤ Classic two-player board game ✤ Invented in China thousands of years ago ✤ Simple rules, complex strategy ✤ Played by millions ✤ Hundreds of top experts - professional players ✤ Until 2016, computers weaker than humans Go Rules ✤ Start with empty board ✤ Place stone of your own color ✤ Goal: surround empty points or opponent - capture ✤ Win: control more than half the board Final score, 9x9 board ✤ Komi: first player advantage Measuring Go Strength ✤ People in Europe and America use the traditional Japanese ranking system ✤ Kyu (student) and Dan (master) levels ✤ Separate Dan ranks for professional players ✤ Kyu grades go down from 30 (absolute beginner) to 1 (best) ✤ Dan grades go up from 1 (weakest) to about 6 ✤ There is also a numerical (Elo) system, e.g. 2500 = 5 Dan Short History of Computer Go Computer Go History - Beginnings ✤ 1960’s: initial ideas, designs on paper ✤ 1970’s: first serious program - Reitman & Wilcox ✤ Interviews with strong human players ✤ Try to build a model of human decision-making ✤ Level: “advanced beginner”, 15-20 kyu ✤ One game costs thousands of dollars in computer time 1980-89 The Arrival of PC ✤ From 1980: PC (personal computers) arrive ✤ Many people get cheap access to computers ✤ Many start writing Go programs ✤ First competitions, Computer Olympiad, Ing Cup ✤ Level 10-15 kyu 1990-2005: Slow Progress ✤ Slow progress, commercial successes ✤ 1990 Ing Cup in Beijing ✤ 1993 Ing Cup in Chengdu ✤ Top programs Handtalk (Prof. -

ELF Opengo: an Analysis and Open Reimplementation of Alphazero
ELF OpenGo: An Analysis and Open Reimplementation of AlphaZero Yuandong Tian 1 Jerry Ma * 1 Qucheng Gong * 1 Shubho Sengupta * 1 Zhuoyuan Chen 1 James Pinkerton 1 C. Lawrence Zitnick 1 Abstract However, these advances in playing ability come at signifi- The AlphaGo, AlphaGo Zero, and AlphaZero cant computational expense. A single training run requires series of algorithms are remarkable demonstra- millions of selfplay games and days of training on thousands tions of deep reinforcement learning’s capabili- of TPUs, which is an unattainable level of compute for the ties, achieving superhuman performance in the majority of the research community. When combined with complex game of Go with progressively increas- the unavailability of code and models, the result is that the ing autonomy. However, many obstacles remain approach is very difficult, if not impossible, to reproduce, in the understanding of and usability of these study, improve upon, and extend. promising approaches by the research commu- In this paper, we propose ELF OpenGo, an open-source nity. Toward elucidating unresolved mysteries reimplementation of the AlphaZero (Silver et al., 2018) and facilitating future research, we propose ELF algorithm for the game of Go. We then apply ELF OpenGo OpenGo, an open-source reimplementation of the toward the following three additional contributions. AlphaZero algorithm. ELF OpenGo is the first open-source Go AI to convincingly demonstrate First, we train a superhuman model for ELF OpenGo. Af- superhuman performance with a perfect (20:0) ter running our AlphaZero-style training software on 2,000 record against global top professionals. We ap- GPUs for 9 days, our 20-block model has achieved super- ply ELF OpenGo to conduct extensive ablation human performance that is arguably comparable to the 20- studies, and to identify and analyze numerous in- block models described in Silver et al.(2017) and Silver teresting phenomena in both the model training et al.(2018).