Improvement of the Round Key Generation of AES
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Proceedings, Academy of Human Resource Development Conference, Volume I (Pp
TABLE OF CON T EN T S IN T RODU cti ONS Felix Rauner and Erica Smith ..........................................................................................13 Zhiqun Zhao ......................................................................................................................14 KEYNO T ES The apprenticeship approach: A way to overcome demarcations between vocational and higher education ....................................................................................19 Felix Rauner Apprenticeship as a model for the international architecture of TVET .......................33 Philipp Gonon School-enterprise cooperation in China’s vocational education and training ..........43 Zhiqun Zhao CHAP T ER I DEVELOP I NG CURR ic ULA AND QUAL I F ic A ti ON SYS T EMS Apprenticeship growth and quality in England .............................................................55 Richard Marsh Curriculum reforms in VET in Europe – a comparative view on France and Germany .....................................................................................................................59 Dietmar Frommberger and Léna Krichewsky Study on the implementation of the learning field curriculum in Germany ...............63 Han Xu Are we ready for the new round of TVET development based on China’s National Plan for Medium and Long-term Education Reform and Development (2010-2020) ................................................................................................67 Weiping Shi and Ying Kuang The link between the didactic approach -

Vice President's Meeting with People's Republic of China Vice Premier
W':' S C1 i NG'ON <!fOP ::!f!C~ / SENSITIVE / EYES ONLY MEMO~~DUM OF CONVERSA~ION SUBJECT: S~~ary of the Vice President ' s Meeting with People's Republic of China Vice Premier Deng Xiaoping PARTICIPP.. NTS : Vice President Walter Mondale Leonard Woodcock, U.S. Ambassador to the People's Republic of China David Aaron, Deputy Assistant to the President for National Security Affa~rs Richard Moe, Chief of Staff to the Vice President Denis Clift, Assistant to the Vice President for National Security Affairs Richard Holbrooke, Assistant Secretary of State for East Asian and Pacific Affair Michel Oksenberg, St"_aff Member I NSC Vice Premier Deng Xiaoping Huang Hua, Minister of Foreign Affairs Chai Zemin, People's Republic of China Ambassador to the United States Zhang Wenjin, Deputy Foreign Minister Han Xu, Director of American Depar~~ent Wei Yongqing, Director of Protocol Ji Chaozhu, Deputy Director of American Depart.:nent DATE, TD1E August 28, 1979; 9:30 a.m. - 12:00 Noon k'lD PLACE: The Great Hall of the People, Beijing, People's Republic of China Vi=e Premier Deng: I heard your speech ;vas war:nly ;.;elcomed. Vice ?res:":ient ~oncale: I W2.S thril2.ed by t.he opportunity to spea2< at your great unive.r·sity anc. -='0 speak to the people. It was an unprecedented occasion, and I t.hank you for that. cpport"..lni ty. DECLASSIFIED \E.O.12958, Sec.3.6 :~_R--I.~~__ NA~ ::T~31m;:J" ,TOP SECRET/SENSITIVE/ EYES ONLY 2 Vice Premier Deng: It was published in full in today ' s People's Daily. -

The Business of Sport in China
Paper size: 210mm x 270mm LONDON 26 Red Lion Square London WC1R 4HQ United Kingdom Tel: (44.20) 7576 8000 Fax: (44.20) 7576 8500 E-mail: [email protected] NEW YORK 111 West 57th Street New York The big league? NY 10019 United States Tel: (1.212) 554 0600 The business of sport in China Fax: (1.212) 586 1181/2 E-mail: [email protected] A report from the Economist Intelligence Unit HONG KONG 6001, Central Plaza 18 Harbour Road Wanchai Hong Kong Sponsored by Tel: (852) 2585 3888 Fax: (852) 2802 7638 E-mail: [email protected] The big league? The business of sport in China Contents Preface 3 Executive summary 4 A new playing field 7 Basketball 10 Golf 12 Tennis 15 Football 18 Outlook 21 © Economist Intelligence Unit 2009 1 The big league? The business of sport in China © 2009 Economist Intelligence Unit. All rights reserved. All information in this report is verified to the best of the author’s and the publisher’s ability. However, the Economist Intelligence Unit does not accept responsibility for any loss arising from reliance on it. Neither this publication nor any part of it may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior permission of the Economist Intelligence Unit. 2 © Economist Intelligence Unit 2009 The big league? The business of sport in China Preface The big league? The business of sport in China is an Economist Intelligence Unit briefing paper, sponsored by Mission Hills China. -
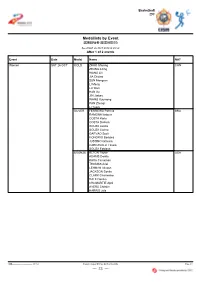
Medallists by Event 奖牌获得者(按项目排列) As of SAT 26 OCT 2019 at 20:52 After 1 of 2 Events
Basketball 篮球 Medallists by Event 奖牌获得者(按项目排列) As of SAT 26 OCT 2019 at 20:52 After 1 of 2 events Event Date Medal Name NAT Women SAT 26 OCT GOLD ZHAO Shuang CHN ZHANG Liting WANG Lili JIA Qiujiao SUN Mengran LI Meng LU Wen HAN Xu JIN Jiabao WANG Xuemeng PAN Zhenqi LI Yueru SILVER FERREIRA Patricia BRA RAMONA Isabela COSTA Karla COSTA Debora SOUZA Luana SOUZA Carina GARVAO Soeli HONORIO Barbara JUSTINO Gilmara CARCAVALLI Tassia SOUZA Fabiana BRONZE ALTON Taylor USA ADAMS Donita KAVA Cinnamon THOMAS Ariel LEHMAN Allyson JACKSON Santia CLARK Charmaine DALE Danika CROMARTIE April AYERS Christie HARRIS Jala BKB-------------------------------_93 1.0 Report Created SAT 26 OCT 2019 20:52 Page 1/1 — 33 — Hongshan Gymnasium Basketball 洪山体育馆 篮球 Men 男子 Tournament Summary 比赛总览 As of SAT 26 OCT 2019 at 20:51 Today's Games Phase Teams Start Time Location Final Q1 Q2 Q3 Q4 For 5th and 6th Places CGO VS GRE 13:00 Hongshan Gymnasium 62 - 78 15-18 15-15 15-32 17-13 For 3rd and 4th Places BRA VS CHN 15:30 Hongshan Gymnasium 64 - 68 14-16 19-15 15-17 16-20 Final USA VS LTU 19:00 Hongshan Gymnasium 83 - 91 20-14 15-30 20-28 28-19 Group A Games Points Class. Rank CHN USA CGO MGL QAT Played Won Lost For Against Diff Points 1 CHN 98-79 92-62 104-71 80-64 4 4 0 374 276 98 8 2 USA 79-98 79-76 88-86 71-68 4 3 1 317 328 -11 7 3 CGO 62-92 76-79 74-72 60-49 4 2 2 272 292 -20 6 4 MGL 71-104 86-88 72-74 75-67 4 1 3 304 333 -29 5 5 QAT 64-80 68-71 49-60 67-75 4 0 4 248 286 -38 4 Group B Games Points Class. -
Tech Glitch Helped Hunt Disappear a Chance to Heal, Look to the Future
The News Herald | Thursday, April 11, 2019 A1 POLICE SHOOT, KILL ARMED SUSPECT LOCAL | B1 PANAMA CITY LOCAL & STATE | B1 SIMS VETERANS GAME A BIG HIT Thursday, April 11, 2019 www.newsherald.com @The_News_Herald facebook.com/panamacitynewsherald 75¢ A chance to heal, Tech glitch look to the future helped Hunt disappear 3 days before the warrant confirmed and quadruple shooting, in hand, Hunt was nowhere ‘person of interest’ to be found and Patterson fl ed court before new ordered him held without sex charge could be bond on a charge of failure to confi rmed appear, because he left before the hearing was completed. By Mike Cazalas “We expect nothing but The News Herald great things from the elec- tronic filing system but PANAMA sometimes we just need to CITY — go with paper,” said State Michael Attorney Glenn Hess, whose Hunt didn’t prosecutor said at the begin- actually fail ning of the hearing that there to appear for was an active warrant for his pre-trial Hunt’s arrest for a new child Hunt hearing on sex charge. “This was one of charges of those times.” unlawful sexual acts with a One person died at the minor and aggravated assault scene of the quadruple shoot- three days before last week’s ing and three others remain in Rebuild Bay County, a coalition of religious groups and nonprofi ts, hosts Pray for Bay at Tommy Oliver quadruple shooting on Allen critical condition. Stadium on Wednesday. Local clergy and elected offi cials spoke about their experiences after Hurricane Avenue, for which he is a Courtroom video obtained Michael and gave inspirational words of faith. -

Han Dynasty Classicism and the Making of Early Medieval Literati Culture
University of Pennsylvania ScholarlyCommons Publicly Accessible Penn Dissertations 2013 In Pursuit of the Great Peace: Han Dynasty Classicism and the Making of Early Medieval Literati Culture Lu Zhao University of Pennsylvania, [email protected] Follow this and additional works at: https://repository.upenn.edu/edissertations Part of the Ancient History, Greek and Roman through Late Antiquity Commons, and the Asian History Commons Recommended Citation Zhao, Lu, "In Pursuit of the Great Peace: Han Dynasty Classicism and the Making of Early Medieval Literati Culture" (2013). Publicly Accessible Penn Dissertations. 826. https://repository.upenn.edu/edissertations/826 This paper is posted at ScholarlyCommons. https://repository.upenn.edu/edissertations/826 For more information, please contact [email protected]. In Pursuit of the Great Peace: Han Dynasty Classicism and the Making of Early Medieval Literati Culture Abstract This dissertation is focused on communities of people in the Han dynasty (205 B.C.-A.D. 220) who possessed the knowledge of a corpus of texts: the Five Classics. Previously scholars have understood the popularity of this corpus in the Han society as a result of stiff ideology and imperial propaganda. However, this approach fails to explain why the imperial government considered them effective to convey propaganda in the first place. It does not capture the diverse range of ideas in classicism. This dissertation concentrates on Han classicists and treats them as scholars who constantly competed for attention in intellectual communities and solved problems with innovative solutions that were plausible to their contemporaries. This approach explains the nature of the apocryphal texts, which scholars have previously referred to as shallow and pseudo-scientific. -

Clinical Characteristics and Outcomes of Hospitalised Patients with COVID-19 Treated in Hubei
Early View Original article Clinical characteristics and outcomes of hospitalised patients with COVID-19 treated in Hubei (epicenter) and outside Hubei (non- epicenter): A Nationwide Analysis of China Wen-hua Liang, Wei-jie Guan, Cai-chen Li, Yi-min Li, Heng-rui Liang, Yi Zhao, Xiao-qing Liu, Ling Sang, Ru-chong Chen, Chun-li Tang, Tao Wang, Wei Wang, Qi-hua He, Zi-sheng Chen, Sook-San Wong, Mark Zanin, Jun Liu, Xin Xu, Jun Huang, Jian-fu Li, Li-min Ou, Bo Cheng, Shan Xiong, Zhan- hong Xie, Zheng-yi Ni, Yu Hu, Lei Liu, Hong Shan, Chun-liang Lei, Yi-xiang Peng, Li Wei, Yong Liu, Ya-hua Hu, Peng Peng, Jian-ming Wang, Ji-yang Liu, Zhong Chen, Gang Li, Zhi-jian Zheng, Shao-qin Qiu, Jie Luo, Chang-jiang Ye, Shao-yong Zhu, Lin-ling Cheng, Feng Ye, Shi-yue Li, Jin-ping Zheng, Nuo-fu Zhang, Nan-shan Zhong, Jian-xing He Please cite this article as: Liang W-hua, Guan W-jie, Li C-chen, et al. Clinical characteristics and outcomes of hospitalised patients with COVID-19 treated in Hubei (epicenter) and outside Hubei (non-epicenter): A Nationwide Analysis of China. Eur Respir J 2020; in press (https://doi.org/10.1183/13993003.00562-2020). This manuscript has recently been accepted for publication in the European Respiratory Journal. It is published here in its accepted form prior to copyediting and typesetting by our production team. After these production processes are complete and the authors have approved the resulting proofs, the article will move to the latest issue of the ERJ online. -

Tokyo 2020 Women's Olympic Basketball Tournament 2020 Individual Statistics As of 07 Aug 2021 at 08:47
Tokyo 2020 Women's Olympic Basketball Tournament 2020 Individual Statistics As of 07 Aug 2021 at 08:47 POINTS (by average) POINTS (by total) RK No Name Team GP Total Avg. RK No Name Team GP Avg. Total 1 11 MEESSEMAN Emma BEL 4 107 26.8 1 11 MEESSEMAN Emma BEL 4 26.8 107 2 45 NDOUR Astou ESP 4 84 21.0 2 45 NDOUR Astou ESP 4 21.0 84 3 24 GWATHMEY Jazmon PUR 3 54 18.0 3 9 WILSON A'Ja USA 5 16.0 80 4 9 WILSON A'Ja USA 5 80 16.0 4 10 STEWART Breanna USA 5 15.2 76 5 10 STEWART Breanna USA 5 76 15.2 5 15 GRINER Brittney USA 5 13.8 69 6 14 LI Yueru CHN 4 59 14.8 6 7 GRUDA Sandrine FRA 5 13.6 68 6 5 MESTDAGH Kim BEL 4 59 14.8 7 8 TAKADA Maki JPN 5 13.4 67 8 3 KANG Leeseul KOR 3 43 14.3 8 52 MIYAZAWA Yuki JPN 5 13.2 66 9 15 GRINER Brittney USA 5 69 13.8 9 27 HAYASHI Saki JPN 5 12.8 64 10 7 GRUDA Sandrine FRA 5 68 13.6 10 12 ANDERSON Yvonne SRB 5 12.0 60 REBOUNDS ASSISTS RK No Name Team GP Total Off./Def. Avg. RK No Name Team GP Total Avg. 1 19 PARK Ji Su KOR 3 32 12/20 10.7 1 13 MACHIDA Rui JPN 5 69 13.8 2 11 MEESSEMAN Emma BEL 4 42 11/31 10.5 2 55 ALLEMAND Julie BEL 4 30 7.5 3 45 NDOUR Astou ESP 4 41 17/24 10.3 3 5 OUVINA Cristina ESP 4 26 6.5 4 32 DUGALIC Angela SRB 1 10 4/6 10.0 4 6 BIRD Sue USA 5 32 6.4 5 24 GIL Laura ESP 4 37 9/28 9.3 5 5 MITCHELL Leilani AUS 4 22 5.5 6 10 STEWART Breanna USA 5 46 5/41 9.2 6 11 MEESSEMAN Emma BEL 4 19 4.8 7 14 LI Yueru CHN 4 33 13/20 8.3 7 10 STEWART Breanna USA 5 23 4.6 8 88 AKAHO Himawari JPN 5 38 8/30 7.6 7 15 WILLIAMS Gabby FRA 5 23 4.6 8 15 GRINER Brittney USA 5 38 10/28 7.6 9 10 EBZERY Katie AUS 4 17 4.3 10 15 HAN Xu CHN 4 30 5/25 7.5 9 7 SHAO Ting CHN 4 17 4.3 FOULS DRAWN BLOCKED SHOTS RK No Name Team GP Total Avg. -
2018 USA World Cup Team ALPHABETICAL ROSTER
2018 USA BASKETBALL WORLD CUP TEAM Record Watch USA (4-0) vs. Belgium (3-1) Whoever scores the USA’s first Sept. 29, 2018 • ESPN News @ 5:30 p.m. (12:30 p.m EDT) point in its semifinal game will Santiago Martin Arena, San Cristobal de la Laguna, Spain have also scored the USA’s All-time USA World Cup record: 107-21 10,000th point in World Cup USA World Cup winning streak: 20-0 competition. USA vs. Belgium in World Cup play: 0-0 Belgium has never before qualified for a World Cup. 2018 USA World Cup Team ALPHABETICAL ROSTER NO NAME POS HGT WGT AGE TEAM SCHOOL HOMETOWN 6 Sue Bird G 5-9 150 37 Seattle Storm Connecticut ’02 Syosset, NY 14 Tina Charles C 6-4 192 29 New York Liberty Connecticut ’10 Jamaica, NY 7 Layshia Clarendon G 5-9 140 27 Connecticut Sun California ’13 San Bernardino, CA 11 Elena Delle Donne F/G 6-5 188 29 Washington Mystics Delaware ’13 Wilmington, DE 15 Brittney Griner C 6-9 205 27 Phoenix Mercury Baylor ‘13 Houston, TX 4 Jewell Loyd G 5-11 150 24 Seattle Storm Notre Dame ’15 Lincolnwood, IL 13 Nneka Ogwumike F 6-2 188 28 Los Angeles Sparks Stanford ‘12 Cypress, TX 5 Kelsey Plum G 5-8 145 24 Las Vegas Aces Washington ’17 Poway, CA 10 Breanna Stewart F 6-4 170 24 Seattle Storm Connecticut ‘16 North Syracuse, NY 12 Diana Taurasi G 6-0 164 36 Phoenix Mercury Connecticut ‘04 Chino, CA 8 Morgan Tuck F 6-2 200 24 Connecticut Sun Connecticut ‘16 Bolingbrook, IL 9 A’ja Wilson F 6-5 197 22 Las Vegas Aces South Carolina ’18 Hopkins, SC NUMERICAL ROSTER NO NAME POS HGT WGT AGE TEAM SCHOOL HOMETOWN 4 Jewell Loyd G 5-11 150 24 Seattle -
Results CHN 76 Vs 74
Saitama Super Arena Basketball さいたまスーパーアリーナ バスケットボール / Basketball Super Arena de Saitama Women 女子 / Femmes FRI 30 JUL 2021 Preliminary Round Group C Start Time: 21:00 予選ラウンドグループC / Tour préliminaire groupe C Results 結果 / Résultats Game 24 CHN 76 vs 74 AUS (27-19, 11-19, 17-9, 21-27) Game Duration: 1:49 Crew Chief: KALLIO Matthew (CAN) Commissioner: SCHAER Gabriela (CRC) Umpires: FORSBERG Maj (DEN); AL SHUWAILI Ahmed (IRQ) Q1 Q2 Q3 Q4 Scoring by 5 min intervals: CHN 16 27 31 38 48 55 64 76 AUS 9 19 30 38 42 47 55 74 CHN - China Field Goals 2 Points 3 Points Free Throws Rebounds No. Name MIN AS TO ST BS PF FD +/- PTS M / A % M / A % M / A % M / A % OR DR TOT 3 YANG Liwei 29:52 4/9 44 2/4 50 2/5 40 0/1 0 2 2 2 5 2 1 -6 10 *4 LI Yuan 14:17 1/6 17 0/3 0 1/3 33 1 1 2 -4 3 5 WANG Siyu 25:43 6/9 67 5/8 63 1/1 100 7/9 78 3 3 5 2 3 7 6 20 6 WU Tongtong DNP *7 SHAO Ting (C) 22:42 3/7 43 3/6 50 0/1 0 2/2 100 2 6 8 2 2 2 3 1 4 8 8 ZHANG Ru DNP *9 LI Meng 26:29 4/9 44 3/4 75 1/5 20 2/2 100 2 2 7 3 2 1 6 11 *10 PAN Zhenqi 3:28 1 0 11 HUANG Sijing 23:38 1/7 14 0/3 0 1/4 25 2 2 4 2 2 1 -5 3 13 SUN Mengran 14:08 1/3 33 0/1 0 1/2 50 3 3 1 1 1 1 1 3 3 *14 LI Yueru 27:44 4/7 57 4/7 57 4/5 80 3 4 7 5 3 1 1 3 4 12 12 15 HAN Xu 11:59 2/3 67 2/3 67 2/2 100 4 4 1 3 3 -7 6 Team / Coach 4 4 8 2 Totals 26/60 43 19/39 49 7/21 33 17/21 81 11 31 42 24 21 4 4 17 18 2 76 Coach XU Limin Assistant Coach ZHENG Wei JIA Nan AUS - Australia Field Goals 2 Points 3 Points Free Throws Rebounds No. -

2016-Commencement-Program.Pdf
Duke University Commencement One Hundred Sixty-Fourth Commencement Sunday, the Fifteenth of May, Two Thousand and Sixteen Notes on Academic Dress Academic dress had its origin in the Middle Ages. When the European universities were taking form in the thirteenth and fourteenth centuries, scholars were also clerics, and they adopted robes similar to those of their monastic Mace and Chain of Office orders. Caps were a necessity in drafty build- ings, and copes or capes with hoods attached Again at commencement, ceremonial use is were needed for warmth. As the control of made of two important insignia given to Duke universities gradually passed from the church, University in memory of Benjamin N. Duke. academic costume began to take on brighter Both the mace and chain of office are the hues and to employ varied patterns in cut and gifts of anonymous donors and of the Mary color of gown and type of headdress. Duke Biddle Foundation. They were designed and executed by Professor Kurt J. Matzdorf The use of academic costume in the United of New Paltz, New York, and were dedicated States has been continuous since Colonial and first used at the inaugural ceremonies times, but a clear protocol did not emerge until of President Sanford in 1970. an intercollegiate commission in 1893 recom- mended a uniform code. In this country, the The Mace, the symbol of authority of the design of a gown varies with the degree held. University, is made of sterling silver through- The bachelor’s gown is relatively simple with Significance of Colors out. It is thirty-seven inches long and weighs long pointed sleeves as its distinguishing about eight pounds. -

Vascular Discovery: from Genes to Medicine 2019 Scientific Sessions
American Heart Association® Vascular Discovery: For information on upcoming From Genes to Medicine American Heart Association Scientific Conferences, visit professional.heart.org Cardiovascular diseases afflict people of all races, ethnicities, genders, religions, ages, sexual orientations, national origins and disabilities. The American Heart Association is committed to ensuring that our workforce and volunteers reflect the world’s diverse population. We know that such diversity will enrich us with VASCULAR DISCOVERY: the talent, energy, perspective and inspiration we need to achieve our mission: From Genes to Medicine building healthier lives, free of cardiovascular diseases and stroke. Scientific Sessions 2019 Final Program May 14-16, 2019 | Boston Marriott Copley Place Hotel | Boston, Massachusetts American Heart Association® Vascular Discovery: This annual scientific meeting of the American Heart Association is sponsored by the Council on Arteriosclerosis, From Genes to Medicine Thrombosis and Vascular Biology, Council on Peripheral Vascular Disease, and Council on Genomic and Precision Medicine, in collaboration with the Society of Vascular Surgery’s Vascular Research Initiatives Conference, and National Center 7272 Greenville Avenue the American Venous Forum. Dallas, Texas 75231-4596 ©2019, American Heart Association, Inc. All rights reserved. Unauthorized use prohibited. 3/19JN0960 Co-Director of the Fireman Vascular Center Department of Medicine Massachusetts General Hospital The Cardiology Division and the Fireman Vascular Center at the Massachusetts General Hospital are seeking an academic and clinical leader to serve as the Co-Director of the Fireman Vascular Center. Along with the Division Chief for Vascular Surgery, this individual will be jointly responsible for the full scope of clinical, research and educational activities of the Fireman Vascular Center as well as collaborative activities with the other components of the Center.