M/L, H-Alpha Rotation Curves, and HI Measurements for 329 Nearby
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Messier Objects
Messier Objects From the Stocker Astroscience Center at Florida International University Miami Florida The Messier Project Main contributors: • Daniel Puentes • Steven Revesz • Bobby Martinez Charles Messier • Gabriel Salazar • Riya Gandhi • Dr. James Webb – Director, Stocker Astroscience center • All images reduced and combined using MIRA image processing software. (Mirametrics) What are Messier Objects? • Messier objects are a list of astronomical sources compiled by Charles Messier, an 18th and early 19th century astronomer. He created a list of distracting objects to avoid while comet hunting. This list now contains over 110 objects, many of which are the most famous astronomical bodies known. The list contains planetary nebula, star clusters, and other galaxies. - Bobby Martinez The Telescope The telescope used to take these images is an Astronomical Consultants and Equipment (ACE) 24- inch (0.61-meter) Ritchey-Chretien reflecting telescope. It has a focal ratio of F6.2 and is supported on a structure independent of the building that houses it. It is equipped with a Finger Lakes 1kx1k CCD camera cooled to -30o C at the Cassegrain focus. It is equipped with dual filter wheels, the first containing UBVRI scientific filters and the second RGBL color filters. Messier 1 Found 6,500 light years away in the constellation of Taurus, the Crab Nebula (known as M1) is a supernova remnant. The original supernova that formed the crab nebula was observed by Chinese, Japanese and Arab astronomers in 1054 AD as an incredibly bright “Guest star” which was visible for over twenty-two months. The supernova that produced the Crab Nebula is thought to have been an evolved star roughly ten times more massive than the Sun. -

A Search for Transiting Extrasolar Planets in the Open Cluster NGC 4755
ResearchOnline@JCU This file is part of the following reference: Jayawardene, Bandupriya S. (2015) A search for transiting extrasolar planets in the open cluster NGC 4755. DAstron thesis, James Cook University. Access to this file is available from: http://researchonline.jcu.edu.au/41511/ The author has certified to JCU that they have made a reasonable effort to gain permission and acknowledge the owner of any third party copyright material included in this document. If you believe that this is not the case, please contact [email protected] and quote http://researchonline.jcu.edu.au/41511/ A SEARCH FOR TRANSITING EXTRASOLAR PLANETS IN THE OPEN CLUSTER NGC 4755 by Bandupriya S. Jayawardene A thesis submitted in satisfaction of the requirements for the degree of Doctor of Astronomy in the Faculty of Science, Technology and Engineering June 2015 James Cook University Townsville - Australia i STATEMENT OF ACCESS I the undersigned, author of this work, understand that James Cook University will make this thesis available for use within the University Library and, via the Australian Digital Thesis network, for use elsewhere. I understand that, as an unpublished work, a thesis has significant protection under the Copyright Act and; I do not wish to place any further restriction on access to this work. 2 STATEMENT OF SOURCES DECLARATION I declare that this thesis is my own work and has not been submitted in any form for another degree or diploma at any University or other institution of tertiary education. Information derived from the published or unpublished work of others has been acknowledged in the text and list of references is given. -

And – Objektauswahl NGC Teil 1
And – Objektauswahl NGC Teil 1 NGC 5 NGC 49 NGC 79 NGC 97 NGC 184 NGC 233 NGC 389 NGC 531 Teil 1 NGC 11 NGC 51 NGC 80 NGC 108 NGC 205 NGC 243 NGC 393 NGC 536 NGC 13 NGC 67 NGC 81 NGC 109 NGC 206 NGC 252 NGC 404 NGC 542 Teil 2 NGC 19 NGC 68 NGC 83 NGC 112 NGC 214 NGC 258 NGC 425 NGC 551 NGC 20 NGC 69 NGC 85 NGC 140 NGC 218 NGC 260 NGC 431 NGC 561 NGC 27 NGC 70 NGC 86 NGC 149 NGC 221 NGC 262 NGC 477 NGC 562 NGC 29 NGC 71 NGC 90 NGC 160 NGC 224 NGC 272 NGC 512 NGC 573 NGC 39 NGC 72 NGC 93 NGC 169 NGC 226 NGC 280 NGC 523 NGC 590 NGC 43 NGC 74 NGC 94 NGC 181 NGC 228 NGC 304 NGC 528 NGC 591 NGC 48 NGC 76 NGC 96 NGC 183 NGC 229 NGC 317 NGC 529 NGC 605 Sternbild- Zur Objektauswahl: Nummer anklicken Übersicht Zur Übersichtskarte: Objekt in Aufsuchkarte anklicken Zum Detailfoto: Objekt in Übersichtskarte anklicken And – Objektauswahl NGC Teil 2 NGC 620 NGC 709 NGC 759 NGC 891 NGC 923 NGC 1000 NGC 7440 NGC 7836 Teil 1 NGC 662 NGC 710 NGC 797 NGC 898 NGC 933 NGC 7445 NGC 668 NGC 712 NGC 801 NGC 906 NGC 937 NGC 7446 Teil 2 NGC 679 NGC 714 NGC 812 NGC 909 NGC 946 NGC 7449 NGC 687 NGC 717 NGC 818 NGC 910 NGC 956 NGC 7618 NGC 700 NGC 721 NGC 828 NGC 911 NGC 980 NGC 7640 NGC 703 NGC 732 NGC 834 NGC 912 NGC 982 NGC 7662 NGC 704 NGC 746 NGC 841 NGC 913 NGC 995 NGC 7686 NGC 705 NGC 752 NGC 845 NGC 914 NGC 996 NGC 7707 NGC 708 NGC 753 NGC 846 NGC 920 NGC 999 NGC 7831 Sternbild- Zur Objektauswahl: Nummer anklicken Übersicht Zur Übersichtskarte: Objekt in Aufsuchkarte anklicken Zum Detailfoto: Objekt in Übersichtskarte anklicken Auswahl And SternbildübersichtAnd -

Stellar Death in the Nearby Universe
Stellar Death in the Nearby Universe DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Thomas Warren-Son Holoien Graduate Program in Astronomy The Ohio State University 2017 Dissertation Committee: Professor Krzysztof Z. Stanek, Advisor Professor Christopher S. Kochanek, Co-Advisor Professor Todd A. Thompson Copyright by Thomas Warren-Son Holoien 2017 Abstract The night sky is replete with transient and variable events that help shape our universe. The violent, explosive deaths of stars represent some of the most energetic of these events, as a single star is able to outshine billions during its final moments. Aside from imparting significant energy into their host environments, stellar deaths are also responsible for seeding heavy elements into the universe, regulating star formation in their host galaxies, and affecting the evolution of supermassive black holes at the centers of their host galaxies. The large amount of energy output during these events allows them to be seen from billions of lightyears away, making them useful observational probes of physical processes important to many fields of astronomy. In this dissertation I present a series of observational studies of two classes of transients associated with the deaths of stars in the nearby universe: tidal disruption events (TDEs) and supernovae (SNe). Discovered by the All-Sky Automated Survey for Supernovae (ASAS-SN), the objects I discuss were all bright and nearby, and were subject to extensive follow-up observational campaigns. In the first three studies, I present observational data and theoretical models of ASASSN-14ae, ASASSN-14li, and ASASSN-15oi, three TDEs discovered by ASAS-SN and three ii of the most well-studied TDEs ever discovered. -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

Publications of Richard W. Pogge
Publications Richard William Pogge Updated: 2021 March 10 Doctoral Dissertation “The Circumnuclear Environment of Nearby, Non-Interacting Seyfert Galaxies”, University of California, Santa Cruz, June 1988. (Abstract published in PASP, 100, 1296, 1988. See also #7, 8, 10, 11, & 12 below.) Papers Published in Peer-RevieWed Journals 1. “X-Ray, Radio, and Infrared Observations of the Rapid Burster (MXB 1730-335) During 1979 and 1980”, LaWrence, A., et al. (52 authors), 1983, ApJ, 267, 301 2. “The Spectra of Narrow-Line Seyfert 1 Galaxies”, Osterbrock, Donald E., & Pogge, Richard W. 1985, ApJ, 297, 166 3. “The Extended Narrow Emission-Line Region of NGC 7469 Revisited”, DeRobertis, M.M. Pogge, R.W. 1986, AJ, 91, 1026 4. “Star Forming Regions in Gas-Rich Lenticulars. I. Ha Imaging of an Initial Sample of Galaxies”, Pogge, Richard W., & Eskridge, Paul B. 1987, AJ, 93, 291 5. “FY Aquilae and the Gamma-Ray Burst Event of 1979 March 31”, Hartmann, Dieter, & Pogge, Richard W. 1987, ApJ, 318, 363 6. “Optical Spectra of Narrow Emission Line Palomar-Green Galaxies”, Osterbrock, Donald E., & Pogge, Richard W. 1987, ApJ, 323, 108 7. “The circumnuclear environment of the nearby non-interacting Seyfert galaxies NGC 5273 and NGC 3516”, Pogge, R. W., 1988, LNP, 307, 46 8. “An Extended Ionizing Radiation Cone from the Nucleus of the Seyfert 2 Galaxy NGC 1068”, Pogge, Richard W. 1988, ApJ, 328, 519 9. “Extended Ionized Gas in the Seyfert 2 Galaxy NGC 4388”, Pogge, Richard W. 1988, ApJ, 332, 702 10. “OTS 1809+314 and the Gamma-Ray Burst GB 790325b”, Hartmann, Dieter, Pogge, Richard W., Hurley, Kevin, Vrba, Frederick J., & Jennings, Mark C. -

Target Selection for the SDSS-IV APOGEE-2 Survey
The Astronomical Journal, 154:198 (18pp), 2017 November https://doi.org/10.3847/1538-3881/aa8df9 © 2017. The American Astronomical Society. All rights reserved. Target Selection for the SDSS-IV APOGEE-2 Survey G. Zasowski1,2, R. E. Cohen2, S. D. Chojnowski3 , F. Santana4 , R. J. Oelkers5 , B. Andrews6 , R. L. Beaton7 , C. Bender8, J. C. Bird5, J. Bovy9 , J. K. Carlberg2 , K. Covey10 , K. Cunha8,11, F. Dell’Agli12, Scott W. Fleming2 , P. M. Frinchaboy13 , D. A. García-Hernández12, P. Harding14 , J. Holtzman3 , J. A. Johnson15, J. A. Kollmeier7 , S. R. Majewski16 , Sz. Mészáros17,27, J. Munn18 , R. R. Muñoz4, M. K. Ness19, D. L. Nidever20 , R. Poleski15,21, C. Román-Zúñiga22 , M. Shetrone23 , J. D. Simon7, V. V. Smith20, J. S. Sobeck24, G. S. Stringfellow25 , L. Szigetiáros17, J. Tayar15 , and N. Troup16,26 1 Department of Physics & Astronomy, University of Utah, Salt Lake City, UT 84112, USA; [email protected] 2 Space Telescope Science Institute, Baltimore, MD 21218, USA 3 Department of Astronomy, New Mexico State University, Las Cruces, NM 88001, USA 4 Departamento de Astronomía, Universidad de Chile, Santiago, Chile 5 Department of Physics & Astronomy, Vanderbilt University, Nashville, TN 37235, USA 6 PITT PACC, Department of Physics & Astronomy, University of Pittsburgh, Pittsburgh, PA 15260, USA 7 The Observatories of the Carnegie Institution for Science, Pasadena, CA 91101, USA 8 Steward Observatory, The University of Arizona, Tucson, AZ 85719, USA 9 Department of Astronomy and Astrophysics & Dunlap Institute for Astronomy and -

A Comprehensive Field Guide to the Ngc Volume 1: Autumn/Winter (Andromeda-Eridanus)
A COMPREHENSIVE FIELD GUIDE TO THE NGC VOLUME 1: AUTUMN/WINTER (ANDROMEDA-ERIDANUS) BHAVESH JIVAN-KALA PAREKH A COMPREHENSIVE FIELD GUIDE TO THE NGC VOLUME 2: AUTUMN/WINTER (FORNAX-VOLANS) BHAVESH JIVAN-KALA PAREKH A COMPREHENSIVE FIELD GUIDE TO THE NGC VOLUME 3: SPRING/SUMMER (ANTILA-INDUS) BHAVESH JIVAN-KALA PAREKH A COMPREHENSIVE FIELD GUIDE TO THE NGC VOLUME 4: SPRING/SUMMER (LEO-VULPECULA) BHAVESH JIVAN-KALA PAREKH Front Cover images: Vol 1: NGC 772/ARP 78 Vol 2: NGC 7317-18-19-20 Stephen’s Quintet Vol 3: NGC 4038-39/ARP 244 Antennae Galaxies Vol 4: NGC 5679/ARP 274 Galaxy Triplet Three of the galaxies in this famous grouping, Stephan's Quintet, A beautiful composite image of two colliding galaxies, the A system of three galaxies that appear to be partially overlapping in NGC 772, a spiral galaxy, has much in common with our home are distorted from their gravitational interactions with one another. Antennae galaxies, located about 62 million light-years from Earth. the image, although they may be at somewhat different distances. galaxy, the Milky Way. Each boasts a few satellite galaxies, small One member of the group, NGC 7320 (upper right) is actually The Antennae galaxies take their name from the long antenna-like The spiral shapes of two of these galaxies appear mostly intact. galaxies that closely orbit and are gravitationally bound to their seven times closer to Earth than the rest. "arms," seen in wide-angle views of the system. These features The third galaxy (to the far left) is more compact, but shows were produced by tidal forces generated in the collision, which parent galaxies. -
Veil Nebula Veil Nebula 20 51 28 +31 00 06 ‐ 3° Cygnus Supernova Remnant
Downloaded from www.faintfuzzies.com 1 www.deepskyforum.com Downloaded from www.faintfuzzies.com 2 www.deepskyforum.com Deep Sky Forum 2012 Objects of the Week Compiled and edited by Alvin H. Huey www.faintfuzzies.com Last updated: Feb 04, 2013 Downloaded from www.faintfuzzies.com 3 www.deepskyforum.com www.faintfuzzies.com First edition: February 2013 All Maps by MegaStarTM v5 All DSS images (Digital Sky Survey) http://archive.stsci.edu/dss/acknowledging.html All SDSS images (Sloan Digital Sky Survey) http://www.sdss.org/ Downloaded from www.faintfuzzies.com 4 www.deepskyforum.com Table of Contents Forward 6 How to Use the Atlas 7 OOTW List 8 OOTW Atlas 12 Downloaded from www.faintfuzzies.com 5 www.deepskyforum.com Forward This month marks the one year anniversary of DeepSkyForum.com and we couldn't be more pleased! Over the past year DSF has grown beyond our wildest expectations with nearly 300 members and 1500+ posts discussing deep sky observing! It's all positive news and we're very happy! It wouldn't have been possible if it weren't for you, our members. You folks have accepted DSF with open arms and made it a premier destination for deep sky observing discussion. DSF has become such a huge repository of information in such a short time and for that we're forever grateful. It’s become difficult to go and observe without first stopping by the site. When we first started DSF we introduced something that many of you have been a part of. Every week on Sunday, a new and interesting object is chosen to be the Object of the Week (OOTW). -

The HI Distribution of Spiral Galaxies in the Cluster a 262 Bravo-Alfaro, H.; Szomoru, A.; Cayatte, V.; Balkowski, C.; Sancisi, R
University of Groningen The HI distribution of spiral galaxies in the cluster A 262 Bravo-Alfaro, H.; Szomoru, A.; Cayatte, V.; Balkowski, C.; Sancisi, R. Published in: Astronomy & astrophysics supplement series DOI: 10.1051/aas:1997281 IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish to cite from it. Please check the document version below. Document Version Publisher's PDF, also known as Version of record Publication date: 1997 Link to publication in University of Groningen/UMCG research database Citation for published version (APA): Bravo-Alfaro, H., Szomoru, A., Cayatte, V., Balkowski, C., & Sancisi, R. (1997). The HI distribution of spiral galaxies in the cluster A 262. Astronomy & astrophysics supplement series, 126(3), 537-546. https://doi.org/10.1051/aas:1997281 Copyright Other than for strictly personal use, it is not permitted to download or to forward/distribute the text or part of it without the consent of the author(s) and/or copyright holder(s), unless the work is under an open content license (like Creative Commons). The publication may also be distributed here under the terms of Article 25fa of the Dutch Copyright Act, indicated by the “Taverne” license. More information can be found on the University of Groningen website: https://www.rug.nl/library/open-access/self-archiving-pure/taverne- amendment. Take-down policy If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. Downloaded from the University of Groningen/UMCG research database (Pure): http://www.rug.nl/research/portal. -

DSO List V2 Current
7000 DSO List (sorted by constellation - magnitude) 7000 DSO List (sorted by constellation - magnitude) - from SAC 7.7 database NAME OTHER TYPE CON MAG S.B. SIZE RA DEC U2K Class ns bs SAC NOTES M 31 NGC 224 Galaxy AND 3.4 13.5 189' 00 42.7 +41 16 60 Sb Andromeda Galaxy;Local Group;nearest spiral NGC 7686 OCL 251 Opn CL AND 5.6 - 15' 23 30.1 +49 08 88 IV 1 p 20 6.2 H VIII 69;12* mags 8...13 NGC 752 OCL 363 Opn CL AND 5.7 - 50' 01 57.7 +37 40 92 III 1 m 60 9 H VII 32;Best in RFT or binocs;Ir scattered cl 70* m 8... M 32 NGC 221 Galaxy AND 8.1 12.4 8.5' 00 42.7 +40 52 60 E2 Companion to M31; Member of Local Group M 110 NGC 205 Galaxy AND 8.1 14 19.5' 00 40.4 +41 41 60 SA0 M31 Companion;UGC 426; Member Local Group NGC 272 OCL 312 Opn CL AND 8.5 - 00 51.4 +35 49 90 IV 1 p 8 9 NGC 7662 PK 106-17.1 Pln Neb AND 8.6 5.6 17'' 23 25.9 +42 32 88 4(3) 14 Blue Snowball Nebula;H IV 18;Barnard-cent * variable? NGC 956 OCL 377 Opn CL AND 8.9 - 8' 02 32.5 +44 36 62 IV 1 p 30 9 NGC 891 UGC 1831 Galaxy AND 9.9 13.6 13.1' 02 22.6 +42 21 62 Sb NGC 1023 group;Lord Rosse drawing shows dark lane NGC 404 UGC 718 Galaxy AND 10.3 12.8 4.3' 01 09.4 +35 43 91 E0 Mirach's ghost H II 224;UGC 718;Beta AND sf 6' IC 239 UGC 2080 Galaxy AND 11.1 14.2 4.6' 02 36.5 +38 58 93 SBa In NGC 1023 group;vsBN in smooth bar;low surface br NGC 812 UGC 1598 Galaxy AND 11.2 12.8 3' 02 06.9 +44 34 62 Sbc Peculiar NGC 7640 UGC 12554 Galaxy AND 11.3 14.5 10' 23 22.1 +40 51 88 SBbc H II 600;nearly edge on spiral MCG +08-01-016 Galaxy AND 12 - 1.0' 23 59.2 +46 53 59 Face On MCG +08-01-018 -
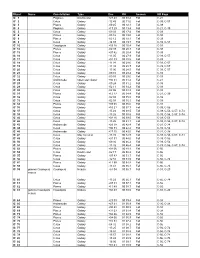
HB-NGC Index
Object Name Constellation Type Dec RA Season HB Page IC 1 Pegasus Double star +27 43 00 08.4 Fall C-21 IC 2 Cetus Galaxy -12 49 00 11.0 Fall C-39, C-57 IC 3 Pisces Galaxy -00 25 00 12.1 Fall C-39 IC 4 Pegasus Galaxy +17 29 00 13.4 Fall C-21, C-39 IC 5 Cetus Galaxy -09 33 00 17.4 Fall C-39 IC 6 Pisces Galaxy -03 16 00 19.0 Fall C-39 IC 8 Pisces Galaxy -03 13 00 19.1 Fall C-39 IC 9 Cetus Galaxy -14 07 00 19.7 Fall C-39, C-57 IC 10 Cassiopeia Galaxy +59 18 00 20.4 Fall C-03 IC 12 Pisces Galaxy -02 39 00 20.3 Fall C-39 IC 13 Pisces Galaxy +07 42 00 20.4 Fall C-39 IC 16 Cetus Galaxy -13 05 00 27.9 Fall C-39, C-57 IC 17 Cetus Galaxy +02 39 00 28.5 Fall C-39 IC 18 Cetus Galaxy -11 34 00 28.6 Fall C-39, C-57 IC 19 Cetus Galaxy -11 38 00 28.7 Fall C-39, C-57 IC 20 Cetus Galaxy -13 00 00 28.5 Fall C-39, C-57 IC 21 Cetus Galaxy -00 10 00 29.2 Fall C-39 IC 22 Cetus Galaxy -09 03 00 29.6 Fall C-39 IC 24 Andromeda Open star cluster +30 51 00 31.2 Fall C-21 IC 25 Cetus Galaxy -00 24 00 31.2 Fall C-39 IC 29 Cetus Galaxy -02 11 00 34.2 Fall C-39 IC 30 Cetus Galaxy -02 05 00 34.3 Fall C-39 IC 31 Pisces Galaxy +12 17 00 34.4 Fall C-21, C-39 IC 32 Cetus Galaxy -02 08 00 35.0 Fall C-39 IC 33 Cetus Galaxy -02 08 00 35.1 Fall C-39 IC 34 Pisces Galaxy +09 08 00 35.6 Fall C-39 IC 35 Pisces Galaxy +10 21 00 37.7 Fall C-39, C-56 IC 37 Cetus Galaxy -15 23 00 38.5 Fall C-39, C-56, C-57, C-74 IC 38 Cetus Galaxy -15 26 00 38.6 Fall C-39, C-56, C-57, C-74 IC 40 Cetus Galaxy +02 26 00 39.5 Fall C-39, C-56 IC 42 Cetus Galaxy -15 26 00 41.1 Fall C-39, C-56, C-57, C-74 IC