DOCSLIB.ORG

08-PQ+Heap+Trie Posted.Pptx

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
08-PQ+Heap+Trie Posted.Pptx What is a Priority Queue! A list of items where each item is given a priority value! •!priority values are usually numbers! •!priority values should have relative order (e.g., <)! •!dequeue operation differs from that of a queue or dictionary: item dequeued is always one with highest priority! Method! Description! Lecture 8: Priority Queue! enqueue(item)! insert item by its priority! Heap! Item &dequeuemax()! remove highest priority element! Item& findmax()! return a reference to highest Trie! priority element ! Huffman Coding! size()! number of elements in pqueue! empty()! checks if pqueue has no elements! No search()!! Priority Queue Examples! Priority Queue: Other Examples! Emergency call center:! •! operators receive calls and assign levels of urgency! Scheduling in general:! •! lower numbers indicate higher urgency! •!shortest job first print queue! •! calls are dispatched (or not dispatched) by computer to police •!shortest job first cpu queue! squads based on urgency! •!discrete events simulation (e.g., computer games)! Example:! Priority value used 1.!Level 2 call comes in! as array index! 2.!Level 2 call comes in! 3.!Level 1 call comes in! 0! 4.!A call is dispatched! 1! 5.!Level 0 call comes in! 6.!A call is disptached! 2! Priority Queue Implementations! BST as Priority Queue! Where is the smallest/largest item in a BST?! Implementation! dequeuemax()! enqueue()! Time complexity of enqueue() and dequeuemax():! •!enqueue(): O(log N)! Unsorted list! O(N)! O(1)! •!dequeuemax(): O(log N)! Sorted list! O(1)! O(N)! Why not just use a BST for priority queue?! Array of linked list! (but only for a small O(1)! O(1)! number of priorities)! Heap! O(log n)! O(log n)! Heaps! Heaps Implementation! A binary heap is a complete binary tree! A binary heap is a complete binary tree! •! can be efficiently stored as an array! A non-empty maxHeap T is an ordered •! if root is at node 0:! tree whereby:! •! a node at index i has children at indices 2i+1 and 2i+2! •! a node at index i has parent at index floor((i–1)/2)! •!the key in the root of T is !" •! what happens when array is full?! heap:! the keys in every subtree of T! •!every subtree of T is a maxHeap! •!(the keys of nodes across subtrees" have no required relationship)! •!a size variable keeps the number of" nodes in heap (not per subtree)! •!a minHeap is similarly defined! maxHeap::dequeuemax()! maxHeap::dequeuemax()! Save the max item at root, to be returned! Move the item in the rightmost leaf node to root! 1059!! 10! 5! 9! •! since the heap is a complete binary tree," the rightmost leaf node is always at the last index! 59! 6! 9! 6! 9! 6! 5! 6! •! swap(heap[0], heap(--size));! The tree is no longer a heap at this point! 3! 2! 5! 3! 2! 5! 3! 2! 3! 2! Trickle down the recently moved item at the root to its proper place to restore heap property! 1059!! 10! 5! 9! •! for each subtree, recursively, if the root has a smaller 95! 9! 9! 5! search key than either of its children, swap the item" in the root with that of the larger child! 6! 6! 6! 6! 3! 3! 3! 3! Complexity: O(log n)! 2! 2! 2! 2! 105!! 5! 10! return:! 10! Top Down Heapify! void maxHeap::! maxHeap::enqueue() ! trickleDown(int idx) {! 159!! for (j = 2*idx+1; j <= size; j = 2*j+1) {! Insert newItem into the bottom of the tree! if (j < size-1 && heap[j] < heap[j+1]) j++;! •! heap[size++] = newItem;! if (heap[idx] >= heap[j]) break; ! 5! 1596!! swap(heap[idx], heap[j]); idx = j;! The tree may no longer be a heap at this point! }! Percolate newItem up to an appropriate spot 3! 2! 156!! }! in the tree to restore the heap property! 15! Pass index (idx) of array element that needs to be trickled down! 9! Complexity: O(log n)! 5! Swap the key in the given node with the largest key among the 1569!! node’s children, moving down to that child, until either! 3! •! we reach a leaf node, or! •! both children have smaller (or equal) key! 2! 156!! Last node is at heap.size! maxHeap::enqueue()! Bottom Up Heapify! void maxHeap::! 9! 9! 9! 15! percolateUp(int idx) {! while (idx >= 1 && heap[(idx-1)/2] < heap[idx]){! swap(heap[idx], heap[(idx-1)/2]); ! 5! 6! 5! 6! 5! 15! 5! 9! idx = (idx-1)/2;! }! }! 3! 2! 3! 2! 15! 3! 2! 6! 3! 2! 6! Pass index (idx) of array element that needs to be percolated up! 9! 9! 9! 15! Swap the key in the given node with the key of its parent, " 5! 5! 5! 5! moving up to parent until:! 6! 6! 15! 9! •! we reach the root, or! 3! 3! 3! 3! •! the parent has a larger (or equal) key! 2! 2! 2! 2! Root is at position 0! 15! 6! 6! Heap Implementation! Trie! trie: from retrieval, originally pronounced void maxHeap::! enqueue():! to rhyme with retrieval, now commonly enqueue(Item newItem) {! •! put item at the end of pronounced to rhyme with “try”, to heap[size] = newItem;! the priority queue! differentiate from tree! o! t! percolateUp(size);! •! use percolateUp() size++! to find proper position! A trie is a tree that uses parts of the key, }! as opposed to the whole key, to perform n! w! i! o! search! Item maxHeap::! dequeuemax():! dequeuemax() {! •! remove root! Whereas a tree associates keys with e! l! p! swap(heap[0], heap[""size]);! •! take item from end of nodes, a trie associates keys with edges" trickleDown(0);! array and place at root! (though implementation may store the return heap[size];! •! use trickleDown() keys in the nodes)! }! to find proper position! Example: the trie on the right encodes this set of strings: {on, owe, owl, tip, to}! Trie! Partial Match! A trie is useful for doing partial match search:! For S a set of strings from an alphabet (not necessarily Latin alphabets) where none of longest-prefix match: a search for" the strings is a prefix of another, a trie of S o! t! “tin” would return “tip”! o! t! is an ordered tree such that:! •! implementation:! continue to search until a mismatch! •! each edge of the tree is labeled with symbols n! w! i! o! n! w! i! o! from the alphabet! approximate match: allowing for" •! the labels can be stored either at" the children nodes or at the parent node! one error, a search for “oil” would" p! e! l! p! return “owl” in this example! e! l! •! the ordering of edges attached to children of a node follows the natural ordering of the alphabet! •! labels of edges on the path from the root to any node in the tree forms a prefix of a string in S ! Useful for suggesting alternatives to misspellings! Trie Deletion! String Encoding! How many bits do we need to encode this By post-order traversal, remove an example string:! internal node only if it’s also a leaf node! If a woodchuck could chuck wood!! •! ASCII encoding: 8 bits/character (or 7 bits/character)! w! w! w! •! the example string has 32 characters," 4966206120776f6f64…! so we’ll need 256 bits to encode it using ASCII! a! e! a! e! a! e! remove “wade”! remove “wadi”! •! There are only 13 distinct characters in the" d! i! b! d! i! b! i! b! example string, 4 bits/character is enough" to encode the string, for a total of 128 bits! e! i! t! i! t! t! •! Can we do better (use less bits)? How?! symbol! frequency! code! Huffman Codes! Huffman Encoding! I! 1! 11111! The example string:! f! 1! 11110! In the English language, the characters e and t If a woodchuck could a! 1! 11101! occur much more frequently than q and x! chuck wood!! l! 1! 11100! Can we use fewer bits for the former and more Can be encoded using !! 1! 1101! bits for the latter, so that the weighted average the following code (for w! 2! 1100! is less than 5 bits/character?! example)! d! 3! 101! Huffman encoding main ideas:! u! 3! 100! 1.! variable-length encoding: use different number of bits Resulting encoding uses h! 2! 0111! (code length) to represent different symbols! only 111 bits! k! 2! 0110! 2.! entropy encoding: assign smaller code to more •! 111111111000011101…! o! 5! 010! frequently occurring symbols! c! 5! 001! (For binary data, treat each byte as a “character”)! Where do the codes come from?! ‘ ‘! 5! 000! Prefix Codes! How to Construct a Prefix Code?! Since each character is represented by a different Minimize expected number of bits over text! number of bits, we need to know when we have reached the end of a character! If you know the text, you should be able to do this perfectly! There will be no confusion in decoding a string of bits if the bit pattern encoding for one character But top-down allocations are hard to get right! cannot be a prefix of the code for another character! Huffman’s insight is to do this bottom-up, Known as a prefix-free code, or just, prefix code! starting with the two least frequent characters! We have a prefix code if all codes are always located at the leaf nodes of a proper binary trie! I! 11111! f! 11110! Huffman Trie! Huffman Trie Example! a! 11101! l! 11100! Better known as Huffman Tree! If a woodchuck could chuck wood!! !! 1101! w! 1100! Huffman tree construction algorithm:! d! 101! u! 100! •!count the frequency each symbol occurs! 32! 1! h! 0111! •!make each symbol a leaf node, with its frequency as its weight! 0! k! 0110! 13! •!pair up the two least frequently occurring symbols" 1! o! 010! c! 001! (break ties arbitrarily)! 19! 7! 1! 0! 1! ‘ ‘! 000! •!create a subtree of the pair with the root weighing" 0! 0! 9! 4! the sum of its children’s weights! 1! 0! 1! •!repeat until all subtrees have been paired up into a single tree! 10! 4! 6! 3! 2! 2! •!encode each symbol as the path from the root," 0! 1! 0! 0! 1! 0! 1! 0! 1! 0! 1! 0! 1! with a left represented as a 0, and a right a 1! 5’ ‘! 5c! 5o! 2k! 2h! 3u! 3d! 2w! 1!! 1l! 1a! 1f! 1I! Characteristics of Huffman Trees! Encoding Time Complexity! All symbols are leaf nodes by construction,
Load more

Recommended publications
  • An Alternative to Fibonacci Heaps with Worst Case Rather Than Amortized Time Bounds∗
    Relaxed Fibonacci heaps: An alternative to Fibonacci heaps with worst case rather than amortized time bounds¤ Chandrasekhar Boyapati C. Pandu Rangan Department of Computer Science and Engineering Indian Institute of Technology, Madras 600036, India Email: [email protected] November 1995 Abstract We present a new data structure called relaxed Fibonacci heaps for implementing priority queues on a RAM. Relaxed Fibonacci heaps support the operations find minimum, insert, decrease key and meld, each in O(1) worst case time and delete and delete min in O(log n) worst case time. Introduction The implementation of priority queues is a classical problem in data structures. Priority queues find applications in a variety of network problems like single source shortest paths, all pairs shortest paths, minimum spanning tree, weighted bipartite matching etc. [1] [2] [3] [4] [5] In the amortized sense, the best performance is achieved by the well known Fibonacci heaps. They support delete and delete min in amortized O(log n) time and find min, insert, decrease key and meld in amortized constant time. Fast meldable priority queues described in [1] achieve all the above time bounds in worst case rather than amortized time, except for the decrease key operation which takes O(log n) worst case time. On the other hand, relaxed heaps described in [2] achieve in the worst case all the time bounds of the Fi- bonacci heaps except for the meld operation, which takes O(log n) worst case ¤Please see Errata at the end of the paper. 1 time. The problem that was posed in [1] was to consider if it is possible to support both decrease key and meld simultaneously in constant worst case time.
    [Show full text]
  • Data Structures and Algorithms Binary Heaps (S&W 2.4)
    Data structures and algorithms DAT038/TDA417, LP2 2019 Lecture 12, 2019-12-02 Binary heaps (S&W 2.4) Some slides by Sedgewick & Wayne Collections A collection is a data type that stores groups of items. stack Push, Pop linked list, resizing array queue Enqueue, Dequeue linked list, resizing array symbol table Put, Get, Delete BST, hash table, trie, TST set Add, ontains, Delete BST, hash table, trie, TST A priority queue is another kind of collection. “ Show me your code and conceal your data structures, and I shall continue to be mystified. Show me your data structures, and I won't usually need your code; it'll be obvious.” — Fred Brooks 2 Priority queues Collections. Can add and remove items. Stack. Add item; remove the item most recently added. Queue. Add item; remove the item least recently added. Min priority queue. Add item; remove the smallest item. Max priority queue. Add item; remove the largest item. return contents contents operation argument value size (unordered) (ordered) insert P 1 P P insert Q 2 P Q P Q insert E 3 P Q E E P Q remove max Q 2 P E E P insert X 3 P E X E P X insert A 4 P E X A A E P X insert M 5 P E X A M A E M P X remove max X 4 P E M A A E M P insert P 5 P E M A P A E M P P insert L 6 P E M A P L A E L M P P insert E 7 P E M A P L E A E E L M P P remove max P 6 E M A P L E A E E L M P A sequence of operations on a priority queue 3 Priority queue API Requirement.
    [Show full text]
  • Game Trees, Quad Trees and Heaps
    CS 61B Game Trees, Quad Trees and Heaps Fall 2014 1 Heaps of fun R (a) Assume that we have a binary min-heap (smallest value on top) data structue called Heap that stores integers and has properly implemented insert and removeMin methods. Draw the heap and its corresponding array representation after each of the operations below: Heap h = new Heap(5); //Creates a min-heap with 5 as the root 5 5 h.insert(7); 5,7 5 / 7 h.insert(3); 3,7,5 3 /\ 7 5 h.insert(1); 1,3,5,7 1 /\ 3 5 / 7 h.insert(2); 1,2,5,7,3 1 /\ 2 5 /\ 7 3 h.removeMin(); 2,3,5,7 2 /\ 3 5 / 7 CS 61B, Fall 2014, Game Trees, Quad Trees and Heaps 1 h.removeMin(); 3,7,5 3 /\ 7 5 (b) Consider an array based min-heap with N elements. What is the worst case running time of each of the following operations if we ignore resizing? What is the worst case running time if we take into account resizing? What are the advantages of using an array based heap vs. using a BST-based heap? Insert O(log N) Find Min O(1) Remove Min O(log N) Accounting for resizing: Insert O(N) Find Min O(1) Remove Min O(N) Using a BST is not space-efficient. (c) Your friend Alyssa P. Hacker challenges you to quickly implement a max-heap data structure - "Hah! I’ll just use my min-heap implementation as a template", you think to yourself.
    [Show full text]
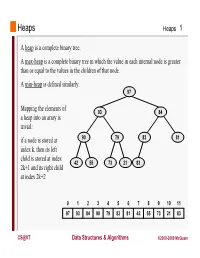
  • Heaps a Heap Is a Complete Binary Tree. a Max-Heap Is A
    Heaps Heaps 1 A heap is a complete binary tree. A max-heap is a complete binary tree in which the value in each internal node is greater than or equal to the values in the children of that node. A min-heap is defined similarly. 97 Mapping the elements of 93 84 a heap into an array is trivial: if a node is stored at 90 79 83 81 index k, then its left child is stored at index 42 55 73 21 83 2k+1 and its right child at index 2k+2 01234567891011 97 93 84 90 79 83 81 42 55 73 21 83 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Building a Heap Heaps 2 The fact that a heap is a complete binary tree allows it to be efficiently represented using a simple array. Given an array of N values, a heap containing those values can be built, in situ, by simply “sifting” each internal node down to its proper location: - start with the last 73 73 internal node * - swap the current 74 81 74 * 93 internal node with its larger child, if 79 90 93 79 90 81 necessary - then follow the swapped node down 73 * 93 - continue until all * internal nodes are 90 93 90 73 done 79 74 81 79 74 81 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Heap Class Interface Heaps 3 We will consider a somewhat minimal maxheap class: public class BinaryHeap<T extends Comparable<? super T>> { private static final int DEFCAP = 10; // default array size private int size; // # elems in array private T [] elems; // array of elems public BinaryHeap() { .
    [Show full text]
  • Priority Queues and Binary Heaps Chapter 6.5
    Priority Queues and Binary Heaps Chapter 6.5 1 Some animals are more equal than others • A queue is a FIFO data structure • the first element in is the first element out • which of course means the last one in is the last one out • But sometimes we want to sort of have a queue but we want to order items according to some characteristic the item has. 107 - Trees 2 Priorities • We call the ordering characteristic the priority. • When we pull something from this “queue” we always get the element with the best priority (sometimes best means lowest). • It is really common in Operating Systems to use priority to schedule when something happens. e.g. • the most important process should run before a process which isn’t so important • data off disk should be retrieved for more important processes first 107 - Trees 3 Priority Queue • A priority queue always produces the element with the best priority when queried. • You can do this in many ways • keep the list sorted • or search the list for the minimum value (if like the textbook - and Unix actually - you take the smallest value to be the best) • You should be able to estimate the Big O values for implementations like this. e.g. O(n) for choosing the minimum value of an unsorted list. • There is a clever data structure which allows all operations on a priority queue to be done in O(log n). 107 - Trees 4 Binary Heap Actually binary min heap • Shape property - a complete binary tree - all levels except the last full.
    [Show full text]
  • Assignment 3: Kdtree ______Due June 4, 11:59 PM
    CS106L Handout #04 Spring 2014 May 15, 2014 Assignment 3: KDTree _________________________________________________________________________________________________________ Due June 4, 11:59 PM Over the past seven weeks, we've explored a wide array of STL container classes. You've seen the linear vector and deque, along with the associative map and set. One property common to all these containers is that they are exact. An element is either in a set or it isn't. A value either ap- pears at a particular position in a vector or it does not. For most applications, this is exactly what we want. However, in some cases we may be interested not in the question “is X in this container,” but rather “what value in the container is X most similar to?” Queries of this sort often arise in data mining, machine learning, and computational geometry. In this assignment, you will implement a special data structure called a kd-tree (short for “k-dimensional tree”) that efficiently supports this operation. At a high level, a kd-tree is a generalization of a binary search tree that stores points in k-dimen- sional space. That is, you could use a kd-tree to store a collection of points in the Cartesian plane, in three-dimensional space, etc. You could also use a kd-tree to store biometric data, for example, by representing the data as an ordered tuple, perhaps (height, weight, blood pressure, cholesterol). However, a kd-tree cannot be used to store collections of other data types, such as strings. Also note that while it's possible to build a kd-tree to hold data of any dimension, all of the data stored in a kd-tree must have the same dimension.
    [Show full text]
  • L11: Quadtrees CSE373, Winter 2020
    L11: Quadtrees CSE373, Winter 2020 Quadtrees CSE 373 Winter 2020 Instructor: Hannah C. Tang Teaching Assistants: Aaron Johnston Ethan Knutson Nathan Lipiarski Amanda Park Farrell Fileas Sam Long Anish Velagapudi Howard Xiao Yifan Bai Brian Chan Jade Watkins Yuma Tou Elena Spasova Lea Quan L11: Quadtrees CSE373, Winter 2020 Announcements ❖ Homework 4: Heap is released and due Wednesday ▪ Hint: you will need an additional data structure to improve the runtime for changePriority(). It does not affect the correctness of your PQ at all. Please use a built-in Java collection instead of implementing your own. ▪ Hint: If you implemented a unittest that tested the exact thing the autograder described, you could run the autograder’s test in the debugger (and also not have to use your tokens). ❖ Please look at posted QuickCheck; we had a few corrections! 2 L11: Quadtrees CSE373, Winter 2020 Lecture Outline ❖ Heaps, cont.: Floyd’s buildHeap ❖ Review: Set/Map data structures and logarithmic runtimes ❖ Multi-dimensional Data ❖ Uniform and Recursive Partitioning ❖ Quadtrees 3 L11: Quadtrees CSE373, Winter 2020 Other Priority Queue Operations ❖ The two “primary” PQ operations are: ▪ removeMax() ▪ add() ❖ However, because PQs are used in so many algorithms there are three common-but-nonstandard operations: ▪ merge(): merge two PQs into a single PQ ▪ buildHeap(): reorder the elements of an array so that its contents can be interpreted as a valid binary heap ▪ changePriority(): change the priority of an item already in the heap 4 L11: Quadtrees CSE373,
    [Show full text]
  • CS210-Data Structures-Module-29-Binary-Heap-II
    Data Structures and Algorithms (CS210A) Lecture 29: • Building a Binary heap on 풏 elements in O(풏) time. • Applications of Binary heap : sorting • Binary trees: beyond searching and sorting 1 Recap from the last lecture 2 A complete binary tree How many leaves are there in a Complete Binary tree of size 풏 ? 풏/ퟐ 3 Building a Binary heap Problem: Given 풏 elements {푥0, …, 푥푛−1}, build a binary heap H storing them. Trivial solution: (Building the Binary heap incrementally) CreateHeap(H); For( 풊 = 0 to 풏 − ퟏ ) What is the time Insert(푥,H); complexity of this algorithm? 4 Building a Binary heap incrementally What useful inference can you draw from Top-down this Theorem ? approach The time complexity for inserting a leaf node = ?O (log 풏 ) # leaf nodes = 풏/ퟐ , Theorem: Time complexity of building a binary heap incrementally is O(풏 log 풏). 5 Building a Binary heap incrementally What useful inference can you draw from Top-down this Theorem ? approach The O(풏) time algorithm must take O(1) time for each of the 풏/ퟐ leaves. 6 Building a Binary heap incrementally Top-down approach 7 Think of alternate approach for building a binary heap In any complete 98 binaryDoes treeit suggest, how a manynew nodes approach satisfy to heapbuild propertybinary heap ? ? 14 33 all leaf 37 11 52 32 nodes 41 21 76 85 17 25 88 29 Bottom-up approach 47 75 9 57 23 heap property: “Every ? node stores value smaller than its children” We just need to ensure this property at each node.
    [Show full text]
  • Rethinking Host Network Stack Architecture Using a Dataflow Modeling Approach
    DISS.ETH NO. 23474 Rethinking host network stack architecture using a dataflow modeling approach A thesis submitted to attain the degree of DOCTOR OF SCIENCES of ETH ZURICH (Dr. sc. ETH Zurich) presented by Pravin Shinde Master of Science, Vrije Universiteit, Amsterdam born on 15.10.1982 citizen of Republic of India accepted on the recommendation of Prof. Dr. Timothy Roscoe, examiner Prof. Dr. Gustavo Alonso, co-examiner Dr. Kornilios Kourtis, co-examiner Dr. Andrew Moore, co-examiner 2016 Abstract As the gap between the speed of networks and processor cores increases, the software alone will not be able to handle all incoming data without additional assistance from the hardware. The network interface controllers (NICs) evolve and add supporting features which could help the system increase its scalability with respect to incoming packets, provide Quality of Service (QoS) guarantees and reduce the CPU load. However, modern operating systems are ill suited to both efficiently exploit and effectively manage the hardware resources of state-of-the-art NICs. The main problem is the layered architecture of the network stack and the rigid interfaces. This dissertation argues that in order to effectively use the diverse and complex NIC hardware features, we need (i) a hardware agnostic representation of the packet processing capabilities of the NICs, and (ii) a flexible interface to share this information with different layers of the network stack. This work presents the Dataflow graph based model to capture both the hardware capabilities for packet processing of the NIC and the state of the network stack, in order to enable automated reasoning about the NIC features in a hardware-agnostic way.
    [Show full text]
  • Priorityqueue
    CSE 373 Java Collection Framework, Part 2: Priority Queue, Map slides created by Marty Stepp http://www.cs.washington.edu/373/ © University of Washington, all rights reserved. 1 Priority queue ADT • priority queue : a collection of ordered elements that provides fast access to the minimum (or maximum) element usually implemented using a tree structure called a heap • priority queue operations: add adds in order; O(log N) worst peek returns minimum value; O(1) always remove removes/returns minimum value; O(log N) worst isEmpty , clear , size , iterator O(1) always 2 Java's PriorityQueue class public class PriorityQueue< E> implements Queue< E> Method/Constructor Description Runtime PriorityQueue< E>() constructs new empty queue O(1) add( E value) adds value in sorted order O(log N ) clear() removes all elements O(1) iterator() returns iterator over elements O(1) peek() returns minimum element O(1) remove() removes/returns min element O(log N ) Queue<String> pq = new PriorityQueue <String>(); pq.add("Stuart"); pq.add("Marty"); ... 3 Priority queue ordering • For a priority queue to work, elements must have an ordering in Java, this means implementing the Comparable interface • many existing types (Integer, String, etc.) already implement this • if you store objects of your own types in a PQ, you must implement it TreeSet and TreeMap also require Comparable types public class Foo implements Comparable<Foo> { … public int compareTo(Foo other) { // Return > 0 if this object is > other // Return < 0 if this object is < other // Return 0 if this object == other } } 4 The Map ADT • map : Holds a set of unique keys and a collection of values , where each key is associated with one value.
    [Show full text]
  • Programmatic Testing of the Standard Template Library Containers
    Programmatic Testing of the Standard Template Library Containers y z Jason McDonald Daniel Ho man Paul Stro op er May 11, 1998 Abstract In 1968, McIlroy prop osed a software industry based on reusable comp onents, serv- ing roughly the same role that chips do in the hardware industry. After 30 years, McIlroy's vision is b ecoming a reality. In particular, the C++ Standard Template Library STL is an ANSI standard and is b eing shipp ed with C++ compilers. While considerable attention has b een given to techniques for developing comp onents, little is known ab out testing these comp onents. This pap er describ es an STL conformance test suite currently under development. Test suites for all of the STL containers have b een written, demonstrating the feasi- bility of thorough and highly automated testing of industrial comp onent libraries. We describ e a ordable test suites that provide go o d co de and b oundary value coverage, including the thousands of cases that naturally o ccur from combinations of b oundary values. We showhowtwo simple oracles can provide fully automated output checking for all the containers. We re ne the traditional categories of black-b ox and white-b ox testing to sp eci cation-based, implementation-based and implementation-dep endent testing, and showhow these three categories highlight the key cost/thoroughness trade- o s. 1 Intro duction Our testing fo cuses on container classes |those providing sets, queues, trees, etc.|rather than on graphical user interface classes. Our approach is based on programmatic testing where the number of inputs is typically very large and b oth the input generation and output checking are under program control.
    [Show full text]
  • CS 270 Algorithms
    CS 270 Algorithms Week 10 Oliver Kullmann Binary heaps Sorting Heapification Building a heap 1 Binary heaps HEAP- SORT Priority 2 Heapification queues QUICK- 3 Building a heap SORT Analysing 4 QUICK- HEAP-SORT SORT 5 Priority queues Tutorial 6 QUICK-SORT 7 Analysing QUICK-SORT 8 Tutorial CS 270 General remarks Algorithms Oliver Kullmann Binary heaps Heapification Building a heap We return to sorting, considering HEAP-SORT and HEAP- QUICK-SORT. SORT Priority queues CLRS Reading from for week 7 QUICK- SORT 1 Chapter 6, Sections 6.1 - 6.5. Analysing 2 QUICK- Chapter 7, Sections 7.1, 7.2. SORT Tutorial CS 270 Discover the properties of binary heaps Algorithms Oliver Running example Kullmann Binary heaps Heapification Building a heap HEAP- SORT Priority queues QUICK- SORT Analysing QUICK- SORT Tutorial CS 270 First property: level-completeness Algorithms Oliver Kullmann Binary heaps In week 7 we have seen binary trees: Heapification Building a 1 We said they should be as “balanced” as possible. heap 2 Perfect are the perfect binary trees. HEAP- SORT 3 Now close to perfect come the level-complete binary Priority trees: queues QUICK- 1 We can partition the nodes of a (binary) tree T into levels, SORT according to their distance from the root. Analysing 2 We have levels 0, 1,..., ht(T ). QUICK- k SORT 3 Level k has from 1 to 2 nodes. Tutorial 4 If all levels k except possibly of level ht(T ) are full (have precisely 2k nodes in them), then we call the tree level-complete. CS 270 Examples Algorithms Oliver The binary tree Kullmann 1 ❚ Binary heaps ❥❥❥❥ ❚❚❚❚ ❥❥❥❥ ❚❚❚❚ ❥❥❥❥ ❚❚❚❚ Heapification 2 ❥ 3 ❖ ❄❄ ❖❖ Building a ⑧⑧ ❄ ⑧⑧ ❖❖ heap ⑧⑧ ❄ ⑧⑧ ❖❖❖ 4 5 6 ❄ 7 ❄ HEAP- ⑧ ❄ ⑧ ❄ SORT ⑧⑧ ❄ ⑧⑧ ❄ Priority 10 13 14 15 queues QUICK- is level-complete (level-sizes are 1, 2, 4, 4), while SORT ❥ 1 ❚❚ Analysing ❥❥❥❥ ❚❚❚❚ QUICK- ❥❥❥ ❚❚❚ SORT ❥❥❥ ❚❚❚❚ 2 ❥❥ 3 ♦♦♦ ❄❄ ⑧ Tutorial ♦♦ ❄❄ ⑧⑧ ♦♦♦ ⑧ 4 ❄ 5 ❄ 6 ❄ ⑧⑧ ❄❄ ⑧ ❄ ⑧ ❄ ⑧⑧ ❄ ⑧⑧ ❄ ⑧⑧ ❄ 8 9 10 11 12 13 is not (level-sizes are 1, 2, 3, 6).
    [Show full text]