An Analysis of XML Compression Efficiency
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

ACS – the Archival Cytometry Standard
http://flowcyt.sf.net/acs/latest.pdf ACS – the Archival Cytometry Standard Archival Cytometry Standard ACS International Society for Advancement of Cytometry Candidate Recommendation DRAFT Document Status The Archival Cytometry Standard (ACS) has undergone several revisions since its initial development in June 2007. The current proposal is an ISAC Candidate Recommendation Draft. It is assumed, however not guaranteed, that significant features and design aspects will remain unchanged for the final version of the Recommendation. This specification has been formally tested to comply with the W3C XML schema version 1.0 specification but no position is taken with respect to whether a particular software implementing this specification performs according to medical or other valid regulations. The work may be used under the terms of the Creative Commons Attribution-ShareAlike 3.0 Unported license. You are free to share (copy, distribute and transmit), and adapt the work under the conditions specified at http://creativecommons.org/licenses/by-sa/3.0/legalcode. Disclaimer of Liability The International Society for Advancement of Cytometry (ISAC) disclaims liability for any injury, harm, or other damage of any nature whatsoever, to persons or property, whether direct, indirect, consequential or compensatory, directly or indirectly resulting from publication, use of, or reliance on this Specification, and users of this Specification, as a condition of use, forever release ISAC from such liability and waive all claims against ISAC that may in any manner arise out of such liability. ISAC further disclaims all warranties, whether express, implied or statutory, and makes no assurances as to the accuracy or completeness of any information published in the Specification. -

Metadefender Core V4.12.2
MetaDefender Core v4.12.2 © 2018 OPSWAT, Inc. All rights reserved. OPSWAT®, MetadefenderTM and the OPSWAT logo are trademarks of OPSWAT, Inc. All other trademarks, trade names, service marks, service names, and images mentioned and/or used herein belong to their respective owners. Table of Contents About This Guide 13 Key Features of Metadefender Core 14 1. Quick Start with Metadefender Core 15 1.1. Installation 15 Operating system invariant initial steps 15 Basic setup 16 1.1.1. Configuration wizard 16 1.2. License Activation 21 1.3. Scan Files with Metadefender Core 21 2. Installing or Upgrading Metadefender Core 22 2.1. Recommended System Requirements 22 System Requirements For Server 22 Browser Requirements for the Metadefender Core Management Console 24 2.2. Installing Metadefender 25 Installation 25 Installation notes 25 2.2.1. Installing Metadefender Core using command line 26 2.2.2. Installing Metadefender Core using the Install Wizard 27 2.3. Upgrading MetaDefender Core 27 Upgrading from MetaDefender Core 3.x 27 Upgrading from MetaDefender Core 4.x 28 2.4. Metadefender Core Licensing 28 2.4.1. Activating Metadefender Licenses 28 2.4.2. Checking Your Metadefender Core License 35 2.5. Performance and Load Estimation 36 What to know before reading the results: Some factors that affect performance 36 How test results are calculated 37 Test Reports 37 Performance Report - Multi-Scanning On Linux 37 Performance Report - Multi-Scanning On Windows 41 2.6. Special installation options 46 Use RAMDISK for the tempdirectory 46 3. Configuring Metadefender Core 50 3.1. Management Console 50 3.2. -

I Introduction
PPM Performance with BWT Complexity: A New Metho d for Lossless Data Compression Michelle E ros California Institute of Technology e [email protected] Abstract This work combines a new fast context-search algorithm with the lossless source co ding mo dels of PPM to achieve a lossless data compression algorithm with the linear context-search complexity and memory of BWT and Ziv-Lemp el co des and the compression p erformance of PPM-based algorithms. Both se- quential and nonsequential enco ding are considered. The prop osed algorithm yields an average rate of 2.27 bits per character bp c on the Calgary corpus, comparing favorably to the 2.33 and 2.34 bp c of PPM5 and PPM and the 2.43 bp c of BW94 but not matching the 2.12 bp c of PPMZ9, which, at the time of this publication, gives the greatest compression of all algorithms rep orted on the Calgary corpus results page. The prop osed algorithm gives an average rate of 2.14 bp c on the Canterbury corpus. The Canterbury corpus web page gives average rates of 1.99 bp c for PPMZ9, 2.11 bp c for PPM5, 2.15 bp c for PPM7, and 2.23 bp c for BZIP2 a BWT-based co de on the same data set. I Intro duction The Burrows Wheeler Transform BWT [1] is a reversible sequence transformation that is b ecoming increasingly p opular for lossless data compression. The BWT rear- ranges the symb ols of a data sequence in order to group together all symb ols that share the same unb ounded history or \context." Intuitively, this op eration is achieved by forming a table in which each row is a distinct cyclic shift of the original data string. -

Dc5m United States Software in English Created at 2016-12-25 16:00
Announcement DC5m United States software in english 1 articles, created at 2016-12-25 16:00 articles set mostly positive rate 10.0 1 3.8 Google’s Brotli Compression Algorithm Lands to Windows Edge Microsoft has announced that its Edge browser has started using Brotli, the compression algorithm that Google open-sourced last year. 2016-12-25 05:00 1KB www.infoq.com Articles DC5m United States software in english 1 articles, created at 2016-12-25 16:00 1 /1 3.8 Google’s Brotli Compression Algorithm Lands to Windows Edge Microsoft has announced that its Edge browser has started using Brotli, the compression algorithm that Google open-sourced last year. Brotli is on by default in the latest Edge build and can be previewed via the Windows Insider Program. It will reach stable status early next year, says Microsoft. Microsoft touts a 20% higher compression ratios over comparable compression algorithms, which would benefit page load times without impacting client-side CPU costs. According to Google, Brotli uses a whole new data format , which makes it incompatible with Deflate but ensures higher compression ratios. In particular, Google says, Brotli is roughly as fast as zlib when decompressing and provides a better compression ratio than LZMA and bzip2 on the Canterbury Corpus. Brotli appears to be especially tuned for the web , that is for offline encoding and online decoding of Web assets, or Android APKs. Google claims a compression ratio improvement of 20–26% over its own Zopfli algorithm, which still provides the best compression ratio of any deflate algorithm. -

Implementing Associative Coder of Buyanovsky (ACB)
Implementing Associative Coder of Buyanovsky (ACB) data compression by Sean Michael Lambert A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science in Computer Science Montana State University © Copyright by Sean Michael Lambert (1999) Abstract: In 1994 George Mechislavovich Buyanovsky published a basic description of a new data compression algorithm he called the “Associative Coder of Buyanovsky,” or ACB. The archive program using this idea, which he released in 1996 and updated in 1997, is still one of the best general compression utilities available. Despite this, the ACB algorithm is still barely understood by data compression experts, primarily because Buyanovsky never published a detailed description of it. ACB is a new idea in data compression, merging concepts from existing statistical and dictionary-based algorithms with entirely original ideas. This document presents several variations of the ACB algorithm and the details required to implement a basic version of ACB. IMPLEMENTING ASSOCIATIVE CODER OF BUYANOVSKY (ACB) DATA COMPRESSION by Sean Michael Lambert A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science in Computer Science MONTANA STATE UNIVERSITY-BOZEMAN Bozeman, Montana April 1999 © COPYRIGHT by Sean Michael Lambert 1999 All Rights Reserved ii APPROVAL of a thesis submitted by Sean Michael Lambert This thesis has been read by each member of the thesis committee and has been found to be satisfactory regarding content, English usage, format, citations, bibliographic style, and consistency, and is ready for submission to the College of Graduate Studies. Brendan Mumey U /l! ^ (Signature) Date Approved for the Department of Computer Science J. -

Desktop Security
JPL Informat'1" I Desktop Security Alan Stepakoff lClS - Desktop Services January 14,2004 JPL lnformatio-” ill*--- Interoperable Computing Environment UWindows 2000, XP +=5500 UMac OS 9, 1O.x += 1800 ULinux Red Hat 8, 9 +=150 orrnatio Desktop Configuration Standard Interoperable Environment MS Word Norton Anti-Virus (F-Prof) PowerPoint Meeting Maker Excel QuickTime player Netscape Real Player Acrobat Reader Timbuktu (VNC) Eudora Stuffit (TAR) SMS or Netoctopus Systems are configured to a standard set of Protective Measures + JPL specific security requirements in-line with NASA regulations + Separate Protective Measure for each OS JPL lnforr_ ” - i_*- User Privileges II Authorization 4 Windows users authorize to Active Directory + Macintosh and Linux users authorize to local system, considering Kerberos Privileges 4 Users are given System Administrative privileges 4 Users are not given System Administrative responsibility 4 Support Contractor has SA privileges and respsonsibility JPL System Management Requirements II Monthly and ad-hoc reporting II New systems delivered secure II Security patches maintained monthly Anti-Virus signature files maintained as needed II Emergency patches within 7 days Quarterlv Service Packs or point releases JPL Information-__1_c System Tools H Periodic ISS scans ITSecure - Custom maintenance utility for Windows II SMS - Windows patch deployment H Netoctopus - Macintosh patch deployment H Norton Anti-Virus Liveupdate Issues ISS scans - may take many scans to capture information w ITSecure needs to be deployed q ua rter I y w SMS + Domain dependant + Too costly to prepare packages w Netoctopus Costly to prepare packages System Management-Future Tools Periodic ISS scans Norton Anti-Virus Liveupdate 4 sus 4 Easy to support 4 Responsibility is transferred to users PatchLink - NASA-wide tool 4 Unobtrusive data gathering and patch delivery + User can control reboot 4 Large patch repository 4 Cross platform 4 Upload data to IT Security Database to close SPL tickets and update configuration information . -
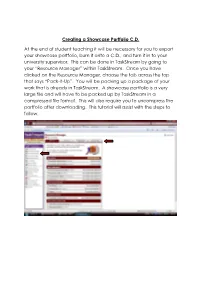
Creating a Showcase Portfolio CD
Creating a Showcase Portfolio C.D. At the end of student teaching it will be necessary for you to export your showcase portfolio, burn it onto a C.D., and turn it in to your university supervisor. This can be done in TaskStream by going to your “Resource Manager” within TaskStream. Once you have clicked on the Resource Manager, choose the tab across the top that says “Pack-It-Up”. You will be packing up a package of your work that is already in TaskStream. A showcase portfolio is a very large file and will have to be packed up by TaskStream in a compressed file format. This will also require you to uncompress the portfolio after downloading. This tutorial will assist with the steps to follow. The next step is to select the work you would like TaskStream to package. This is done by clicking on the tab for selecting work. You will then be asked what type of work you want to package. Your showcase portfolio is a presentation portfolio, so you will click there and click next step. The next step will be to choose the presentation portfolio you want packaged, check the box, and click next step. TaskStream will confirm your selection and then ask you to choose the type of file you need your work to be packaged into. If you are using a computer with a Windows operating system, you will choose a zip file. If you are using a computer with a Macintosh operating system, you will choose a sit file. You will also be asked how you would like TaskStream to notify you that they have completed the task of packing up your work. -

Improving Compression-Ratio in Backup
Institutionen för systemteknik Department of Electrical Engineering Examensarbete Improving compression ratio in backup Examensarbete utfört i Informationskodning/Bildkodning av Mattias Zeidlitz Författare Mattias Zeidlitz LITH-ISY-EX--12/4588--SE Linköping 2012 TEKNISKA HÖGSKOLAN LINKÖPINGS UNIVERSITET Department of Electrical Engineering Linköpings tekniska högskola Linköping University Institutionen för systemteknik S-581 83 Linköping, Sweden 581 83 Linköping Improving compression-ratio in backup ............................................................................ Examensarbete utfört i Informationskodning/Bildkodning vid Linköpings tekniska högskola av Mattias Zeidlitz ............................................................. LITH-ISY-EX--12/4588--SE Presentationsdatum Institution och avdelning 2012-06-13 Institutionen för systemteknik Publiceringsdatum (elektronisk version) Department of Electrical Engineering Datum då du ämnar publicera exjobbet Språk Typ av publikation ISBN (licentiatavhandling) Svenska Licentiatavhandling ISRN LITH-ISY-EX--12/4588--SE x Annat (ange nedan) x Examensarbete Serietitel (licentiatavhandling) C-uppsats D-uppsats Engelska Rapport Serienummer/ISSN (licentiatavhandling) Antal sidor Annat (ange nedan) 58 URL för elektronisk version http://www.ep.liu.se Publikationens titel Improving compression ratio in backup Författare Mattias Zeidlitz Sammanfattning Denna rapport beskriver ett examensarbete genomfört på Degoo Backup AB i Stockholm under våren 2012. Syftet var att designa en kompressionssvit -

Frequently Asked Questions from Researchers and Downloaders
Frequently Asked Questions from Researchers and Downloaders Table of contents 1. What format are the images and packages?..................................................................... 2 1.1. What format is each package of images and documents?...........................................2 1.2. My system does not understand bzip2 or tar files - where can I get a tool to decompress them?........................................................................................................................................2 1.3. Is the package available as a zip file instead?.............................................................2 1.4. What file format are the images?................................................................................2 1.5. What file format are the report documents?................................................................2 1.6. Is there a DICOMDIR?...............................................................................................2 2. Can the images be viewed on line or accessed individually?...........................................3 2.1. Can the images be viewed on line?............................................................................ 3 2.2. Can the images be accessed or downloaded individually?..........................................3 2.3. Are the images available in alternative formats?........................................................ 3 3. How can I download the files?.........................................................................................3 -

Benefits of Hardware Data Compression in Storage Networks Gerry Simmons, Comtech AHA Tony Summers, Comtech AHA SNIA Legal Notice
Benefits of Hardware Data Compression in Storage Networks Gerry Simmons, Comtech AHA Tony Summers, Comtech AHA SNIA Legal Notice The material contained in this tutorial is copyrighted by the SNIA. Member companies and individuals may use this material in presentations and literature under the following conditions: Any slide or slides used must be reproduced without modification The SNIA must be acknowledged as source of any material used in the body of any document containing material from these presentations. This presentation is a project of the SNIA Education Committee. Oct 17, 2007 Benefits of Hardware Data Compression in Storage Networks 2 © 2007 Storage Networking Industry Association. All Rights Reserved. Abstract Benefits of Hardware Data Compression in Storage Networks This tutorial explains the benefits and algorithmic details of lossless data compression in Storage Networks, and focuses especially on data de-duplication. The material presents a brief history and background of Data Compression - a primer on the different data compression algorithms in use today. This primer includes performance data on the specific compression algorithms, as well as performance on different data types. Participants will come away with a good understanding of where to place compression in the data path, and the benefits to be gained by such placement. The tutorial will discuss technological advances in compression and how they affect system level solutions. Oct 17, 2007 Benefits of Hardware Data Compression in Storage Networks 3 © 2007 Storage Networking Industry Association. All Rights Reserved. Agenda Introduction and Background Lossless Compression Algorithms System Implementations Technology Advances and Compression Hardware Power Conservation and Efficiency Conclusion Oct 17, 2007 Benefits of Hardware Data Compression in Storage Networks 4 © 2007 Storage Networking Industry Association. -
![Archive and Compressed [Edit]](https://docslib.b-cdn.net/cover/8796/archive-and-compressed-edit-1288796.webp)
Archive and Compressed [Edit]
Archive and compressed [edit] Main article: List of archive formats • .?Q? – files compressed by the SQ program • 7z – 7-Zip compressed file • AAC – Advanced Audio Coding • ace – ACE compressed file • ALZ – ALZip compressed file • APK – Applications installable on Android • AT3 – Sony's UMD Data compression • .bke – BackupEarth.com Data compression • ARC • ARJ – ARJ compressed file • BA – Scifer Archive (.ba), Scifer External Archive Type • big – Special file compression format used by Electronic Arts for compressing the data for many of EA's games • BIK (.bik) – Bink Video file. A video compression system developed by RAD Game Tools • BKF (.bkf) – Microsoft backup created by NTBACKUP.EXE • bzip2 – (.bz2) • bld - Skyscraper Simulator Building • c4 – JEDMICS image files, a DOD system • cab – Microsoft Cabinet • cals – JEDMICS image files, a DOD system • cpt/sea – Compact Pro (Macintosh) • DAA – Closed-format, Windows-only compressed disk image • deb – Debian Linux install package • DMG – an Apple compressed/encrypted format • DDZ – a file which can only be used by the "daydreamer engine" created by "fever-dreamer", a program similar to RAGS, it's mainly used to make somewhat short games. • DPE – Package of AVE documents made with Aquafadas digital publishing tools. • EEA – An encrypted CAB, ostensibly for protecting email attachments • .egg – Alzip Egg Edition compressed file • EGT (.egt) – EGT Universal Document also used to create compressed cabinet files replaces .ecab • ECAB (.ECAB, .ezip) – EGT Compressed Folder used in advanced systems to compress entire system folders, replaced by EGT Universal Document • ESS (.ess) – EGT SmartSense File, detects files compressed using the EGT compression system. • GHO (.gho, .ghs) – Norton Ghost • gzip (.gz) – Compressed file • IPG (.ipg) – Format in which Apple Inc. -

The Deep Learning Solutions on Lossless Compression Methods for Alleviating Data Load on Iot Nodes in Smart Cities
sensors Article The Deep Learning Solutions on Lossless Compression Methods for Alleviating Data Load on IoT Nodes in Smart Cities Ammar Nasif *, Zulaiha Ali Othman and Nor Samsiah Sani Center for Artificial Intelligence Technology (CAIT), Faculty of Information Science & Technology, University Kebangsaan Malaysia, Bangi 43600, Malaysia; [email protected] (Z.A.O.); [email protected] (N.S.S.) * Correspondence: [email protected] Abstract: Networking is crucial for smart city projects nowadays, as it offers an environment where people and things are connected. This paper presents a chronology of factors on the development of smart cities, including IoT technologies as network infrastructure. Increasing IoT nodes leads to increasing data flow, which is a potential source of failure for IoT networks. The biggest challenge of IoT networks is that the IoT may have insufficient memory to handle all transaction data within the IoT network. We aim in this paper to propose a potential compression method for reducing IoT network data traffic. Therefore, we investigate various lossless compression algorithms, such as entropy or dictionary-based algorithms, and general compression methods to determine which algorithm or method adheres to the IoT specifications. Furthermore, this study conducts compression experiments using entropy (Huffman, Adaptive Huffman) and Dictionary (LZ77, LZ78) as well as five different types of datasets of the IoT data traffic. Though the above algorithms can alleviate the IoT data traffic, adaptive Huffman gave the best compression algorithm. Therefore, in this paper, Citation: Nasif, A.; Othman, Z.A.; we aim to propose a conceptual compression method for IoT data traffic by improving an adaptive Sani, N.S.