A CCD Search for Variable Stars of Spectral Type B in the Northern
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Optical/IR Studies of Be Stars in NGC 6834 with Emphasis on Two Specific
RAA 2014 Vol. 14 No. 9, 1173–1192 doi: 10.1088/1674–4527/14/9/008 Research in http://www.raa-journal.org http://www.iop.org/journals/raa Astronomy and Astrophysics Optical/IR studies of Be stars in NGC 6834 with emphasis on two specific stars Blesson Mathew1,4, Watson P. Varricatt2, Annapurni Subramaniam3, N. M. Ashok4 and D. P. K. Banerjee4 1 Centre for Astrophysics & Supercomputing, Swinburne University, Hawthorn VIC 3122, Australia; [email protected] 2 Joint Astronomy Centre, 660 N. Aohoku Pl., Hilo, HI 96720, USA 3 Indian Institute of Astrophysics, Bangalore - 560 034, India 4 Astronomy and Astrophysics Division, Physical Research Laboratory, Navrangapura, Ahmedabad - 380 009, Gujarat, India Received 2014 February 12; accepted 2014 March 24 Abstract We present optical and infrared photometric and spectroscopic studies of two Be stars in the 70–80-Myr-old open cluster NGC 6834. NGC 6834(1) has been reported as a binary from speckle interferometric studies whereas NGC 6834(2) may possibly be a γ Cas-like variable. Infrared photometry and spectroscopy from the United Kingdom Infrared Telescope (UKIRT), and optical data from various facil- ities are combined with archival data to understand the nature of these candidates. High signal-to-noise near-IR spectra obtained from UKIRT have enabled us to study the optical depth effects in the hydrogen emission lines of these stars. We have ex- plored the spectral classification scheme based on the intensity of emission lines in the H and K bands and contrasted it with the conventional classification based on the intensity of hydrogen and helium absorption lines. -

Astronomy 2008 Index
Astronomy Magazine Article Title Index 10 rising stars of astronomy, 8:60–8:63 1.5 million galaxies revealed, 3:41–3:43 185 million years before the dinosaurs’ demise, did an asteroid nearly end life on Earth?, 4:34–4:39 A Aligned aurorae, 8:27 All about the Veil Nebula, 6:56–6:61 Amateur astronomy’s greatest generation, 8:68–8:71 Amateurs see fireballs from U.S. satellite kill, 7:24 Another Earth, 6:13 Another super-Earth discovered, 9:21 Antares gang, The, 7:18 Antimatter traced, 5:23 Are big-planet systems uncommon?, 10:23 Are super-sized Earths the new frontier?, 11:26–11:31 Are these space rocks from Mercury?, 11:32–11:37 Are we done yet?, 4:14 Are we looking for life in the right places?, 7:28–7:33 Ask the aliens, 3:12 Asteroid sleuths find the dino killer, 1:20 Astro-humiliation, 10:14 Astroimaging over ancient Greece, 12:64–12:69 Astronaut rescue rocket revs up, 11:22 Astronomers spy a giant particle accelerator in the sky, 5:21 Astronomers unearth a star’s death secrets, 10:18 Astronomers witness alien star flip-out, 6:27 Astronomy magazine’s first 35 years, 8:supplement Astronomy’s guide to Go-to telescopes, 10:supplement Auroral storm trigger confirmed, 11:18 B Backstage at Astronomy, 8:76–8:82 Basking in the Sun, 5:16 Biggest planet’s 5 deepest mysteries, The, 1:38–1:43 Binary pulsar test affirms relativity, 10:21 Binocular Telescope snaps first image, 6:21 Black hole sets a record, 2:20 Black holes wind up galaxy arms, 9:19 Brightest starburst galaxy discovered, 12:23 C Calling all space probes, 10:64–10:65 Calling on Cassiopeia, 11:76 Canada to launch new asteroid hunter, 11:19 Canada’s handy robot, 1:24 Cannibal next door, The, 3:38 Capture images of our local star, 4:66–4:67 Cassini confirms Titan lakes, 12:27 Cassini scopes Saturn’s two-toned moon, 1:25 Cassini “tastes” Enceladus’ plumes, 7:26 Cepheus’ fall delights, 10:85 Choose the dome that’s right for you, 5:70–5:71 Clearing the air about seeing vs. -

На Правах Рукописи Удк 524.3, 524.4, 524.6 Глушкова Елена
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени М.В. ЛОМОНОСОВА ГОСУДАРСТВЕННЫЙ АСТРОНОМИЧЕСКИЙ ИНСТИТУТ имени П.К. ШТЕРНБЕРГА На правах рукописи УДК 524.3, 524.4, 524.6 Глушкова Елена Вячеславовна КОМПЛЕКСНОЕ ИССЛЕДОВАНИЕ РАССЕЯННЫХ ЗВЁЗДНЫХ СКОПЛЕНИЙ ГАЛАКТИКИ Специальность 01.03.02 ± астрофизика и звёздная астрономия Диссертация на соискание ученой степени доктора физико-математических наук Москва ± 2014 1 Оглавление Введение ...................................................................................................................................................4 Глава 1. Собственные движения и лучевые скорости РЗС..................................................................19 1.1. Абсолютные собственные движения..........................................................................................19 1.1.1 Абсолютизация собственных движений звёзд в 21 рассеянном скоплении.....................20 1.1.2 Оценка ошибок каталога 4М...............................................................................................27 1.1.3 Оценка параметров кривой вращения по собственным движениям 21 РЗС....................28 1.1.4 Абсолютные собственные движения 181 молодого скопления.........................................28 1.1.5 Кривая вращения подсистемы молодых рассеянных скоплений......................................37 1.1.6 Каталог абсолютных собственных движений РЗС.............................................................38 1.1.7 Членство звёзд в скоплениях...............................................................................................39 -

Survey of Emission Line Stars in Young Open Clusters
SurveySurvey ofof emissionemission lineline starsstars inin youngyoung openopen clustersclusters AnnapurniAnnapurni SubramaniamSubramaniam Collaborators: Blesson Mathew & B.C. Bhatt EmissionEmission lineline stars:stars: whatwhat areare they?they? These stars show H-alpha emission lines in their spectra – indication of circum-stellar material. Two classes: (1) remnant of the accretion disk – pre-Main sequence stars – Herbig Ae/Be stars (2) Classical Be stars – material thrown out of the star forming a disk. These stars are well studied in the field – not in clusters - uncertainty in estimating their distance, interstellar reddening, age, mass and evolutionary state. ClusterCluster stars:stars: advantageadvantage TheseThese starsstars locatedlocated inin clustersclusters helphelp toto estimateestimate theirtheir propertiesproperties accuratelyaccurately –– distance,distance, reddening,reddening, massmass (spectral(spectral type)type) andand age.age. ToTo studystudy thethe emissionemission phenomenonphenomenon asas aa functionfunction ofof stellarstellar propertiesproperties –– possiblepossible inin thethe casecase ofof clustersclusters stars.stars. PropertiesProperties ofof thethe circumcircum--stellarstellar diskdisk cancan bebe studiedstudied asas aa functionfunction ofof massmass andand age.age. LargeLarge numbernumber ofof starsstars cancan bebe identifiedidentified toto havehave aa largelarge sample,sample, willwill helphelp toto studystudy andand classifyclassify themthem intointo variousvarious groups.groups. DataData Aim: -

2005-6 Eye on The
THE TEXAS STAR PARTY 2005 TELESCOPE OBSERVING CLUB BY JOHN WAGONER TEXAS ASTRONOMICAL SOCIETY OF DALLAS RULES AND REGULATIONS Welcome to the Texas Star Party's Telescope Observing Club. The purpose of this club is not to test your observing skills by throwing the toughest objects at you that are hard to see under any conditions, but to give you an opportunity to observe 25 showcase objects under the ideal conditions of these pristine West Texas skies, thus displaying them to their best advantage. This year we are going to get a little wild and wooly. If you thought you can observe all night and sleep all day, you are wrong. This year we will be observing 24/7. That’s right, Clayton Jeter of the Houston Astronomical Society has provided us with a daytime observing program. It is called the Bright Sky Observing Program and details are below. The regular observing program is “Eye in the Sky”. This program is a mixture of all the things that you have requested in an observing program. Brad Schaefer of Austin, Tx. wanted Naked Eye objects while Barbara Wilson of Houston, Tx. suggested Reflection Nebula. Someone else wanted Dark Nebula while still another idea was to bring back those pesky planetaries. To this end, I have listed ten Naked Eye objects. They are marked with an “NE” next to the catalog number. If for some reason your tired old eyes just can’t pull them out, then you may use binoculars. Also, if you have trouble with any object on the list, make an effort and then go to the next one. -

Optical/IR Studies of Be Stars in NGC 6834 with Emphasis on Two Specific
RAA 2014 Vol. 14 No. 9, 1173–1192 doi: 10.1088/1674–4527/14/9/008 Research in http://www.raa-journal.org http://www.iop.org/journals/raa Astronomy and Astrophysics Optical/IR studies of Be stars in NGC 6834 with emphasis on two specific stars Blesson Mathew1;4, Watson P. Varricatt2, Annapurni Subramaniam3, N. M. Ashok4 and D. P. K. Banerjee4 1 Centre for Astrophysics & Supercomputing, Swinburne University, Hawthorn VIC 3122, Australia; [email protected] 2 Joint Astronomy Centre, 660 N. Aohoku Pl., Hilo, HI 96720, USA 3 Indian Institute of Astrophysics, Bangalore - 560 034, India 4 Astronomy and Astrophysics Division, Physical Research Laboratory, Navrangapura, Ahmedabad - 380 009, Gujarat, India Received 2014 February 12; accepted 2014 March 24 Abstract We present optical and infrared photometric and spectroscopic studies of two Be stars in the 70–80-Myr-old open cluster NGC 6834. NGC 6834(1) has been reported as a binary from speckle interferometric studies whereas NGC 6834(2) may possibly be a γ Cas-like variable. Infrared photometry and spectroscopy from the United Kingdom Infrared Telescope (UKIRT), and optical data from various facil- ities are combined with archival data to understand the nature of these candidates. High signal-to-noise near-IR spectra obtained from UKIRT have enabled us to study the optical depth effects in the hydrogen emission lines of these stars. We have ex- plored the spectral classification scheme based on the intensity of emission lines in the H and K bands and contrasted it with the conventional classification based on the intensity of hydrogen and helium absorption lines. -

A CCD Search for Variable Stars of Spectral Type B in the Northern Hemisphere Open Clusters
ACTA ASTRONOMICA Vol. 61 (2011) pp. 247–273 A CCD Search for Variable Stars of Spectral Type B in the Northern Hemisphere Open Clusters. VIII. NGC 6834 M. Jerzykiewicz1 , G.Kopacki1 , A. Pigulski1 , Z. Kołaczkowski1 and S.-L. Kim2 1 Astronomical Institute, University of Wrocław, ul. Kopernika 11, 51-622 Wrocław, Poland e-mail: (mjerz,kopacki,pigulski,kolaczkowski)@astro.uni.wroc.pl 2 Korea Astronomy and Space Science Institute, Daejeon 305-348, Korea, e-mail: [email protected] Received July 16, 2011 ABSTRACT We present results of a CCD variability search in the field of the young open cluster NGC6834. We discover 15 stars to be variable in light. The brightest, a multiperiodic γ Doradus-type variable is a foreground star. The eight fainter ones, including a γ Cassiopeiae-type variable, two λ Eridani-type variables, an ellipsoidal variable, an EB-type eclipsing binary, and three variable stars we could not classify, all have E(B−V) within proper range, thus fulfilling the necessary condition to be members. One of the three unclassified variables may be a non-member on account of its large angular distance from the center of the cluster. Four of the six faintest variable stars, which include two eclipsing binaries and two very red stars showing year-to-year variations, are certain non-members. One of the remaining two faintest variable stars, an EA-type eclipsing binary may be a member, while the faintest one, a W Ursae Majoris-type variable, is probably a non-member. For 6937 stars we provide the V magnitudes and V − IC color indices on the standard system. -
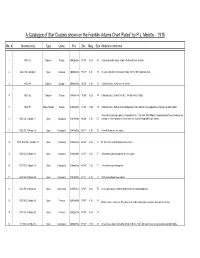
A Catalogue of Star Clusters Shown on the Franklin-Adams Chart Plates” by P.J
A Catalogue of Star Clusters shown on the Franklin-Adams Chart Plates” by P.J. Melotte – 1915 Mel. # Alternative(s) Type Const. R.A. Dec. Mag. Size Melotte's comments 1 NGC 104 Globular Tucana 00h24m04s -72°05' 4.00 50' A typical globular cluster. Bright. Well condensed at centre. 2 NGC 188, Collinder 6 Open Cepheus 00h47m28s +85°15' 9.30 17' "A somewhat ill-defined cluster mostly 14th to 16th magnitude stars. 3 NGC 288 Globular Sculptor 00h52m45s -26°35' 8.10 13' Globular cluster, rather loose at centre. 4 NGC 362 Globular Tucana 01h03m14s -70°50' 6.80 14' Globular cluster. Similar to N.G.C. 104 but smaller. Bright. 5 NGC 371 Diffuse Nebula Tucana 01h03m30s -72°03' 13.80 7.5' Globular cluster. Falls in smaller Magellanic cloud, and has every appearance of being a globular cluster. A few stars clustering together. Resembles N.G.C. 582, 645, 659. Difficult to decide whether these should not be 6 NGC 436, Collinder 11 Open Cassiopeia 01h15m58s +58°48' 9.30 5.0' classed II. All the clusters here resemble one another though differing in extent. 7 NGC 457, Collinder 12 Open Cassiopeia 01h19m35s +58°17' 5.10 20' A small cluster in a rich region. 8 M103, NGC 581, Collinder 14 Open Cassiopeia 01h33m23s +60°39' 6.90 5' M. 103. A few stars forming a loose cluster. 9 NGC 654, Collinder 18 Open Cassiopeia 01h44m00s +61°53' 8.20 5' A few stars clustered together in a rich region. 10 NGC 659, Collinder 19 Open Cassiopeia 01h44m24s +60°40' 7.20 5' A few stars clustered together. -

Sh 2 - 308 in Canis Major
Wolf-Rayet Nebula Reiner Vogel 2012 Sh 2 - 308 in Canis Major 60x60, blue RGB Dean Salman OIII other name RA dec dia. ' F S B Sh 2-308 06 54 08.9 -23 56 31 35 3 3 2 Distance: 575 pc, Size: 5.9 pc, Source: 2003MNRAS.346.1143B This ring nebula surrounds the Wolf-Rayet star WR 6. Observing notes: 22" f/4.5 01/2011. Fantastic WR bubble, responds extremely well to OIII filter. Shell is most obvious as a crescent NW of o1 CMa, becoming fainter at NW. Brighter patch again at N to NE. At 80x under excellent conditions, the shell can be further followed from this N part down the E side back to o1 CMa, forming a closed bubble around EZ CMa. Only with 7mm exit pupil, the center appears filled and somewhat lighter than the outside of the bubble. This is not visible with 5.5mm exit pupil. Sirius 7h30m 7h00m 6h30m i Bochum 4 Murzim n3 n1 NGC 2 n2 p 15 17 -20°00' M 41 12 Canis Major x2 x1 o2 o1 29 Cr 121 t -25°00' NGC26 2354 27 Wezen w Markab s Adara Aludra Furud -30°00' 10 -22°00' 7h05m 7h00m 6h55m 6h50m 6h45m Canis Major -23°00' o2 -24°00' o1 Cr 121 -25°00' NGC 2359 in Canis Major 60x60, red narrowband, Dean Salman other name RA dec dia. ' F S B Sh 2-298 NGC2359 = Thor's Helmet 07 18 38.0 -13 11 55 22 3 3 3 Distance: 5000 pc, Size: 32.0 pc, Source: 2001AJ....121.2664C Nicknamed Thor's Helmet, this nebula (also called NGC 2359) is a wind blown bubble ionized by the Wolf-Rayet star WR 7 (HD 56925). -

Touring the Trumpler Classes
Touring the Trumpler Classes By Richard Harshaw Saguaro Astronomy Club Phoenix, Arizona Robert Trumpler (1886-1956) was a Swiss astronomer (he became a naturalized American citizen in 1921) who contributed greatly to our understanding of open star clusters in his 1930 paper, “Preliminary results on the distances, dimensions and space distribution of open star clusters.i” In writing his paper, he created a cluster classification scheme that is still in use today. Trumpler’s system makes use of three codes to describe a cluster (later there were additions of other codes, but that need not concern us here). The first code was a Roman numeral from I to IV to denote how detached the cluster was from the background/foreground stars. A cluster of type I is well- detached—it almost seems isolated in the sky, with very little clutter around it distract the eye. A type IV is virtually indistinguishable from the background. The second code was a numeral from 1 to 3 to denote the general spread in magnitudes. A rating of 1 means there is little difference in the magnitudes of the members—they all appear to be nearly the same magnitude (plus or minus a magnitude or two). A type 3 has a very wide range of magnitudes, often with one very bright member dominating a dim background of lacey haze. The third code was a richness code, using r, m, and p (for “rich,” “medium and “poor”). A rich cluster had over 100 stars in it; a medium cluster between 50 and 100; and a poor one less than 50. -

The COLOUR of CREATION Observing and Astrophotography Targets “At a Glance” Guide
The COLOUR of CREATION observing and astrophotography targets “at a glance” guide. (Naked eye, binoculars, small and “monster” scopes) Dear fellow amateur astronomer. Please note - this is a work in progress – compiled from several sources - and undoubtedly WILL contain inaccuracies. It would therefor be HIGHLY appreciated if readers would be so kind as to forward ANY corrections and/ or additions (as the document is still obviously incomplete) to: [email protected]. The document will be updated/ revised/ expanded* on a regular basis, replacing the existing document on the ASSA Pretoria website, as well as on the website: coloursofcreation.co.za . This is by no means intended to be a complete nor an exhaustive listing, but rather an “at a glance guide” (2nd column), that will hopefully assist in choosing or eliminating certain objects in a specific constellation for further research, to determine suitability for observation or astrophotography. There is NO copy right - download at will. Warm regards. JohanM. *Edition 1: June 2016 (“Pre-Karoo Star Party version”). “To me, one of the wonders and lures of astronomy is observing a galaxy… realizing you are detecting ancient photons, emitted by billions of stars, reduced to a magnitude below naked eye detection…lying at a distance beyond comprehension...” ASSA 100. (Auke Slotegraaf). Messier objects. Apparent size: degrees, arc minutes, arc seconds. Interesting info. AKA’s. Emphasis, correction. Coordinates, location. Stars, star groups, etc. Variable stars. Double stars. (Only a small number included. “Colourful Ds. descriptions” taken from the book by Sissy Haas). Carbon star. C Asterisma. (Including many “Streicher” objects, taken from Asterism. -

August 2019 BRAS Newsletter
A Monthly Meeting August 12th at 7PM at HRPO (Monthly meetings are on 2nd Mondays, Highland Road Park Observatory). Program: John Nagle will share his experiences at the Texas Star Party last May, includes video. What's In This Issue? President’s Message Secretary's Summary Outreach Report Astrophotography Group Asteroid and Comet News Light Pollution Committee Report Globe at Night Member’s Corner – John Nagle at the Texas Star Party Messages from the HRPO Science Academy Friday Night Lecture Series Solar Viewing Perseid Meteor Shower Celestial Fantasia Plus Night Observing Notes: Cygnus – The Swan & Mythology Like this newsletter? See PAST ISSUES online back to 2009 Visit us on Facebook – Baton Rouge Astronomical Society Newsletter of the Baton Rouge Astronomical Society Page 2 August 2019 © 2019 President’s Message July 20, 2019, marked the 50th anniversary of the Apollo 11 Moon Landing. I was able to attend the Astronomical League’s 50th anniversary celebration of the moon landing, held in Titusville, Florida from July 25th through July 29th, 2019, and their cruise to the Bahamas on the Mariner Of The Seas. It was great fun. We went to the Kennedy Space Center to meet Astronaut Al Worden. We also saw the July 25 SpaceX launch from the parking lot of a Cracker Barrel restaurant near the hotel. Food and talk were great. AL’s Apollo 11 cruise to the Bahamas on Royal Caribbean’s “Mariner Of The Seas” ALCON 2018 and 2019 was so much fun I believe we should host one. I am setting up the "ALCON 2022 Bid Preparation and Planning Committee" to look into it.