Polynomial Identity Testing
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Lesson 6: Trigonometric Identities
1. Introduction An identity is an equality relationship between two mathematical expressions. For example, in basic algebra students are expected to master various algbriac factoring identities such as a2 − b2 =(a − b)(a + b)or a3 + b3 =(a + b)(a2 − ab + b2): Identities such as these are used to simplifly algebriac expressions and to solve alge- a3 + b3 briac equations. For example, using the third identity above, the expression a + b simpliflies to a2 − ab + b2: The first identiy verifies that the equation (a2 − b2)=0is true precisely when a = b: The formulas or trigonometric identities introduced in this lesson constitute an integral part of the study and applications of trigonometry. Such identities can be used to simplifly complicated trigonometric expressions. This lesson contains several examples and exercises to demonstrate this type of procedure. Trigonometric identities can also used solve trigonometric equations. Equations of this type are introduced in this lesson and examined in more detail in Lesson 7. For student’s convenience, the identities presented in this lesson are sumarized in Appendix A 2. The Elementary Identities Let (x; y) be the point on the unit circle centered at (0; 0) that determines the angle t rad : Recall that the definitions of the trigonometric functions for this angle are sin t = y tan t = y sec t = 1 x y : cos t = x cot t = x csc t = 1 y x These definitions readily establish the first of the elementary or fundamental identities given in the table below. For obvious reasons these are often referred to as the reciprocal and quotient identities. -

CHAPTER 8. COMPLEX NUMBERS Why Do We Need Complex Numbers? First of All, a Simple Algebraic Equation Like X2 = −1 May Not Have
CHAPTER 8. COMPLEX NUMBERS Why do we need complex numbers? First of all, a simple algebraic equation like x2 = 1 may not have a real solution. − Introducing complex numbers validates the so called fundamental theorem of algebra: every polynomial with a positive degree has a root. However, the usefulness of complex numbers is much beyond such simple applications. Nowadays, complex numbers and complex functions have been developed into a rich theory called complex analysis and be- come a power tool for answering many extremely difficult questions in mathematics and theoretical physics, and also finds its usefulness in many areas of engineering and com- munication technology. For example, a famous result called the prime number theorem, which was conjectured by Gauss in 1849, and defied efforts of many great mathematicians, was finally proven by Hadamard and de la Vall´ee Poussin in 1896 by using the complex theory developed at that time. A widely quoted statement by Jacques Hadamard says: “The shortest path between two truths in the real domain passes through the complex domain”. The basic idea for complex numbers is to introduce a symbol i, called the imaginary unit, which satisfies i2 = 1. − In doing so, x2 = 1 turns out to have a solution, namely x = i; (actually, there − is another solution, namely x = i). We remark that, sometimes in the mathematical − literature, for convenience or merely following tradition, an incorrect expression with correct understanding is used, such as writing √ 1 for i so that we can reserve the − letter i for other purposes. But we try to avoid incorrect usage as much as possible. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

Section 5.4 the Other Trigonometric Functions 333
Section 5.4 The Other Trigonometric Functions 333 Section 5.4 The Other Trigonometric Functions In the previous section, we defined the sine and cosine functions as ratios of the sides of a right triangle in a circle. Since the triangle has 3 sides there are 6 possible combinations of ratios. While the sine and cosine are the two prominent ratios that can be formed, there are four others, and together they define the 6 trigonometric functions. Tangent, Secant, Cosecant, and Cotangent Functions For the point (x, y) on a circle of radius r at an angle of θ , we can define four additional important functions as the ratios of the (x, y) sides of the corresponding triangle: y r The tangent function: tan(θ ) = y x θ r The secant function: sec(θ ) = x x r The cosecant function: csc(θ ) = y x The cotangent function: cot(θ ) = y Geometrically, notice that the definition of tangent corresponds with the slope of the line segment between the origin (0, 0) and the point (x, y). This relationship can be very helpful in thinking about tangent values. You may also notice that the ratios defining the secant, cosecant, and cotangent are the reciprocals of the ratios defining the cosine, sine, and tangent functions, respectively. Additionally, notice that using our results from the last section, y r sin(θ ) sin(θ ) tan(θ ) = = = x r cos(θ ) cos(θ ) Applying this concept to the other trig functions we can state the other reciprocal identities. Identities The other four trigonometric functions can be related back to the sine and cosine functions using these basic relationships: sin(θ ) 1 1 1 cos(θ ) tan(θ ) = sec(θ ) = csc(θ ) = cot(θ ) = = cos(θ ) cos(θ ) sin(θ ) tan(θθ ) sin( ) 334 Chapter 5 These relationships are called identities. -

Complex Numbers Euler's Identity
2.003 Fall 2003 Complex Exponentials Complex Numbers ² Complex numbers have both real and imaginary components. A complex number r may be expressed in Cartesian or Polar forms: r = a + jb (cartesian) = jrjeÁ (polar) The following relationships convert from cartesian to polar forms: p Magnitude jrj = a2 + b2 ( ¡1 b tan a a > 0 Angle Á = ¡1 b tan a § ¼ a < 0 ² Complex numbers can be plotted on the complex plane in either Cartesian or Polar forms Fig.1. Figure 1: Complex plane plots: Cartesian and Polar forms Euler's Identity Euler's Identity states that ejÁ = cos Á + j sin Á 1 2.003 Fall 2003 Complex Exponentials This can be shown by taking the series expansion of sin, cos, and e. Á3 Á5 Á7 sin Á = Á ¡ + ¡ + ::: 3! 5! 7! Á2 Á4 Á6 cos Á = 1 ¡ + ¡ + ::: 2! 4! 6! Á2 Á3 Á4 Á5 ejÁ = 1 + jÁ ¡ ¡ j + + j + ::: 2! 3! 4! 5! Combining (Á)2 Á3 Á4 Á5 cos Á + j sin Á = 1 + jÁ ¡ ¡ j + + j + ::: 2! 3! 4! 5! = ejÁ Complex Exponentials ² Consider the case where Á becomes a function of time increasing at a constant rate ! Á(t) = !t: then r(t) becomes r(t) = ej!t Plotting r(t) on the complex plane traces out a circle with a constant radius = 1 (Fig. 2 ). Plotting the real and imaginary components of r(t) vs time (Fig. 3 ), we see that the real component is Refr(t)g = cos !t while the imaginary component is Imfr(t)g = sin !t. ² Consider the variable r(t) which is de¯ned as follows: r(t) = est where s is a complex number s = σ + j! 2 2.003 Fall 2003 Complex Exponentials t Figure 2: Complex plane plots: r(t) = ej!t t 0 t Re[ r(t) ]=cos t 0 t Im[ r(t) ]=sin t Figure 3: Real and imaginary components of r(t) vs time ² What path does r(t) trace out in the complex plane ? Consider r(t) = est = e(σ+j!)t = eσt ¢ ej!t One can look at this as a time varying magnitude (eσt) multiplying a point rotating on the unit circle at frequency ! via the function ej!t. -

Intervening in Student Identity in Mathematics Education: an Attempt to Increase Motivation to Learn Mathematics
INTERNATIONAL ELECTRONIC JOURNAL OF MATHEMATICS EDUCATION e-ISSN: 1306-3030. 2020, Vol. 15, No. 3, em0597 OPEN ACCESS https://doi.org/10.29333/iejme/8326 Intervening in Student Identity in Mathematics Education: An Attempt to Increase Motivation to Learn Mathematics Kayla Heffernan 1*, Steven Peterson 2, Avi Kaplan 3, Kristie J. Newton 4 1 Department of Mathematics, University of Pittsburgh at Greensburg, 150 Finoli Drive, Greensburg, PA 15601, USA 2 Haverford High School, 200 Mill Road, Havertown, PA 19083, USA 3 Department of Psychological Studies in Education, Temple University, 1301 Cecil B. Moore Avenue, Philadelphia, PA 19122, USA 4 Department of Teaching and Learning, Temple University, 1301 Cecil B. Moore Avenue, Philadelphia, PA 19122, USA * CORRESPONDENCE: [email protected] ABSTRACT Students’ relationships with mathematics continuously remain problematic, and researchers have begun to look at this issue through the lens of identity. In this article, the researchers discuss identity in education research, specifically in mathematics classrooms, and break down the various perspective on identity. A review of recent literature that explicitly invokes identity as a construct in intervention studies is presented, with a devoted attention to research on identity interventions in mathematics classrooms categorized based on the various perspectives of identity. Across perspectives, the review demonstrates that mathematics identities motivate action and that mathematics educators can influence students’ mathematical identities. The purpose of this paper is to help readers, researchers, and educators understand the various perspectives on identity, understand that identity can be influenced, and learn how researchers and educators have thus far, and continue to study identity interventions in mathematics classrooms. -

On Orders of Elements in Quasigroups
BULETINUL ACADEMIEI DE S¸TIINT¸E A REPUBLICII MOLDOVA. MATEMATICA Number 2(45), 2004, Pages 49–54 ISSN 1024–7696 On orders of elements in quasigroups Victor Shcherbacov Abstract. We study the connection between the existence in a quasigroupof(m, n)- elements for some natural numbers m, n and properties of this quasigroup. The special attention is given for case of (m, n)-linear quasigroups and (m, n)-T-quasigroups. Mathematics subject classification: 20N05. Keywords and phrases: Quasigroup, medial quasigroup, T-quasigroup, order of an element of a quasigroup. 1 Introduction We shall use basic terms and concepts from books [1, 2, 11]. We recall that a binary groupoid (Q, A) with n-ary operation A such that in the equality A(x1,x2)= x3 knowledge of any two elements of x1,x2,x3 the uniquely specifies the remaining one is called a binary quasigroup [3]. It is possible to define a binary quasigroup also as follows. Definition 1. A binary groupoid (Q, ◦) is called a quasigroup if for any element (a, b) of the set Q2 there exist unique solutions x,y ∈ Q to the equations x ◦ a = b and a ◦ y = b [1]. An element f(b) of a quasigroup (Q, ·) is called a left local identity element of an element b ∈ Q, if f(b) · b = b. An element e(b) of a quasigroup (Q, ·) is called a right local identity element of an element b ∈ Q, if b · e(b)= b. The fact that an element e is a left (right) identity element of a quasigroup (Q, ·) means that e = f(x) for all x ∈ Q (respectively, e = e(x) for all x ∈ Q). -

Euler's Formula: 1 Powers of E: First Pass
Euler’s Formula: The purpose of these notes is to explain Euler’s famous formula eiθ = cos(θ)+ i sin(θ). (1) 1 Powers of e: First Pass Euler’s equation is complicated because it involves raising a number to an imaginary power. Let’s build up to this slowly. Integer Powers: It’s pretty clear that e2 = e e and e3 = e e e, × × × and so on. For any positive integer p, we have ep = e ... e, a total of p times. For negative integers, the definition is also pretty× clear.× For instance e−2 =1/(e e) and e−3 =1/(e e e). And so on. × × × Fractional Powers: How would you define e2/3. This really means the cube root of e e. So e2/3 is the number y such that y y y = e e. Using this system, it× is pretty clear that you can make good sense× × of ep/q×where p/q is any positive fraction. You can make sense of negative fractions using the formula e−p/q =1/ep/q. Real Powers: If a is a positive real number, then you could define ea to pn/qn be the limit of expressions of the form e , where pn/qn is a sequence of rational numbers converging to a. To give an example of what I’m talking about, let a = √2. 17/12 is close to √2 and e17/12 =4.1233529... • 41/29 is closer to √2 and e41/29 =4.111521... • 577/408 is closer to √2 and e577/408 =4.113259 • 1393/985 is closer to √2 and e1393/985 =4.1132488. -

Math 311 - Introduction to Proof and Abstract Mathematics Group Assignment # 15 Name: Due: at the End of Class on Tuesday, March 26Th
Math 311 - Introduction to Proof and Abstract Mathematics Group Assignment # 15 Name: Due: At the end of class on Tuesday, March 26th More on Functions: Definition 5.1.7: Let A, B, C, and D be sets. Let f : A B and g : C D be functions. Then f = g if: → → A = C and B = D • For all x A, f(x)= g(x). • ∈ Intuitively speaking, this definition tells us that a function is determined by its underlying correspondence, not its specific formula or rule. Another way to think of this is that a function is determined by the set of points that occur on its graph. 1. Give a specific example of two functions that are defined by different rules (or formulas) but that are equal as functions. 2. Consider the functions f(x)= x and g(x)= √x2. Find: (a) A domain for which these functions are equal. (b) A domain for which these functions are not equal. Definition 5.1.9 Let X be a set. The identity function on X is the function IX : X X defined by, for all x X, → ∈ IX (x)= x. 3. Let f(x)= x cos(2πx). Prove that f(x) is the identity function when X = Z but not when X = R. Definition 5.1.10 Let n Z with n 0, and let a0,a1, ,an R such that an = 0. The function p : R R is a ∈ ≥ ··· ∈ 6 n n−1 → polynomial of degree n with real coefficients a0,a1, ,an if for all x R, p(x)= anx +an−1x + +a1x+a0. -

Theoretical Probability and Statistics
Theoretical Probability and Statistics Charles J. Geyer Copyright 1998, 1999, 2000, 2001, 2008 by Charles J. Geyer September 5, 2008 Contents 1 Finite Probability Models 1 1.1 Probability Mass Functions . 1 1.2 Events and Measures . 5 1.3 Random Variables and Expectation . 6 A Greek Letters 9 B Sets and Functions 11 B.1 Sets . 11 B.2 Intervals . 12 B.3 Functions . 12 C Summary of Brand-Name Distributions 14 C.1 The Discrete Uniform Distribution . 14 C.2 The Bernoulli Distribution . 14 i Chapter 1 Finite Probability Models The fundamental idea in probability theory is a probability model, also called a probability distribution. Probability models can be specified in several differ- ent ways • probability mass function (PMF), • probability density function (PDF), • distribution function (DF), • probability measure, and • function mapping from one probability model to another. We will meet probability mass functions and probability measures in this chap- ter, and will meet others later. The terms “probability model” and “probability distribution” don’t indicate how the model is specified, just that it is specified somehow. 1.1 Probability Mass Functions A probability mass function (PMF) is a function pr Ω −−−−→ R which satisfies the following conditions: its values are nonnegative pr(ω) ≥ 0, ω ∈ Ω (1.1a) and sum to one X pr(ω) = 1. (1.1b) ω∈Ω The domain Ω of the PMF is called the sample space of the probability model. The sample space is required to be nonempty in order that (1.1b) make sense. 1 CHAPTER 1. FINITE PROBABILITY MODELS 2 In this chapter we require all sample spaces to be finite sets. -

MAT 240 - Algebra I Fields Definition
MAT 240 - Algebra I Fields Definition. A field is a set F , containing at least two elements, on which two operations + and · (called addition and multiplication, respectively) are defined so that for each pair of elements x, y in F there are unique elements x + y and x · y (often written xy) in F for which the following conditions hold for all elements x, y, z in F : (i) x + y = y + x (commutativity of addition) (ii) (x + y) + z = x + (y + z) (associativity of addition) (iii) There is an element 0 ∈ F , called zero, such that x+0 = x. (existence of an additive identity) (iv) For each x, there is an element −x ∈ F such that x+(−x) = 0. (existence of additive inverses) (v) xy = yx (commutativity of multiplication) (vi) (x · y) · z = x · (y · z) (associativity of multiplication) (vii) (x + y) · z = x · z + y · z and x · (y + z) = x · y + x · z (distributivity) (viii) There is an element 1 ∈ F , such that 1 6= 0 and x·1 = x. (existence of a multiplicative identity) (ix) If x 6= 0, then there is an element x−1 ∈ F such that x · x−1 = 1. (existence of multiplicative inverses) Remark: The axioms (F1)–(F-5) listed in the appendix to Friedberg, Insel and Spence are the same as those above, but are listed in a different way. Axiom (F1) is (i) and (v), (F2) is (ii) and (vi), (F3) is (iii) and (vii), (F4) is (iv) and (ix), and (F5) is (vii). Proposition. Let F be a field. -
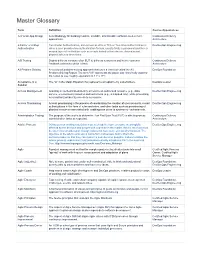
Master Glossary
Master Glossary Term Definition Course Appearances 12-Factor App Design A methodology for building modern, scalable, maintainable software-as-a-service Continuous Delivery applications. Architecture 2-Factor or 2-Step Two-Factor Authentication, also known as 2FA or TFA or Two-Step Authentication is DevSecOps Engineering Authentication when a user provides two authentication factors; usually firstly a password and then a second layer of verification such as a code texted to their device, shared secret, physical token or biometrics. A/B Testing Deploy different versions of an EUT to different customers and let the customer Continuous Delivery feedback determine which is best. Architecture A3 Problem Solving A structured problem-solving approach that uses a lean tool called the A3 DevOps Foundation Problem-Solving Report. The term "A3" represents the paper size historically used for the report (a size roughly equivalent to 11" x 17"). Acceptance of a The "A" in the Magic Equation that represents acceptance by stakeholders. DevOps Leader Solution Access Management Granting an authenticated identity access to an authorized resource (e.g., data, DevSecOps Engineering service, environment) based on defined criteria (e.g., a mapped role), while preventing an unauthorized identity access to a resource. Access Provisioning Access provisioning is the process of coordinating the creation of user accounts, e-mail DevSecOps Engineering authorizations in the form of rules and roles, and other tasks such as provisioning of physical resources associated with enabling new users to systems or environments. Administration Testing The purpose of the test is to determine if an End User Test (EUT) is able to process Continuous Delivery administration tasks as expected.