Generating Programs by Reflection*
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Attachment A
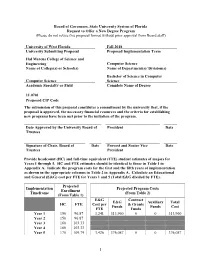
Board of Governors, State University System of Florida Request to Offer a New Degree Program (Please do not revise this proposal format without prior approval from Board staff) University of West Florida Fall 2018 University Submitting Proposal Proposed Implementation Term Hal Marcus College of Science and Engineering Computer Science Name of College(s) or School(s) Name of Department(s)/ Division(s) Bachelor of Science in Computer Computer Science Science Academic Specialty or Field Complete Name of Degree 11.0701 Proposed CIP Code The submission of this proposal constitutes a commitment by the university that, if the proposal is approved, the necessary financial resources and the criteria for establishing new programs have been met prior to the initiation of the program. Date Approved by the University Board of President Date Trustees Signature of Chair, Board of Date Provost and Senior Vice Date Trustees President Provide headcount (HC) and full-time equivalent (FTE) student estimates of majors for Years 1 through 5. HC and FTE estimates should be identical to those in Table 1 in Appendix A. Indicate the program costs for the first and the fifth years of implementation as shown in the appropriate columns in Table 2 in Appendix A. Calculate an Educational and General (E&G) cost per FTE for Years 1 and 5 (Total E&G divided by FTE). Projected Implementation Projected Program Costs Enrollment Timeframe (From Table 2) (From Table 1) E&G Contract E&G Auxiliary Total HC FTE Cost per & Grants Funds Funds Cost FTE Funds Year 1 150 96.87 3,241 313,960 0 0 313,960 Year 2 150 96.87 Year 3 160 103.33 Year 4 160 103.33 Year 5 170 109.79 3,426 376,087 0 0 376,087 1 Note: This outline and the questions pertaining to each section must be reproduced within the body of the proposal to ensure that all sections have been satisfactorily addressed. -

The Circle Meta-Model
Document:P2062R0 Revises: (original) Date: 01-11-2020 Audience: SG7 Authors: Wyatt Childers ([email protected]) Andrew Sutton ([email protected]) Faisal Vali ([email protected]) Daveed Vandevoorde ([email protected]) The Circle Meta-model Introduction During the November 2019 meeting in Belfast, some of the SG7 participants enthusiastically mentioned Circle1 as providing a more intuitive compile-time programming model and suggested that SG7 investigate overhauling the de-facto SG7 approach (P1240+P17332) to follow Circle's general approach (to reflection and metaprogramming). This paper describes a framework for understanding metaprogramming systems and provides a high-level overview of some of Circle's main characteristics, contrasting them to P1240's approach augmented with an injection mechanism along the lines of P1717. While we appreciate some of Circle’s powerful capabilities, we also raise some concerns with its underlying model and provide arguments in support of P1240’s choices as being a more suitable fit for C++’s evolution. The Dimensions of Reflective Programming In P0633, we identified three “dimensions” of compile-time reflective metaprogramming: 1. Control: How are compile-time computations effected/interpreted? What are metaprograms? 2. Reflection: How are source constructs are made available as data for use in metaprograms? 3. Synthesis: How can “code” be generated from a programmatic representation? 1 https://www.circle-lang.org/ Circle is an impressive project: Sean Baxter developed a brand new C++17-like front end on top of LLVM, incorporating a variety of new compile-time capabilities that align closely with SG7's goals. For Sean’s motivations, see https://github.com/seanbaxter/circle/blob/master/examples/README.md#why-i-wrote-circle. -

Comparative Studies of Programming Languages; Course Lecture Notes
Comparative Studies of Programming Languages, COMP6411 Lecture Notes, Revision 1.9 Joey Paquet Serguei A. Mokhov (Eds.) August 5, 2010 arXiv:1007.2123v6 [cs.PL] 4 Aug 2010 2 Preface Lecture notes for the Comparative Studies of Programming Languages course, COMP6411, taught at the Department of Computer Science and Software Engineering, Faculty of Engineering and Computer Science, Concordia University, Montreal, QC, Canada. These notes include a compiled book of primarily related articles from the Wikipedia, the Free Encyclopedia [24], as well as Comparative Programming Languages book [7] and other resources, including our own. The original notes were compiled by Dr. Paquet [14] 3 4 Contents 1 Brief History and Genealogy of Programming Languages 7 1.1 Introduction . 7 1.1.1 Subreferences . 7 1.2 History . 7 1.2.1 Pre-computer era . 7 1.2.2 Subreferences . 8 1.2.3 Early computer era . 8 1.2.4 Subreferences . 8 1.2.5 Modern/Structured programming languages . 9 1.3 References . 19 2 Programming Paradigms 21 2.1 Introduction . 21 2.2 History . 21 2.2.1 Low-level: binary, assembly . 21 2.2.2 Procedural programming . 22 2.2.3 Object-oriented programming . 23 2.2.4 Declarative programming . 27 3 Program Evaluation 33 3.1 Program analysis and translation phases . 33 3.1.1 Front end . 33 3.1.2 Back end . 34 3.2 Compilation vs. interpretation . 34 3.2.1 Compilation . 34 3.2.2 Interpretation . 36 3.2.3 Subreferences . 37 3.3 Type System . 38 3.3.1 Type checking . 38 3.4 Memory management . -

Sub-Method Structural and Behavioral Reflection Marcus Denker
Sub-method Structural and Behavioral Reflection Marcus Denker To cite this version: Marcus Denker. Sub-method Structural and Behavioral Reflection. Computer Science [cs]. Universität Bern, 2008. English. tel-00555937 HAL Id: tel-00555937 https://tel.archives-ouvertes.fr/tel-00555937 Submitted on 14 Jan 2011 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Sub-method Structural and Behavioral Reflection Inauguraldissertation der Philosophisch-naturwissenschaftlichen Fakultät der Universität Bern vorgelegt von Marcus Denker von Deutschland Leiter der Arbeit: Prof. Dr. O. Nierstrasz Institut für Informatik und angewandte Mathematik Von der Philosophisch-naturwissenschaftlichen Fakultät angenommen. Bern, 26.05.2008 Der Dekan: Prof. Dr. P. Messerli This dissertation is available as a free download from http://scg.unibe.ch Copyright © 2008 Marcus Denker. The contents of this dissertation are protected under Creative Commons Attribution-ShareAlike 3.0 Unported license. You are free: to Share — to copy, distribute and transmit the work to Remix — to adapt the work Under the following conditions: Attribution. You must attribute the work in the manner specified by the author or licensor (but not in any way that suggests that they endorse you or your use of the work). -

Directly Reflective Meta-Programming
Directly Reflective Meta-Programming ∗ Aaron Stump Computer Science and Engineering Washington University in St. Louis St. Louis, Missouri, USA [email protected] Abstract Existing meta-programming languages operate on encodings of pro- grams as data. This paper presents a new meta-programming language, based on an untyped lambda calculus, in which structurally reflective pro- gramming is supported directly, without any encoding. The language fea- tures call-by-value and call-by-name lambda abstractions, as well as novel reflective features enabling the intensional manipulation of arbitrary pro- gram terms. The language is scope safe, in the sense that variables can neither be captured nor escape their scopes. The expressiveness of the language is demonstrated by showing how to implement quotation and evaluation operations, as proposed by Wand. The language's utility for meta-programming is further demonstrated through additional represen- tative examples. A prototype implementation is described and evaluated. Keywords: lambda calculus, reflection, meta-programming, Church en- coding, Mogensen-Scott encoding, Wand-style fexprs, alpha equivalence, language implementation. 1 Introduction This paper presents a new meta-programming language called Archon, in which programs can operate directly on other programs as data. Existing meta- programming languages suffer from defects such as encoding programs at too low a level of abstraction, or in a way that bloats the encoded program terms. Other issues include the possibility for variables either to be captured or escape their static scopes. Archon rectifies these defects by trading the complexity of the reflective encoding for additional programming constructs. We adopt ∗This work is supported by funding from the U.S. -
![[Lirmm-00862477, V1] Bridging the Gap Between Component-Based Design and Implementation with a Reflective Programming Language](https://docslib.b-cdn.net/cover/8348/lirmm-00862477-v1-bridging-the-gap-between-component-based-design-and-implementation-with-a-reflective-programming-language-1008348.webp)
[Lirmm-00862477, V1] Bridging the Gap Between Component-Based Design and Implementation with a Reflective Programming Language
Design and Implementation of a reflective Component-based programming and modeling language Bridging the Gap between Component-based Design and Implementation with a Reflective Programming Language Petr Spacek Christophe Dony Luc Fabresse Chouki Tibermacine Universite´ Lille Nord de France LIRMM, CNRS and Montpellier II University Ecole des Mines de Douai 161, rue Ada 941 rue Charles Bourseul 34392 Montpellier Cedex 5 France 59508 DOUAI Cedex France spacek,dony,tibermacin @lirmm.fr [email protected] { } Abstract General Terms Languages, Reflection, Metamodeling Component-based Software Engineering studies the design, Keywords Component, Programming, Modeling, Archi- development and maintenance of software constructed upon tecture, Reflection, Reflexive, Meta-model, Constraints, sets of connected components. Existing component-based Transformations models are frequently transformed into non-component- based programs, most of the time object-oriented, for run- time execution and then many component-related concepts, 1. Introduction e.g. explicit architecture, vanish at the implementation stage. Research works on component-based software engineering The main reason why is that with objects the component- (CBSE) have brought many advances on how to achieve related concepts are treated implicitly and therefore the orig- complex software development by reusing and assembling inal intentions and qualities of the component-based design components. The current trend is to explicitly express ar- are hidden. This paper presents a reflective component-based chitectures of software solutions, to reason about them, to programming and modeling language, which proposes the verify them and to transform them. However it appears following original contributions: 1) Components are seen that component-orientation has been more studied at de- as objects in which requirements, architecture descriptions, sign stage, with modeling languages and ADLs [10, 16, 22] connection points, etc. -

Open Programming Language Interpreters
Open Programming Language Interpreters Walter Cazzolaa and Albert Shaqiria a Università degli Studi di Milano, Italy Abstract Context: This paper presents the concept of open programming language interpreters, a model to support them and a prototype implementation in the Neverlang framework for modular development of programming languages. Inquiry: We address the problem of dynamic interpreter adaptation to tailor the interpreter’s behaviour on the task to be solved and to introduce new features to fulfil unforeseen requirements. Many languages provide a meta-object protocol (MOP) that to some degree supports reflection. However, MOPs are typically language-specific, their reflective functionality is often restricted, and the adaptation and application logic are often mixed which hardens the understanding and maintenance of the source code. Our system overcomes these limitations. Approach: We designed a model and implemented a prototype system to support open programming language interpreters. The implementation is integrated in the Neverlang framework which now exposes the structure, behaviour and the runtime state of any Neverlang-based interpreter with the ability to modify it. Knowledge: Our system provides a complete control over interpreter’s structure, behaviour and its runtime state. The approach is applicable to every Neverlang-based interpreter. Adaptation code can potentially be reused across different language implementations. Grounding: Having a prototype implementation we focused on feasibility evaluation. The paper shows that our approach well addresses problems commonly found in the research literature. We have a demon- strative video and examples that illustrate our approach on dynamic software adaptation, aspect-oriented programming, debugging and context-aware interpreters. Importance: Our paper presents the first reflective approach targeting a general framework for language development. -

1. with Examples of Different Programming Languages Show How Programming Languages Are Organized Along the Given Rubrics: I
AGBOOLA ABIOLA CSC302 17/SCI01/007 COMPUTER SCIENCE ASSIGNMENT 1. With examples of different programming languages show how programming languages are organized along the given rubrics: i. Unstructured, structured, modular, object oriented, aspect oriented, activity oriented and event oriented programming requirement. ii. Based on domain requirements. iii. Based on requirements i and ii above. 2. Give brief preview of the evolution of programming languages in a chronological order. 3. Vividly distinguish between modular programming paradigm and object oriented programming paradigm. Answer 1i). UNSTRUCTURED LANGUAGE DEVELOPER DATE Assembly Language 1949 FORTRAN John Backus 1957 COBOL CODASYL, ANSI, ISO 1959 JOSS Cliff Shaw, RAND 1963 BASIC John G. Kemeny, Thomas E. Kurtz 1964 TELCOMP BBN 1965 MUMPS Neil Pappalardo 1966 FOCAL Richard Merrill, DEC 1968 STRUCTURED LANGUAGE DEVELOPER DATE ALGOL 58 Friedrich L. Bauer, and co. 1958 ALGOL 60 Backus, Bauer and co. 1960 ABC CWI 1980 Ada United States Department of Defence 1980 Accent R NIS 1980 Action! Optimized Systems Software 1983 Alef Phil Winterbottom 1992 DASL Sun Micro-systems Laboratories 1999-2003 MODULAR LANGUAGE DEVELOPER DATE ALGOL W Niklaus Wirth, Tony Hoare 1966 APL Larry Breed, Dick Lathwell and co. 1966 ALGOL 68 A. Van Wijngaarden and co. 1968 AMOS BASIC FranÇois Lionet anConstantin Stiropoulos 1990 Alice ML Saarland University 2000 Agda Ulf Norell;Catarina coquand(1.0) 2007 Arc Paul Graham, Robert Morris and co. 2008 Bosque Mark Marron 2019 OBJECT-ORIENTED LANGUAGE DEVELOPER DATE C* Thinking Machine 1987 Actor Charles Duff 1988 Aldor Thomas J. Watson Research Center 1990 Amiga E Wouter van Oortmerssen 1993 Action Script Macromedia 1998 BeanShell JCP 1999 AngelScript Andreas Jönsson 2003 Boo Rodrigo B. -

Programação Reflexiva Sobre O Protocolo De Meta-Objetos Guaraná
Programação Reflexiva sobre o Protocolo de Meta-Objetos Guaraná Rodrigo Dias Arruda Senra Dissertação de Mestrado Instituto de Computação Universidade Estadual de Campinas Programação Reflexiva sobre o Protocolo de Meta-Objetos Guaraná Rodrigo Dias Arruda Senra 17 de dezembro de 2001 Banca Examinadora: • Prof. Dr. Luiz Eduardo Buzato IC-UNICAMP (Orientador) • Prof~ Dr~ Ana Maria de Alencar Price II-DFRGS • Profª Drª Cecília Mary Fisher Rubira IC-DNICAMP • Prof. Dr. Hans Kurt Edmund Liesenberg (Suplente) IC-UNICAMP ii UN!CAMP FICHA CATALOGRÁFICA ELABORADA PELA BffiLIOTECA DO IMECC DA UNICAMP Senra, Rodrígo Dias Arruda Se99p Programação reflexiva sobre o protocolo de meta-<Jbjetos Guaraná I Rodrígo Dias Arruda Senra- Campinas, [S.P. :s.n.], 2001. Orientador : Luiz Eduardo Buzato Dissertação (mestrado)- Universidade Estadual de Campinas, Instituto de Computação. I. Linguagem de programação (Computadores). 2. Framework (Programa de computador). 3. Programação orientada a objetos (Computador). L Buzato, Luiz Eduardo. li. Universidade Estadual de Campinas. Instituto de Computação. Ili. Título. i ia TERMO DE APROVAÇÃO Te se defendida e aprovada em 17 de dezembro de 2001 , pela Banca Examinadora composta pelos Professores Doutores: Pí'6M. Dra. Ana Maria ~lencar Pri~e UFRGS Prof. Dr. Luiz Edu IC- UNICAMP MP iii Programação Reflexiva sobre o Protocolo de Meta-Objetos Guaraná Este exemplar corresponde à redação final da Dissertação devidamente corrigida e defendida por Rodrigo Dias Arruda Senra e aprovada pela Banca Examinadora. Campinas, 17 de dezembro de 2001. Prof. Dr. Luiz IC-U:'-JICAM Dissertação apresentada ao Instituto de Com putação, Cl\"ICAMP, como requisito parcial para a obtenção do título de :V1estre em Ciência da Computação. -

Reflective Designs
Electronic Notes in Theoretical Computer Science 127 (2005) 55–58 www.elsevier.com/locate/entcs Reflective Designs — An Overview Robert Hirschfeld1 DoCoMo Communications Laboratories Europe Munich, Germany Ralf L¨ammel2 Vrije Universiteit & Centrum voor Wiskunde en Informatica Amsterdam, The Netherlands Abstract We render runtime system adaptations by design-level concepts such that running systems can be adapted and examined at a higher level of abstraction. The overall idea is to express design decisions as applications of design operators to be carried out at runtime. Design operators can implement design patterns for use at runtime. Applications of design operators are made explicit as design elements in the running system such that they can be traced, reconfigured, and made undone. Our approach enables Reflective Designs: on one side, design operators employ reflection to perform runtime adaptations; on the other side, design elements provide an additional reflection protocol to examine and configure performed adaptations. Our approach helps understanding the development and the maintenance of the class of software systems that cannot tolerate downtime or frequent shutdown-revise-startup cycles. We have accumulated a class library for programming with Reflective Designs in Squeak/Smalltalk. This library employs reflection and dynamic aspect-oriented programming. We have also implemented tool support for navigating in a system that is adapted continuously at runtime. Note: This extended abstract summarises our full paper [7]. Keywords: Reflective Designs, Runtime Adaptation, Design Elements, Design Operators, Design Patterns, Reflection, Method-Call Interception, Meta-Programming, Aspect-Oriented Programming, Dynamic Weaving, Dynamic Composition, AspectS, Squeak, Smalltalk, Metaobject Protocol 1 Email: [email protected] 2 Email: [email protected] 1571-0661/$ – see front matter © 2005 Published by Elsevier B.V. -

Static Reflection
N3996- Static reflection Document number: N3996 Date: 2014-05-26 Project: Programming Language C++, SG7, Reflection Reply-to: Mat´uˇsChochl´ık([email protected]) Static reflection How to read this document The first two sections are devoted to the introduction to reflection and reflective programming, they contain some motivational examples and some experiences with usage of a library-based reflection utility. These can be skipped if you are knowledgeable about reflection. Section3 contains the rationale for the design decisions. The most important part is the technical specification in section4, the impact on the standard is discussed in section5, the issues that need to be resolved are listed in section7, and section6 mentions some implementation hints. Contents 1. Introduction4 2. Motivation and Scope6 2.1. Usefullness of reflection............................6 2.2. Motivational examples.............................7 2.2.1. Factory generator............................7 3. Design Decisions 11 3.1. Desired features................................. 11 3.2. Layered approach and extensibility...................... 11 3.2.1. Basic metaobjects........................... 12 3.2.2. Mirror.................................. 12 3.2.3. Puddle.................................. 12 3.2.4. Rubber................................. 13 3.2.5. Lagoon................................. 13 3.3. Class generators................................ 14 3.4. Compile-time vs. Run-time reflection..................... 16 4. Technical Specifications 16 4.1. Metaobject Concepts............................. -

Comparative Studies of 10 Programming Languages Within 10 Diverse Criteria Revision 1.0
Comparative Studies of 10 Programming Languages within 10 Diverse Criteria Revision 1.0 Rana Naim∗ Mohammad Fahim Nizam† Concordia University Montreal, Concordia University Montreal, Quebec, Canada Quebec, Canada [email protected] [email protected] Sheetal Hanamasagar‡ Jalal Noureddine§ Concordia University Montreal, Concordia University Montreal, Quebec, Canada Quebec, Canada [email protected] [email protected] Marinela Miladinova¶ Concordia University Montreal, Quebec, Canada [email protected] Abstract This is a survey on the programming languages: C++, JavaScript, AspectJ, C#, Haskell, Java, PHP, Scala, Scheme, and BPEL. Our survey work involves a comparative study of these ten programming languages with respect to the following criteria: secure programming practices, web application development, web service composition, OOP-based abstractions, reflection, aspect orientation, functional programming, declarative programming, batch scripting, and UI prototyping. We study these languages in the context of the above mentioned criteria and the level of support they provide for each one of them. Keywords: programming languages, programming paradigms, language features, language design and implementation 1 Introduction Choosing the best language that would satisfy all requirements for the given problem domain can be a difficult task. Some languages are better suited for specific applications than others. In order to select the proper one for the specific problem domain, one has to know what features it provides to support the requirements. Different languages support different paradigms, provide different abstractions, and have different levels of expressive power. Some are better suited to express algorithms and others are targeting the non-technical users. The question is then what is the best tool for a particular problem.