DOCSLIB.ORG

Finding the Expansion Rate and the Age of the Universe Learning Goals 1

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Finding the Expansion Rate and the Age of the Universe Learning Goals 1 Finding the Expansion Rate and the Age of the Universe Learning Goals 1. Determine a value for the Hubble constant through analysis of measurements of the angular sizes and redshifts of galaxies. 2. Estimate the corresponding age of the universe and compare it with the age of the Sun and the Milky Way. 3. Explain why Hubble’s law implies that the universe is expanding. 4. Summarize how our view of the universe has changed as the value of the Hubble constant has improved. Galaxy Types: Sizes – Dwarf and Giant • An elliptical or irregular galaxy can be a dwarf galaxy or a giant galaxy. All spirals are giant; that is, all are approximately the same actual size. Standard Ruler • Standard Candle: An object where we are quite confident we know its actual luminosity. • Standard Ruler: An object where we are quite confident we know its actual size. • Assume all spiral galaxies that look similar are very close in actual physical size, no matter where located. • Must first KNOW actual size by using the KNOWN distance to a nearby spiral galaxy - Andromeda galaxy. Variable Stars: Cepheid Variables Vs. RR Lyrae Variables These pulsating variable stars are extremely important for determining distances. Specifically, they have a relationship between their pulsation period and luminosity. Cepheid variables: High-mass stars becoming supergiants. • Periods from 1 to 100 days. More luminous stars have longer periods. RR Lyrae variables: Low-mass stars on the horizontal branch. Less luminous than Cepheid variables. Standard Candles 7 Andromeda Galaxy: Measure �, know D from period- luminosity measurements of Cepheid variable stars, solve for s. Distant Galaxy: Measure �, know s from standard ruler assumption, get D from small angle formula. Standard Ruler - Why is assumption important? � How would we know if the difference in � angular sizes was due to distances or to the galaxies actually being different actual size? 120 ACTIVITY 26 ● Finding the Expansion Rate and the Age of the Universe TABLE 26.1 ConfirmationContinued. for galaxies being spiral VELOCITY DISTANCE GALAXY IMAGE GALAXY SPECTRUM GALAXY ID REDSHIFT (km/s) (Mpc) NGC 1832 0.00646 1,937 32 NGC 2276 0.00806 2,417 26 NGC 2775 0.00451 1,353 20 NGC 2903 0.00186 556 10 NGC 3034 0.00073 219 12 NGC 3147 0.00935 2,804 22 ACTIVITY 26 ● Finding the Expansion Rate and the Age of the Universe 121 TABLE 26.1 ConfirmationContinued. for galaxies being spiral VELOCITY DISTANCE GALAXY IMAGE GALAXY SPECTRUM GALAXY ID REDSHIFT (km/s) (Mpc) NGC 3227 0.00365 1,093 17 NGC 3368 0.00301 903 15 NGC 3623 0.00254 762 8 NGC 3627 0.00234 703 9 NGC 4775 0.00624 1,572 24 NGC 5248 0.00384 1,152 13 (continued) Standard ruler gives estimate of distances ➔ x-axis Examination of the redshifts of the spectra gives us the recessional velocities ➔ y-axis Expanding Universe: Doppler Shift Measurements • Recall: Redshifted spectral lines = movement away; blue shifted spectral lines = movement toward. Doppler shift measurements demonstrate that all galaxies, except the nearest the Milky Way, show redshifts in their spectra. The closest galaxies show blueshifts due to local gravitational effects. All galaxies show redshifts on large scales in the universe. Expanding Universe: Hubble’s Law • If we measure distances and velocities, we find Hubble’s law. => The recession velocity of a galaxy is proportional to the distance of that galaxy. Hubble constant (H0): constant of proportionality. y = mx + b Hubble’s Law: v = Hod v = Ho d + 0 1. find distances to “nearby” galaxies using standard candles 2. use spectra to find recessional velocities 3. fit slope to data 4. find recessional velocities of far galaxies 5. d = v/Ho 400 Mpc =1.3x109 light years 16 .
Load more

Recommended publications
  • The Age of the Universe Transcript
    The Age of the Universe Transcript Date: Wednesday, 6 February 2013 - 1:00PM Location: Museum of London 6 February 2013 The Age of The Universe Professor Carolin Crawford Introduction The idea that the Universe might have an age is a relatively new concept, one that became recognised only during the past century. Even as it became understood that individual objects, such as stars, have finite lives surrounded by a birth and an end, the encompassing cosmos was always regarded as a static and eternal framework. The change in our thinking has underpinned cosmology, the science concerned with the structure and the evolution of the Universe as a whole. Before we turn to the whole cosmos then, let us start our story nearer to home, with the difficulty of solving what might appear a simpler problem, determining the age of the Earth. Age of the Earth The fact that our planet has evolved at all arose predominantly from the work of 19th century geologists, and in particular, the understanding of how sedimentary rocks had been set down as an accumulation of layers over extraordinarily long periods of time. The remains of creatures trapped in these layers as fossils clearly did not resemble any currently living, but there was disagreement about how long a time had passed since they had died. The cooling earth The first attempt to age the Earth based on physics rather than geology came from Lord Kelvin at the end of the 19th Century. Assuming that the whole planet would have started from a completely molten state, he then calculated how long it would take for the surface layers of Earth to cool to their present temperature.
    [Show full text]
  • Hubble's Law and the Expanding Universe
    COMMENTARY COMMENTARY Hubble’s Law and the expanding universe Neta A. Bahcall1 the expansion rate is constant in all direc- Department of Astrophysical Sciences, Princeton University, Princeton, NJ 08544 tions at any given time, this rate changes with time throughout the life of the uni- verse. When expressed as a function of cos- In one of the most famous classic papers presented the observational evidence for one H t in the annals of science, Edwin Hubble’s of science’s greatest discoveries—the expand- mic time, ( ), it is known as the Hubble 1929 PNAS article on the observed relation inguniverse.Hubbleshowedthatgalaxiesare Parameter. The expansion rate at the pres- between distance and recession velocity of receding away from us with a velocity that is ent time, Ho, is about 70 km/s/Mpc (where 1 Mpc = 106 parsec = 3.26 × 106 light-y). galaxies—the Hubble Law—unveiled the proportional to their distance from us: more The inverse of the Hubble Constant is the expanding universe and forever changed our distant galaxies recede faster than nearby gal- Hubble Time, tH = d/v = 1/H ; it reflects understanding of the cosmos. It inaugurated axies. Hubble’s classic graph of the observed o the time since a linear cosmic expansion has the field of observational cosmology that has velocity vs. distance for nearby galaxies is begun (extrapolating a linear Hubble Law uncovered an amazingly vast universe that presented in Fig. 1; this graph has become back to time t = 0); it is thus related to has been expanding and evolving for 14 bil- a scientific landmark that is regularly repro- the age of the Universe from the Big-Bang lion years and contains dark matter, dark duced in astronomy textbooks.
    [Show full text]
  • The Reionization of Cosmic Hydrogen by the First Galaxies Abstract 1
    David Goodstein’s Cosmology Book The Reionization of Cosmic Hydrogen by the First Galaxies Abraham Loeb Department of Astronomy, Harvard University, 60 Garden St., Cambridge MA, 02138 Abstract Cosmology is by now a mature experimental science. We are privileged to live at a time when the story of genesis (how the Universe started and developed) can be critically explored by direct observations. Looking deep into the Universe through powerful telescopes, we can see images of the Universe when it was younger because of the finite time it takes light to travel to us from distant sources. Existing data sets include an image of the Universe when it was 0.4 million years old (in the form of the cosmic microwave background), as well as images of individual galaxies when the Universe was older than a billion years. But there is a serious challenge: in between these two epochs was a period when the Universe was dark, stars had not yet formed, and the cosmic microwave background no longer traced the distribution of matter. And this is precisely the most interesting period, when the primordial soup evolved into the rich zoo of objects we now see. The observers are moving ahead along several fronts. The first involves the construction of large infrared telescopes on the ground and in space, that will provide us with new photos of the first galaxies. Current plans include ground-based telescopes which are 24-42 meter in diameter, and NASA’s successor to the Hubble Space Telescope, called the James Webb Space Telescope. In addition, several observational groups around the globe are constructing radio arrays that will be capable of mapping the three-dimensional distribution of cosmic hydrogen in the infant Universe.
    [Show full text]
  • Galaxies at High Redshift Mauro Giavalisco
    eaa.iop.org DOI: 10.1888/0333750888/1669 Galaxies at High Redshift Mauro Giavalisco From Encyclopedia of Astronomy & Astrophysics P. Murdin © IOP Publishing Ltd 2006 ISBN: 0333750888 Institute of Physics Publishing Bristol and Philadelphia Downloaded on Thu Mar 02 23:08:45 GMT 2006 [131.215.103.76] Terms and Conditions Galaxies at High Redshift E NCYCLOPEDIA OF A STRONOMY AND A STROPHYSICS Galaxies at High Redshift that is progressively higher for objects that are separated in space by larger distances. If the recession velocity between Galaxies at high REDSHIFT are very distant galaxies and, two objects is small compared with the speed of light, since light propagates through space at a finite speed of its value is directly proportional to the distance between approximately 300 000 km s−1, they appear to an observer them, namely v = H d on the Earth as they were in a very remote past, when r 0 the light departed them, carrying information on their H properties at that time. Observations of objects with very where the constant of proportionality 0 is called the high redshifts play a central role in cosmology because ‘HUBBLE CONSTANT’. For larger recession velocities this they provide insight into the epochs and the mechanisms relation is replaced by a more general one calculated from the theory of general relativity. In each cases, the value of GALAXY FORMATION, if one can reach redshifts that are high H enough to correspond to the cosmic epochs when galaxies of 0 provides the recession velocity of a pair of galaxies were forming their first populations of stars and began to separated by unitary distance, and hence sets the rate of shine light throughout space.
    [Show full text]
  • The Anthropic Principle and Multiple Universe Hypotheses Oren Kreps
    The Anthropic Principle and Multiple Universe Hypotheses Oren Kreps Contents Abstract ........................................................................................................................................... 1 Introduction ..................................................................................................................................... 1 Section 1: The Fine-Tuning Argument and the Anthropic Principle .............................................. 3 The Improbability of a Life-Sustaining Universe ....................................................................... 3 Does God Explain Fine-Tuning? ................................................................................................ 4 The Anthropic Principle .............................................................................................................. 7 The Multiverse Premise ............................................................................................................ 10 Three Classes of Coincidence ................................................................................................... 13 Can The Existence of Sapient Life Justify the Multiverse? ...................................................... 16 How unlikely is fine-tuning? .................................................................................................... 17 Section 2: Multiverse Theories ..................................................................................................... 18 Many universes or all possible
    [Show full text]
  • Year 1 Cosmology Results from the Dark Energy Survey
    Year 1 Cosmology Results from the Dark Energy Survey Elisabeth Krause on behalf of the Dark Energy Survey collaboration TeVPA 2017, Columbus OH Our Simple Universe On large scales, the Universe can be modeled with remarkably few parameters age of the Universe geometry of space density of atoms density of matter amplitude of fluctuations scale dependence of fluctuations [of course, details often not quite as simple] Our Puzzling Universe Ordinary Matter “Dark Energy” accelerates the expansion 5% dominates the total energy density smoothly distributed 25% acceleration first measured by SN 1998 “Dark Matter” 70% Our Puzzling Universe Ordinary Matter “Dark Energy” accelerates the expansion 5% dominates the total energy density smoothly distributed 25% acceleration first measured by SN 1998 “Dark Matter” next frontier: understand cosmological constant Λ: w ≡P/ϱ=-1? 70% magnitude of Λ very surprising dynamic dark energy varying in time and space, w(a)? breakdown of GR? Theoretical Alternatives to Dark Energy Many new DE/modified gravity theories developed over last decades Most can be categorized based on how they break GR: The only local, second-order gravitational field equations that can be derived from a four-dimensional action that is constructed solely from the metric tensor, and admitting Bianchi identities, are GR + Λ. Lovelock’s theorem (1969) [subject to viability conditions] Theoretical Alternatives to Dark Energy Many new DE/modified gravity theories developed over last decades Most can be categorized based on how they break GR: The only local, second-order gravitational field equations that can be derived from a four-dimensional action that is constructed solely from the metric tensor, and admitting Bianchi identities, are GR + Λ.
    [Show full text]
  • Understanding the H2/HI Ratio in Galaxies 3
    Mon. Not. R. Astron. Soc. 394, 1857–1874 (2009) Printed 6 August 2021 (MN LATEX style file v2.2) Understanding the H2/HI Ratio in Galaxies D. Obreschkow and S. Rawlings Astrophysics, Department of Physics, University of Oxford, Keble Road, Oxford, OX1 3RH, UK Accepted 2009 January 12 ABSTRACT galaxy We revisit the mass ratio Rmol between molecular hydrogen (H2) and atomic hydrogen (HI) in different galaxies from a phenomenological and theoretical viewpoint. First, the local H2- mass function (MF) is estimated from the local CO-luminosity function (LF) of the FCRAO Extragalactic CO-Survey, adopting a variable CO-to-H2 conversion fitted to nearby observa- 5 1 tions. This implies an average H2-density ΩH2 = (6.9 2.7) 10− h− and ΩH2 /ΩHI = 0.26 0.11 ± · galaxy ± in the local Universe. Second, we investigate the correlations between Rmol and global galaxy properties in a sample of 245 local galaxies. Based on these correlations we intro- galaxy duce four phenomenological models for Rmol , which we apply to estimate H2-masses for galaxy each HI-galaxy in the HIPASS catalog. The resulting H2-MFs (one for each model for Rmol ) are compared to the reference H2-MF derived from the CO-LF, thus allowing us to determine the Bayesian evidence of each model and to identify a clear best model, in which, for spi- galaxy ral galaxies, Rmol negatively correlates with both galaxy Hubble type and total gas mass. galaxy Third, we derive a theoretical model for Rmol for regular galaxies based on an expression for their axially symmetric pressure profile dictating the degree of molecularization.
    [Show full text]
  • Cosmic Microwave Background
    1 29. Cosmic Microwave Background 29. Cosmic Microwave Background Revised August 2019 by D. Scott (U. of British Columbia) and G.F. Smoot (HKUST; Paris U.; UC Berkeley; LBNL). 29.1 Introduction The energy content in electromagnetic radiation from beyond our Galaxy is dominated by the cosmic microwave background (CMB), discovered in 1965 [1]. The spectrum of the CMB is well described by a blackbody function with T = 2.7255 K. This spectral form is a main supporting pillar of the hot Big Bang model for the Universe. The lack of any observed deviations from a 7 blackbody spectrum constrains physical processes over cosmic history at redshifts z ∼< 10 (see earlier versions of this review). Currently the key CMB observable is the angular variation in temperature (or intensity) corre- lations, and to a growing extent polarization [2–4]. Since the first detection of these anisotropies by the Cosmic Background Explorer (COBE) satellite [5], there has been intense activity to map the sky at increasing levels of sensitivity and angular resolution by ground-based and balloon-borne measurements. These were joined in 2003 by the first results from NASA’s Wilkinson Microwave Anisotropy Probe (WMAP)[6], which were improved upon by analyses of data added every 2 years, culminating in the 9-year results [7]. In 2013 we had the first results [8] from the third generation CMB satellite, ESA’s Planck mission [9,10], which were enhanced by results from the 2015 Planck data release [11, 12], and then the final 2018 Planck data release [13, 14]. Additionally, CMB an- isotropies have been extended to smaller angular scales by ground-based experiments, particularly the Atacama Cosmology Telescope (ACT) [15] and the South Pole Telescope (SPT) [16].
    [Show full text]
  • Atlas Menor Was Objects to Slowly Change Over Time
    C h a r t Atlas Charts s O b by j Objects e c t Constellation s Objects by Number 64 Objects by Type 71 Objects by Name 76 Messier Objects 78 Caldwell Objects 81 Orion & Stars by Name 84 Lepus, circa , Brightest Stars 86 1720 , Closest Stars 87 Mythology 88 Bimonthly Sky Charts 92 Meteor Showers 105 Sun, Moon and Planets 106 Observing Considerations 113 Expanded Glossary 115 Th e 88 Constellations, plus 126 Chart Reference BACK PAGE Introduction he night sky was charted by western civilization a few thou - N 1,370 deep sky objects and 360 double stars (two stars—one sands years ago to bring order to the random splatter of stars, often orbits the other) plotted with observing information for T and in the hopes, as a piece of the puzzle, to help “understand” every object. the forces of nature. The stars and their constellations were imbued with N Inclusion of many “famous” celestial objects, even though the beliefs of those times, which have become mythology. they are beyond the reach of a 6 to 8-inch diameter telescope. The oldest known celestial atlas is in the book, Almagest , by N Expanded glossary to define and/or explain terms and Claudius Ptolemy, a Greco-Egyptian with Roman citizenship who lived concepts. in Alexandria from 90 to 160 AD. The Almagest is the earliest surviving astronomical treatise—a 600-page tome. The star charts are in tabular N Black stars on a white background, a preferred format for star form, by constellation, and the locations of the stars are described by charts.
    [Show full text]
  • Arxiv:2002.11464V1 [Physics.Gen-Ph] 13 Feb 2020 a Function of the Angles Θ and Φ in the Sky Is Shown in Fig
    Flat Space, Dark Energy, and the Cosmic Microwave Background Kevin Cahill Department of Physics and Astronomy University of New Mexico Albuquerque, New Mexico 87106 (Dated: February 27, 2020) This paper reviews some of the results of the Planck collaboration and shows how to compute the distance from the surface of last scattering, the distance from the farthest object that will ever be observed, and the maximum radius of a density fluctuation in the plasma of the CMB. It then explains how these distances together with well-known astronomical facts imply that space is flat or nearly flat and that dark energy is 69% of the energy of the universe. I. COSMIC MICROWAVE BACKGROUND RADIATION The cosmic microwave background (CMB) was predicted by Gamow in 1948 [1], estimated to be at a temperature of 5 K by Alpher and Herman in 1950 [2], and discovered by Penzias and Wilson in 1965 [3]. It has been observed in increasing detail by Roll and Wilkinson in 1966 [4], by the Cosmic Background Explorer (COBE) collaboration in 1989{1993 [5, 6], by the Wilkinson Microwave Anisotropy Probe (WMAP) collaboration in 2001{2013 [7, 8], and by the Planck collaboration in 2009{2019 [9{12]. The Planck collaboration measured CMB radiation at nine frequencies from 30 to 857 6 GHz by using a satellite at the Lagrange point L2 in the Earth's shadow some 1.5 10 km × farther from the Sun [11, 12]. Their plot of the temperature T (θ; φ) of the CMB radiation as arXiv:2002.11464v1 [physics.gen-ph] 13 Feb 2020 a function of the angles θ and φ in the sky is shown in Fig.
    [Show full text]
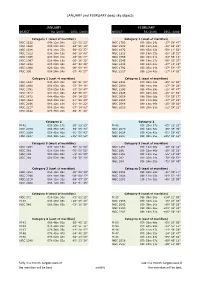
  • SPIRIT Target Lists
    JANUARY and FEBRUARY deep sky objects JANUARY FEBRUARY OBJECT RA (2000) DECL (2000) OBJECT RA (2000) DECL (2000) Category 1 (west of meridian) Category 1 (west of meridian) NGC 1532 04h 12m 04s -32° 52' 23" NGC 1792 05h 05m 14s -37° 58' 47" NGC 1566 04h 20m 00s -54° 56' 18" NGC 1532 04h 12m 04s -32° 52' 23" NGC 1546 04h 14m 37s -56° 03' 37" NGC 1672 04h 45m 43s -59° 14' 52" NGC 1313 03h 18m 16s -66° 29' 43" NGC 1313 03h 18m 15s -66° 29' 51" NGC 1365 03h 33m 37s -36° 08' 27" NGC 1566 04h 20m 01s -54° 56' 14" NGC 1097 02h 46m 19s -30° 16' 32" NGC 1546 04h 14m 37s -56° 03' 37" NGC 1232 03h 09m 45s -20° 34' 45" NGC 1433 03h 42m 01s -47° 13' 19" NGC 1068 02h 42m 40s -00° 00' 48" NGC 1792 05h 05m 14s -37° 58' 47" NGC 300 00h 54m 54s -37° 40' 57" NGC 2217 06h 21m 40s -27° 14' 03" Category 1 (east of meridian) Category 1 (east of meridian) NGC 1637 04h 41m 28s -02° 51' 28" NGC 2442 07h 36m 24s -69° 31' 50" NGC 1808 05h 07m 42s -37° 30' 48" NGC 2280 06h 44m 49s -27° 38' 20" NGC 1792 05h 05m 14s -37° 58' 47" NGC 2292 06h 47m 39s -26° 44' 47" NGC 1617 04h 31m 40s -54° 36' 07" NGC 2325 07h 02m 40s -28° 41' 52" NGC 1672 04h 45m 43s -59° 14' 52" NGC 3059 09h 50m 08s -73° 55' 17" NGC 1964 05h 33m 22s -21° 56' 43" NGC 2559 08h 17m 06s -27° 27' 25" NGC 2196 06h 12m 10s -21° 48' 22" NGC 2566 08h 18m 46s -25° 30' 02" NGC 2217 06h 21m 40s -27° 14' 03" NGC 2613 08h 33m 23s -22° 58' 22" NGC 2442 07h 36m 20s -69° 31' 29" Category 2 Category 2 M 42 05h 35m 17s -05° 23' 25" M 42 05h 35m 17s -05° 23' 25" NGC 2070 05h 38m 38s -69° 05' 39" NGC 2070 05h 38m 38s -69°
    [Show full text]
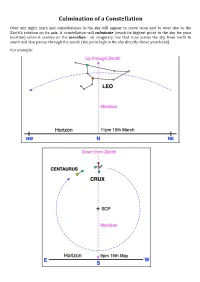
  • Culmination of a Constellation
    Culmination of a Constellation Over any night, stars and constellations in the sky will appear to move from east to west due to the Earth’s rotation on its axis. A constellation will culminate (reach its highest point in the sky for your location) when it centres on the meridian - an imaginary line that runs across the sky from north to south and also passes through the zenith (the point high in the sky directly above your head). For example: When to Observe Constellations The taBle shows the approximate time (AEST) constellations will culminate around the middle (15th day) of each month. Constellations will culminate 2 hours earlier for each successive month. Note: add an hour to the given time when daylight saving time is in effect. The time “12” is midnight. Sunrise/sunset times are rounded off to the nearest half an hour. Sun- Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec Rise 5am 5:30 6am 6am 7am 7am 7am 6:30 6am 5am 4:30 4:30 Set 7pm 6:30 6pm 5:30 5pm 5pm 5pm 5:30 6pm 6pm 6:30 7pm And 5am 3am 1am 11pm 9pm Aqr 5am 3am 1am 11pm 9pm Aql 4am 2am 12 10pm 8pm Ara 4am 2am 12 10pm 8pm Ari 5am 3am 1am 11pm 9pm Aur 10pm 8pm 4am 2am 12 Boo 3am 1am 11pm 9pm 7pm Cnc 1am 11pm 9pm 7pm 3am CVn 3am 1am 11pm 9pm 7pm CMa 11pm 9pm 7pm 3am 1am Cap 5am 3am 1am 11pm 9pm 7pm Car 2am 12 10pm 8pm 6pm Cen 4am 2am 12 10pm 8pm 6pm Cet 4am 2am 12 10pm 8pm Cha 3am 1am 11pm 9pm 7pm Col 10pm 8pm 4am 2am 12 Com 3am 1am 11pm 9pm 7pm CrA 3am 1am 11pm 9pm 7pm CrB 4am 2am 12 10pm 8pm Crv 3am 1am 11pm 9pm 7pm Cru 3am 1am 11pm 9pm 7pm Cyg 5am 3am 1am 11pm 9pm 7pm Del
    [Show full text]