DOCSLIB.ORG

Coordination Chemistry of Actinide and Lanthanide Ions

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Coordination Chemistry of Actinide and Lanthanide Ions Coordination Chemistry of Actinide and Lanthanide Ions Ildikó Farkas Doctoral Thesis Stockholm 2001 Department of Chemistry Inorganic Chemistry Royal Institute of Technology S-100 44 Stockholm, Sweden Department of Chemistry Inorganic Chemistry Royal Institute of Technology S-100 44 Stockholm, Sweden Coordination Chemistry of Actinide and Lanthanide Ions Ildikó Farkas AKADEMISK AVHANDLING som med tillstånd av Kungliga Tekniska Högskolan framlägges till offentlig granskning för avläggande av filosofie doktorsexamen i oorganisk kemi, fredagen den 26 oktober 2001, kl 14.00 i K2, KTH. Fakultetsopponent är Professor Staffan Sjöberg. Avhandlingen försvaras på engelska. Abstract Water exchange of the actinide ions, U(IV), U(VI) and Th(IV), in 4 m NaClO4 media as well as coordination chemistry of lanthanide(III) ions with the glycolate ligand are discussed in this thesis. 2+ 4+ 3+ The activation parameters for the water exchange reaction of UO2 (aq), U (aq), UF (aq) and a lower limit for the water exchange rate constant at room temperature for Th4+(aq) have been determined by 17O NMR relaxation techniques. For the paramagnetic U4+(aq) and UF3+(aq) ions, 2+ 4+ the water exchange was studied directly, while for the diamagnetic UO2 (aq) and Th (aq), 3+ 2+ Tb (aq) was used as a chemical shift reagent. The results for UO2 are in fairly good agreement 2+ with other kinetic data. It is interesting to note that in contrast to UO2 , the rate of water exchange on U4+ is not significantly influenced by ligands as OH- or F-. Based on the known coordination 2+ geometry of UO2 (aq) and also using information obtained in quantum chemical calculations, an 2+ associative or interchange mechanism was suggested for the water exchange in UO2 (aq). The calculated activation energy is in agreement with the experimental data. Since the coordination number of water in U4+(aq) is uncertain, 9 or 10, it is rather difficult to make propositions about the mechanism of the water exchange for this ion. However, the experimental data indicate an interchange mechanism. The complexation at high pH between glycolate and different lanthanide(III) ions, Sm3+, Eu3+, Dy3+, Er3+ and Lu3+ has been studied by potentiometry and spectroscopic techniques. Based on this information a series of di- and tetranuclear ternary complexes were identified. By combination of the experimental information from solid-state structures, spectroscopy and potentiometry, the proposed constitution of these complexes are 2- -x [Ln2(OCH2COO)2(HOCH2COO)4(H2O)x] and [Ln4(OCH2COO)4(OCH2COO)x(HOCH2COO)4-x] , with x = 2-4. The oxyacetate is formed by deprotonation of the α-OH group in the glycolate as a result of the very strong inductive effect of the metal ion. The “Ln4(OCH2COO)4” unit has a cubane like structure where the oxy group act as a bridge between three Ln atoms. A structure study is also part of the work, providing supporting information about the formation of oxyacetate complexes. The crystal structure of the sodium salt of the uranyl- oxyacetate-fluoride dimer, Na4(UO2)2(OCH2COO)2F4·6H2O as well as that of some lanthanide- glycolates, Lu(HOCH2COO)3·2H2O and Dy2(OCH2COO)2(HOCH2COO)2·4H2O, have been determined by single crystal X-ray diffraction. In the Dy2(OCH2COO)2(HOCH2COO)2·4H2O structure with a dysprosium-oxyacetate dimer core, the dysprosium ions have a coordination number of eight and the geometry is distorted dodecahedral. The structure consists of a three- dimensional network of cross-linked metal-ligand chains, while the other lanthanide crystal, + Lu(HOCH2COO)3·2H2O, consists of discrete eight-coordinated cationic Lu(HOCH2COO)2(H2O)4 - and anionic Lu(HOCH2COO)4 complexes. Keywords: water exchange, dynamics, uranium(IV), uranyl, thorium(IV), aqua ions, fluoride, 17O NMR relaxation techniques, terbium(III), potentiometry, lanthanides, glycolate, α-OH group, deprotonation, X-ray crystallography, TRLFS, NMR. Preface This work was started at Inorganic Chemistry, KTH as a joint venture with the Physical Chemistry Department, Lajos Kossuth University (KLTE), Debrecen, Hungary. I entered the project at the KLTE in September 1996, and one year later I continued it at the Department of Chemistry, Inorganic Chemistry, Royal Institute of Technology, Stockholm. My supervisors at that time were István Bányai and Professor Ingmar Grenthe. I took the licentiate exam in 1999 based on the water and electron exchange studies; the latter one is not part of this doctoral thesis. After one- year break in 2000 I started to work with potentiometry at the KTH under Prof. Ingmar Grenthe’s and Dr. Zoltán Szabó’s supervision. The thesis is based on the following publications: 2+ Paper I “Rates and Mechanisms of Water Exchange of UO2 (aq) and - 17 19 UO2(oxalate)F(H2O)2 : A Variable Temperature O and F NMR Study.” Ildikó Farkas, István Bányai, Zoltán Szabó, Ulf Wahlgren and Ingmar Grenthe Inorg. Chem. 2000, 39(4), 799 Paper II “The Rates and Mechanisms of Water exchange of Actinide Aqua 17 4+ Ions: A Variable Temperature O NMR study of U(H2O)10 , 3+ 4+ UF(H2O)9 , and Th(H2O)10 .” István Bányai, Ildikó Farkas and Ingmar Grenthe J. Phys. Chem. A 2000, 104, 1201 Paper III “Crystal structure of the sodium salt of the uranyl-oxyacetate-fluoride dimer, Na4(UO2)2(OCH2COO)2F4·6H2O.” Ildikó Farkas, Ingeborg Csöregh and Zoltán Szabó Acta Chem. Scand. 1999, 53, 1009 Paper IV “Crystal structure of some lanthanide(III)-glycolate complexes, Lu(HOCH2COO)3·2H2O and Dy2(OCH2COO)2(HOCH2COO)2·4H2O. An X-ray Diffraction and Vibrational Spectroscopic Study.” Ildikó Farkas, Andreas Fischer and Martin Lindsjö submitted to J. Chem. Soc., Dalton Trans. Paper V “Complexation of Cm(III) and lanthanide(III) ions by glycolic acid: TRLFS, potentiometric, vibrational and NMR spectroscopic studies.” Thorsten Stumpf, Ildikó Farkas, Thomas Fanghänel, Zoltán Szabó and Ingmar Grenthe under way Table of Contents I Introduction 1 II Water Exchange on Actinide Ions 4 II.1 Background 4 II.1.1 General remarks 4 II.1.2 Previous studies on the water exchange of uranyl ion 5 II.2 Experimental methods 6 II.2.1 NMR relaxation techniques 6 II.2.2 Determination of activation parameters 10 II.3 Study on the water exchange of actinide ions 11 II.3.1 An important parameter: the coordination number of aqua ions 11 II.3.2 Conclusions 13 III Coordination Chemistry of Lanthanide(III)-, Uranyl- and Actinide(III)- Glycolate Systems 20 III.1 General remarks 20 III.2 Previous studies on the complexation of uranyl and lanthanide(III) with glycolate ligand 21 III.2.1 Complexation of glycolate with uranyl ion 22 III.2.1 Complexation of glycolate with lanthanide(III) ions 22 III.3 Potentiometric study on lanthanide(III)-glycolate systems 23 III.3.1 Experimental background 23 III.3.1.1 Solution chemical equilibrium 23 III.3.1.2 Equilibrium analysis by potentiometry 23 III.3.1.2.1 Measurement of [H+] with glass electrode 24 III.3.1.2.2 Equilibrium calculations in a three-component metal-ligand-proton system 25 III.3.1.2.3 A special case: a three-component system reduced to two components 28 III.3.1.3 Activity coefficients 30 III.3.2 Potentiometric titration results in lanthanide-glycolate systems 32 III.4 Spectroscopic studies on lanthanide(III)- and actinide(III)- glycolate solutions 35 III.4.1 Time resolved laser fluorescence spectroscopic study of actinide(III)-glycolate solutions 35 III.4.2 Vibrational spectroscopic measurements in Dy(III)- glycolate solutions 37 III.4.3 Lu(III)-glycolate solutions studied by NMR spectroscopy 37 III.5 Crystallographic study on lanthanide(III)- and uranyl- glycolate complexes 39 III.5.1 Crystal structure of a uranyl-oxyacetate-fluoride dimer 40 III.5.2 Crystal structure of some lanthanide(III)-glycolate and oxyacetate complexes 42 III.5.2.1 Crystal structure of Lu(HOCH2COO)3·2H2O 42 III.5.2.2 Crystal structure of Dy2(OCH2COO)2(HOCH2COO)2·4H2O 44 III.6 Constitution and structure of the lanthanide- glycolate/oxyacetate complexes 46 IV Conclusions and Future Work 48 References 50 I Introduction Study of water exchange of some actinide ions in aqueous solution, as well as the coordination chemistry of lanthanide-glycolate complexes are discussed in this thesis. In coordination chemistry, simple chemical systems are used to develop and verify the scientific theories that are necessary to predict the behaviour of more complicated systems. The study of the water exchange and the coordination chemistry of actinide ions in aqueous solution is necessary for the understanding of homogeneous and heterogeneous chemical processes in which these ions are involved. Examples of such processes range from laboratory systems to the much more complex ones encountered in engineering (such as nuclear fuel reprocessing plants or repositories for radioactive waste) or in nature (geochemical processes for uranium ore formation, or the transport of radionuclides in ground and surface water systems). There are large chemical similarities between the chemistry of the M3+ ions in the lanthanide and actinide groups, but differences also occur and they can be exploited e.g. to find new methods for their separation, a difficult task, as their chemical characteristics are very similar. Lanthanide complexes are becoming more and more important in medical diagnostic techniques using NMR spin imaging, in catalysis and in organic synthesis, which is another reason to develop a deeper understanding of their chemistry. The chemical properties of the elements are determined by their electron structure. In the lanthanide series the electrons of the 4f sub-shell are practically part of the core therefore the +3 oxidation state, studied here, dominates their chemistry. The chemical properties in the same oxidation state of the 4f and 5f elements are very similar. When studying the chemistry of the lanthanides, one often observes smooth changes between the elements, which can be attributed to the ionic radius decreasing with the atomic number along the series.
Load more

Recommended publications
  • A Protein Engineered to Bind Uranyl Selectively and with Femtomolar Affinity
    ARTICLES PUBLISHED ONLINE: 26 JANUARY 2014 | DOI: 10.1038/NCHEM.1856 A protein engineered to bind uranyl selectively and with femtomolar affinity Lu Zhou1†, Mike Bosscher1†, Changsheng Zhang2,3†,SalihO¨ zc¸ubukc¸u1, Liang Zhang1, Wen Zhang1, Charles J. Li1, Jianzhao Liu1, Mark P. Jensen4, Luhua Lai2,3* and Chuan He1* 21 ∼ Uranyl (UO2 ), the predominant aerobic form of uranium, is present in the ocean at a concentration of 3.2 parts per 109 (13.7 nM); however, the successful enrichment of uranyl from this vast resource has been limited by the high concentrations of metal ions of similar size and charge, which makes it difficult to design a binding motif that is selective for uranyl. Here we report the design and rational development of a uranyl-binding protein using a computational screening process in the initial search for potential uranyl-binding sites. The engineered protein is thermally stable and offers very high affinity and selectivity for uranyl with a Kd of 7.4 femtomolar (fM) and >10,000-fold selectivity over other metal ions. We also demonstrated that the uranyl-binding protein can repeatedly sequester 30–60% of the uranyl in synthetic sea water. The chemical strategy employed here may be applied to engineer other selective metal-binding proteins for biotechnology and remediation applications. ranium is the key element for nuclear-energy production and Through billions of years of evolution nature has produced is important in many other applications. The most stable and strategies to recognize beneficial or toxic metal ions with high Urelevant uranium ion in aerobic environments is the uranyl sensitivity and selectivity.
    [Show full text]
  • Hierarchically-Structured Metalloprotein Composite
    ARTICLE There are amendments to this paper https://doi.org/10.1038/s41467-020-14709-y OPEN Hierarchically-structured metalloprotein composite coatings biofabricated from co-existing condensed liquid phases ✉ Franziska Jehle 1, Elena Macías-Sánchez1, Sanja Sviben1, Peter Fratzl1, Luca Bertinetti 1 & ✉ Matthew J. Harrington 1,2 1234567890():,; Complex hierarchical structure governs emergent properties in biopolymeric materials; yet, the material processing involved remains poorly understood. Here, we investigated the multi- scale structure and composition of the mussel byssus cuticle before, during and after for- mation to gain insight into the processing of this hard, yet extensible metal cross-linked protein composite. Our findings reveal that the granular substructure crucial to the cuticle’s function as a wear-resistant coating of an extensible polymer fiber is pre-organized in con- densed liquid phase secretory vesicles. These are phase-separated into DOPA-rich proto- granules enveloped in a sulfur-rich proto-matrix which fuses during secretion, forming the sub-structure of the cuticle. Metal ions are added subsequently in a site-specific way, with iron contained in the sulfur-rich matrix and vanadium coordinated by DOPA-catechol in the granule. We posit that this hierarchical structure self-organizes via phase separation of specific amphiphilic proteins within secretory vesicles, resulting in a meso-scale structuring that governs cuticle function. 1 Department of Biomaterials, Max Planck Institute of Colloids and Interfaces, 14424 Potsdam,
    [Show full text]
  • Depleted Uranium Technical Brief
    Disclaimer - For assistance accessing this document or additional information,please contact [email protected]. Depleted Uranium Technical Brief United States Office of Air and Radiation EPA-402-R-06-011 Environmental Protection Agency Washington, DC 20460 December 2006 Depleted Uranium Technical Brief EPA 402-R-06-011 December 2006 Project Officer Brian Littleton U.S. Environmental Protection Agency Office of Radiation and Indoor Air Radiation Protection Division ii iii FOREWARD The Depleted Uranium Technical Brief is designed to convey available information and knowledge about depleted uranium to EPA Remedial Project Managers, On-Scene Coordinators, contractors, and other Agency managers involved with the remediation of sites contaminated with this material. It addresses relative questions regarding the chemical and radiological health concerns involved with depleted uranium in the environment. This technical brief was developed to address the common misconception that depleted uranium represents only a radiological health hazard. It provides accepted data and references to additional sources for both the radiological and chemical characteristics, health risk as well as references for both the monitoring and measurement and applicable treatment techniques for depleted uranium. Please Note: This document has been changed from the original publication dated December 2006. This version corrects references in Appendix 1 that improperly identified the content of Appendix 3 and Appendix 4. The document also clarifies the content of Appendix 4. iv Acknowledgments This technical bulletin is based, in part, on an engineering bulletin that was prepared by the U.S. Environmental Protection Agency, Office of Radiation and Indoor Air (ORIA), with the assistance of Trinity Engineering Associates, Inc.
    [Show full text]
  • A Structural and Spectroscopic Study of the First Uranyl Selenocyanate, [Et4n]3[UO2(Ncse)5]
    inorganics Article A Structural and Spectroscopic Study of the First Uranyl Selenocyanate, [Et4N]3[UO2(NCSe)5] Stefano Nuzzo, Michelle P. Browne, Brendan Twamley, Michael E. G. Lyons and Robert J. Baker * School of Chemistry, Trinity College, University of Dublin, 2 Dublin, Ireland; [email protected] (S.N.); [email protected] (M.P.B.); [email protected] (B.T.); [email protected] (M.E.G.L.) * Correspondence: [email protected]; Tel.: +353-1-896-3501; Fax: +353-1-671-2826 Academic Editors: Stephen Mansell and Steve Liddle Received: 30 October 2015; Accepted: 4 February 2016; Published: 16 February 2016 Abstract: The first example of a uranyl selenocyanate compound is reported. The compound [Et4N]3[UO2(NCSe)5] has been synthesized and fully characterized by vibrational and multinuclear (1H, 13C{1H} and 77Se{1H}) NMR spectroscopy. The photophysical properties have also been recorded and trends in a series of uranyl pseudohalides discussed. Spectroscopic evidence shows that the U–NCSe bonding is principally ionic. An electrochemical study revealed that the reduced uranyl(V) species is unstable to disproportionation and a ligand based oxidation is also observed. The structure of [Et4N]4[UO2(NCSe)5][NCSe] is also presented and Se¨ ¨ ¨ H–C hydrogen bonding and Se¨ ¨ ¨ Se chalcogen–chalcogen interactions are seen. Keywords: uranyl; structural determination; photophysics 1. Introduction The chemistry of uranium in its highest oxidation state has held scientists fascination for a long 2+ period of time. The uranyl moiety, [UO2] , is well studied in aqueous phases due, in part, to relevance in the nuclear waste treatment. Moreover, the photophysical properties of uranyl were first used in ancient roman times in colored glass [1], whilst comprehensive understanding of the bonding, and therefore photophysical properties, has come from both experiment and theory.
    [Show full text]
  • Actinide Ground-State Properties-Theoretical Predictions
    Actinide Ground-State Properties Theoretical predictions John M. Wills and Olle Eriksson electron-electron correlations—the electronic energy of the ground state of or nearly fifty years, the actinides interactions among the 5f electrons and solids, molecules, and atoms as a func- defied the efforts of solid-state between them and other electrons—are tional of electron density. The DFT Ftheorists to understand their expected to affect the bonding. prescription has had such a profound properties. These metals are among Low-symmetry crystal structures, impact on basic research in both the most complex of the long-lived relativistic effects, and electron- chemistry and solid-state physics that elements, and in the solid state, they electron correlations are very difficult Walter Kohn, its main inventor, was display some of the most unusual to treat in traditional electronic- one of the recipients of the 1998 behaviors of any series in the periodic structure calculations of metals and, Nobel Prize in Chemistry. table. Very low melting temperatures, until the last decade, were outside the In general, it is not possible to apply large anisotropic thermal-expansion realm of computational ability. And DFT without some approximation. coefficients, very low symmetry crystal yet, it is essential to treat these effects But many man-years of intense research structures, many solid-to-solid phase properly in order to understand the have yielded reliable approximate transitions—the list is daunting. Where physics of the actinides. Electron- expressions for the total energy in does one begin to put together an electron correlations are important in which all terms, except for a single- understanding of these elements? determining the degree to which 5f particle kinetic-energy term, can be In the last 10 years, together with electrons are localized at lattice sites.
    [Show full text]
  • Procedure for Determining Uranium, Plutonium and Americium by Extraction-Chromatographic Procedures
    Procedure for determining uranium, plutonium and americium by extraction-chromatographic procedures H-U/Pu/Am-AWASS-01 Authors: M. Beyermann D. Obrikat Federal coordinating office for drinking water, groundwater, wastewater, sludge, waste and wastewater of nuclear power plants (Leitstelle für die Überwachung der Radioaktivität in Trinkwasser, Grundwasser, Abwasser, Klärschlamm, Reststoffen und Abfällen) ISSN 1865-8725 Version October 2000 Procedures manual for monitoring of radioactive substances in the environment and of external radiation (Messanleitungen für die „Überwachung radioaktiver Stoffe in der Umwelt und externer Strahlung“) H-U/Pu/Am-AWASS-01-01 Procedure for determining uranium, plutonium and americium by means of extraction- chromatographic procedures 1 Scope This procedure serves to simultaneously determine the uranium isotopes U-234, U-235 and U-238, the plutonium isotopes Pu-238, Pu-239 and Pu-240, as well as the americium isotope Am-241 in samples of wastewater from nuclear facilities. It furthermore offers an option of determining the curium isotopes Cm-242 and Cm-244 without further effort. For determining Pu-241, reference is made to pro- cedure H-Pu-241-AWASS-01 of these measuring instructions. 2 Sampling As far as sampling is concerned, reference is made to procedure H-SPEKT- AWASS-01 of these measuring instructions. The sample of the wastewater to be analysed is acidified with ca. 10 ml of concentrated nitric acid (14 mol·l-1) per litre to a pH of about 1. The stability of the acidic reaction needs to be monitored, in particular if the sample is stored for an extended period of time. This procedure ensures that a detection limit of 0,05 Bq·l-1 for alpha-emitters is reached in a sample volume of 0,1 litres to 0,25 litres and thus complies with the nuclear safety standard 1504 of the Nuclear Safety Standards Commission (1).
    [Show full text]
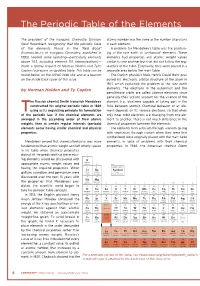
  • The Periodic Table of the Elements
    The Periodic Table of the Elements The president of the Inorganic Chemistry Division, atomic number was the same as the number of protons Gerd Rosenblatt, recognizing that the periodic table in each element. of the elements found in the “Red Book” A problem for Mendeleev’s table was the position- (Nomenclature of Inorganic Chemistry, published in ing of the rare earth or lanthanoid* elements. These 1985) needed some updating—particularly elements elements had properties and atomic weight values above 103, including element 110 (darmstadtium)— similar to one another but that did not follow the reg- made a formal request to Norman Holden and Tyler ularities of the table. Eventually, they were placed in a Coplen to prepare an updated table. This table can be separate area below the main table. found below, on the IUPAC Web site, and as a tear-off The Danish physicist Niels Henrik David Bohr pro- on the inside back cover of this issue. posed his electronic orbital structure of the atom in 1921, which explained the problem of the rare earth by Norman Holden and Ty Coplen elements. The electrons in the outermost and the penultimate orbits are called valence electrons since generally their actions account for the valence of the he Russian chemist Dmitri Ivanovich Mendeleev element (i.e., electrons capable of taking part in the constructed his original periodic table in 1869 links between atoms). Chemical behavior of an ele- Tusing as its organizing principle his formulation ment depends on its valence electrons, so that when of the periodic law: if the chemical elements are only inner orbit electrons are changing from one ele- arranged in the ascending order of their atomic ment to another, there is not much difference in the weights, then at certain regular intervals (periods) chemical properties between the elements.
    [Show full text]
  • Anion Photoelectron Spectroscopic and Relativistic Coupled-Cluster Studies of − Uranyl Dichloride Anion, Uo2cl2 Mary Marshall, Zhaoguo Zhu, Junzi Liu, Kit H
    Journal of Molecular Spectroscopy 379 (2021) 111496 Contents lists available at ScienceDirect Journal of Molecular Spectroscopy journal homepage: www.elsevier.com/locate/yjmsp Article Anion photoelectron spectroscopic and relativistic coupled-cluster studies of * uranyl dichloride anion, UO2Cl2 Mary Marshall, Zhaoguo Zhu, Junzi Liu, Kit H. Bowen, Lan Cheng < Department of Chemistry, The Johns Hopkins University, Baltimore, MD 21218, USA ARTICLEINFO ABSTRACT Keywords: A joint relativistic coupled-cluster and experimental photoelectron (PE) spectroscopic study of the uranyl Coupled-cluster * dichloride anion, UO2Cl2 , is reported. Sophisticated electronic-structure calculations predict the photodetach- Anion photoelectron * ment of UO2Cl to involve a U 5f electron and to be followed by significant geometry relaxation. Therefore, the Uranyl 2 adiabatic electron affinity (EAa) of the uranyl dichloride neutral molecule, UO2Cl2, and the vertical detachment * energy (VDE) of its anion, UO2Cl2 , provide valuable information about its uranium 5f orbital energies. The EAa value was computed to be 3.15 eV. The VDE value was calculated to be 3.55 eV by augmenting the computed EAa with a shift derived from a Franck–Condon simulation using coupled-cluster potential energy surfaces. The VDE, which corresponds to the highest intensity peak in the PE spectrum, was measured to be 3.69 , 0.20 eV, in good agreement with the computed value. The origin transition in the PE spectrum, whose electron binding energy corresponds to the EAa, was assigned to the feature at 3.2 , 0.20 eV, consistent with the computed EAa. 1. Introduction at 20323 cm*1 with nearly harmonic vibrational progressions at a frequency of 840 cm*1 [15].
    [Show full text]
  • ELECTRONEGATIVITY D Qkq F=
    ELECTRONEGATIVITY The electronegativity of an atom is the attracting power that the nucleus has for it’s own outer electrons and those of it’s neighbours i.e. how badly it wants electrons. An atom’s electronegativity is determined by Coulomb’s Law, which states, “ the size of the force is proportional to the size of the charges and inversely proportional to the square of the distance between them”. In symbols it is represented as: kq q F = 1 2 d 2 where: F = force (N) k = constant (dependent on the medium through which the force is acting) e.g. air q1 = charge on an electron (C) q2 = core charge (C) = no. of protons an outer electron sees = no. of protons – no. of inner shell electrons = main Group Number d = distance of electron from the nucleus (m) Examples of how to calculate the core charge: Sodium – Atomic number 11 Electron configuration 2.8.1 Core charge = 11 (no. of p+s) – 10 (no. of inner e-s) +1 (Group i) Chlorine – Atomic number 17 Electron configuration 2.8.7 Core charge = 17 (no. of p+s) – 10 (no. of inner e-s) +7 (Group vii) J:\Sciclunm\Resources\Year 11 Chemistry\Semester1\Notes\Atoms & The Periodic Table\Electronegativity.doc Neon holds onto its own electrons with a core charge of +8, but it can’t hold any more electrons in that shell. If it was to form bonds, the electron must go into the next shell where the core charge is zero. Group viii elements do not form any compounds under normal conditions and are therefore given no electronegativity values.
    [Show full text]
  • Periodic Table of the Elements Notes
    Periodic Table of the Elements Notes Arrangement of the known elements based on atomic number and chemical and physical properties. Divided into three basic categories: Metals (left side of the table) Nonmetals (right side of the table) Metalloids (touching the zig zag line) Basic Organization by: Atomic structure Atomic number Chemical and Physical Properties Uses of the Periodic Table Useful in predicting: chemical behavior of the elements trends properties of the elements Atomic Structure Review: Atoms are made of protons, electrons, and neutrons. Elements are atoms of only one type. Elements are identified by the atomic number (# of protons in nucleus). Energy Levels Review: Electrons are arranged in a region around the nucleus called an electron cloud. Energy levels are located within the cloud. At least 1 energy level and as many as 7 energy levels exist in atoms Energy Levels & Valence Electrons Energy levels hold a specific amount of electrons: 1st level = up to 2 2nd level = up to 8 3rd level = up to 8 (first 18 elements only) The electrons in the outermost level are called valence electrons. Determine reactivity - how elements will react with others to form compounds Outermost level does not usually fill completely with electrons Using the Table to Identify Valence Electrons Elements are grouped into vertical columns because they have similar properties. These are called groups or families. Groups are numbered 1-18. Group numbers can help you determine the number of valence electrons: Group 1 has 1 valence electron. Group 2 has 2 valence electrons. Groups 3–12 are transition metals and have 1 or 2 valence electrons.
    [Show full text]
  • Novel Heterometallic Uranyl-Transition Metal Materials: Structure, Topology, and Solid State Photoluminescence Properties † ‡ ‡ § Germań E
    Article Cite This: Inorg. Chem. 2019, 58, 7243−7254 pubs.acs.org/IC Novel Heterometallic Uranyl-Transition Metal Materials: Structure, Topology, and Solid State Photoluminescence Properties † ‡ ‡ § Germań E. Gomez, J. August Ridenour, Nicole M. Byrne, Alexander P. Shevchenko, ‡ and Christopher L. Cahill*, † Instituto de Investigaciones en Tecnología Química (INTEQUI), Area de Química General e Inorganicá “Dr. G. F. Puelles,” Facultad de Química, Bioquímica y Farmacia, Chacabuco y Pedernera, Universidad Nacional de San Luis, Almirante Brown, 1455, 5700 San Luis, Argentina ‡ Department of Chemistry, The George Washington University, Science and Engineering Hall, 800 22nd Street, NW, Washington, DC 20052, United States § Samara Center for Theoretical Materials Science, Samara University, 34, Moskovskoye shosse, Samara, 443086, Russia *S Supporting Information ABSTRACT: Six new uranyl hybrid materials have been synthesized solvothermally ′ ′ ′ ′ ′′ utilizing the ligands 2,2 -bipyridine-3,3 -dicarboxylic acid (H2L) and 2,2 :6 ,2 -terpyridine (TPY). The six compounds are classified as either molecular complexes (I0O0 connectivity), · · [(UO2)(L)(TPY)] H2O(1), [Ni(TPY)2][(UO2)(L)2] 3H2O(2), and [Cu(TPY)2]- · − 0 3 [(UO2)(L)2] 3H2O(3), or 3D metal organic frameworks (MOFs, I O connectivity), · [Cu2(UO2)2(OH)(C2H3O2)(L)3(TPY)2] 6H2O(4), [Zn2(UO2)2(OH)(NO3)(C2H3O2)- · · (L)3(TPY)2] 4H2O(5), and Na[Ni(UO2)3(OH)(O)(L)3] 9H2O(6). A discussion of the influence of transition metal incorporation, chelating effects of the ligand, and synthesis conditions on the formation of uranyl materials is presented. The structure of compound 6 is of particular note due to large channel-like voids with a diameter of approximately 19.6 Å.
    [Show full text]
  • Actinide Separation Inspired by Self-Assembled Metal-Polyphenolic Nanocages
    Page 1 of 9 1 2 3 4 5 6 7 Actinide separation inspired by self-assembled metal-polyphenolic 8 9 nanocages 10 †, §, †, ‡, § † # † † ⊥ 11 Lei Mei, * Peng Ren, Qun-yan Wu, Yu-bin Ke, Jun-shan Geng, Kang Liu, Xue-qing Xing, 12 Zhi-wei Huang, † Kong-qiu Hu, † Ya-lan Liu, † Li-yong Yuan, † Guang Mo, ⊥ Zhong-hua Wu, ⊥ John K 13 Gibson, ＆ Zhi-fang Chai, †, ¶ Wei-qun Shi †, * 14 15 † Laboratory of Nuclear Energy Chemistry, Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China 16 ‡ State key Laboratory of Nuclear Resources and Environment, School of Chemistry, School of Nuclear Science and Engineering, 17 East China University of Technology, Nanchang 330013, China. 18 ⊥Beijing Synchrotron Radiation Facility, Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China 19 # Spallation Neutron Source Science Center, Dongguan 523803, China 20 ¶ Engineering Laboratory of Advanced Energy Materials, Ningbo Institute of Industrial Technology, Chinese Academy of Sciences, 21 Ningbo 315201, China 22 ＆ Chemical Sciences Division, Lawrence Berkeley National Laboratory (LBNL), Berkeley, California 94720, USA 23 KEYWORDS: actinides; nano-extraction; uranyl-organic nanocage; self-assembly; pyrogallol[4]arene 24 25 26 ABSTRACT: The separation of actinides has a vital place in nuclear fuel reprocessing, recovery of radionuclides and 27 remediation of environmental contamination. Here we propose a new paradigm of nanocluster-based actinide separation, 28 namely nano-extraction, that can achieve efficient sequestration of uranium in an unprecedented form of giant coordination 29 nanocages using a cone-shaped macrocyclic pyrogallol[4]arene as the extractant. The U24-based hexameric 30 pyrogallol[4]arene nanocages with distinctive [U2PG2] binuclear units (PG = pyrogallol), that rapidly assembled in situ in 31 monophasic solvent, were identified by single-crystal XRD, MALDI-TOF-MS, NMR, and SAXS/SANS.
    [Show full text]