Engineering a High-Performance GPU B-Tree
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Application of TRIE Data Structure and Corresponding Associative Algorithms for Process Optimization in GRID Environment
Application of TRIE data structure and corresponding associative algorithms for process optimization in GRID environment V. V. Kashanskya, I. L. Kaftannikovb South Ural State University (National Research University), 76, Lenin prospekt, Chelyabinsk, 454080, Russia E-mail: a [email protected], b [email protected] Growing interest around different BOINC powered projects made volunteer GRID model widely used last years, arranging lots of computational resources in different environments. There are many revealed problems of Big Data and horizontally scalable multiuser systems. This paper provides an analysis of TRIE data structure and possibilities of its application in contemporary volunteer GRID networks, including routing (L3 OSI) and spe- cialized key-value storage engine (L7 OSI). The main goal is to show how TRIE mechanisms can influence de- livery process of the corresponding GRID environment resources and services at different layers of networking abstraction. The relevance of the optimization topic is ensured by the fact that with increasing data flow intensi- ty, the latency of the various linear algorithm based subsystems as well increases. This leads to the general ef- fects, such as unacceptably high transmission time and processing instability. Logically paper can be divided into three parts with summary. The first part provides definition of TRIE and asymptotic estimates of corresponding algorithms (searching, deletion, insertion). The second part is devoted to the problem of routing time reduction by applying TRIE data structure. In particular, we analyze Cisco IOS switching services based on Bitwise TRIE and 256 way TRIE data structures. The third part contains general BOINC architecture review and recommenda- tions for highly-loaded projects. -

CS 106X, Lecture 21 Tries; Graphs
CS 106X, Lecture 21 Tries; Graphs reading: Programming Abstractions in C++, Chapter 18 This document is copyright (C) Stanford Computer Science and Nick Troccoli, licensed under Creative Commons Attribution 2.5 License. All rights reserved. Based on slides created by Keith Schwarz, Julie Zelenski, Jerry Cain, Eric Roberts, Mehran Sahami, Stuart Reges, Cynthia Lee, Marty Stepp, Ashley Taylor and others. Plan For Today • Tries • Announcements • Graphs • Implementing a Graph • Representing Data with Graphs 2 Plan For Today • Tries • Announcements • Graphs • Implementing a Graph • Representing Data with Graphs 3 The Lexicon • Lexicons are good for storing words – contains – containsPrefix – add 4 The Lexicon root the art we all arts you artsy 5 The Lexicon root the contains? art we containsPrefix? add? all arts you artsy 6 The Lexicon S T A R T L I N G S T A R T 7 The Lexicon • We want to model a set of words as a tree of some kind • The tree should be sorted in some way for efficient lookup • The tree should take advantage of words containing each other to save space and time 8 Tries trie ("try"): A tree structure optimized for "prefix" searches struct TrieNode { bool isWord; TrieNode* children[26]; // depends on the alphabet }; 9 Tries isWord: false a b c d e … “” isWord: true a b c d e … “a” isWord: false a b c d e … “ac” isWord: true a b c d e … “ace” 10 Reading Words Yellow = word in the trie A E H S / A E H S A E H S A E H S / / / / / / / / A E H S A E H S A E H S A E H S / / / / / / / / / / / / A E H S A E H S A E H S / / / / / / / -

Graph Traversals
Graph Traversals CS200 - Graphs 1 Tree traversal reminder Pre order A A B D G H C E F I In order B C G D H B A E C F I Post order D E F G H D B E I F C A Level order G H I A B C D E F G H I Connected Components n The connected component of a node s is the largest set of nodes reachable from s. A generic algorithm for creating connected component(s): R = {s} while ∃edge(u, v) : u ∈ R∧v ∉ R add v to R n Upon termination, R is the connected component containing s. q Breadth First Search (BFS): explore in order of distance from s. q Depth First Search (DFS): explores edges from the most recently discovered node; backtracks when reaching a dead- end. 3 Graph Traversals – Depth First Search n Depth First Search starting at u DFS(u): mark u as visited and add u to R for each edge (u,v) : if v is not marked visited : DFS(v) CS200 - Graphs 4 Depth First Search A B C D E F G H I J K L M N O P CS200 - Graphs 5 Question n What determines the order in which DFS visits nodes? n The order in which a node picks its outgoing edges CS200 - Graphs 6 DepthGraph Traversalfirst search algorithm Depth First Search (DFS) dfs(in v:Vertex) mark v as visited for (each unvisited vertex u adjacent to v) dfs(u) n Need to track visited nodes n Order of visiting nodes is not completely specified q if nodes have priority, then the order may become deterministic for (each unvisited vertex u adjacent to v in priority order) n DFS applies to both directed and undirected graphs n Which graph implementation is suitable? CS200 - Graphs 7 Iterative DFS: explicit Stack dfs(in v:Vertex) s – stack for keeping track of active vertices s.push(v) mark v as visited while (!s.isEmpty()) { if (no unvisited vertices adjacent to the vertex on top of the stack) { s.pop() //backtrack else { select unvisited vertex u adjacent to vertex on top of the stack s.push(u) mark u as visited } } CS200 - Graphs 8 Breadth First Search (BFS) n Is like level order in trees A B C D n Which is a BFS traversal starting E F G H from A? A. -

Tree-Combined Trie: a Compressed Data Structure for Fast IP Address Lookup
(IJACSA) International Journal of Advanced Computer Science and Applications, Vol. 6, No. 12, 2015 Tree-Combined Trie: A Compressed Data Structure for Fast IP Address Lookup Muhammad Tahir Shakil Ahmed Department of Computer Engineering, Department of Computer Engineering, Sir Syed University of Engineering and Technology, Sir Syed University of Engineering and Technology, Karachi Karachi Abstract—For meeting the requirements of the high-speed impact their forwarding capacity. In order to resolve two main Internet and satisfying the Internet users, building fast routers issues there are two possible solutions one is IPv6 IP with high-speed IP address lookup engine is inevitable. addressing scheme and second is Classless Inter-domain Regarding the unpredictable variations occurred in the Routing or CIDR. forwarding information during the time and space, the IP lookup algorithm should be able to customize itself with temporal and Finding a high-speed, memory-efficient and scalable IP spatial conditions. This paper proposes a new dynamic data address lookup method has been a great challenge especially structure for fast IP address lookup. This novel data structure is in the last decade (i.e. after introducing Classless Inter- a dynamic mixture of trees and tries which is called Tree- Domain Routing, CIDR, in 1994). In this paper, we will Combined Trie or simply TC-Trie. Binary sorted trees are more discuss only CIDR. In addition to these desirable features, advantageous than tries for representing a sparse population reconfigurability is also of great importance; true because while multibit tries have better performance than trees when a different points of this huge heterogeneous structure of population is dense. -

Balanced Trees Part One
Balanced Trees Part One Balanced Trees ● Balanced search trees are among the most useful and versatile data structures. ● Many programming languages ship with a balanced tree library. ● C++: std::map / std::set ● Java: TreeMap / TreeSet ● Many advanced data structures are layered on top of balanced trees. ● We’ll see several later in the quarter! Where We're Going ● B-Trees (Today) ● A simple type of balanced tree developed for block storage. ● Red/Black Trees (Today/Thursday) ● The canonical balanced binary search tree. ● Augmented Search Trees (Thursday) ● Adding extra information to balanced trees to supercharge the data structure. Outline for Today ● BST Review ● Refresher on basic BST concepts and runtimes. ● Overview of Red/Black Trees ● What we're building toward. ● B-Trees and 2-3-4 Trees ● Simple balanced trees, in depth. ● Intuiting Red/Black Trees ● A much better feel for red/black trees. A Quick BST Review Binary Search Trees ● A binary search tree is a binary tree with 9 the following properties: 5 13 ● Each node in the BST stores a key, and 1 6 10 14 optionally, some auxiliary information. 3 7 11 15 ● The key of every node in a BST is strictly greater than all keys 2 4 8 12 to its left and strictly smaller than all keys to its right. Binary Search Trees ● The height of a binary search tree is the 9 length of the longest path from the root to a 5 13 leaf, measured in the number of edges. 1 6 10 14 ● A tree with one node has height 0. -

Trees: Binary Search Trees
COMP2012H Spring 2014 Dekai Wu Binary Trees & Binary Search Trees (data structures for the dictionary ADT) Outline } Binary tree terminology } Tree traversals: preorder, inorder and postorder } Dictionary and binary search tree } Binary search tree operations } Search } min and max } Successor } Insertion } Deletion } Tree balancing issue COMP2012H (BST) Binary Tree Terminology } Go to the supplementary notes COMP2012H (BST) Linked Representation of Binary Trees } The degree of a node is the number of children it has. The degree of a tree is the maximum of its element degree. } In a binary tree, the tree degree is two data } Each node has two links left right } one to the left child of the node } one to the right child of the node Left child Right child } if no child node exists for a node, the link is set to NULL root 32 32 79 42 79 42 / 13 95 16 13 95 16 / / / / / / COMP2012H (BST) Binary Trees as Recursive Data Structures } A binary tree is either empty … Anchor or } Consists of a node called the root } Root points to two disjoint binary (sub)trees Inductive step left and right (sub)tree r left right subtree subtree COMP2012H (BST) Tree Traversal is Also Recursive (Preorder example) If the binary tree is empty then Anchor do nothing Else N: Visit the root, process data L: Traverse the left subtree Inductive/Recursive step R: Traverse the right subtree COMP2012H (BST) 3 Types of Tree Traversal } If the pointer to the node is not NULL: } Preorder: Node, Left subtree, Right subtree } Inorder: Left subtree, Node, Right subtree Inductive/Recursive step } Postorder: Left subtree, Right subtree, Node template <class T> void BinaryTree<T>::InOrder( void(*Visit)(BinaryTreeNode<T> *u), template<class T> BinaryTreeNode<T> *t) void BinaryTree<T>::PreOrder( {// Inorder traversal. -

Q-Tree: a Multi-Attribute Based Range Query Solution for Tele-Immersive Framework
Q-Tree: A Multi-Attribute Based Range Query Solution for Tele-Immersive Framework Md Ahsan Arefin, Md Yusuf Sarwar Uddin, Indranil Gupta, Klara Nahrstedt Department of Computer Science University of Illinois at Urbana Champaign Illinois, USA {marefin2, mduddin2, indy, klara}@illinois.edu Abstract given in a high level description which are transformed into multi-attribute composite range queries. Some of the Users and administrators of large distributed systems are examples include “which site is highly congested?”, “which frequently in need of monitoring and management of its components are not working properly?” etc. To answer the various components, data items and resources. Though there first one, the query is transformed into a multi-attribute exist several distributed query and aggregation systems, the composite range query with constrains (range of values) on clustered structure of tele-immersive interactive frameworks CPU utilization, memory overhead, stream rate, bandwidth and their time-sensitive nature and application requirements utilization, delay and packet loss rate. The later one can represent a new class of systems which poses different chal- be answered by constructing a multi-attribute range query lenges on this distributed search. Multi-attribute composite with constrains on static and dynamic characteristics of range queries are one of the key features in this class. those components. Queries can also be made by defining Queries are given in high level descriptions and then trans- different multi-attribute ranges explicitly. Another mention- formed into multi-attribute composite range queries. Design- able property of such systems is that the number of site is ing such a query engine with minimum traffic overhead, low limited due to limited display space and limited interactions, service latency, and with static and dynamic nature of large but the number of data items to store and manage can datasets, is a challenging task. -

Introduction to Linked List: Review
Introduction to Linked List: Review Source: http://www.geeksforgeeks.org/data-structures/linked-list/ Linked List • Fundamental data structures in C • Like arrays, linked list is a linear data structure • Unlike arrays, linked list elements are not stored at contiguous location, the elements are linked using pointers Array vs Linked List Why Linked List-1 • Advantages over arrays • Dynamic size • Ease of insertion or deletion • Inserting a new element in an array of elements is expensive, because room has to be created for the new elements and to create room existing elements have to be shifted For example, in a system if we maintain a sorted list of IDs in an array id[]. id[] = [1000, 1010, 1050, 2000, 2040] If we want to insert a new ID 1005, then to maintain the sorted order, we have to move all the elements after 1000 • Deletion is also expensive with arrays until unless some special techniques are used. For example, to delete 1010 in id[], everything after 1010 has to be moved Why Linked List-2 • Drawbacks of Linked List • Random access is not allowed. • Need to access elements sequentially starting from the first node. So we cannot do binary search with linked lists • Extra memory space for a pointer is required with each element of the list Representation in C • A linked list is represented by a pointer to the first node of the linked list • The first node is called head • If the linked list is empty, then the value of head is null • Each node in a list consists of at least two parts 1. -

Heaps a Heap Is a Complete Binary Tree. a Max-Heap Is A
Heaps Heaps 1 A heap is a complete binary tree. A max-heap is a complete binary tree in which the value in each internal node is greater than or equal to the values in the children of that node. A min-heap is defined similarly. 97 Mapping the elements of 93 84 a heap into an array is trivial: if a node is stored at 90 79 83 81 index k, then its left child is stored at index 42 55 73 21 83 2k+1 and its right child at index 2k+2 01234567891011 97 93 84 90 79 83 81 42 55 73 21 83 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Building a Heap Heaps 2 The fact that a heap is a complete binary tree allows it to be efficiently represented using a simple array. Given an array of N values, a heap containing those values can be built, in situ, by simply “sifting” each internal node down to its proper location: - start with the last 73 73 internal node * - swap the current 74 81 74 * 93 internal node with its larger child, if 79 90 93 79 90 81 necessary - then follow the swapped node down 73 * 93 - continue until all * internal nodes are 90 93 90 73 done 79 74 81 79 74 81 CS@VT Data Structures & Algorithms ©2000-2009 McQuain Heap Class Interface Heaps 3 We will consider a somewhat minimal maxheap class: public class BinaryHeap<T extends Comparable<? super T>> { private static final int DEFCAP = 10; // default array size private int size; // # elems in array private T [] elems; // array of elems public BinaryHeap() { . -

University of Cape Town Declaration
The copyright of this thesis vests in the author. No quotation from it or information derived from it is to be published without full acknowledgementTown of the source. The thesis is to be used for private study or non- commercial research purposes only. Cape Published by the University ofof Cape Town (UCT) in terms of the non-exclusive license granted to UCT by the author. University Automated Gateware Discovery Using Open Firmware Shanly Rajan Supervisor: Prof. M.R. Inggs Co-supervisor: Dr M. Welz University of Cape Town Declaration I understand the meaning of plagiarism and declare that all work in the dissertation, save for that which is properly acknowledged, is my own. It is being submitted for the degree of Master of Science in Engineering in the University of Cape Town. It has not been submitted before for any degree or examination in any other university. Signature of Author . Cape Town South Africa May 12, 2013 University of Cape Town i Abstract This dissertation describes the design and implementation of a mechanism that automates gateware1 device detection for reconfigurable hardware. The research facilitates the pro- cess of identifying and operating on gateware images by extending the existing infrastruc- ture of probing devices in traditional software by using the chosen technology. An automated gateware detection mechanism was devised in an effort to build a software system with the goal to improve performance and reduce software development time spent on operating gateware pieces by reusing existing device drivers in the framework of the chosen technology. This dissertation first investigates the system design to see how each of the user specifica- tions set for the KAT (Karoo Array Telescope) project in [28] could be achieved in terms of design decisions, toolchain selection and software modifications. -
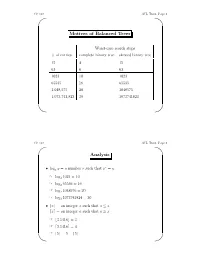
AVL Trees, Page 1 ' $
CS 310 AVL Trees, Page 1 ' $ Motives of Balanced Trees Worst-case search steps #ofentries complete binary tree skewed binary tree 15 4 15 63 6 63 1023 10 1023 65535 16 65535 1,048,575 20 1048575 1,073,741,823 30 1073741823 & % CS 310 AVL Trees, Page 2 ' $ Analysis r • logx y =anumberr such that x = y ☞ log2 1024 = 10 ☞ log2 65536 = 16 ☞ log2 1048576 = 20 ☞ log2 1073741824 = 30 •bxc = an integer a such that a ≤ x dxe = an integer a such that a ≥ x ☞ b3.1416c =3 ☞ d3.1416e =4 ☞ b5c =5=d5e & % CS 310 AVL Trees, Page 3 ' $ • If a binary search tree of N nodes happens to be complete, then a search in the tree requires at most b c log2 N +1 steps. • Big-O notation: We say f(x)=O(g(x)) if f(x)isbounded by c · g(x), where c is a constant, for sufficiently large x. ☞ x2 +11x − 30 = O(x2) (consider c =2,x ≥ 6) ☞ x100 + x50 +2x = O(2x) • If a BST happens to be complete, then a search in the tree requires O(log2 N)steps. • In a linked list of N nodes, a search requires O(N)steps. & % CS 310 AVL Trees, Page 4 ' $ AVL Trees • A balanced binary search tree structure proposed by Adelson, Velksii and Landis in 1962. • In an AVL tree of N nodes, every searching, deletion or insertion operation requires only O(log2 N)steps. • AVL tree searching is exactly the same as that of the binary search tree. & % CS 310 AVL Trees, Page 5 ' $ Definition • An empty tree is balanced. -

Binary Search Tree
ADT Binary Search Tree! Ellen Walker! CPSC 201 Data Structures! Hiram College! Binary Search Tree! •" Value-based storage of information! –" Data is stored in order! –" Data can be retrieved by value efficiently! •" Is a binary tree! –" Everything in left subtree is < root! –" Everything in right subtree is >root! –" Both left and right subtrees are also BST#s! Operations on BST! •" Some can be inherited from binary tree! –" Constructor (for empty tree)! –" Inorder, Preorder, and Postorder traversal! •" Some must be defined ! –" Insert item! –" Delete item! –" Retrieve item! The Node<E> Class! •" Just as for a linked list, a node consists of a data part and links to successor nodes! •" The data part is a reference to type E! •" A binary tree node must have links to both its left and right subtrees! The BinaryTree<E> Class! The BinaryTree<E> Class (continued)! Overview of a Binary Search Tree! •" Binary search tree definition! –" A set of nodes T is a binary search tree if either of the following is true! •" T is empty! •" Its root has two subtrees such that each is a binary search tree and the value in the root is greater than all values of the left subtree but less than all values in the right subtree! Overview of a Binary Search Tree (continued)! Searching a Binary Tree! Class TreeSet and Interface Search Tree! BinarySearchTree Class! BST Algorithms! •" Search! •" Insert! •" Delete! •" Print values in order! –" We already know this, it#s inorder traversal! –" That#s why it#s called “in order”! Searching the Binary Tree! •" If the tree is