Implicit Differentiation and the Second Derivative
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Mean Value Theorem Math 120 Calculus I Fall 2015
The Mean Value Theorem Math 120 Calculus I Fall 2015 The central theorem to much of differential calculus is the Mean Value Theorem, which we'll abbreviate MVT. It is the theoretical tool used to study the first and second derivatives. There is a nice logical sequence of connections here. It starts with the Extreme Value Theorem (EVT) that we looked at earlier when we studied the concept of continuity. It says that any function that is continuous on a closed interval takes on a maximum and a minimum value. A technical lemma. We begin our study with a technical lemma that allows us to relate 0 the derivative of a function at a point to values of the function nearby. Specifically, if f (x0) is positive, then for x nearby but smaller than x0 the values f(x) will be less than f(x0), but for x nearby but larger than x0, the values of f(x) will be larger than f(x0). This says something like f is an increasing function near x0, but not quite. An analogous statement 0 holds when f (x0) is negative. Proof. The proof of this lemma involves the definition of derivative and the definition of limits, but none of the proofs for the rest of the theorems here require that depth. 0 Suppose that f (x0) = p, some positive number. That means that f(x) − f(x ) lim 0 = p: x!x0 x − x0 f(x) − f(x0) So you can make arbitrarily close to p by taking x sufficiently close to x0. -

AP Calculus AB Topic List 1. Limits Algebraically 2. Limits Graphically 3
AP Calculus AB Topic List 1. Limits algebraically 2. Limits graphically 3. Limits at infinity 4. Asymptotes 5. Continuity 6. Intermediate value theorem 7. Differentiability 8. Limit definition of a derivative 9. Average rate of change (approximate slope) 10. Tangent lines 11. Derivatives rules and special functions 12. Chain Rule 13. Application of chain rule 14. Derivatives of generic functions using chain rule 15. Implicit differentiation 16. Related rates 17. Derivatives of inverses 18. Logarithmic differentiation 19. Determine function behavior (increasing, decreasing, concavity) given a function 20. Determine function behavior (increasing, decreasing, concavity) given a derivative graph 21. Interpret first and second derivative values in a table 22. Determining if tangent line approximations are over or under estimates 23. Finding critical points and determining if they are relative maximum, relative minimum, or neither 24. Second derivative test for relative maximum or minimum 25. Finding inflection points 26. Finding and justifying critical points from a derivative graph 27. Absolute maximum and minimum 28. Application of maximum and minimum 29. Motion derivatives 30. Vertical motion 31. Mean value theorem 32. Approximating area with rectangles and trapezoids given a function 33. Approximating area with rectangles and trapezoids given a table of values 34. Determining if area approximations are over or under estimates 35. Finding definite integrals graphically 36. Finding definite integrals using given integral values 37. Indefinite integrals with power rule or special derivatives 38. Integration with u-substitution 39. Evaluating definite integrals 40. Definite integrals with u-substitution 41. Solving initial value problems (separable differential equations) 42. Creating a slope field 43. -

Multivariable and Vector Calculus
Multivariable and Vector Calculus Lecture Notes for MATH 0200 (Spring 2015) Frederick Tsz-Ho Fong Department of Mathematics Brown University Contents 1 Three-Dimensional Space ....................................5 1.1 Rectangular Coordinates in R3 5 1.2 Dot Product7 1.3 Cross Product9 1.4 Lines and Planes 11 1.5 Parametric Curves 13 2 Partial Differentiations ....................................... 19 2.1 Functions of Several Variables 19 2.2 Partial Derivatives 22 2.3 Chain Rule 26 2.4 Directional Derivatives 30 2.5 Tangent Planes 34 2.6 Local Extrema 36 2.7 Lagrange’s Multiplier 41 2.8 Optimizations 46 3 Multiple Integrations ........................................ 49 3.1 Double Integrals in Rectangular Coordinates 49 3.2 Fubini’s Theorem for General Regions 53 3.3 Double Integrals in Polar Coordinates 57 3.4 Triple Integrals in Rectangular Coordinates 62 3.5 Triple Integrals in Cylindrical Coordinates 67 3.6 Triple Integrals in Spherical Coordinates 70 4 Vector Calculus ............................................ 75 4.1 Vector Fields on R2 and R3 75 4.2 Line Integrals of Vector Fields 83 4.3 Conservative Vector Fields 88 4.4 Green’s Theorem 98 4.5 Parametric Surfaces 105 4.6 Stokes’ Theorem 120 4.7 Divergence Theorem 127 5 Topics in Physics and Engineering .......................... 133 5.1 Coulomb’s Law 133 5.2 Introduction to Maxwell’s Equations 137 5.3 Heat Diffusion 141 5.4 Dirac Delta Functions 144 1 — Three-Dimensional Space 1.1 Rectangular Coordinates in R3 Throughout the course, we will use an ordered triple (x, y, z) to represent a point in the three dimensional space. -
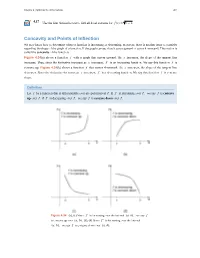
Concavity and Points of Inflection We Now Know How to Determine Where a Function Is Increasing Or Decreasing
Chapter 4 | Applications of Derivatives 401 4.17 3 Use the first derivative test to find all local extrema for f (x) = x − 1. Concavity and Points of Inflection We now know how to determine where a function is increasing or decreasing. However, there is another issue to consider regarding the shape of the graph of a function. If the graph curves, does it curve upward or curve downward? This notion is called the concavity of the function. Figure 4.34(a) shows a function f with a graph that curves upward. As x increases, the slope of the tangent line increases. Thus, since the derivative increases as x increases, f ′ is an increasing function. We say this function f is concave up. Figure 4.34(b) shows a function f that curves downward. As x increases, the slope of the tangent line decreases. Since the derivative decreases as x increases, f ′ is a decreasing function. We say this function f is concave down. Definition Let f be a function that is differentiable over an open interval I. If f ′ is increasing over I, we say f is concave up over I. If f ′ is decreasing over I, we say f is concave down over I. Figure 4.34 (a), (c) Since f ′ is increasing over the interval (a, b), we say f is concave up over (a, b). (b), (d) Since f ′ is decreasing over the interval (a, b), we say f is concave down over (a, b). 402 Chapter 4 | Applications of Derivatives In general, without having the graph of a function f , how can we determine its concavity? By definition, a function f is concave up if f ′ is increasing. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

Matrix Calculus
Appendix D Matrix Calculus From too much study, and from extreme passion, cometh madnesse. Isaac Newton [205, §5] − D.1 Gradient, Directional derivative, Taylor series D.1.1 Gradients Gradient of a differentiable real function f(x) : RK R with respect to its vector argument is defined uniquely in terms of partial derivatives→ ∂f(x) ∂x1 ∂f(x) , ∂x2 RK f(x) . (2053) ∇ . ∈ . ∂f(x) ∂xK while the second-order gradient of the twice differentiable real function with respect to its vector argument is traditionally called the Hessian; 2 2 2 ∂ f(x) ∂ f(x) ∂ f(x) 2 ∂x1 ∂x1∂x2 ··· ∂x1∂xK 2 2 2 ∂ f(x) ∂ f(x) ∂ f(x) 2 2 K f(x) , ∂x2∂x1 ∂x2 ··· ∂x2∂xK S (2054) ∇ . ∈ . .. 2 2 2 ∂ f(x) ∂ f(x) ∂ f(x) 2 ∂xK ∂x1 ∂xK ∂x2 ∂x ··· K interpreted ∂f(x) ∂f(x) 2 ∂ ∂ 2 ∂ f(x) ∂x1 ∂x2 ∂ f(x) = = = (2055) ∂x1∂x2 ³∂x2 ´ ³∂x1 ´ ∂x2∂x1 Dattorro, Convex Optimization Euclidean Distance Geometry, Mεβoo, 2005, v2020.02.29. 599 600 APPENDIX D. MATRIX CALCULUS The gradient of vector-valued function v(x) : R RN on real domain is a row vector → v(x) , ∂v1(x) ∂v2(x) ∂vN (x) RN (2056) ∇ ∂x ∂x ··· ∂x ∈ h i while the second-order gradient is 2 2 2 2 , ∂ v1(x) ∂ v2(x) ∂ vN (x) RN v(x) 2 2 2 (2057) ∇ ∂x ∂x ··· ∂x ∈ h i Gradient of vector-valued function h(x) : RK RN on vector domain is → ∂h1(x) ∂h2(x) ∂hN (x) ∂x1 ∂x1 ··· ∂x1 ∂h1(x) ∂h2(x) ∂hN (x) h(x) , ∂x2 ∂x2 ··· ∂x2 ∇ . -

440 Geophysics: Brief Notes on Math Thorsten Becker, University of Southern California, 02/2005
440 Geophysics: Brief notes on math Thorsten Becker, University of Southern California, 02/2005 Linear algebra Linear (vector) algebra is discussed in the appendix of Fowler and in your favorite math textbook. I only make brief comments here, to clarify and summarize a few issues that came up in class. At places, these are not necessarily mathematically rigorous. Dot product We have made use of the dot product, which is defined as n c =~a ·~b = ∑ aibi, (1) i=1 where ~a and~b are vectors of dimension n (n-dimensional, pointed objects like a velocity) and the n outcome of this operation is a scalar (a regular number), c. In eq. (1), ∑i=1 means “sum all that follows while increasing the index i from the lower limit, i = 1, in steps of of unity, to the upper limit, i = n”. In the examples below, we will assume a typical, spatial coordinate system with n = 3 so that ~a ·~b = a1b1 + a2b2 + a3b3, (2) where 1, 2, 3 refer to the vectors components along x, y, and z axis, respectively. When we write out the vector components, we put them on top of each other a1 ax ~a = a2 = ay (3) a3 az or in a list, maybe with curly brackets, like so: ~a = {a1,a2,a3}. On the board, I usually write vectors as a rather than ~a, because that’s easier. You may also see vectors printed as bold face letters, like so: a. We can write the amplitude or length of a vector as s n q q 2 2 2 2 2 2 2 |~a| = ∑ai = a1 + a2 + a3 = ax + ay + az . -

3.4 AP Calculus Concavity and the Second Derivative.Notebook November 07, 2016
3.4 AP Calculus Concavity and the second derivative.notebook November 07, 2016 3.4 Concavity & The Second Derivative Learning Targets 1. Determine intervals on which a function is concave upward or concave downward 2. Find inflection points of a function. 3. Find relative extrema of a function using Second Derivative Test. *no make‐up Monday today Intro/Warmup 1 3.4 AP Calculus Concavity and the second derivative.notebook November 07, 2016 Nov 78:41 AM 2 3.4 AP Calculus Concavity and the second derivative.notebook November 07, 2016 ∫ Concave Upward or Concave Downward If f' is increasing on an interval, then the function is concave upward on that interval If f' is decreasing on an interval, then the function is concave downward on that interval. note: concave upward means the graph lies above its tangent lines, and concave downwards means the graph lies below its tangent lines. I.concave upward or concave downward 3 3.4 AP Calculus Concavity and the second derivative.notebook November 07, 2016 ∫ Concave Upward or Concave Downward continued Test For Concavity: Let f be a function whose second derivative exists on an open interval I. 1. If f''(x) > 0 for all x in I, then the graph of f is concave upward on I. 2. If f''(x) < 0 for all x in I, then the graph of f is concave downward on I. 1. Determine the open intervals on which the graph of is concave upward or downward. I.Concave Upward or Downward cont 4 3.4 AP Calculus Concavity and the second derivative.notebook November 07, 2016 ∫∫∫ Second Derivative Test Second Derivative Test Let f be a function such that f'(c) = 0 and the second derivative of f exists on an open interval containing c. -

Calculus Online Textbook Chapter 2
Contents CHAPTER 1 Introduction to Calculus 1.1 Velocity and Distance 1.2 Calculus Without Limits 1.3 The Velocity at an Instant 1.4 Circular Motion 1.5 A Review of Trigonometry 1.6 A Thousand Points of Light 1.7 Computing in Calculus CHAPTER 2 Derivatives The Derivative of a Function Powers and Polynomials The Slope and the Tangent Line Derivative of the Sine and Cosine The Product and Quotient and Power Rules Limits Continuous Functions CHAPTER 3 Applications of the Derivative 3.1 Linear Approximation 3.2 Maximum and Minimum Problems 3.3 Second Derivatives: Minimum vs. Maximum 3.4 Graphs 3.5 Ellipses, Parabolas, and Hyperbolas 3.6 Iterations x, + ,= F(x,) 3.7 Newton's Method and Chaos 3.8 The Mean Value Theorem and l'H8pital's Rule CHAPTER 2 Derivatives 2.1 The Derivative of a Function This chapter begins with the definition of the derivative. Two examples were in Chapter 1. When the distance is t2, the velocity is 2t. When f(t) = sin t we found v(t)= cos t. The velocity is now called the derivative off (t). As we move to a more formal definition and new examples, we use new symbols f' and dfldt for the derivative. 2A At time t, the derivativef'(t)or df /dt or v(t) is fCt -t At) -f (0 f'(t)= lim (1) At+O At The ratio on the right is the average velocity over a short time At. The derivative, on the left side, is its limit as the step At (delta t) approaches zero. -

Lecture 3: Derivatives in Rn 1 Definitions and Concepts
Math 94 Professor: Padraic Bartlett Lecture 3: Derivatives in Rn Week 3 UCSB 2015 This is the third week of the Mathematics Subject Test GRE prep course; here, we review the concepts of derivatives in higher dimensions! 1 Definitions and Concepts n We start by reviewing the definitions we have for the derivative of functions on R : Definition. The partial derivative @f of a function f : n ! along its i-th co¨ordinate @xi R R at some point a, formally speaking, is the limit f(a + h · e ) − f(a) lim i : h!0 h (Here, ei is the i-th basis vector, which has its i-th co¨ordinateequal to 1 and the rest equal to 0.) However, this is not necessarily the best way to think about the partial derivative, and certainly not the easiest way to calculate it! Typically, we think of the i-th partial derivative of f as the derivative of f when we \hold all of f's other variables constant" { i.e. if we think of f as a single-variable function with variable xi, and treat all of the other xj's as constants. This method is markedly easier to work with, and is how we actually *calculate* a partial derivative. n We can extend this to higher-order derivatives as follows. Given a function f : R ! R, we can define its second-order partial derivatives as the following: @2f @ @f = : @xi@xj @xi @xj In other words, the second-order partial derivatives are simply all of the functions you can get by taking two consecutive partial derivatives of your function f. -

Appendix: TABLE of INTEGRALS
-~.I-- Appendix: TABLE OF INTEGRALS 148. In the following table, the constant of integration, C, is omitted but should be added to the result of every integration. The letter x represents any variable; u represents any function of x; the remaining letters represent arbitrary constants, unless otherwise indicated; all angles are in radians. Unless otherwise mentioned, loge u = log u. Expressions Containing ax + b 1. I(ax+ b)ndx= 1 (ax+ b)n+l, n=l=-1. a(n + 1) dx 1 2. = -loge<ax + b). Iax+ b a 3 I dx =_ 1 • (ax+b)2 a(ax+b)· 4 I dx =_ 1 • (ax + b)3 2a(ax + b)2· 5. Ix(ax + b)n dx = 1 (ax + b)n+2 a2 (n + 2) b ---,,---(ax + b)n+l n =1= -1, -2. a2 (n + 1) , xdx x b 6. = - - -2 log(ax + b). I ax+ b a a 7 I xdx = b 1 I ( b) • (ax + b)2 a2(ax + b) + -;}i og ax + . 369 370 • Appendix: Table of Integrals 8 I xdx = b _ 1 • (ax + b)3 2a2(ax + b)2 a2(ax + b) . 1 (ax+ b)n+3 (ax+ b)n+2 9. x2(ax + b)n dx = - - 2b--'------'-- I a2 n + 3 n + 2 2 b (ax + b) n+ 1 ) + , ni=-I,-2,-3. n+l 2 10. I x dx = ~ (.!..(ax + b)2 - 2b(ax + b) + b2 10g(ax + b)). ax+ b a 2 2 2 11. I x dx 2 =~(ax+ b) - 2blog(ax+ b) _ b ). (ax + b) a ax + b 2 2 12 I x dx = _1(10 (ax + b) + 2b _ b ) • (ax + b) 3 a3 g ax + b 2(ax + b) 2 . -

Numerical Computation of Second Derivatives with Applications
Numerical Computation of Second Derivatives 1 with Applications to Optimization Problems Philip Caplan – [email protected] Abstract Newton’s method is applied to the minimization of a computationally expensive objective function. Various methods for computing the exact Hessian are examined, notably adjoint-based methods and the hyper-dual method. 2 The hyper-dual number method still requires O(N ) function evaluations to compute the exact Hessian during each optimization iteration. The adjoint-based methods all require O(N) evaluations. In particular, the fastest method is the direct-adjoint method as it requires N evaluations as opposed to the adjoint-adjoint and adjoint-direct methods which both require 2N evaluations. Applications to a boundary-value problem are presented. Index Terms Second derivative, Hessian, adjoint, direct, hyper-dual, optimization I. INTRODUCTION EWTON’S method is a powerful optimization algorithm which is well known to converge quadratically upon N the root of the gradient of a given objective function. The drawback of this method, however, is the calculation of the second derivative matrix of the objective function, or Hessian. When the objective function is computationally expensive to evaluate, the adjoint method is suitable to compute its gradient. Such expensive function evaluations may, for example, depend on some nonlinear partial differential equation such as those enountered in aerodynamics [7], [12]. With this gradient information, steepest-descent or conjugate-gradient algorithms can then be applied to the optimization problem; however, convergence will often be slow [9]. Quasi-Newton methods will successively approximate the Hessian matrix with either Broyden-Fletcher-Goldfarb- Shanno (BFGS) or Davidon-Fletcher-Powell (DFP) updates [13] which can dramatically improve convergence.