Comparing Count-Based and Band-Based Indices of Word Frequency: Implications for Active Vocabulary Research and Pedagogical Applications
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Downloaded for Free
Salem State University From the SelectedWorks of Sovicheth Boun March 24, 2014 A Critical Examination Of Language Ideologies And Identities Of Cambodian Foreign-Trained University Lecturers Of English Sovicheth Boun Available at: https://works.bepress.com/sovicheth-boun/2/ Table of Contents General Conference Information ....................................................................................................................................................................... 3-‐13 Welcome Messages from the President and the Conference Chair ........................................................................................................................ 3 Conference Program Committee .......................................................................................................................................................................................... 4 Registration Information, Exhibit Hall Coffee Hours, Breaks, Internet Access, Conference Evaluation ................................................ 4 Strand Coordinators and Abstract Readers .................................................................................................................................................................. 5-‐6 Student Volunteers, Individual Sessions and Roundtable Sessions Instructions ............................................................................................ 7 Conference Sponsors ............................................................................................................................................................................................................. -

Language Education & Assessment the Effect of Cohesive Features In
OPEN ACCESS Language Education & Assessment ISSN 2209-3591 https://journals.castledown-publishers.com/lea/ Language Education & Assessment, 2 (3), 110-134 (2019) https://doi.org/10.29140/lea.v2n3.152 The Effect of Cohesive Features in Integrated and Independent L2 Writing Quality and Text Classification RURIK TYWONIW a SCOTT CROSSLEY b a Georgia State University, USA b Georgia State University, USA EmAil: [email protected] EmAil: [email protected] Abstract Cohesion feAtures were cAlculAted for A corpus of 960 essAys by 480 test-tAkers from the Test of English As A Foreign LAnguage (TOEFL) in order to examine differences in the use of cohesion devices between integrated (source-based) writing And independent writing sAmples. Cohesion indices were meAsured using An AutomAted textual Analysis tool, the Tool for the AutomAtic Assessment of Cohesion (TAACO). A discriminant function Analysis correctly clAssified essAys As either integrated or independent in 92.3 per cent of cAses. Integrated writing wAs mArked by higher use of specific connectives And greAter lexicAl overlAp of content words between textual units, whereAs independent writing wAs mArked by greAter lexicAl overlAp of function words, especiAlly pronouns. Regression Analyses found that cohesive indices which distinguish tAsks predict writing quality judgments more strongly in independent writing. However, the strongest predictor of humAn judgments wAs the sAme for both tAsks: lexicAl overlAp of function words. The findings demonstrate that text cohesion is A multidimensional construct shaped by the writing tAsk, yet the meAsures of cohesion which Affect humAn judgments of writing quality Are not entirely different Across tAsks. These Analyses Allow us to better understAnd cohesive feAtures in writing tAsks And implicAtions for AutomAted writing Assessment. -

Proceedings of the Workshop on Computational Linguistics for Linguistic Complexity, Pages 1–11, Osaka, Japan, December 11-17 2016
CL4LC 2016 Computational Linguistics for Linguistic Complexity Proceedings of the Workshop December 11, 2016 Osaka, Japan Copyright of each paper stays with the respective authors (or their employers). ISBN 978-4-87974-709-9 ii Preface Welcome to the first edition of the “Computational Linguistics for Linguistic Complexity” workshop (CL4LC)! CL4LC aims at investigating “processing” aspects of linguistic complexity with the objective of promoting a common reflection on approaches for the detection, evaluation and modelling of linguistic complexity. What has motivated such a focus on linguistic complexity? Although the topic of linguistic complexity has attracted researchers for quite some time, this concept is still poorly defined and often used with different meanings. Linguistic complexity indeed is inherently a multidimensional concept that must be approached from various perspectives, ranging from natural language processing (NLP), second language acquisition (SLA), psycholinguistics and cognitive science, as well as contrastive linguistics. In 2015, a one-day workshop dedicated to the question of Measuring Linguistic Complexity was organized at the catholic University of Louvain (UCL) with the aim of identifying convergent approaches in diverse fields addressing linguistic complexity from their specific viewpoint. Not only did the workshop turn out to be a great success, but it strikingly pointed out that more in–depth thought is required in order to investigate how research on linguistic complexity and its processing aspects could actually benefit from the sharing of definitions, methodologies and techniques developed from different perspectives. CL4LC stems from these reflections and would like to go a step further towards a more multifaceted view of linguistic complexity. In particular, the workshop would like to investigate processing aspects of linguistic complexity both from a machine point of view and from the perspective of the human subject in order to pinpoint possible differences and commonalities. -

Text Readability and Intuitive Simplification: a Comparison of Readability Formulas
Reading in a Foreign Language April 2011, Volume 23, No. 1 ISSN 1539-0578 pp. 84–101 Text readability and intuitive simplification: A comparison of readability formulas Scott A. Crossley Georgia State University United States David B. Allen University of Tokyo Japan Danielle S. McNamara University of Memphis United States Abstract Texts are routinely simplified for language learners with authors relying on a variety of approaches and materials to assist them in making the texts more comprehensible. Readability measures are one such tool that authors can use when evaluating text comprehensibility. This study compares the Coh-Metrix Second Language (L2) Reading Index, a readability formula based on psycholinguistic and cognitive models of reading, to traditional readability formulas on a large corpus of texts intuitively simplified for language learners. The goal of this study is to determine which formula best classifies text level (advanced, intermediate, beginner) with the prediction that text classification relates to the formulas’ capacity to measure text comprehensibility. The results demonstrate that the Coh-Metrix L2 Reading Index performs significantly better than traditional readability formulas, suggesting that the variables used in this index are more closely aligned to the intuitive text processing employed by authors when simplifying texts. Keywords: readability, Coh-Metrix L2 Reading Index, simplification, psycholinguistics, cognitive science, computational linguistics, corpus linguistics When materials developers want to simplify texts to provide more comprehensible input to second language (L2) learners, they generally have two approaches: a structural or an intuitive approach (Allen, 2009). A structural approach depends on the use of structure and word lists that are predefined by level, as typically found in graded readers. -
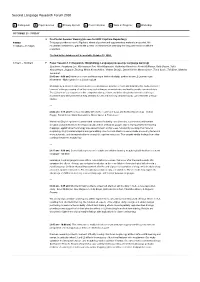
Second Language Research Forum 2020
Second Language Research Forum 2020 C Colloquium P Paper Session L Plenary Speech S Poster Session W Work-in-Progress R Workshop OCTOBER 23 • FRIDAY S Pre-Poster Session Viewing (Access to SLRF Figshare Repository) PINNED This page provides access to Figshare, where all posters and supplementary materials are posted. We 12:00am – 11:59pm recommend attendees to preview the posters of interest before attending the live poster sessions with the presenters. The link to the database will be available October 15, 2020. 8:45am – 10:00am P Paper Session 1.C (Keywords: Morphology, Language processing, Language learning) Speakers: Jongbong Lee, Myeongeun Son, Alex Magnuson, Katherine Kerschen, Kevin McManus, Kelly Bayas, Yulia Khoruzhaya, Jingyuan Zhuang, Maria Kostromitina, Vedran Dronjic, Daniel Keller, Maren Greve, Tiana Covic, Tali Bitan, Mathieu Lecouvet [8:45 am - 9:00 am] Attention to Form and Meaning in Written Modality: Evidence from L2 Learners’ Eye Movements - Myeongeun Son & Jongbong Lee Motivated by a series of replication studies on simultaneous attention to form and meaning, this study revisits L2 learners’ online processing of text by using eye-tracking as an unobtrusive method to provide concurrent data. The L2 learners’ (a) responses to the comprehension questions and (b) reading behaviors reflected in eye movement data demonstrate that they attended to form and meaning simultaneously, consistent with previous studies. --- [9:00 am - 9:15 am] How Input Variability Affects the Learning of Case and Number Morphology - Vedran Dronjic, Daniel Keller, Maria Kostromitina, Maren Greve & Tiana Covic We trained English speakers to understand sentences featuring case (inessive, superessive) and number (singular, plural) inflection in three typologically distinct artificial languages. -

Validity of a Computational Linguistics-Derived Automated Health Literacy Measure Across Race/Ethnicity: Findings from the ECLIPPSE Project
Validity of a Computational Linguistics-Derived Automated Health Literacy Measure Across Race/Ethnicity: Findings from The ECLIPPSE Project Dean Schillinger, Renu Balyan, Scott Crossley, Danielle McNamara, Andrew Karter Journal of Health Care for the Poor and Underserved, Volume 32, Number 2, May 2021 Supplement, pp. 347-365 (Article) Published by Johns Hopkins University Press DOI: https://doi.org/10.1353/hpu.2021.0067 For additional information about this article https://muse.jhu.edu/article/789674 [ Access provided at 27 Sep 2021 09:00 GMT with no institutional affiliation ] ORIGINAL PAPER Validity of a Computational Linguistics- Derived Automated Health Literacy Measure Across Race/ Ethnicity: Findings from The ECLIPPSE Project Dean Schillinger, MD Renu Balyan, PhD Scott Crossley, PhD Danielle McNamara, PhD Andrew Karter, PhD Abstract: Limited health literacy (HL) partially mediates health disparities. Measurement constraints, including lack of validity assessment across racial/ ethnic groups and admin- istration challenges, have undermined the field and impeded scaling of HL interventions. We employed computational linguistics to develop an automated and novel HL measure, analyzing >300,000 messages sent by >9,000 diabetes patients via a patient portal to create a Literacy Profiles. We carried out stratified analyses among White/non- Hispanics, Black/ non- Hispanics, Hispanics, and Asian/ Pacific Islanders to determine if the Literacy Profile has comparable criterion and predictive validities. We discovered that criterion validity was consistently high across all groups (c- statistics 0.82– 0.89). We observed consistent relation- ships across racial/ ethnic groups between HL and outcomes, including communication, adherence, hypoglycemia, diabetes control, and ED utilization. While concerns have arisen regarding bias in AI, the automated Literacy Profile appears sufficiently valid across race/ ethnicity, enabling HL measurement at a scale that could improve clinical care and popu- lation health among diverse populations. -

EMPIRICAL STUDY Particle Placement in Learner Language
Language Learning ISSN 0023-8333 EMPIRICAL STUDY Particle Placement in Learner Language Stefanie Wulff and Stefan Th. Gries University of Florida and University of California at Santa Barbara This study presents the first multifactorial corpus-based analysis of verb–particle con- structions in a data sample comprising spoken and written productions by intermediate- level learners of English as a second language from 17 language backgrounds. We annotated 4,911 attestations retrieved from native speaker and language learner corpora for 14 predictors, including syntactic complexity, rhythmic and segment alternation, and the verb framing of the speaker’s native language. A multifactorial prediction and deviation analysis using regression (Gries & Deshors, 2014), which stacks multiple regression analyses to compare native speaker and learner productions in identical con- texts, revealed a complex picture in which processing demands, input effects, and native language typology jointly shape the degree to which learners’ choices of constructions are nativelike or not. Keywords verb–particle construction; particle placement; learner corpus research; multifactorial regression; mixed-effects model; second language Introduction The acquisition of multiword units constitutes a challenging aspect of learning a language, be it a learner’s first language (L1) or second language (L2). One type of multiword unit in English is verb–particle constructions (VPCs; also called transitive phrasal verbs), that is, combinations of a verb and a particle such as pick up NP, take out NP, or throw away NP (where NP stands for a noun phrase). VPCs are particularly difficult to acquire for several reasons. For one, they, although ubiquitous in English, are not particularly frequent in non- Germanic languages, so many L2 learners of English do not benefit from having We are grateful to the three anonymous reviewers and to Associate Editor Scott Crossley for their helpful and insightful comments. -

Mouton De Gruyter | IRAL 49-1 (2011) | 1St Proofs Scott Crossley and Thomas Lee Salsbury / [email protected], [email protected]
Mouton de Gruyter | IRAL 49-1 (2011) | 1st proofs Scott Crossley and Thomas Lee Salsbury / [email protected], [email protected] The development of lexical bundle accuracy and production Please note: page- and linebreaks are temporary; overlong lines, orphans/widows, and split examples will be dealt with after your corrections have been incorporated; there is no need to mark split examples or bad page breaks. Typesetter’s notes/queries /1/ Article adapted to IRAL style sheet. There is a huge number of minor changes and corrections, please carefully check the file for errors. Preliminary page and line breaks 1-iral-49-1 — 2011/1/29 18:46—1— #2—ce Mouton de Gruyter The development of lexical bundle accuracy and production in English second language speakers SCOTT CROSSLEY AND THOMAS LEE SALSBURY Abstract Six adult, second language (L2) English learners were observed over a period of one year to explore the development of lexical bundles (i.e., bigrams) in nat- urally produced, oral English. Total bigrams produced by the L2 learners over the year of observation that were shared with native speakers were compared using a frequency index to explore L2 learner’s accuracy of use. The results of the study support the notion that bigram accuracy increases as a function of time spent learning English. This finding lends credence to the notion that the production of lexical bundles by L2 learners begins to develop in paral- lel with the frequency of lexical bundles used by native speakers. Like native speakers, L2 learners also begin to produce lexical bundles that serve prag- matic and syntactic functions. -
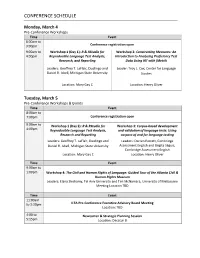
Conference Schedule
CONFERENCE SCHEDULE Monday, March 4 Pre-Conference Workshops Time Event 8:00am to 3:00pm Conference registration open 9:00am to Workshop 1 (Day 1): R & RStudio for Workshop 2: Constructing Measures: An 4:00pm Reproducible Language Test Analysis, Introduction to Analyzing Proficiency Test Research, and Reporting Data Using IRT with jMetrik Leaders: Geoffrey T. LaFlair, Duolingo and Leader: Troy L. Cox, Center for Language Daniel R. Isbell, Michigan State University Studies Location: Mary Gay C Location: Henry Oliver Tuesday, March 5 Pre-Conference Workshops & Events Time Event 8:00am to 7:00pm Conference registration open 9:00am to Workshop 1 (Day 2): R & RStudio for Workshop 3: Corpus-based development 4:00pm Reproducible Language Test Analysis, and validation of language tests: Using Research and Reporting corpora of and for language testing Leaders: Geoffrey T. LaFlair, Duolingo and Leaders: Darren Perrett, Cambridge Daniel R. Isbell, Michigan State University Assessment English and Brigita Séguis, Cambridge Assessment English Location: Mary Gay C Location: Henry Oliver Time Event 9:00am to 1:00pm Workshop 4: The Civil and Human Rights of Language: Guided Tour of the Atlanta Civil & Human Rights Museum Leaders: Elana Shohamy, Tel Aviv University and Tim McNamara, University of Melbourne Meeting Location TBD Time Event 11:00am to 3:30pm ILTA Pre-Conference Executive Advisory Board Meeting Location: TBD 4:00 to Newcomer & Strategic Planning Session 5:15pm Location: Decatur B CONFERENCE SCHEDULE Tuesday, March 5 Time Event 5:15 to Alan -

Assessing Writing with the Tool for the Automatic Analysis of Lexical Sophistication (TAALES) T ⁎ Scott A
Assessing Writing 38 (2018) 46–50 Contents lists available at ScienceDirect Assessing Writing journal homepage: www.elsevier.com/locate/asw Assessing writing with the tool for the automatic analysis of lexical sophistication (TAALES) T ⁎ Scott A. Crossleya, , Kristopher Kyleb a Department of Applied Linguistics/ESL, Georgia State University, 25 Park Place, Suite 1500, Atlanta, GA, 30303, USA b Department of Second Language Studies, University of Hawai’i Manoa, Moore Hall 570, 1890 East-West Road, Honolulu, 96822, Hawaii ARTICLE INFO ABSTRACT Keywords: Tool: Tool for the Automatic Analysis of Lexical Sophistication (TAALES). Lexical sophistication Tool Purpose: To calculate a wide range of classic and newly developed indices of lexical so- Natural language processing phistication (e.g., frequency, range, academic register, concreteness and familiarity, psycho- Automatic writing assessment linguistic word properties, and semantic network norms). Key Premise: Lexical sophistication features are strong predictors of writing quality in both first language (L1) and second language (L2) contexts. Research Connections: Inspired by Coh-Metrix but developed to improve on the limitations of the Coh-Metric tool. Limitations: Does not examine accuracy of lexical use or words not available in selected data- bases. Future Developments: Continue to add lexical databases as they become available. 1. Introduction In this review, we provide an overview of the Tool for the Automatic Analysis of Lexical Sophistication (TAALES; Kyle & Crossley, 2015; Kyle, Crossley, & Berger, 2017) and discuss its applications for automatically assessing features of written text. TAALES is a is context and learner independent natural language processing (NLP) tool that provides counts for 100 s of lexical features. -
![Arxiv:2105.09653V1 [Cs.CL] 20 May 2021 on These Dimensions](https://docslib.b-cdn.net/cover/5978/arxiv-2105-09653v1-cs-cl-20-may-2021-on-these-dimensions-2925978.webp)
Arxiv:2105.09653V1 [Cs.CL] 20 May 2021 on These Dimensions
LAST at SemEval-2021 Task 1: Improving Multi-Word Complexity Prediction Using Bigram Association Measures Yves Bestgen Laboratoire d’analyse statistique des textes - LAST Institut de recherche en sciences psychologiques Universite´ catholique de Louvain Place Cardinal Mercier, 10 1348 Louvain-la-Neuve, Belgium [email protected] Abstract norms (Bestgen, 2002; Kamps et al., 2004; Esuli and Sebastiani, 2006; Bestgen and Vincze, 2012). This paper describes the system developed by The Lexical Complexity Prediction (LCP) the Laboratoire d’analyse statistique des textes shared task at SemEval-2021 requires exactly the (LAST) for the Lexical Complexity Prediction development of such techniques (Shardlow et al., shared task at SemEval-2021. The proposed 2021a). It is indeed a question of estimating the system is made up of a LightGBM model fed with features obtained from many word fre- lexical complexity, the degree of difficulty of the quency lists, published lexical norms and psy- words in a text. This dimension is important in NLP chometric data. For tackling the specificity applications for simplifying texts and assisting spe- of the multi-word task, it uses bigram associ- cific populations such as people with reading dis- ation measures. Despite that the only contex- abilities or who are learning a foreign language. A tual feature used was sentence length, the sys- specificity of the LCP task is that it relates not only tem achieved an honorable performance in the to words but also to multi-word expressions which multi-word task, but poorer in the single word task. The bigram association measures were are very rarely taken into account in norms and in found useful, but to a limited extent. -

Linguistic and Cognitive Features of Figurative Language Processing and Production
Georgia State University ScholarWorks @ Georgia State University Applied Linguistics and English as a Second Department of Applied Linguistics and English Language Dissertations as a Second Language 4-30-2018 Beyond Literal Meaning: Linguistic And Cognitive Features Of Figurative Language Processing And Production STEPHEN SKALICKY Follow this and additional works at: https://scholarworks.gsu.edu/alesl_diss Recommended Citation SKALICKY, STEPHEN, "Beyond Literal Meaning: Linguistic And Cognitive Features Of Figurative Language Processing And Production." Dissertation, Georgia State University, 2018. https://scholarworks.gsu.edu/alesl_diss/44 This Dissertation is brought to you for free and open access by the Department of Applied Linguistics and English as a Second Language at ScholarWorks @ Georgia State University. It has been accepted for inclusion in Applied Linguistics and English as a Second Language Dissertations by an authorized administrator of ScholarWorks @ Georgia State University. For more information, please contact [email protected]. BEYOND LITERAL MEANING: LINGUISTIC AND COGNITIVE FEATURES OF FIGURATIVE LANGUAGE PROCESSING AND PRODUCTION by STEPHEN SKALICKY Under the Direction of Scott Crossley, PhD ABSTRACT Figurative language, such as metaphor and irony, has been studied by researchers in a wide variety of fields for the past several decades. A primary goal of this research has been to determine the processes underlying figurative language comprehension (e.g., how the figurative meaning of a metaphor is processed when compared to its literal meaning). While this research has led to a better understanding of the relation between figurative meaning and surface linguistic form, it has also served to underemphasize other potentially important influences on figurative language use, such as participant individual differences (e.g., cognitive ability, language background), linguistic features (e.g., lexical sophistication), and affective perceptions (e.g., humorous reactions).