3 Innovative Techniques for the Characterization of Morphological
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

38005 38114 Allemond 38008 38970 Ambel 38014 38510 Arandon
Code Code Postal Commune INSEE 38005 38114 Allemond 38008 38970 Ambel 38014 38510 Arandon 38017 38150 Assieu 38019 38550 Auberives-sur-Varèze 38020 38142 Auris 38023 38650 Avignonet 38027 38530 Barraux 38039 38190 Bernin 38041 38160 Bessins 38044 38690 Biol 38053 38300 Bourgoin-Jallieu 38066 38122 Chalons 38070 38190 Champ-Près-Froges 38072 38150 Chanas 38083 38390 Charette 38086 38470 Chasselay 38087 38670 Chasse-sur-Rhône 38095 38160 Chatte (ouverture partielle) 38098 38730 Chelieu 38099 38160 Chevrières 38101 38550 Cheyssieu 38102 38300 Chèzeneuve 38109 38460 Chozeau 38113 38930 Clelles 38116 38350 Cognet 38125 38710 Cordéac 38127 38710 Cornillon-en-Trièves 38128 38970 Corps 38140 38920 Crolles 38145 38160 Dionay 38147 38730 Doissin 38149 38300 Domarin 38154 38740 Entraigues 38175 38190 Froges 38176 38290 Frontonas 38181 38570 Goncelin 38186 38650 Gresse-en-Vercors 38062 38530 La Buissière 38076 38110 La Chapelle-de-la-Tour 38166 38530 La Flachère 38177 38520 La Garde 38264 38350 La Morte 38265 38770 La Motte-d'Aveillans 38266 38770 La Motte-Saint-Martin 38269 38350 La Mure 38303 38570 La Pierre 38469 38970 La Salette-Fallavaux Code Code Postal Commune INSEE 38495 38840 La Sône 38503 38660 La Terrasse 38521 38350 La Valette 38537 38290 La Verpillière 38206 38190 Laval 38207 38350 Lavaldens 38208 38710 Lavars 38052 38520 Le Bourg-d'Oisans 38100 38570 Le Cheylas 38173 38142 Le Freney-d'Oisans 38302 38740 Le Périer 38511 38660 Le Touvet 38002 38190 Les Adrets 38131 38138 Les Côtes-d'Arey 38132 38970 Les Côtes-de-Corps 38193 38080 L'Isle-d'Abeau -

Arrêté Préfectoral N°DREAL-2016
PRÉFET DE L’ISÈRE Direction régionale de l’environnement, de l’aménagement et du logement Auvergne-Rhône-Alpes Unité départementale de l'Isère Pôle Climat Air Énergie (PRICAE) Grenoble, le 26 mai 2016 Arrêté préfectoral n°DREAL-2016 relatif à la mise en œuvre de la mesure 11 du plan de protection de l’atmosphère (PPA) de la région grenobloise : conformité des installations de combustion individuelles utilisant de la biomasse et mises en service dans les communes du périmètre du PPA Le Préfet de l'Isère Chevalier de la Légion d'Honneur Chevalier de l'Ordre National du Mérite Vu le code de l’environnement et notamment ses articles L.222-4 à L.222-7, et R.222-13 à R.222-36 ; Vu l’arrêté inter-préfectoral n°2014056-0035 du 25 février 2014 approuvant le projet de révision du plan de protection de l’atmosphère (PPA) de la région grenobloise ; Vu le décret n°2004-374 modifié du 29 avril 2004, relatif aux pouvoirs des préfets, à l’organisation et à l’action des services de l’État dans les régions et départements et notamment son article 43 ; Vu le plan régional pour la qualité de l’air de la région Rhône-Alpes approuvé par arrêté préfectoral du 1er février 2001 ; Vu le plan de protection de l’atmosphère de la région grenobloise et particulièrement sa mesure n°11 : « Interdire l’installation d’appareils de chauffage au bois non performants sur la zone PPA » ; Vu le rapport de synthèse de la direction régionale de l’environnement, de l’aménagement et du logement Auvergne-Rhône-Alpes, unité départementale de l'Isère (DREAL-UDI), du 2 février 2016 -

À La Découverte
NOUS CONTACTER Randonnée des passerelles 04 76 34 14 48 www.lac-monteynard.com Bateau La Mira 04 76 34 14 56 À la découverte www.la-mira.com Lac Monteynard Bateau La Mira Depuis Treffort (30 minutes de Grenoble) ou Mayres-Savel (15 minutes de La Mure) Point information Parking Prenez le temps… LES ARNAUDS 770m De séjourner Hôtel restaurant Gîte ou Chambre d’hôte L Camping Restauration a c RIVE DROITE d e ROUAC Épicerie Aire de camping car SAVEL | MAYRES-SAVEL | SAINT-AREY M 658m o n Toilettes t Point eau › Camping de Savel e y n Bord du lac, école de voile, location de VTT a Port Location de bateau r d Sert de Chèvrier à assistance électrique, location de bateaux, - 700m Mise à l’eau Ski nautique A paint-ball, massages v i TREFFORT g n Marcieu Club de kitesurf Point de vue 04 76 81 14 79 VILLAGE o n 610m e › Domaine des Genevreys - Saint-Arey t Aire de jeux Aire de pique-nique 04 76 81 26 27 › Maison d'hôtes et Gîte Le Pellenfrey - Saint-Arey La Croix Table d’orientation Curiosité naturelle 605m Patrimoine religieux Curiosité patrimoniale 06 32 88 17 82 Treffort › Gîtes "L'Échappée Belle" TREFFORT le Lac Location de vélos Embarcadère LE LAC 560m électriques La Mira La Motte-Saint-Martin 560m 06 28 77 02 83 Paintball Sous Jullières › Gîtes de Roubanis - La Motte-Saint-Martin 560m Embarcadère 06 33 00 90 47 La Mira › Gîte le Sénépy - Mayres-Savel Orchidées 04 76 40 79 40 527m Les Champs CHATEAU DE SAVEL › Auberge Rurale - Mayres-Savel Parking 550m 04 76 81 09 31 Combettes › Chambres d’Hôtes - Mayres-Savel Ruisseau 04 76 81 09 31 Béranger -

Characterization of the Avignonet Landslide (French Alps) with Seismic Techniques
Landslides and Engineered Slopes – Chen et al. (eds) © 2008 Taylor & Francis Group, London, ISBN 978-0-415-41196-7 Characterization of the Avignonet landslide (French Alps) with seismic techniques D. Jongmans, F. Renalier, U. Kniess, S. Schwartz, E. Pathier & Y. Orengo LGIT, Université Joseph Fourier, Grenoble Cedex 9, France G. Bièvre LGIT, Université Joseph Fourier, Grenoble Cedex 9, France CETE de Lyon, Laboratoire Régional d’Autun, Autun cedex, France T. Villemin LGCA, Université de Savoie, France C. Delacourt Domaines Océaniques, UMR6538, IUEM, Université de Bretagne Occidentale, France ABSTRACT: The large Avignonet landslide (40 106 m3) is located in the Trieves area (French Alps) which is covered by a thick layer of glacio-lacustrine clay.× The slide is moving slowly at a rate varying from 1 cm/year near the upper scarp to over 13 cm/year at the toe. A preliminary geophysical campaign was performed in order to test the sensitivity of geophysical parameters to the gravitational deformation. In the saturated clays where the landslide occurs, the electrical resistivity and P-wave velocity are little affected by the slide. On the contrary, S-wave velocity (Vs) values in the first ten meters were found to be inversely correlated with the measured displacement rates along the slope. These results highlight the interest of measuring Vs values in the field for characterising slides in saturated clays and of developing techniques allowing the 2D and 3D imaging of slides. 1 INTRODUCTION Schmutz et al. 2000, Lapenna et al. 2005, Grandjean et al. 2006, Méric et al. 2007) seismic and electrical Slope movements in clay formations are world methods were successfully used in clay deposits for widespread and usually result from complex defor- distinguishing the mass in motion from the unaffected mation processes, including internal strains in the ground. -

Passerelles Himalayennes Du Monteynard
Passerelles himalayennes du Monteynard Une randonnée proposée par Bisserain73 C'est une balade qui commence par une traversée en bateau. L'objectif est d'emprunter les deux élégantes passerelles. La première passerelle franchit le Drac. La seconde passerelle franchit l'Ebron. Balisage satisfaisant. Randonnée n°73182 Durée : 5h25 Difficulté : Moyenne Distance : 15.3km Retour point de départ : Oui Dénivelé positif : 361m Activité : A pied Dénivelé négatif : 349m Régions : Alpes, Dauphiné Point haut : 696m Commune : Treffort (38650) Point bas : 480m Description (D/A) Se rendre à l'embarcadère de Treffort. La traversée en bateau dure Points de passages de quinze à vingt minutes, elle est assortie des commentaires du pilote. D/A Embarcadère de Treffor - Lac de (1) Après avoir débarqué à Mayres-Savel, partir Sud Est par un chemin qui Monteynard-Avignonet va rejoindre la route D116A. N 44.906835° / E 5.672175° - alt. 481m - km 0 Suivre la route sur quelques centaines de mètres, puis après un virage, 1 Mayres-Savel s'engager dans un sentier qui part à droite (balisage: Passerelle du Drac). N 44.880419° / E 5.688852° - alt. 480m - km 3.47 (2) Peu après, le sentier va se transformer en chemin agréable. La 2 Sentier vers la passerelle passerelle sur le Drac va bientôt apparaître dans le paysage. N 44.87321° / E 5.704184° - alt. 552m - km 5.5 Poursuivre jusqu’à la passerelle. 3 Passerelle sur le - Drac (rivière) - Drac Noir- (3) Emprunter la passerelle ( longueur 220 m). Sur l'autre rive, continuer Drac par le sentier qui part à droite. N 44.869587° / E 5.709323° - alt. -
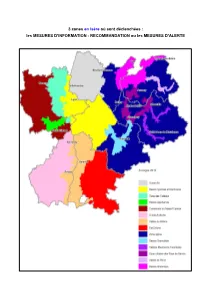
Quelles Communes
3 zones en Isère où sont déclenchées : les MESURES D’INFORMATION - RECOMMANDATION ou les MESURES D’ALERTE 1 1 - Communes iséroises de la zone Nord Isère LES ABRETS COURTENAY PARMILIEU SAINT-MAURICE-L'EXIL AGNIN CRACHIER LE PASSAGE SAINT-MICHEL-DE-SAINT- L'ALBENC CRAS PASSINS GEOIRS ANJOU CREMIEU LE PEAGE-DE- SAINT-ONDRAS ANNOISIN-CHATELANS CREYS-MEPIEU ROUSSILLON SAINT-PAUL-D'IZEAUX ANTHON CULIN PENOL SAINT-PIERRE-DE- AOSTE DIEMOZ LE PIN BRESSIEUX APPRIEU DIONAY PISIEU SAINT-PRIM ARANDON DIZIMIEU PLAN SAINT-QUENTIN- ARTAS DOISSIN POLIENAS FALLAVIER ARZAY DOLOMIEU POMMIER-DE- SAINT-ROMAIN-DE- ASSIEU DOMARIN BEAUREPAIRE JALIONAS AUBERIVES-SUR-VAREZE ECLOSE LE PONT-DE-BEAUVOISIN SAINT-ROMAIN-DE-SURIEU LES AVENIERES LES EPARRES PONT-DE-CHERUY SAINT-SAUVEUR BADINIERES ESTRABLIN PONT-EVEQUE SAINT-SAVIN BALBINS EYDOCHE PORCIEU-AMBLAGNIEU SAINT-SIMEON-DE- LA BALME-LES-GROTTES EYZIN-PINET PRESSINS BRESSIEUX LA BATIE-DIVISIN FARAMANS PRIMARETTE SAINT-SORLIN-DE- LA BATIE-MONTGASCON FAVERGES-DE-LA-TOUR QUINCIEU MORESTEL BEAUFORT FITILIEU REAUMONT SAINT-SORLIN-DE-VIENNE BEAULIEU FLACHERES REVEL-TOURDAN SAINT-SULPICE-DES- BEAUREPAIRE LA FORTERESSE REVENTIN-VAUGRIS RIVOIRES BEAUVOIR-DE-MARC FOUR ROCHE SAINT-VERAND BELLEGARDE-POUSSIEU LA FRETTE LES ROCHES-DE- SAINT-VICTOR-DE- BELMONT FRONTONAS CONDRIEU CESSIEU BESSINS GILLONNAY ROCHETOIRIN SAINT-VICTOR-DE- BEVENAIS LE GRAND-LEMPS ROMAGNIEU MORESTEL BILIEU GRANIEU ROUSSILLON SALAGNON BIOL GRENAY ROYAS SALAISE-SUR-SANNE BIZONNES HEYRIEUX ROYBON SARDIEU BLANDIN HIERES-SUR-AMBY RUY SATOLAS-ET-BONCE BONNEFAMILLE -

A New Technique for the Detection of Large Scale Landslides in Glacio
1 A new technique for the detection of large scale landslides in glacio-lacustrine deposits using 2 image correlation based upon aerial imagery: a case study from the French Alps 3 Paz Fernandez 1 and Malcolm Whitworth 2 4 1 Department of Civil Engineering, ETSICCP, University of Granada, Campus de Fuentenueva, E- 5 18071, Granada, Spain e-mail: [email protected] 6 2 School of Earth and Environmental Sciences, University of Portsmouth, Burnaby Road, Portsmouth 7 PO1 3QL. United Kingdom. Email: [email protected] 8 Abstract 9 Landslide monitoring has benefited from recent advances in the use of image correlation of high 10 resolution optical imagery. However, this approach has typically involved satellite imagery that may 11 not be available for all landslides depending on their time of movement and location. This study has 12 investigated the application of image correlation techniques applied to a sequence of aerial imagery 13 to an active landslide in the French Alps. We apply an indirect landslide monitoring technique (COSI- 14 Corr) based upon the cross-correlation between aerial photographs, to obtain horizontal 15 displacement rates. Results for the2001–2003 time interval are presented, providing a spatial model 16 of landslide activity and motion across the landslide, which is consistent with previous studies. The 17 study has identified areas of new landslide activity in addition to known areas and through image 18 decorrelation has identified and mapped two new lateral landslides within the main landslide 19 complex. This new approach for landslide monitoring is likely to be of wide applicability to other 20 areas characterised by complex ground displacements. -

Pêche En 2019
République Française Département de l'Isère PÉRIODES D'OUVERTURE et de CLÔTURE de la PÊCHE EN 2019 AVIS ANNUEL APPLICATION DES DISPOSITIONS SUIVANTES: Articles L 436-5 et R 436.6 à R 436-65 du Code de l’Environnement, réglementant la pêche en eau douce. Articles L 431-3, L 436-5 – 10ème alinéa, R 436-43 du Code de l’Environnement, déterminant les conditions de classement des cours d’eau, canaux et plans d’eau en deux catégories. Arrêté ministériel du 23 novembre 1990, paru au J.O. du 10/01/91 fixant le classement des cours d’eau, canaux et plans d’eau en deux catégories, en particulier dans le département de l’Isère. Arrêtés ministériels du 5 mai 1986 modifié, du 3 Août 1995 et du 31 Août 2004, fixant la liste des grands lacs intérieurs de montagne pouvant être soumis à une réglementation particulière, dont le lac de Paladru, le lac de Monteynard-Avignonet et les 10 lacs de montagne suivants : Labarre, la Muzelle, lac blanc de Belledonne, lac de Crop, lacs du petit et du grand Domeynon, lac de la Fare, lac de la Folle, lacs blanc ou Layta et lac Noir. Arrêté réglementaire N° 38-2018-12-12-002 du 12 décembre 2018 relatif à l’exercice de la pêche en eau douce dans le département de l’Isère pour l’année 2019. LA PÊCHE EST AUTORISÉE DANS LE DÉPARTEMENT DE L’ISÈRE PENDANT LES PÉRIODES D’OUVERTURE SUIVANTES : COURS D’EAU COURS D’EAU DÉSIGNATION GRANDS LACS INTÉRIEURS ET PLAN D’EAU ET PLANS D’EAU DE 2ème DES ESPÈCES OU DE MONTAGNE DE 1ère CATÉGORIE CATÉGORIE Toutes espèces du 2ème samedi de mars Pour mémoire conformément sauf dérogations -

Département De L'isère
Département de l'Isère Délimitation des zones de sismicité Prévention du risque sismique pour les bâtiments, équipements et installations de la classe dite "à risque normal" Décret n° 2010-1255 du 22 octobre 2010 Vertrieu Parmilieu La Balme Porcieu les-Grottes Amblagnieu Montalieu Charette Hières Vercieu sur-Amby Saint-Baudille Bouvesse Anthon Quirieu Villette-d'Anthon de-la-Tour Chavanoz Vernas Saint-Romain Annoisin Chatelans Pont-de de-Jalionas O Janneyrias ptevoz Creys Chéruy Leyrieu Mépieu Tignieu Siccieu Charvieux S Jameyzieu Crémieu aint-Julien Courtenay Chavagneux et-Carisieu Vill Arandon emoirieu Dizimieu Saint-Victor Soleymieu de-Morestel Chozeau Chamagnieu Moras Passins Brangues Trept M Satolas Veyssilieu Saint-Hilaire orestel et-Bonce Le Bouchage Panossas de Brens Salagnon Sermerieu Vezeronc Vénérieu Grenay -Curtin Les Avenières Frontonas Saint Saint-Marcel Saint-Sorlin Chef Vignieu Veyrins Saint-Quentin Bel-Accueil de-Morestel La Verpillière Thuellin Fallavier Vasselin Heyrieux Vaulx Saint-Savin L'Isle-d'Abeau Dolomieu et-Milieu Corbelin Montcarra Saint-Jean Gra Villefontaine Bourgoin-Jallieu Faverges nieu Valencin de-Soudain de-la-Tour Bonnefamille Sa Ruy Aoste Villette int-Alban Rochetoirin La Chapelle Saint-Just de-Roche de-Vienne Luzinay Diémoz de-la-Tour La Batie Chaleyssin Chimilin Chasse-sur Roche Domarin Nivolas La Tour Saint-Clair Montgascon Cessieu Rhone Chuzelles Four Maubec Vermelle du-Pin de-la-Tour Romagnieu Oytier Saint-Georges Sérezin-de Fitilieu C Meyrié Saint-André Saint-Oblas d'Espéranche hezeneuve la-Tour -

Fiche Horaire Ligne : CLE01 - ST MARTIN DE CLELLES-CLELLES ECOLES
Fiche Horaire Ligne : CLE01 - ST MARTIN DE CLELLES-CLELLES ECOLES Période scolaire : Oui Oui Nota : A Itinéraires CLE0100 CLE0102 Services 1 1 INSEE Commune Code Point d'arrêt lmmjv--- lmmjv--- 38419 00 SAINT MARTIN DE CLELLES 10306 VILLAGE 07:35 08:36 10290 LA CHABANNERIE 07:40 08:41 10309 LES TRAVERSES 07:42 08:43 10149 LES RIPPERTS 07:45 08:46 38113 00 CLELLES 20309 GROUPE SCOLAIRE 08:55 10133 MAIRIE 07:49 Transporteur AUTOCARS ET VOYAGES VILLE JEAN LOUIS Nota A - Correspondance à Clelles avec la ligne MEN05. Fiche Horaire Ligne : CLE01 - ST MARTIN DE CLELLES-CLELLES ECOLES Période scolaire : Oui Oui Oui Nota : A A Itinéraires CLE0105 CLE0103 CLE0105 Services 2 1 1 INSEE Commune Code Point d'arrêt --m----- --m----- lm-jv--- 38113 00 CLELLES 20310 GROUPE SCOLAIRE 12:05 17:10 10132 MAIRIE 12:07 13:37 17:12 10137 LOT THEYSSONNIERE 12:09 13:39 17:14 10142 GENDARMERIE 12:13 13:43 17:18 38419 00 SAINT MARTIN DE CLELLES 10306 VILLAGE 12:17 13:47 17:22 10290 LA CHABANNERIE 12:23 13:51 17:28 10309 LES TRAVERSES 12:27 13:55 17:32 10148 LES RIPPERTS 12:33 14:00 17:38 Transporteur AUTOCARS ET VOYAGES VILLE JEAN LOUIS Nota A - Correspondance à Clelles avec la ligne MEN05. Fiche Horaire Ligne : MEN01 - ST JEAN D'HERANS-MENS Période scolaire : Oui Oui Itinéraires MEN0100 MEN0102 Services 1 1 INSEE Commune Code Point d'arrêt lmmjv--- lmmjv--- 38403 00 SAINT JEAN D'HERANS 10346 CITE E.D.F. 07:50 08:03 10345 LES RIVES 07:53 08:05 10365 ECOLE PRIMAIRE 08:15 10341 LA JARGNE 07:55 10359 LE VILLAGE 08:00 10354 TOUAGE-PONT.RD34B 08:05 10350 VILLARD TOUAGE -

Département De L'isère
Département de l'Isère Délimitation des zones de sismicité Prévention du risque sismique pour les bâtiments, équipements et installations de la classe dite "à risque normal" Décret n° 2010-1255 du 22 octobre 2010 Vertrieu Parmilieu La Balme Porcieu les-Grottes Amblagnieu Montalieu Charette Hières Vercieu sur-Amby Saint-Baudille Bouvesse Anthon Quirieu Villette-d'Anthon de-la-Tour Chavanoz Vernas Saint-Romain Annoisin Chatelans Pont-de de-Jalionas O Janneyrias ptevoz Creys Chéruy Leyrieu Mépieu Tignieu Siccieu Charvieux S Jameyzieu Crémieu aint-Julien Courtenay Chavagneux et-Carisieu Vill Arandon emoirieu Dizimieu Saint-Victor Soleymieu de-Morestel Chozeau Chamagnieu Moras Passins Brangues Trept M Satolas Veyssilieu Saint-Hilaire orestel et-Bonce Le Bouchage Panossas de Brens Salagnon Sermerieu Vezeronc Vénérieu Grenay -Curtin Les Avenières Frontonas Saint Saint-Marcel Saint-Sorlin Chef Vignieu Veyrins Saint-Quentin Bel-Accueil de-Morestel La Verpillière Thuellin Fallavier Vasselin Heyrieux Vaulx Saint-Savin L'Isle-d'Abeau Dolomieu et-Milieu Corbelin Montcarra Saint-Jean Gra Villefontaine Bourgoin-Jallieu Faverges nieu Valencin de-Soudain de-la-Tour Bonnefamille Sa Ruy Aoste Villette int-Alban Rochetoirin La Chapelle Saint-Just de-Roche de-Vienne Luzinay Diémoz de-la-Tour La Batie Chaleyssin Chimilin Chasse-sur Roche Domarin Nivolas La Tour Saint-Clair Montgascon Cessieu Rhone Chuzelles Four Maubec Vermelle du-Pin de-la-Tour Romagnieu Oytier Saint-Georges Sérezin-de Fitilieu C Meyrié Saint-André Saint-Oblas d'Espéranche hezeneuve la-Tour -

Zone Alpine Isère Activation De La Procédure Préfectorale D’Alerte De Niveau N1
INFORMATION PREFECTORALE Épisode de pollution de l'air de type mixte (PM !" sur le #assin $one alpine Isère A&ti'ation de la proc(dure pr()e&torale d*alerte de ni'eau N Grenoble, le mercredi 24 février 2021 Compte tenu des prévisions émises par Atmo Auvergne Rhône Alpes, la pro&(dure pr()e&torale d*alerte de ni'eau N est activée ! compter d’au#ourd’hui pour le bassin d’air zone alpine %s&re' (es mesures détaillées ci dessous, qui visent ! réduire les sources d’émissions polluantes, prennent effet ! compter de ce #our ! 1*h00 ! l"e+ception des mesures relatives au secteur du transport qui sont mises en ,uvre à partir du #eudi 25 février 2021 à 05h00' Mesures relati'es au se&teur du transport • .n abaissement temporaire de la vitesse de 20 /m0h est instauré, pour tous les véhicules ! moteur, sur tous les a+es routiers du bassin d’air $one alpine %s&re o1 la vitesse maximale autorisée est habituellement supérieure ou égale ! 20 /m0h' (es a+es sur lesquels la vitesse autorisée est égale ! 80 km0h sont limités à *0 /m0h' • .ne modification du format des compétitions mécaniques ! moteur thermique est instaurée en réduisant les temps d’entra4nement et d’essai dans la zone alpine %s&re. Mesures relati'es au se&teur r(sidentiel • ("utilisation du bois et de ses dérivés comme chauffage individuel d’appoint ou d’agrément est interdit' • (a pratique du br5lage des déchets est totalement interdite 6 les éventuelles dérogations sont suspendues' • (a température de chauffage des b7timents doit 8tre ma4trisée et réduite, en mo9enne volumique, ! 13 :C'