Quickly Finding a Benign Region Via Heavy Ball Momentum in Non
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Loud Proud Passion and Politics in the English Defence League Makes Us Confront the Complexities of Anti-Islamist/Anti-Muslim Fervor
New Ethnographies ‘These voices of English nationalism make for difficult listening. The great strength of Hilary PILKINGTON Pilkington’s unflinching ethnography is her capacity to confound and challenge our political and preconceptions and makes us think harder. This is an important, difficult and brave book.’ Les Back, Professor of Sociology, Goldsmiths, University of London ‘Pilkington offers fresh and crucial insights into the politics of fear. Her unflinchingly honest depiction of the EDL breaks apart stereotypes of rightist activists as simply dupes, thugs, and racists and Loud proud PASSION AND POLITICS IN THE ENGLISH DEFENCE LEAGUE makes us confront the complexities of anti-Islamist/anti-Muslim fervor. This terrific, compelling book is a must-read for scholars and readers concerned about the global rise of populist movements on the right.’ Kathleen Blee, Distinguished Professor of Sociology, University of Pittsburgh Loud and proud uses interviews, informal conversations and extended observation at English Defence League events to critically reflect on the gap between the movement’s public image and activists’ own understandings of it. It details how activists construct the EDL and themselves as ‘not racist, not violent, just no longer silent’ through, among other things, the exclusion of Muslims as a possible object of racism on the grounds that they are a religiously not racially defined Loud group. In contrast, activists perceive themselves to be ‘second-class citizens’, disadvantaged and discriminated against by a two-tier justice system that privileges the rights of others. This failure to recognise themselves as a privileged white majority explains why ostensibly intimidating EDL street demonstrations marked by racist chanting and nationalistic flag waving are understood by activists as standing ‘loud and proud’; the only way of being heard in a political system governed by a politics of silencing. -
Modern Physics, the Nature of the Interaction Between Particles Is Carried a Step Further
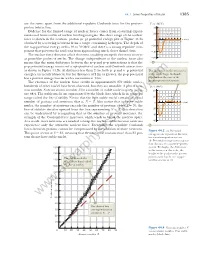
44.1 Some Properties of Nuclei 1385 are the same, apart from the additional repulsive Coulomb force for the proton– U(r ) (MeV) proton interaction. 40 Evidence for the limited range of nuclear forces comes from scattering experi- n–p system ments and from studies of nuclear binding energies. The short range of the nuclear 20 force is shown in the neutron–proton (n–p) potential energy plot of Figure 44.3a 0 r (fm) obtained by scattering neutrons from a target containing hydrogen. The depth of 1 567432 8 the n–p potential energy well is 40 to 50 MeV, and there is a strong repulsive com- Ϫ20 ponent that prevents the nucleons from approaching much closer than 0.4 fm. Ϫ40 The nuclear force does not affect electrons, enabling energetic electrons to serve as point-like probes of nuclei. The charge independence of the nuclear force also Ϫ60 means that the main difference between the n–p and p–p interactions is that the a p–p potential energy consists of a superposition of nuclear and Coulomb interactions as shown in Figure 44.3b. At distances less than 2 fm, both p–p and n–p potential The difference in the two curves energies are nearly identical, but for distances of 2 fm or greater, the p–p potential is due to the large Coulomb has a positive energy barrier with a maximum at 4 fm. repulsion in the case of the proton–proton interaction. The existence of the nuclear force results in approximately 270 stable nuclei; hundreds of other nuclei have been observed, but they are unstable. -

Bill Gibson and Mark Setterfield Real and Financial Crises in the Keynes
Bill Gibson and Mark Setterfield Real and financial crises in the Keynes-Kalecki structuralist model: An agent-based approach August 2015 Working Paper 17/2015 Department of Economics The New School for Social Research The views expressed herein are those of the author(s) and do not necessarily reflect the views of the New School for Social Research. © 2015 by Bill Gibson and Mark Setterfield. All rights reserved. Short sections of text may be quoted without explicit permission provided that full credit is given to the source. Real and financial crises in the Keynes-Kalecki structuralist model: An agent-based approach Bill Gibsonyand Mark Setterfieldyy1 Abstract Agent-based models are inherently microstructures{with their attention to agent behavior in a field context{and only aggregate up to systems with recognizable macroeconomic char- acteristics. One might ask why the traditional Keynes-Kalecki or structuralist (KKS) model would bear any relationship to the multi-agent modeling approach. This paper shows how KKS models might benefit from agent-based microfoundations, without sacrificing tradi- tional macroeconomic themes, such as aggregate demand, animal sprits and endogenous money. Above all, the integration of the two approaches gives rise to the possibility that a KKS system{stable over many consecutive time periods{might lurch into an uncontrollable downturn, from which a recovery would require outside intervention. As a by-product of the integration of these two popular approaches, there emerges a cogent analysis of the network structure necessary to bind real and financial agents into a integrated whole. It is seen, contrary to much of the existing literature, that a highly connected financial system does not necessarily lead to more crashes of the integrated system. -

Immune Responses to AAV in Clinical Trials
Current Gene Therapy, 2011, 11, 321-330 321 Immune Responses to AAV in Clinical Trials Federico Mingozzi1 and Katherine A. High1,2,* 1Children’s Hospital of Philadelphia, Philadelphia, PA, USA; 2Howard Hughes Medical Institute, Philadelphia, PA, USA Abstract: Findings in the first clinical trial in which an adeno-associated virus (AAV) vector was introduced into the liver of human subjects highlighted an issue not previously identified in animal studies. Upon AAV gene transfer to liver, two subjects developed transient elevation of liver enzymes, likely as a consequence of immune rejection of transduced hepa- tocytes mediated by AAV capsid-specific CD8+ T cells. Studies in healthy donors showed that humans carry a population of antigen-specific memory CD8+ T cells probably arising from wild-type AAV infections. The hypothesis formulated at that time was that these cells expanded upon re-exposure to capsid, i.e. upon AAV-2 hepatic gene transfer, and cleared AAV epitope-bearing transduced hepatocytes. Other hypotheses have been formulated which include specific receptor- binding properties of AAV-2 capsid, presence of capsid-expressing DNA in AAV vector preparations, and expression of alternate open reading frames from the transgene; emerging data from clinical trials however fail to support these compet- ing hypotheses. Possible solutions to the problem are discussed, including the administration of a short-term immunosup- pression regimen concomitant with gene transfer, or the development of more efficient vectors that can be administered at lower doses. While more studies will be necessary to define mechanisms and risks associated with capsid-specific im- mune responses in humans, monitoring of these responses in clinical trials will be essential to achieving the goal of long- term therapeutic gene transfer in humans. -

The Art Issue
C & 0 Canal Association concerned with the conservation of the natural and historical environment of the C&O Canal and the Potomac River Basin VOLUME XXVIII SEPTEMBER 1996 NUMBER3 THE ART ISSUE JACK DURHAM AND HIS PAINTINGS On May 25, the C&O Canal silent auction opened at the D&D Art Gallery at 1618 Wisconsin Avenue NW in Georgetown. Exhibited were 22 paintings by Jack Durham. In addition, there were canal-related paintings or photographs by Elizabeth Miles Cooke, Dara Friel, Delilah Hawa, Peter Hill, Andrei Kushner, Debbie Niichell LeBlanc, Gustavo Mogollon, Suzanne Twyforde ·and Ethel Durham. The works by Jack Durham, around which this exhibition was built, were donated by his daughter, Nancy Durham Robinson, of Richmond, Vermont. Mrs. Robinson wanted the sales proceeds donated to help repair the January flood damage. The silent auction, which continued on the following day, March 26, was also held on the weekends, of June 1-2, June 8-9, June 15-16, and June 22-23 from 2-4 p.m . ----------~- -~~--~~-~--~--~---· -'~-- -~-~--~-~-:!""". ,_ __ _ •....... ' Jack Durham - a portrait courtesy of Delilah Hawa - ulwlf I Jack Durham helped to found the C&O Canal Association- and took the lead in organizing and managing the original Douglas f hike in March 1954. He left to the Association his archives, I which include not only important documents and photographs pertaining to the hike, the dramatic event that saved the canal I from being paved over for a highway, but also to the Association's establishment and early history. Durham spent his career as a public relations official for several government agencies in Washington. -

Albuquerque Morning Journal, 12-08-1911 Journal Publishing Company
University of New Mexico UNM Digital Repository Albuquerque Morning Journal 1908-1921 New Mexico Historical Newspapers 12-8-1911 Albuquerque Morning Journal, 12-08-1911 Journal Publishing Company Follow this and additional works at: https://digitalrepository.unm.edu/abq_mj_news Recommended Citation Journal Publishing Company. "Albuquerque Morning Journal, 12-08-1911." (1911). https://digitalrepository.unm.edu/ abq_mj_news/2229 This Newspaper is brought to you for free and open access by the New Mexico Historical Newspapers at UNM Digital Repository. It has been accepted for inclusion in Albuquerque Morning Journal 1908-1921 by an authorized administrator of UNM Digital Repository. For more information, please contact [email protected]. ALBUQUERQUE MORNING JOURNAL. MEXICO, FRIDAY. DECEMBER 8, 1911. Bj MU 14 Cent ft Month; Single Copte S Cent THIRTY-THIR- D YEAR. VOL CXXXII, No. 69. ALBUQUERQUE, NEW B Carrie, 60 Ornt ft Month. tts condemnation ,f i,..u,e on GUILTY BROTHERS hesruiK c the Los Angeles .UsiiM IT." vggyg it is cloinitsi. the "The universal comU-ninaiio- nf a murderous deed in oir, les ought to be n fact so fsr bevomt question, ' RRE CONDEMNED the statement proceeds, "no e.'.?i'v usvertainable from accessible record, rain TO BUY that no man ith anv regard for his ENTER UNION TRIED reputation lor veracity, could .l.nv it. BY AMERICAN Violence, brutality, destruction of life and property, are foreign m the aims and methods of organ tied labor of America unj no Interest is nn.rc DETECTIVES severely' injured by the empl.nnunt PROSPEROUS FEDERATION of nu h methods than that of the weaker orvanited In the labor move- ment. -

Zuba Central Heat Pump
Zuba Central Heat Pump FOR INSTALLER INSTALLATION MANUAL For safe and correct use, read this manual thoroughly before installing the heat pump unit. English THINK GREEN RG79D356H02_0cover 1 07.8.31, 16:24 Contents: OUTDOOR UNIT Safety Precautions...................................................................................................... 03 Installation Location .................................................................................................. 04 Installing the outdoor unit...........................................................................................06 Installing the refrigerant piping ..................................................................................07 Drainage pipe work.................................................................................................... 09 Electrical work........................................................................................................... 09 Special functions......................................................................................................... 11 -low noise modes -collecting the refrigerant (pump down) AIR HANDLING UNIT Tools and Parts.............................................................................................................13 Installation Requirements............................................................................................ 13 Outdoor system requirements ..................................................................................... 13 Location requirements ............................................................................................... -

Score Alfred Music Publishing Co. Finn
Title: 25th Annual Putnam County Spelling Bee, The - score Author: Finn, William Publisher: Alfred Music Publishing Co. 2006 Description: Score for the musical. Title: 42nd Street - vocal selections Author: Warren, Harry Dubin, Al Publisher: Warner Bros. Publications 1980 Description: Vocal selections from the musical. Contains: About a Quarter to Nine Dames Forty-Second Street Getting Out Of Town Go Into Your Dance The Gold Digger's Song (We're In The Money) I Know Now Lullaby of Broadway Shadow Waltz Shuffle Off To Buffalo There's a Sunny Side to Every Situation Young and Healthy You're Getting To Be a Habit With Me Title: 9 to 5 - vocal selections The musical Author: Parton, Dolly Publisher: Hal Leonard Publishing Corporation Description: Vocal selections from the musical. Contains: Nine to Five Around Here Here for You I Just Might Backwoods Barbie Heart to Hart Shine Like the Sun One of the Boys 5 to 9 Change It Let Love Grow Get Out and Stay Out Title: Addams Family - vocal selections, The Author: Lippa, Andrew Publisher: Hal Leonard Publishing Corporation 2010 Description: Vocal selections from the musical. includes: When You're an Addams Pulled One Normal Night Morticia What If Waiting Just Around the Corner The Moon and Me Happy / Sad Crazier than You Let's Not Talk About Anything Else but Love In the Arms Live Before We Die The Addams Family Theme Title: Ain't Misbehavin' - vocal selections Author: Henderson, Luther Publisher: Hal Leonard Publishing Corporation Description: Vocal selections from the musical. Contains: Ain't Misbehavin (What Did I Do to Be So) Black and Blue (Get Some) Cash For Your Trash Handful of Keys Honeysuckle Rose How Ya Baby I Can't Give You Anything But Love It's a Sin To Tell A Lie I've Got A Felling I'm Falling The Jitterbug Waltz The Joint is Jumping Keepin' Out of Mischief Now The Ladies Who Sing With the Band Looking' Good But Feelin' Bad Lounging at the Waldorf Mean to Me Off-Time Squeeze Me 'Tain't Nobody's Biz-ness If I Do Title: Aladdin and Out - opera A comic opera in three acts Author: Edmonds, Fred Hewitt, Thomas J. -

3 Britney Spears PVG(RHM)
3 Britney Spears PVG(RHM) 72982 5 Jonas Brothers PVG(RHM) 72989 17 Kings Of Leon PVG(RHM) 72411 22 Lily Allen PVG 45616 22 Taylor Swift PVG(RHM) 93924 101 Alicia Keys PVG(RHM) 96442 1001 Yanni PVG(RHM) 75509 1492 Counting Crows PVG(RHM) 67842 1961 The Fray PVG(RHM) 88479 1994 Jason Aldean PVG(RHM) 97854 05-Jun Jason Mraz PVG(RHM) 92135 ...Baby One More Time Britney Spears PV 110926 'O Mare E Tu Andrea Bocelli PVG 103448 'O Sole Mio Giovanni Capurro PV 84897 'O Sole Mio Giovanni Capurro PVG(RHM) 87932 'Round Midnight Thelonious Monk PVG(RHM) 92079 'S Wonderful George Gershwin PVG(RHM) 44924 'Tain't What You Do (It's The WayElla FitzgeraldThat Cha Do It) PVG(RHM) 74394 'Til I Hear You Sing Andrew Lloyd Webber PVG(RHM) 101457 'Til Summer Comes Around Keith Urban PVG(RHM) 70925 'Til Summer Comes Around Keith Urban PVG(RHM) 74111 'Til The Sun Goes Down Boyzone PVG(RHM) 102964 'Til Tomorrow (from Fiorello!) Jerry Bock PVG(RHM) 104346 (All I Can Do Is) Dream You Roy Orbison PVG(RHM) 99501 (Everything I Do) I Do It For YouBryan Adams PVGRHM 152272 (Everything I Do) I Do It For YouBryan (from Adams Robin Hood Prince OfPV Thieves) 46249 (Getting Some) Fun Out Of LifeMadeleine Peyroux PVG(RHM) 47413 (Ghost) Riders In The Sky (A CowboyJohnny Cash Legend) PVG(RHM) 86118 (I Heard That) Lonesome WhistleJohnny Cash PVG(RHM) 86103 (I Wish I Was In) Dixie Daniel Decatur Emmett PVG(RHM) 87928 (I'm A) Road Runner Junior Walker & The All StarsPVG(RHM) 77178 (I'm Going Back To) Himazas Fred Austin PVGRHM 101119 (I've Had) The Time Of My LifeGlee Cast PVG(RHM) -

Renewable Energy Development Professionals V.A.T. 800778381
Renewable Energy Development Professionals V.A.T. 800778381 Curriculum Vitae Education: Studied in the UK (1971-80), graduating from the University of Leeds (1974 – 1980) • B.Sc. Chemical Engineering on Local Education Authority grant • M.Sc. in Fuel and Energy on Science Research Council grant • Ph.D. in Solar Energy on Science Research Council grant (awarded in 1988) Vision and personal statement: I began this wonderful self rewarding journey into the world of renewables in 1978, at Leeds University, with a Ph.D. on Solar Energy. I was lucky to be involved all my professional life with renewables, for 41 years by now, from a junior engineer at P.P.C. in the early 80’s, when I was involved with the installation of Wind and Solar energy projects on the Greek islands, to more recent years as Chairman for consecutive periods of the Wind Energy Association of Greece, CEO of Public Power Corporation’s Renewables subsidiary, as well as head of the Cabinet Office of the deputy Minister for the Environment, Energy and Climate Change Prof. Maniatis. I have also had the privilege to participate in the historic COP21, as well as COP22, COP23 and COP24 global Climate Conferences, while currently I am active in the renewable energy sector in Sub Saharan Africa, based in Kenya. I believe climate change to be the number one threat to our civilisation; hence all our efforts and necessary funds, via a Talanoa inclusive process, guided by the principle of just transition, should be directed towards the more ambitious climate actions needed to meet successfully this unique challenge, as at the moment, we seem to be doing “too little, too late”. -
![Arxiv:1605.08916V1 [Nucl-Th] 28 May 2016 Fietfigsprev Ulia Ela Hi Xie Tts[11 States Excited Emitted Their of As Detection Well As Reactions](https://docslib.b-cdn.net/cover/0616/arxiv-1605-08916v1-nucl-th-28-may-2016-fietfigsprev-ulia-ela-hi-xie-tts-11-states-excited-emitted-their-of-as-detection-well-as-reactions-3850616.webp)
Arxiv:1605.08916V1 [Nucl-Th] 28 May 2016 Fietfigsprev Ulia Ela Hi Xie Tts[11 States Excited Emitted Their of As Detection Well As Reactions
Alpha decay as a probe for the structure of neutron-deficient nuclei Chong Qi Department of Physics, Royal Institute of Technology (KTH), SE-10691 Stockholm, Sweden Abstract The advent of radioactive ion beam facilities and new detector technologies have opened up new possibilities to investigate the radioactive decays of highly unstable nuclei, in particular the proton emission, α decay and heavy cluster decays from neutron-deficient (or proton-rich) nuclei around the proton drip line. It turns out that these decay measurements can serve as a unique probe for studying the structure of the nuclei involved. On the theoretical side, the development in nuclear many-body theories and supercomputing facilities have also made it possible to simulate the nuclear clusterization and decays from a microscopic and consistent perspective. In this article we would like to review the current status of these structure and decay studies in heavy nuclei, regarding both experimental and theoretical opportunities. We then discuss in detail the recent progress in our understanding of the nuclear α formation probabilities in heavy nuclei and their indication on the underlying nuclear structure. 1. Introduction There has been a long history of studies on the α radioactivity which was first described by Ernest + Rutherford in 1899. The structure of the particle was identified by 1907 as 4He (He2 ion) with two protons and two neutrons, which, with the binding energy 7.1 MeV per nucleon, is the most stable configuration below 12C. The greatest challenge then was to understand how the α particle could leave the less stable mother nucleus without any external disturbance. -

Tapping Away Chantilly Toddler Westfield Summer Stage to Present Fights Against Nd Neuroblastoma
Chantilly ❖ Fair Oaks ❖ Fair Lakes ❖ Oak Hill NORTHERN EDITION JULY 15-21, 2010 “Spurred into Action” 25 CENTS Newsstand Price Volume XXIV, NO. 28 Remaining Hopeful for Rachel Tapping Away Chantilly toddler Westfield Summer Stage to present fights against nd neuroblastoma. Broadway musical “42 Street.” By Bonnie Hobbs rable music; you go out of the the- By Bonnie Hobbs Centre View ater humming the tunes.” Centre View Joan Brady Photography Set in the 1930s, the story’s eaturing a cast and crew of about an aspiring chorus girl who olding their more than 100, a 15-piece gets her big break when she fills breath and hop- F orchestra and dazzling cho- in for an injured star in a Broad- H ing for the best, reography by Yvonne Henry, way musical. The 1933 movie gave Chantilly’s Westfield Summer Stage presents hope to Americans suffering Rebecca and Jon D’Andrea con- the musical, “42nd Street.” through the Great Depression. tinually worry what each new It taps its way into the Westfield Then the 1980 Broadway show day will bring their 2-and-a- High theater, Thursday-Sunday, won Tony Awards for Best Musi- half-year-old daughter, Rachel. July 22-25, at 7:30 p.m., with a cal and Best Choreography and They want her cancer to get A few moments of happiness: In a July 2 outing away July 24 matinee at 2 p.m. Tickets ran for nine years, followed by a into remission so she can live from the hospital, Rachel D’Andrea laughs with glee, are $10 in advance at critically acclaimed revival in at home, instead of spending embraced by the love of her parents, Jon and Rebecca.