Optimal Drafting in Hockey Pools
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

General Assembly of North Carolina Session 2005 Ratified Bill
GENERAL ASSEMBLY OF NORTH CAROLINA SESSION 2005 RATIFIED BILL RESOLUTION 2006-13 HOUSE JOINT RESOLUTION 2891 A JOINT RESOLUTION HONORING THE 2006 STANLEY CUP CHAMPION CAROLINA HURRICANES HOCKEY CLUB. Whereas, the Stanley Cup, the oldest trophy competed for by professional athletes in North America, was donated by Frederick Arthur, Lord Stanley of Preston and Governor General of Canada, in 1893; and Whereas, Lord Stanley purchased the trophy for presentation to the amateur hockey champions of Canada; and Whereas, since 1910, when the National Hockey Association took possession of the Stanley Cup, the trophy has been the symbol of professional hockey supremacy; and Whereas, in the year 1971, the World Hockey Association awarded a franchise to the New England Whalers; and Whereas, in 1979, the Whalers played their first regular-season National Hockey League game; and Whereas, in May 1997, Peter Karmanos, Jr., announced that the team would relocate to Raleigh, North Carolina, and be renamed the Carolina Hurricanes; and Whereas, on September 13, 1997, the Carolina Hurricanes played its first preseason game in North Carolina at the Greensboro Coliseum against the New York Islanders; and Whereas, on October 29, 1999, the Carolina Hurricanes played its first game in the Raleigh Entertainment and Sports Arena, now known as the RBC Center; and Whereas, on May 28, 2002, the Carolina Hurricanes won the Eastern Conference Championship, winning its first trip to the Stanley Cup Finals; and Whereas, on June 19, 2006, after playing 107 games and an impressive -
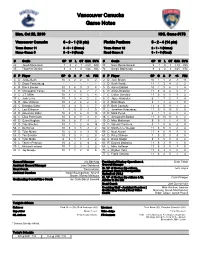
Vancouver Canucks Game Notes
Vancouver Canucks Game Notes Mon, Oct 28, 2019 NHL Game #178 Vancouver Canucks 6 - 3 - 1 (13 pts) Florida Panthers 5 - 2 - 4 (14 pts) Team Game: 11 3 - 0 - 1 (Home) Team Game: 12 2 - 1 - 1 (Home) Home Game: 5 3 - 3 - 0 (Road) Road Game: 8 3 - 1 - 3 (Road) # Goalie GP W L OT GAA SV% # Goalie GP W L OT GAA SV% 25 Jacob Markstrom 7 4 2 1 2.53 .920 33 Sam Montembeault 3 1 0 1 1.79 .933 35 Thatcher Demko 3 2 1 0 1.64 .943 72 Sergei Bobrovsky 9 4 2 3 3.65 .874 # P Player GP G A P +/- PIM # P Player GP G A P +/- PIM 4 D Jordie Benn 10 0 2 2 4 2 2 D Josh Brown 10 1 1 2 -1 11 5 D Oscar Fantenberg - - - - - - 3 D Keith Yandle 11 1 3 4 2 2 6 R Brock Boeser 10 3 6 9 3 4 5 D Aaron Ekblad 10 1 5 6 1 4 8 D Christopher Tanev 10 1 3 4 2 2 6 D Anton Stralman 11 0 4 4 3 2 9 C J.T. Miller 10 4 7 11 5 8 7 C Colton Sceviour 11 0 3 3 -1 2 17 L Josh Leivo 10 1 3 4 2 2 8 C Jayce Hawryluk 6 1 1 2 -1 4 18 R Jake Virtanen 10 2 2 4 2 4 9 C Brian Boyle 3 1 1 2 1 0 20 C Brandon Sutter 10 2 3 5 1 7 10 R Brett Connolly 11 4 5 9 1 4 21 L Loui Eriksson 1 0 0 0 -1 0 11 L Jonathan Huberdeau 11 5 8 13 0 8 23 D Alexander Edler 10 3 3 6 0 10 13 D Mark Pysyk 6 1 1 2 1 2 40 C Elias Pettersson 10 3 8 11 3 0 16 C Aleksander Barkov 11 0 13 13 0 2 43 D Quinn Hughes 10 1 6 7 -1 2 19 D Mike Matheson 9 0 1 1 -1 0 51 D Troy Stecher 10 1 1 2 4 16 21 C Vincent Trocheck 8 1 5 6 -2 0 53 C Bo Horvat 10 5 3 8 -1 2 52 D MacKenzie Weegar 11 3 5 8 2 4 57 D Tyler Myers 10 0 3 3 -1 10 55 C Noel Acciari 11 4 0 4 -1 0 59 C Tim Schaller 10 3 0 3 2 8 61 D Riley Stillman 1 0 0 0 -3 5 64 C Tyler Motte 6 0 1 1 -1 2 62 C Denis Malgin 9 3 5 8 4 2 70 L Tanner Pearson 10 2 2 4 -4 4 63 R Evgenii Dadonov 11 6 3 9 1 0 79 L Micheal Ferland 10 1 2 3 -2 2 68 L Mike Hoffman 11 5 3 8 -1 6 83 C Jay Beagle 10 1 1 2 0 6 73 L Dryden Hunt 11 0 3 3 2 8 77 C Frank Vatrano 11 3 2 5 1 4 General Manager Jim Benning President of Hockey Operations & Dale Tallon Assistant General Manager John Weisbrod General Manager Head Coach Travis Green Sr. -

Buffalo Sabres Digital Press
Buffalo Sabres Daily Press Clips February 9, 2019 Casey Nelson takes a hit and keeps on going in Amerks' conditioning assignment By Bill Hoppe The Buffalo News February 9, 2019 ROCHESTER – Casey Nelson couldn’t even finish one shift Friday. Just 39 seconds into the defenseman’s American Hockey League conditioning assignment, Springfield’s Dryden Hunt checked him from behind, knocking his throat into the dasher board. “Not how you want to start off,” Nelson said after the Americans throttled the Thunderbirds 7-1 in Blue Cross Arena. “It woke me up a little bit.” After spending a few minutes in the dressing room, Nelson, 26, returned and kept taking his regular shift beside Brendan Guhle. Nelson hadn’t played since suffering an upper-body injury with the Sabres on Dec. 4. Waiting 66 days for some game action – “Very antsy,” he acknowledged – was difficult. “I’ve been out for two months,” Nelson said. “It feels like years.” Nelson said his first couple of shifts “felt a little weird.” “But it’s definitely coming back pretty quick,” said Nelson, who has compiled one goal and five points in 22 outings with the Sabres this season. Nelson said his conditioning stint will likely be reevaluated after a few games. The Amerks play a road game against the Utica Comets on Saturday. “He played very well for his first game,” Amerks coach Chris Taylor said. Of course, having played 98 games with the Amerks over the past two seasons, the 6-foot-2, 185-pound Nelson knows the AHL well. “Very physical, a lot of speed,” he said. -

APRAC18-011 Request to Rename Olympus Park
To: Members of the Arenas Parks and Recreation Advisory Committee From: Rob Anderson, Recreation Division Coordinator Meeting Date: April 17, 2018 Subject: Report APRAC18-011 Request to Rename Olympus Park Purpose A report to provide an update on the request to change the name of Olympus Park to Stillman Park. Recommendations That the Arenas Parks and Recreation Advisory Committee approve the recommendations outlined in Report APRAC18-011 dated April 17, 2018, of the Recreation Division Coordinator, as follows: a) That the request to rename Olympus Park as Stillman Park be endorsed; and, b) That Staff be directed to present a report to Council recommending that Olympus Park be renamed Stillman Park. Budget and Financial Implications The approximate $600.00 expense associated with changing the park sign can be accommodated within the approved Park Bench and Sign capital budget (reference number 6-1.03). Report APRAC18-011 – Request to Rename Olympus Park Page 2 Background The Request On March 21, 2017, Mr. Steve Terry submitted a letter to City Hall requesting that consideration be given to renaming Olympus Park as “Stillman Park”, in honour of former National League Hockey Player, Cory Stillman. Olympus Park is a neighbourhood park located in the City’s Northcrest Ward, bordered by Royal Drive and Olympus Avenue. An aerial map showing the park’s location is attached as Appendix “A”. Mr. Terry informed City Staff that he contacted the Stillman family prior to approaching the City, to obtain their support and permission to proceed with the proposed name change. Rationale for the Name Change On April 25, 2017 Mr. -

Victor Hedman (1-1—2) Scored at 14:10 of Double Overtime to Lift the Lightning to the Conference Finals for the Sixth Time In
NHL MORNING SKATE: STANLEY CUP PLAYOFFS EDITION – SEPTEMBER 1, 2020 THREE HARD LAPS * Victor Hedman scored the game-winning goal in double overtime to lift the Lightning to a 4-1 series win over the Bruins and into the Conference Finals for the fourth time in six seasons. * The Avalanche scored five goals in one period of a playoff game for the first time in franchise history and never relinquished the lead to stave off elimination in Game 5. * The Islanders and Golden Knights can both advance to the Conference Finals with a win today. HEDMAN SCORES IN 2OT TO LIFT LIGHTNING TO CONFERENCE FINALS Victor Hedman (1-1—2) scored at 14:10 of double overtime to lift the Lightning to the Conference Finals for the sixth time in franchise history and fourth in the last six seasons. Tampa Bay will now travel to Edmonton for the Eastern Conference Final where they will face the winner of the Flyers-Islanders series. * Hedman became the third Lightning player to score an overtime goal in a series-clinching game, joining Brayden Point earlier this postseason (Game 5 of 2020 R1) and Martin St. Louis (Game 5 of 2004 CQF and 3OT in Game 6 of the 2003 CQF). * Hedman, who became the third Lightning defenseman to score a playoff overtime goal, is just the third blueliner on any team in the last 10 years to score a series-clinching goal in a game that required multiple overtime periods. The others: Kevin Bieksa (2OT: Game 5 of 2011 CF w/ VAN) and Alec Martinez (2OT: Game 5 of 2014 SCF w/ LAK). -

Carolina Hurricanes
CAROLINA HURRICANES NEWS CLIPPINGS • May 7, 2021 Blackhawks rally late in regulation, beat Hurricanes in overtime By Chip Alexander “Today we just weren’t good enough,” Necas said. “We gave up so many chances against, and that just can’t happen. The Carolina Hurricanes played their last home game of the (Mrazek) made some big saves. We didn’t help him enough. regular season Thursday. We gave up too many Grade-A’s. They’ll soon be back, and for much bigger games. “We have to figure it out in the last two games. There’s no The Canes closed out their home schedule in this condensed way we can play like that in the playoffs.” season, facing the Chicago Blackhawks for the third time this Brind’Amour said Mrazek was the Canes’ “best player for week. For the first time this week, the Blackhawks won, sure” and was “great.” getting an overtime goal from Alex DeBrincat for a 2-1 victory. One of Mrazek’s biggest stops came just as the second period was ending when he stopped Patrick Kane on a Defenseman Riley Stillman tied the score 1-1 for the partial breakaway. DeBrincat had a breakaway earlier in the Blackhawks with 3:01 left in regulation with his first NHL second but couldn’t control the puck and didn’t get much on goal. Pius Suter turned near the left point and wristed a long- his shot. distance shot that Stillman tipped in the slot to beat goalie Petr Mrazek. “The first two periods, giving up breakaways, two-on-ones, breakaways, no coverage, it was just sloppy all over,” DeBrincat then whistled a shot from the slot past Vincent Brind’Amour said. -

Byfield ?Humbled? by OHL Rookie Honours
This page was exported from - The Auroran Export date: Mon Sep 27 11:37:17 2021 / +0000 GMT Byfield ?humbled? by OHL Rookie honours By Jake Courtepatte A familiar face around the Aurora rinks has been lauded as the top first-year player in the Ontario Hockey League. Former York-Simcoe Express captain Quinton Byfield was named on Thursday as the OHL's Rookie of the Year, earning the Emms Family Award for the 2018-19 season. ?It's super humbling,? said Byfield. ?There's a lot of good rookies this year that could have won it. I think a lot of them deserved it as well. I couldn't have done it by myself and owe a lot to my coaches who put trust in me, gave me every opportunity to succeed, and put me in every situation. He called his chemistry with his first-year teammates, both on and off the ice, ?unbelievable.? ?We had a very special group, we're super tight, and that helped us on the ice and really helped me too.? The Newmarket native, tabbed as a consensus first overall pick before even the midpoint of the 2017-18 season, was named the winner of the Jack Ferguson Trophy last April as the top choice by the Sudbury Wolves. The six-foot-four, 200 lb. centreman gained a reputation among the minor AAA circles as the right combination of speed and skill, captaining the Minor Midget Express to an OHL Output as PDF file has been powered by [ Universal Post Manager ] plugin from www.ProfProjects.com | Page 1/2 | This page was exported from - The Auroran Export date: Mon Sep 27 11:37:17 2021 / +0000 GMT Cup in March of 2018 while leading the team in scoring with 92 points. -

Ten #Nhlstats About the Carolina Hurricanes, Who
Ten #NHLStats about the Carolina Hurricanes, who are headed to the postseason for the third consecutive season and 16th time in franchise history (8x as Carolina, 8x as Hartford). 1. The Hurricanes have reached the playoffs in three consecutive seasons for the first time since moving to Raleigh in 1997-98 and second time in franchise history – the Whalers made seven straight appearances from 1986 to 1992. 2. Captain Jordan Staal leads all current Hurricanes players in career playoff goals (27), assists (19), points (46) and games played (96) and is one of three members of the roster with a Stanley Cup (2009 PIT). He can join his brother, Marc Staal (107 GP), as the second member of his family to skate in 100 career playoff games; only eight sets of brothers in League history have accomplished the feat. Their other brother, Eric Staal (now with the Canadiens), is the Hurricanes/Whalers franchise leader in career playoff goals (19), and points (43). 3. Cedric Paquette (2020 TBL) and Teuvo Teravainen (2015 CHI) are the other Hurricanes to win the Stanley Cup. Paquette will aim to become the second player in as many seasons, fourth in the NHL’s expansion era (since 1967-68) and ninth in League history to win a championship in consecutive seasons with different teams; he would be the second to do so by leaving the Lightning to join the Hurricanes (Cory Stillman). 4. Sebastian Aho has had 12 points in each of his first two trips to the postseason, pacing the club in scoring in both 2019 and 2020 (totaling 8-16—24 in 23 GP). -

Florida Panthers Game Notes
Florida Panthers Game Notes Tue, Mar 30, 2021 NHL Game #560 Florida Panthers 22 - 9 - 4 (48 pts) Detroit Red Wings 12 - 20 - 4 (28 pts) Team Game: 36 10 - 4 - 3 (Home) Team Game: 37 9 - 8 - 3 (Home) Home Game: 18 12 - 5 - 1 (Road) Road Game: 17 3 - 12 - 1 (Road) # Goalie GP W L OT GAA SV% # Goalie GP W L OT GAA SV% 60 Chris Driedger 15 9 4 2 2.19 .927 29 Thomas Greiss 21 2 14 4 3.51 .885 72 Sergei Bobrovsky 20 13 5 2 2.91 .903 31 Calvin Pickard 4 2 0 0 2.12 .904 36 Kaden Fulcher - - - - - - 45 Jonathan Bernier 17 8 6 0 2.78 .918 # P Player GP G A P +/- PIM # P Player GP G A P +/- PIM 3 D Keith Yandle 35 3 17 20 -7 30 3 D Alex Biega 3 0 0 0 -2 2 6 D Anton Stralman 29 3 6 9 -4 6 11 R Filip Zadina 29 3 10 13 -1 0 7 D Radko Gudas 34 0 5 5 10 25 14 C Robby Fabbri 27 10 8 18 6 14 10 R Brett Connolly 19 1 2 3 4 2 17 D Filip Hronek 36 2 18 20 -10 10 11 L Jonathan Huberdeau 35 13 27 40 -2 18 18 D Marc Staal 36 2 4 6 -3 14 13 C Vinnie Hinostroza 9 0 0 0 -2 0 22 D Patrik Nemeth 35 2 4 6 -6 14 16 C Aleksander Barkov 31 13 24 37 11 6 24 D Jon Merrill 30 0 4 4 4 6 19 L Mason Marchment 18 2 4 6 1 10 27 C Michael Rasmussen 20 1 4 5 -5 18 21 C Alex Wennberg 35 7 8 15 -1 8 37 R Evgeny Svechnikov 8 3 2 5 0 2 23 C Carter Verhaeghe 35 15 13 28 17 23 39 R Anthony Mantha 35 9 8 17 -13 17 27 C Eetu Luostarinen 34 3 5 8 -8 10 41 C Luke Glendening 34 3 6 9 0 10 42 D Gustav Forsling 22 2 3 5 1 6 43 L Darren Helm 27 1 3 4 -6 6 52 D MacKenzie Weegar 35 2 17 19 12 37 44 D Christian Djoos 30 2 6 8 -9 12 55 C Noel Acciari 27 3 7 10 3 4 48 R Givani Smith 8 1 3 4 0 11 -

At the PMC 550 Lansdowne St
HOME GAME 8 at the PMC 550 Lansdowne St. W 705-748-6200 @Marlin_Ptbo www.marlintravel.ca/1239 TABLE OF CONTENTS FAST FACTS 4 Petes vs. Wolves TAKING A CHANCE 5 ON DICK TODD CONFERENCE PETERBOROUGH 7 STANDINGS 10 PETES ROSTER SUDBURY LEAGUE 11 WOLVES ROSTER 15 LEADERS OFFICIAL GAMEDAY PROGRAM PAGE 3 Last Game (March 11/18): Petes 0 at Wolves 4 2017-18 Regular Season vs SBY: 3-1-0-0 Last Five Years vs SBY: 13-3-0-0 Last Five Years vs SBY on home ice: 7-1-0-0 LAST GAME TOP SCORERS taking a chance on todd PBO: 3-0 L @ NIAG PBO: Paquette - 14GP - 7G - 5A - 12P SBY: 2-0 W vs KGN SBY: Levin - 12GP - 5G - 6A - 11P How Dick todd went from a paper route to the nhl SPECIAL TEAMS The success of the Peterborough Petes and lengthy list of accomplished PBO: PP 10.9% (17th), PK 86.1% (5th) alumni reflect the remarkable group of coaches who have left their footprints SBY: PP 13.6% (15th), PK 83.7% (9th) on the organization. Among this group of men stands Dick Todd, whose time with the maroon and white poses a challenge to briefly summarize. After falling 3-0 to the IceDogs in Niagara last night, the Peterborough Petes are working to break an offensive slump to get back to their winning ways. They’ll do so Like many triumphant stories affiliated with the Petes, Todd’s begins against the Sudbury Wolves who are visiting the PMC for the first time this season. -

1998 SC Playoff Summaries
COLOR COLORADO AVALANCHE STANLEY CUP CHAMPIONS 2 0 0 1 David Aebischer, Rob Blake, Raymond Bourque, Greg de Vries, Chris Dingman, Chris Drury, Adam Foote, Peter Forsberg, Milan Hejduk, Dan Hinote, Jon Klemm, Eric Messier, Bryan Muir, Ville Nieminen, Scott Parker, Shjon Podein, Nolan Pratt, Dave Reid, Steve Reinprecht, Patrick Roy, Joe Sakic CAPTAIN, Martin Skoula, Alex Tanguay, Stephane Yelle E. Stanley Kroenke OWNER Pierre Lacroix GENERAL MANAGER, Bob Hartley HEAD COACH © Steve Lansky 2010 bigmouthsports.com NHL and the word mark and image of the Stanley Cup are registered trademarks and the NHL Shield and NHL Conference logos are trademarks of the National Hockey League. All NHL logos and marks and NHL team logos and marks as well as all other proprietary materials depicted herein are the property of the NHL and the respective NHL teams and may not be reproduced without the prior written consent of NHL Enterprises, L.P. Copyright © 2010 National Hockey League. All Rights Reserved. 0 2001 EASTERN CONFERENCE QUARTER-FINAL 1 NEW JERSEY DEVILS 111 v. 8 CAROLINA HURRICANES 88 GM LOU LAMORIELLO, HC LARRY ROBINSON v. GM JIM RUTHERFORD, HC PAUL MAURICE DEVILS WIN SERIES IN 6 Thursday, April 12 Sunday, April 15 (afternoon game) CAROLINA 1 @ NEW JERSEY 5 CAROLINA 0 @ NEW JERSEY 2 FIRST PERIOD FIRST PERIOD 1. NEW JERSEY, Sergei Brylin 1 (unassisted) 18:52 1. NEW JERSEY, Alexander Mogilny 1 (Sergei Brylin, Scott Gomez) 4:16 GWG Penalties — Hatcher C (holding stick) 4:58, R McKay N (goalie interference) 6:59, Tanabe C (tripping) 10:56 Penalties — Elias N (elbowing) 6:12, Karpa C (hooking) 19:07 SECOND PERIOD SECOND PERIOD 2. -

Colorado Avalanche Game Notes
Colorado Avalanche Game Notes Wed, Oct 30, 2019 NHL Game #191 Colorado Avalanche 8 - 2 - 1 (17 pts) Florida Panthers 5 - 3 - 4 (14 pts) Team Game: 12 4 - 1 - 0 (Home) Team Game: 13 2 - 1 - 1 (Home) Home Game: 6 4 - 1 - 1 (Road) Road Game: 9 3 - 2 - 3 (Road) # Goalie GP W L OT GAA SV% # Goalie GP W L OT GAA SV% 31 Philipp Grubauer 8 6 1 1 2.59 .920 33 Sam Montembeault 4 1 1 1 2.80 .905 39 Pavel Francouz 3 2 1 0 2.64 .926 72 Sergei Bobrovsky 10 4 2 3 3.79 .870 # P Player GP G A P +/- PIM # P Player GP G A P +/- PIM 6 D Erik Johnson 11 1 0 1 -2 4 2 D Josh Brown 11 1 1 2 -3 11 8 D Cale Makar 11 1 9 10 -1 0 3 D Keith Yandle 12 1 4 5 -1 2 11 L Matt Calvert 11 3 4 7 5 12 5 D Aaron Ekblad 11 1 5 6 1 4 12 C Jayson Megna - - - - - - 6 D Anton Stralman 12 0 4 4 -1 2 13 R Valeri Nichushkin 7 0 1 1 2 5 7 C Colton Sceviour 12 0 3 3 -1 2 16 D Nikita Zadorov 10 1 2 3 5 21 8 C Jayce Hawryluk 7 1 2 3 0 4 17 C Tyson Jost 11 4 1 5 1 6 9 C Brian Boyle 4 2 1 3 1 0 22 C Colin Wilson 9 0 4 4 6 0 10 R Brett Connolly 12 4 5 9 1 4 27 D Ryan Graves 11 1 1 2 5 4 11 L Jonathan Huberdeau 12 5 8 13 -4 8 28 D Ian Cole 7 0 5 5 11 8 13 D Mark Pysyk 7 1 1 2 -1 2 29 C Nathan MacKinnon 11 6 9 15 0 0 16 C Aleksander Barkov 12 0 13 13 -4 4 37 L J.T.