Boolean Algebra
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Propositional Logic (PDF)
Mathematics for Computer Science Proving Validity 6.042J/18.062J Instead of truth tables, The Logic of can try to prove valid formulas symbolically using Propositions axioms and deduction rules Albert R Meyer February 14, 2014 propositional logic.1 Albert R Meyer February 14, 2014 propositional logic.2 Proving Validity Algebra for Equivalence The text describes a for example, bunch of algebraic rules to the distributive law prove that propositional P AND (Q OR R) ≡ formulas are equivalent (P AND Q) OR (P AND R) Albert R Meyer February 14, 2014 propositional logic.3 Albert R Meyer February 14, 2014 propositional logic.4 1 Algebra for Equivalence Algebra for Equivalence for example, The set of rules for ≡ in DeMorgan’s law the text are complete: ≡ NOT(P AND Q) ≡ if two formulas are , these rules can prove it. NOT(P) OR NOT(Q) Albert R Meyer February 14, 2014 propositional logic.5 Albert R Meyer February 14, 2014 propositional logic.6 A Proof System A Proof System Another approach is to Lukasiewicz’ proof system is a start with some valid particularly elegant example of this idea. formulas (axioms) and deduce more valid formulas using proof rules Albert R Meyer February 14, 2014 propositional logic.7 Albert R Meyer February 14, 2014 propositional logic.8 2 A Proof System Lukasiewicz’ Proof System Lukasiewicz’ proof system is a Axioms: particularly elegant example of 1) (¬P → P) → P this idea. It covers formulas 2) P → (¬P → Q) whose only logical operators are 3) (P → Q) → ((Q → R) → (P → R)) IMPLIES (→) and NOT. The only rule: modus ponens Albert R Meyer February 14, 2014 propositional logic.9 Albert R Meyer February 14, 2014 propositional logic.10 Lukasiewicz’ Proof System Lukasiewicz’ Proof System Prove formulas by starting with Prove formulas by starting with axioms and repeatedly applying axioms and repeatedly applying the inference rule. -

Sets, Propositional Logic, Predicates, and Quantifiers
COMP 182 Algorithmic Thinking Sets, Propositional Logic, Luay Nakhleh Computer Science Predicates, and Quantifiers Rice University !1 Reading Material ❖ Chapter 1, Sections 1, 4, 5 ❖ Chapter 2, Sections 1, 2 !2 ❖ Mathematics is about statements that are either true or false. ❖ Such statements are called propositions. ❖ We use logic to describe them, and proof techniques to prove whether they are true or false. !3 Propositions ❖ 5>7 ❖ The square root of 2 is irrational. ❖ A graph is bipartite if and only if it doesn’t have a cycle of odd length. ❖ For n>1, the sum of the numbers 1,2,3,…,n is n2. !4 Propositions? ❖ E=mc2 ❖ The sun rises from the East every day. ❖ All species on Earth evolved from a common ancestor. ❖ God does not exist. ❖ Everyone eventually dies. !5 ❖ And some of you might already be wondering: “If I wanted to study mathematics, I would have majored in Math. I came here to study computer science.” !6 ❖ Computer Science is mathematics, but we almost exclusively focus on aspects of mathematics that relate to computation (that can be implemented in software and/or hardware). !7 ❖Logic is the language of computer science and, mathematics is the computer scientist’s most essential toolbox. !8 Examples of “CS-relevant” Math ❖ Algorithm A correctly solves problem P. ❖ Algorithm A has a worst-case running time of O(n3). ❖ Problem P has no solution. ❖ Using comparison between two elements as the basic operation, we cannot sort a list of n elements in less than O(n log n) time. ❖ Problem A is NP-Complete. -

From Fuzzy Sets to Crisp Truth Tables1 Charles C. Ragin
From Fuzzy Sets to Crisp Truth Tables1 Charles C. Ragin Department of Sociology University of Arizona Tucson, AZ 85721 USA [email protected] Version: April 2005 1. Overview One limitation of the truth table approach is that it is designed for causal conditions are simple presence/absence dichotomies (i.e., Boolean or "crisp" sets). Many of the causal conditions that interest social scientists, however, vary by level or degree. For example, while it is clear that some countries are democracies and some are not, there are many in-between cases. These countries are not fully in the set of democracies, nor are they fully excluded from this set. Fortunately, there is a well-developed mathematical system for addressing partial membership in sets, fuzzy-set theory. Section 2 of this paper provides a brief introduction to the fuzzy-set approach, building on Ragin (2000). Fuzzy sets are especially powerful because they allow researchers to calibrate partial membership in sets using values in the interval between 0 (nonmembership) and 1 (full membership) without abandoning core set theoretic principles, for example, the subset relation. Ragin (2000) demonstrates that the subset relation is central to the analysis of multiple conjunctural causation, where several different combinations of conditions are sufficient for the same outcome. While fuzzy sets solve the problem of trying to force-fit cases into one of two categories (membership versus nonmembership in a set), they are not well suited for conventional truth table analysis. With fuzzy sets, there is no simple way to sort cases according to the combinations of causal conditions they display because each case's array of membership scores may be unique. -

12 Propositional Logic
CHAPTER 12 ✦ ✦ ✦ ✦ Propositional Logic In this chapter, we introduce propositional logic, an algebra whose original purpose, dating back to Aristotle, was to model reasoning. In more recent times, this algebra, like many algebras, has proved useful as a design tool. For example, Chapter 13 shows how propositional logic can be used in computer circuit design. A third use of logic is as a data model for programming languages and systems, such as the language Prolog. Many systems for reasoning by computer, including theorem provers, program verifiers, and applications in the field of artificial intelligence, have been implemented in logic-based programming languages. These languages generally use “predicate logic,” a more powerful form of logic that extends the capabilities of propositional logic. We shall meet predicate logic in Chapter 14. ✦ ✦ ✦ ✦ 12.1 What This Chapter Is About Section 12.2 gives an intuitive explanation of what propositional logic is, and why it is useful. The next section, 12,3, introduces an algebra for logical expressions with Boolean-valued operands and with logical operators such as AND, OR, and NOT that Boolean algebra operate on Boolean (true/false) values. This algebra is often called Boolean algebra after George Boole, the logician who first framed logic as an algebra. We then learn the following ideas. ✦ Truth tables are a useful way to represent the meaning of an expression in logic (Section 12.4). ✦ We can convert a truth table to a logical expression for the same logical function (Section 12.5). ✦ The Karnaugh map is a useful tabular technique for simplifying logical expres- sions (Section 12.6). -

Lecture 1: Propositional Logic
Lecture 1: Propositional Logic Syntax Semantics Truth tables Implications and Equivalences Valid and Invalid arguments Normal forms Davis-Putnam Algorithm 1 Atomic propositions and logical connectives An atomic proposition is a statement or assertion that must be true or false. Examples of atomic propositions are: “5 is a prime” and “program terminates”. Propositional formulas are constructed from atomic propositions by using logical connectives. Connectives false true not and or conditional (implies) biconditional (equivalent) A typical propositional formula is The truth value of a propositional formula can be calculated from the truth values of the atomic propositions it contains. 2 Well-formed propositional formulas The well-formed formulas of propositional logic are obtained by using the construction rules below: An atomic proposition is a well-formed formula. If is a well-formed formula, then so is . If and are well-formed formulas, then so are , , , and . If is a well-formed formula, then so is . Alternatively, can use Backus-Naur Form (BNF) : formula ::= Atomic Proposition formula formula formula formula formula formula formula formula formula formula 3 Truth functions The truth of a propositional formula is a function of the truth values of the atomic propositions it contains. A truth assignment is a mapping that associates a truth value with each of the atomic propositions . Let be a truth assignment for . If we identify with false and with true, we can easily determine the truth value of under . The other logical connectives can be handled in a similar manner. Truth functions are sometimes called Boolean functions. 4 Truth tables for basic logical connectives A truth table shows whether a propositional formula is true or false for each possible truth assignment. -

Propositional Logic, Truth Tables, and Predicate Logic (Rosen, Sections 1.1, 1.2, 1.3) TOPICS
Propositional Logic, Truth Tables, and Predicate Logic (Rosen, Sections 1.1, 1.2, 1.3) TOPICS • Propositional Logic • Logical Operations • Equivalences • Predicate Logic Logic? What is logic? Logic is a truth-preserving system of inference Truth-preserving: System: a set of If the initial mechanistic statements are transformations, based true, the inferred on syntax alone statements will be true Inference: the process of deriving (inferring) new statements from old statements Proposi0onal Logic n A proposion is a statement that is either true or false n Examples: n This class is CS122 (true) n Today is Sunday (false) n It is currently raining in Singapore (???) n Every proposi0on is true or false, but its truth value (true or false) may be unknown Proposi0onal Logic (II) n A proposi0onal statement is one of: n A simple proposi0on n denoted by a capital leJer, e.g. ‘A’. n A negaon of a proposi0onal statement n e.g. ¬A : “not A” n Two proposi0onal statements joined by a connecve n e.g. A ∧ B : “A and B” n e.g. A ∨ B : “A or B” n If a connec0ve joins complex statements, parenthesis are added n e.g. A ∧ (B∨C) Truth Tables n The truth value of a compound proposi0onal statement is determined by its truth table n Truth tables define the truth value of a connec0ve for every possible truth value of its terms Logical negaon n Negaon of proposi0on A is ¬A n A: It is snowing. n ¬A: It is not snowing n A: Newton knew Einstein. n ¬A: Newton did not know Einstein. -

Valid Arguments
CHAPTER 3 Logic Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 3.7, Slide 1 3.7 Arguments and Truth Tables Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 3.7, Slide 2 Objectives 1. Use truth tables to determine validity. 2. Recognize and use forms of valid and invalid arguments. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 3.7, Slide 3 Arguments An Argument consists of two parts: Premises: the given statements. Conclusion: the result determined by the truth of the premises. Valid Argument: The conclusion is true whenever the premises are assumed to be true. Invalid Argument: Also called a fallacy Truth tables can be used to test validity. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 3.7, Slide 4 Testing the Validity of an Argument with a Truth Table Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 3.7, Slide 5 Example: Did the Pickiest Logician in the Galaxy Foul Up? In Star Trek, the spaceship Enterprise is hit by an ion storm, causing the power to go out. Captain Cook wonders if Mr. Scott is aware of the problem. Mr. Spock replies, “If Mr. Scott is still with us, the power should be on momentarily.” Moments later the ship’s power comes back on. Argument: If Mr. Scott is still with us, then the power will come on. The power comes on. Therefore, Mr. Scott is still with us. Determine whether the argument is valid or invalid. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 3.7, Slide 6 Example continued Solution Step 1: p: Mr. -
Logic and Truth Tables Truth Tables Are Logical Devices That Predominantly Show up in Mathematics, Computer Science, and Philosophy Applications
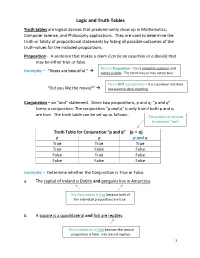
Logic and Truth Tables Truth tables are logical devices that predominantly show up in Mathematics, Computer Science, and Philosophy applications. They are used to determine the truth or falsity of propositional statements by listing all possible outcomes of the truth-values for the included propositions. Proposition - A sentence that makes a claim (can be an assertion or a denial) that may be either true or false. This is a Proposition – It is a complete sentence and Examples – “Roses are beautiful.” makes a claim. The claim may or may not be true. This is NOT a proposition – It is a question and does “Did you like the movie?” not assert or deny anything. Conjunction – an “and” statement. Given two propositions, p and q, “p and q” forms a conjunction. The conjunction “p and q” is only true if both p and q are true. The truth table can be set up as follows… This symbol can be used to represent “and”. Truth Table for Conjunction “p and q” (p ˄ q) p q p and q True True True True False False False True False False False False Examples – Determine whether the Conjunction is True or False. a. The capital of Ireland is Dublin and penguins live in Antarctica. This Conjunction is True because both of the individual propositions are true. b. A square is a quadrilateral and fish are reptiles. This Conjunction is False because the second proposition is false. Fish are not reptiles. 1 Disjunction – an “or” statement. Given two propositions, p and q, “p or q” forms a disjunction. -

Proposi'onal Logic Proofs Proof Method #1: Truth Table Example
9/9/14 Proposi'onal Logic Proofs • An argument is a sequence of proposi'ons: Inference Rules ² Premises (Axioms) are the first n proposi'ons (Rosen, Section 1.5) ² Conclusion is the final proposi'on. p p ... p q TOPICS • An argument is valid if is a ( 1 ∧ 2 ∧ ∧ n ) → tautology, given that pi are the premises • Logic Proofs (axioms) and q is the conclusion. ² via Truth Tables € ² via Inference Rules 2 Proof Method #1: Truth Table Example Proof By Truth Table s = ((p v q) ∧ (¬p v r)) → (q v r) n If the conclusion is true in the truth table whenever the premises are true, it is p q r ¬p p v q ¬p v r q v r (p v q)∧ (¬p v r) s proved 0 0 0 1 0 1 0 0 1 n Warning: when the premises are false, the 0 0 1 1 0 1 1 0 1 conclusion my be true or false 0 1 0 1 1 1 1 1 1 n Problem: given n propositions, the truth 0 1 1 1 1 1 1 1 1 n table has 2 rows 1 0 0 0 1 0 0 0 1 n Proof by truth table quickly becomes 1 0 1 0 1 1 1 1 1 infeasible 1 1 0 0 1 0 1 0 1 1 1 1 0 1 1 1 1 1 3 4 1 9/9/14 Proof Method #2: Rules of Inference Inference proper'es n A rule of inference is a pre-proved relaon: n Inference rules are truth preserving any 'me the leJ hand side (LHS) is true, the n If the LHS is true, so is the RHS right hand side (RHS) is also true. -

Foundations of Computation, Version 2.3.2 (Summer 2011)
Foundations of Computation Second Edition (Version 2.3.2, Summer 2011) Carol Critchlow and David Eck Department of Mathematics and Computer Science Hobart and William Smith Colleges Geneva, New York 14456 ii c 2011, Carol Critchlow and David Eck. Foundations of Computation is a textbook for a one semester introductory course in theoretical computer science. It includes topics from discrete mathematics, automata the- ory, formal language theory, and the theory of computation, along with practical applications to computer science. It has no prerequisites other than a general familiarity with com- puter programming. Version 2.3, Summer 2010, was a minor update from Version 2.2, which was published in Fall 2006. Version 2.3.1 is an even smaller update of Version 2.3. Ver- sion 2.3.2 is identical to Version 2.3.1 except for a change in the license under which the book is released. This book can be redistributed in unmodified form, or in mod- ified form with proper attribution and under the same license as the original, for non-commercial uses only, as specified by the Creative Commons Attribution-Noncommercial-ShareAlike 4.0 Li- cense. (See http://creativecommons.org/licenses/by-nc-sa/4.0/) This textbook is available for on-line use and for free download in PDF form at http://math.hws.edu/FoundationsOfComputation/ and it can be purchased in print form for the cost of reproduction plus shipping at http://www.lulu.com Contents Table of Contents iii 1 Logic and Proof 1 1.1 Propositional Logic ....................... 2 1.2 Boolean Algebra ....................... -

Part 2 Module 1 Logic: Statements, Negations, Quantifiers, Truth Tables
PART 2 MODULE 1 LOGIC: STATEMENTS, NEGATIONS, QUANTIFIERS, TRUTH TABLES STATEMENTS A statement is a declarative sentence having truth value. Examples of statements: Today is Saturday. Today I have math class. 1 + 1 = 2 3 < 1 What's your sign? Some cats have fleas. All lawyers are dishonest. Today I have math class and today is Saturday. 1 + 1 = 2 or 3 < 1 For each of the sentences listed above (except the one that is stricken out) you should be able to determine its truth value (that is, you should be able to decide whether the statement is TRUE or FALSE). Questions and commands are not statements. SYMBOLS FOR STATEMENTS It is conventional to use lower case letters such as p, q, r, s to represent logic statements. Referring to the statements listed above, let p: Today is Saturday. q: Today I have math class. r: 1 + 1 = 2 s: 3 < 1 u: Some cats have fleas. v: All lawyers are dishonest. Note: In our discussion of logic, when we encounter a subjective or value-laden term (an opinion) such as "dishonest," we will assume for the sake of the discussion that that term has been precisely defined. QUANTIFIED STATEMENTS The words "all" "some" and "none" are examples of quantifiers. A statement containing one or more of these words is a quantified statement. Note: the word "some" means "at least one." EXAMPLE 2.1.1 According to your everyday experience, decide whether each statement is true or false: 1. All dogs are poodles. 2. Some books have hard covers. 3. -

Truth Tables for Negation, Conjunction, and Disjunction
3.2 Truth Tables for Negation, Conjunction, and Disjunction Copyright © 2005 Pearson Education, Inc. Truth Table A truth table is used to determine when a compound statement is true or false. Copyright © 2005 Pearson Education, Inc. Slide 3-2 Conjunction Truth Table Click on speaker for audio The symbol ^ is read as “and” p q pq∧ Case 1 T T T Case 2 T F F Case 3 F T F Case 4 F F F The conjunction is true only when both p and q are true. Copyright © 2005 Pearson Education, Inc. Slide 3-3 Disjunction Click on speaker for audio The symbol V is read as “or” p q p ∨ q Case 1 T T T Case 2 T F T Case 3 F T T Case 4 F F F The disjunction is true when either p is true,qis true, or both p and q are true. Copyright © 2005 Pearson Education, Inc. Slide 3-4 Making a truth table Let’s construct a truth table for p v ~q. This is read as “p or not q”. Step 1: Make a table with different possibilities for p and q .There are 4 different possibilities. p q Case 1 T T Case 2 T F Case 3 F T Case 4 F F Copyright © 2005 Pearson Education, Inc. Slide 3-5 Making a truth table (cont’d) Click on speaker for audio Step 2: Now, make a column for ~q (“not” q) since we want to ultimately find p v ~q p q ~q Case 1 T T F Case 2 T F T Case 3 F T F Case 4 F F T Copyright © 2005 Pearson Education, Inc.