DOCSLIB.ORG

The Possible and the Actual in Phyllotaxis: Bridging the Gap Between Empirical Observations and Iterative Models

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Possible and the Actual in Phyllotaxis: Bridging the Gap Between Empirical Observations and Iterative Models The Possible and the Actual in Phyllotaxis: Bridging the Gap Between Empirical Observations and Iterative Models Scott Hotton1, Valerie Johnson2, Jessica Wilbarger 2, Kajetan Zwieniecki3, Pau Atela2, Christophe Golé2, Jacques Dumais3,* 1 UC Merced Center for Computational Biology, University of California, Merced CA 95344 2 Department of Mathematics, Smith College, Northampton MA 01063 3 Department of Organismic and Evolutionary Biology, Harvard University, Cambridge MA 02138 *Corresponding author; email [email protected], phone: 617 496-0751, fax: 617 496- 5945 ABSTRACT This paper presents new methods for the geometrical analysis of phyllotactic patterns and their comparison with patterns produced by simple, discrete dynamical systems. We introduce the concept of ontogenetic graph as a parsimonious and mechanistically relevant representation of a pattern. The ontogenetic graph is extracted from the local geometry of the pattern and does not impose large-scale regularity on it as for the divergence angle and other classical descriptors. We exemplify our approach by analyzing the phyllotaxis of two asteraceae in the light of a hard disk model. The simulated patterns offer a very good match to the observed patterns for over 150 iterations of the model. Key words: artichoke, Delaunay triangulation, dynamical system, shoot apical meristem, phyllotaxis, sunflower, Voronoi tessellation. INTRODUCTION Numerous patterns in Nature are made of identical units repeated regularly in space. Microtubules and viral capsids provide examples at the molecular level (Erickson 1973). Given that proteins and other macromolecules assemble over length scales that are only slightly larger than those of inorganic crystals it is not overly surprising that they offer similar patterns. However, when crystal-like regularity is found at the level of an entire living organism, one may justly be astonished. Yet, this is a common occurrence in plants where the arrangement of leaves and flowers around the stem, known as phyllotaxis, yields striking patterns (Figure 1). Figure 1. Crystal-like patterns in plants. (A) Bellis perennis, (B) broccoli romanesco (Brassica oleracea), (C) pine cone (Pinus sp). The symmetries found in crystals, biopolymers, and plants reflect two simple geometrical rules: i) equivalent or nearly equivalent units are added in succession and ii) the position of new units is determined by interactions with the units already in place. To visualize these rules in plants, one must focus on the shoot apical meristem where leaf and flower primordia are initiated in a stereotypical manner. It is commonly assumed that the divergence angle between successive primordia is close to the golden angle α = 360(2 − τ)o ≈137.5o where τ ≈1.608 is the golden mean (Figure 2). Repetition of the constant divergence angle over many primordia leads to the emergence of two families of spirals called parastichies (the two families are particularly clear in Figure 1C). The numbers of parastichies in these two families are often consecutive Fibonacci € numbers (1, 2, 3, 5, 8, 13, …). € Figure 2. Primordium initiation at the shoot apical meristem of Arabidopsis thaliana. Flower primordia are numbered according to their order of initiation and α is the divergence angle. The phenomenon of phyllotaxis raises at least two major questions - what is the nature of the interactions that determine the position of new primordia? and why, of all the possible patterns that can be created by repeating identical units in space, only a rather small set is ever seen in plants? The first question calls for experimental work to uncover the molecular, cellular and, potentially, mechanical factors that control the positioning of new primordia. The second question offers a different challenge since it presupposes some formal understanding of what patterns are possible whether or not these patterns are observed. To answer this question we need to build a bridge between the universe of observed phyllotactic patterns in plants and the more abstract universe of all patterns. We provide one of the first attempts to bridge the gap between the possible and the actual in phyllotaxis. The bridge rests on three pillars: i) a protocol to extract precise quantitative information from meristem images. ii) a dynamical system model that can be used to explore the universe of phyllotactic patterns. iii) a new concept, the ontogenetic graph, that provides the basis for comparing observed and simulated phyllotactic patterns. This paper is organized around these three contributions following a brief review of previous work in the area. For clarity, we discuss only patterns on a disk although our approach encompasses the whole breadth of phyllotactic patterns found in plants. PREVIOUS WORK The mechanistic basis of phyllotaxis has been reviewed by Jonsson and others (2006) in this issue; we therefore focus on the steps that have been made towards bridging the gap between the analysis of phyllotactic patterns in plants and their modeling via dynamical systems. Classical Geometric Models of Common Phyllotactic Patterns The classical geometric models of phyllotaxis all refer to lattices – either helices on a cylinder k (Atela and others 2002) or spirals on a disk. A spiral lattice is a set of points Pk = (ρ , kα), where α is the divergence angle and ρ is the plastochrone ratio (i.e. the ratio of radial distances for two successive primordia). The curve that joins these points ordered by k is called the ontogenetic spiral. The visible spirals in these patterns, joining each point to its nearest neighbors, are called parastichies. The parastichies are usually grouped in two families of parallel spirals (Figure 3). The number of parastichies in these families is the basis of the traditional classification of phyllotactic patterns. Figure 3. (A) A spiral lattice with parastichy numbers 11, 20. This is not a phyllotactic lattice as only one parastichy family can be formed with tangent disks. (B) A phyllotactic lattice, with parastichy numbers 13, 21. (C) The space of all lattice patterns as drawn by van Iterson in 1907. The tree structure is the subset of lattices corresponding to phyllotactic patterns. The longest branch shown corresponds to lattices with Fibonacci numbers. Lattices that are similar to patterns exhibited in plants are called phyllotactic lattices. Phyllotactic lattices can be represented by a collection of disks centered at the lattice points, with radii growing as βρk (for some β) and such that disks are tangent along two families of parastichies (compare Figure 3A and Figure 3B). The set of parameters yielding phyllotactic lattices was studied by van Iterson (1907) (Figure 3C) and forms a tree structure whose main branch contains all pairs (ρ, α) yielding lattices with Fibonacci parastichy numbers and converging toward the golden angle α ≈ 137.5o as ρ approaches 1. Dynamical Models of Phyllotaxis A large part of the literature offers geometric studies of models with no time evolution, involving only spiral configurations (Bravais and Bravais 1837; van Iterson 1907; Levitov 1991; Adler 1998). Unfortunately, they cannot explain the convergence to (and hence the stability of) regular spiral configurations from general initial conditions, nor can they account for plant patterns that are not lattices. In this paper, we use a geometric dynamical systems approach, as initiated in Atela and others (2002) (see also Kunz 1997; d’Ovidio and Mosekilde 2000). We were inspired by the iterative models of the physicists Douady and Couder (1996) (see also the related systems proposed by Schwabe and Clewer 1984; Koch and others 1998): they are sufficiently simple to be cast as discrete dynamical systems; yet, they are compatible with most of the biological mechanisms proposed such as buckling and auxin transport. These dynamical systems models are an implementation of the two rules stated in the introduction, as applied to phyllotaxis. More specifically: 1) Primordia are formed successively in time 2) Primordia are positioned in the “least crowded spot” at the edge of the meristem If one assumes that primordia form with fixed period, one obtains what Douady and Couder called the Hofmeister hypothesis. If one assumes that new primordia form when and where there is enough space, one obtains the so-called Snow hypothesis. The Snow hypothesis has the advantage of allowing simultaneous formation of several primordia (sometimes yielding multijugate configurations). Douady and Couder (1996) numerically reproduced many features of the van Iterson diagram. They also showed that, for a given set of parameters, configurations starting with different initial conditions could converge to either spiral or whorl configurations. This result suggests that the initial configuration of primordia found in the meristem of the plant seedling could play an important role in determining the phyllotaxis later in development. Mathematically, these models can be seen as discrete dynamical systems acting on points (R0,θ0 ),...,(RN ,θN ) of the disk (each point representing the center of a primordium in polar coordinates) with a transformation from one configuration to the next of the form: (R0,θ0,...,RN ,θN ) → ( f (R0,θ0,...,RN ,θN ),R0,θ0,...,RN−1,θN−1), where the function f determines the location of the new primordium that minimizes its interaction € with the existing ones. € The Hofmeister type models have pre-established plastochrone ratio ρ = Rk /Rk-1 so that R needs not be explicitly part of the transformation above. In the Snow-type models, f expresses the location and time at which the interaction W falls below a certain threshold. In either case, most authors consider an interaction of the form W (R,θ,R0,R0,...,RN ,θN ) = ∑u(R,θ,Rk,θk ), k where (R,θ) is the test location of the new primordium and u is a more or less explicit function of a the distance between (Rk,θk) and (R,θ). Douady and Couder used, among others, u = c dis where a and c are constants and dis means distance between (R ,θ ) and (R,θ). Our group has € k k € € proposed, in either the Hofmeister or Snow models (Atela and others 2002; Atela and Golé 2006) a radical simplification of the interaction as * W (R,θ,R0,θ0,...,RN ,θN ) = maxk u(R,θ,Rk,θk ).
Load more

Recommended publications
  • Title: Fractals Topics: Symmetry, Patterns in Nature, Biomimicry Related Disciplines: Mathematics, Biology Objectives: A. Learn
    Title: Fractals Topics: symmetry, patterns in nature, biomimicry Related Disciplines: mathematics, biology Objectives: A. Learn about how fractals are made. B. Think about the mathematical processes that play out in nature. C. Create a hands-on art project. Lesson: A. Introduction (20 minutes) Fractals are sets in mathematics based on repeated processes at different scales. Why do we care? Fractals are a part of nature, geometry, algebra, and science and are beautiful in their complexity. Fractals come in many types: branching, spiral, algebraic, and geometric. Branching and spiral fractals can be found in nature in many different forms. Branching is seen in trees, lungs, snowflakes, lightning, and rivers. Spirals are visible in natural forms such as hurricanes, shells, liquid motion, galaxies, and most easily visible in plants like flowers, cacti, and Romanesco Figure 1: Romanesco (Figure 1). Branching fractals emerge in a linear fashion. Spirals begin at a point and expand out in a circular motion. A cool demonstration of branching fractals can be found at: http://fractalfoundation.org/resources/what-are-fractals/. Algebraic fractals are based on surprisingly simple equations. Most famous of these equations is the Mandelbrot Set (Figure 2), a plot made from the equation: The most famous of the geometric fractals is the Sierpinski Triangle: As seen in the diagram above, this complex fractal is created by starting with a single triangle, then forming another inside one quarter the size, then three more, each one quarter the size, then 9, 27, 81, all just one quarter the size of the triangle drawn in the previous step.
    [Show full text]
  • 6 Phyllotaxis in Higher Plants Didier Reinhardt and Cris Kuhlemeier
    6 Phyllotaxis in higher plants Didier Reinhardt and Cris Kuhlemeier 6.1 Introduction In plants, the arrangement of leaves and flowers around the stem is highly regular, resulting in opposite, alternate or spiral arrangements.The pattern of the lateral organs is called phyllotaxis, the Greek word for ‘leaf arrangement’. The most widespread phyllotactic arrangements are spiral and distichous (alternate) if one organ is formed per node, or decussate (opposite) if two organs are formed per node. In flowers, the organs are frequently arranged in whorls of 3-5 organs per node. Interestingly, phyllotaxis can change during the course of develop- ment of a plant. Usually, such changes involve the transition from decussate to spiral phyllotaxis, where they are often associated with the transition from the vegetative to reproductive phase. Since the first descriptions of phyllotaxis, the apparent regularity, especially of spiral phyllotaxis, has attracted the attention of scientists in various dis- ciplines. Philosophers and natural scientists were among the first to consider phyllotaxis and to propose models for its regulation. Goethe (1 830), for instance, postulated the existence of a general ‘spiral tendency in plant vegetation’. Mathematicians have described the regularity of phyllotaxis (Jean, 1994), and developed computer models that can recreate phyllotactic patterns (Meinhardt, 1994; Green, 1996). It was recognized early that phyllotactic patterns are laid down in the shoot apical meristem, the site of organ formation. Since scientists started to pos- tulate mechanisms for the regulation of phyllotaxis, two main concepts have dominated the field. The first principle holds that the geometry of the apex, and biophysical forces in the meristem determine phyllotaxis (van Iterson, 1907; Schiiepp, 1938; Snow and Snow, 1962; Green, 1992, 1996).
    [Show full text]
  • Branching in Nature Jennifer Welborn Amherst Regional Middle School, [email protected]
    University of Massachusetts Amherst ScholarWorks@UMass Amherst Patterns Around Us STEM Education Institute 2017 Branching in Nature Jennifer Welborn Amherst Regional Middle School, [email protected] Wayne Kermenski Hawlemont Regional School, [email protected] Follow this and additional works at: https://scholarworks.umass.edu/stem_patterns Part of the Biology Commons, Physics Commons, Science and Mathematics Education Commons, and the Teacher Education and Professional Development Commons Welborn, Jennifer and Kermenski, Wayne, "Branching in Nature" (2017). Patterns Around Us. 2. Retrieved from https://scholarworks.umass.edu/stem_patterns/2 This Article is brought to you for free and open access by the STEM Education Institute at ScholarWorks@UMass Amherst. It has been accepted for inclusion in Patterns Around Us by an authorized administrator of ScholarWorks@UMass Amherst. For more information, please contact [email protected]. Patterns Around Us: Branching in Nature Teacher Resource Page Part A: Introduction to Branching Massachusetts Frameworks Alignment—The Nature of Science • Overall, the key criterion of science is that it provide a clear, rational, and succinct account of a pattern in nature. This account must be based on data gathering and analysis and other evidence obtained through direct observations or experiments, reflect inferences that are broadly shared and communicated, and be accompanied by a model that offers a naturalistic explanation expressed in conceptual, mathematical, and/or mechanical terms. Materials:
    [Show full text]
  • Multidimensional Generalization of Phyllotaxis
    CYBERNETICS AND PHYSICS, VOL. 8, NO. 3, 2019, 153–160 MULTIDIMENSIONAL GENERALIZATION OF PHYLLOTAXIS Andrei Lodkin Dept. of Mathematics & Mechanics St. Petersburg State University Russia [email protected] Article history: Received 28.10.2019, Accepted 28.11.2019 Abstract around a stem, seeds on a pine cone or a sunflower head, The regular spiral arrangement of various parts of bi- florets, petals, scales, and other units usually shows a ological objects (leaves, florets, etc.), known as phyl- regular character, see the pictures below. lotaxis, could not find an explanation during several cen- turies. Some quantitative parameters of the phyllotaxis (the divergence angle being the principal one) show that the organization in question is, in a sense, the same in a large family of living objects, and the values of the divergence angle that are close to the golden number prevail. This was a mystery, and explanations of this phenomenon long remained “lyrical”. Later, similar pat- terns were discovered in inorganic objects. After a se- ries of computer models, it was only in the XXI cen- tury that the rigorous explanation of the appearance of the golden number in a simple mathematical model has been given. The resulting pattern is related to stable fixed points of some operator and depends on a real parame- ter. The variation of this parameter leads to an inter- esting bifurcation diagram where the limiting object is the SL(2; Z)-orbit of the golden number on the segment [0,1]. We present a survey of the problem and introduce a multidimensional analog of phyllotaxis patterns.
    [Show full text]
  • Art on a Cellular Level Art and Science Educational Resource
    Art on a Cellular Level Art and Science Educational Resource Phoenix Airport Museum Educators and Parents, With foundations in art, geometry and plant biology, the objective of this lesson is to recognize patterns and make connections between the inexhaustible variety of life on our planet. This educational resource is geared for interaction with students of all ages to support the understanding between art and science. It has been designed based on our current exhibition, Art on a Cellular Level, on display at Sky Harbor. The questions and activities below were created to promote observation and curiosity. There are no wrong answers. You may print this PDF to use as a workbook or have your student refer to the material online. We encourage educators to expand on this art and science course to create a lesson plan. If you enjoy these activities and would like to investigate further, check back for new projects each week (three projects total). We hope your student will have fun with this and make an art project to share with us. Please send an image of your student’s artwork to [email protected] or hashtag #SkyHarborArts for an opportunity to be featured on Phoenix Sky Harbor International Airport’s social media. Art on a Cellular Level exhibition Sky Harbor, Terminal 4, level 3 Gallery Art is a lens through which we view the world. It can be a tool for storytelling, expressing cultural values and teaching fundamentals of math, technology and science in a visual way. The Terminal 4 gallery exhibition, Art on a Cellular Level, examines the intersections between art and science.
    [Show full text]
  • A Method of Constructing Phyllotaxically Arranged Modular Models by Partitioning the Interior of a Cylinder Or a Cone
    A method of constructing phyllotaxically arranged modular models by partitioning the interior of a cylinder or a cone Cezary St¸epie´n Institute of Computer Science, Warsaw University of Technology, Poland [email protected] Abstract. The paper describes a method of partitioning a cylinder space into three-dimensional sub- spaces, congruent to each other, as well as partitioning a cone space into subspaces similar to each other. The way of partitioning is of such a nature that the intersection of any two subspaces is the empty set. Subspaces are arranged with regard to phyllotaxis. Phyllotaxis lets us distinguish privileged directions and observe parastichies trending these directions. The subspaces are created by sweeping a changing cross-section along a given path, which enables us to obtain not only simple shapes but also complicated ones. Having created these subspaces, we can put modules inside them, which do not need to be obligatorily congruent or similar. The method ensures that any module does not intersect another one. An example of plant model is given, consisting of modules phyllotaxically arranged inside a cylinder or a cone. Key words: computer graphics; modeling; modular model; phyllotaxis; cylinder partitioning; cone partitioning; genetic helix; parastichy. 1. Introduction Phyllotaxis is the manner of how leaves are arranged on a plant stem. The regularity of leaves arrangement, known for a long time, still absorbs the attention of researchers in the fields of botany, mathematics and computer graphics. Various methods have been used to describe phyllotaxis. A historical review of problems referring to phyllotaxis is given in [7]. Its connections with number sequences, e.g.
    [Show full text]
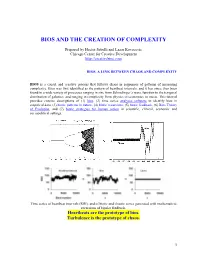
  • Bios and the Creation of Complexity
    BIOS AND THE CREATION OF COMPLEXITY Prepared by Hector Sabelli and Lazar Kovacevic Chicago Center for Creative Development http://creativebios.com BIOS, A LINK BETWEEN CHAOS AND COMPLEXITY BIOS is a causal and creative process that follows chaos in sequences of patterns of increasing complexity. Bios was first identified as the pattern of heartbeat intervals, and it has since then been found in a wide variety of processes ranging in size from Schrodinger’s wave function to the temporal distribution of galaxies, and ranging in complexity from physics to economics to music. This tutorial provides concise descriptions of (1) bios, (2) time series analyses software to identify bios in empirical data, (3) biotic patterns in nature, (4) biotic recursions, (5) biotic feedback, (6) Bios Theory of Evolution, and (7) biotic strategies for human action in scientific, clinical, economic and sociopolitical settings. Time series of heartbeat intervals (RRI), and of biotic and chaotic series generated with mathematical recursions of bipolar feedback. Heartbeats are the prototype of bios. Turbulence is the prototype of chaos. 1 1. BIOS BIOS is an expansive process with chaotic features generated by feedback and characterized by features of creativity. Process: Biotic patterns are sequences of actions or states. Expansive: Biotic patterns continually expand in their diversity and often in their range. This is significant, as natural processes expand, in contrast to convergence to equilibrium, periodic, or chaotic attractors. Expanding processes range from the universe to viruses, and include human populations, empires, ideas and cultures. Chaotic: Biotic series are aperiodic and generated causally; mathematically generated bios is extremely sensitive to initial conditions.
    [Show full text]
  • Phyllotaxis: a Remarkable Example of Developmental Canalization in Plants Christophe Godin, Christophe Golé, Stéphane Douady
    Phyllotaxis: a remarkable example of developmental canalization in plants Christophe Godin, Christophe Golé, Stéphane Douady To cite this version: Christophe Godin, Christophe Golé, Stéphane Douady. Phyllotaxis: a remarkable example of devel- opmental canalization in plants. 2019. hal-02370969 HAL Id: hal-02370969 https://hal.archives-ouvertes.fr/hal-02370969 Preprint submitted on 19 Nov 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Phyllotaxis: a remarkable example of developmental canalization in plants Christophe Godin, Christophe Gol´e,St´ephaneDouady September 2019 Abstract Why living forms develop in a relatively robust manner, despite various sources of internal or external variability, is a fundamental question in developmental biology. Part of the answer relies on the notion of developmental constraints: at any stage of ontogenenesis, morphogenetic processes are constrained to operate within the context of the current organism being built, which is thought to bias or to limit phenotype variability. One universal aspect of this context is the shape of the organism itself that progressively channels the development of the organism toward its final shape. Here, we illustrate this notion with plants, where conspicuous patterns are formed by the lateral organs produced by apical meristems.
    [Show full text]
  • Phyllotaxis: a Model
    Phyllotaxis: a Model F. W. Cummings* University of California Riverside (emeritus) Abstract A model is proposed to account for the positioning of leaf outgrowths from a plant stem. The specified interaction of two signaling pathways provides tripartite patterning. The known phyllotactic patterns are given by intersections of two ‘lines’ which are at the borders of two determined regions. The Fibonacci spirals, the decussate, distichous and whorl patterns are reproduced by the same simple model of three parameters. *present address: 136 Calumet Ave., San Anselmo, Ca. 94960; [email protected] 1 1. Introduction Phyllotaxis is the regular arrangement of leaves or flowers around a plant stem, or on a structure such as a pine cone or sunflower head. There have been many models of phyllotaxis advanced, too numerous to review here, but a recent review does an admirable job (Kuhlemeier, 2009). The lateral organs are positioned in distinct patterns around the cylindrical stem, and this alone is often referred to phyllotaxis. Also, often the patterns described by the intersections of two spirals describing the positions of florets such as (e.g.) on a sunflower head, are included as phyllotactic patterns. The focus at present will be on the patterns of lateral outgrowths on a stem. The patterns of intersecting spirals on more flattened geometries will be seen as transformations of the patterns on a stem. The most common patterns on a stem are the spiral, distichous, decussate and whorled. The spirals must include especially the common and well known Fibonacci patterns. Transition between patterns, for instance from decussate to spiral, is common as the plant grows.
    [Show full text]
  • Spiral Phyllotaxis: the Natural Way to Construct a 3D Radial Trajectory in MRI
    Magnetic Resonance in Medicine 66:1049–1056 (2011) Spiral Phyllotaxis: The Natural Way to Construct a 3D Radial Trajectory in MRI Davide Piccini,1* Arne Littmann,2 Sonia Nielles-Vallespin,2 and Michael O. Zenge2 While radial 3D acquisition has been discussed in cardiac MRI methods feature properties that are particularly well suited for its excellent results with radial undersampling, the self- for cardiac MRI applications. navigating properties of the trajectory need yet to be exploited. In the field of cardiac MRI, it has to be considered that Hence, the radial trajectory has to be interleaved such that the anatomy of the heart is very complex. Furthermore, the first readout of every interleave starts at the top of the sphere, which represents the shell covering all readouts. If this in many cases, the location and orientation of the heart is done sub-optimally, the image quality might be degraded by differ individually within the thorax. Up to now, only eddy current effects, and advanced density compensation is experienced operators are able to perform a comprehen- needed. In this work, an innovative 3D radial trajectory based on sive cardiac MR examination. As a consequence, the option a natural spiral phyllotaxis pattern is introduced, which features to acquire a 3D volume that covers the whole heart with optimized interleaving properties: (1) overall uniform readout high and isotropic resolution is a much desirable goal (11). distribution is preserved, which facilitates simple density com- In this configuration, some of the preparatory steps of a pensation, and (2) if the number of interleaves is a Fibonacci cardiac examination are obsolete since the complexity of number, the interleaves self-arrange such that eddy current effects are significantly reduced.
    [Show full text]
  • Pattern Formation in Nature: Physical Constraints and Self-Organising Characteristics
    Pattern formation in nature: Physical constraints and self-organising characteristics Philip Ball ________________________________________________________________ Abstract The formation of patterns is apparent in natural systems ranging from clouds to animal markings, and from sand dunes to the intricate shells of microscopic marine organisms. Despite the astonishing range and variety of such structures, many seem to have analogous features: the zebra’s stripes put us in mind of the ripples of blown sand, for example. In this article I review some of the common patterns found in nature and explain how they are typically formed through simple, local interactions between many components of a system – a form of physical computation that gives rise to self- organisation and emergent structures and behaviours. ________________________________________________________________ Introduction When the naturalist Joseph Banks first encountered Fingal’s Cave on the Scottish island of Staffa, he was astonished by the quasi-geometric, prismatic pillars of rock that flank the entrance. As Banks put it, Compared to this what are the cathedrals or palaces built by men! Mere models or playthings, as diminutive as his works will always be when compared with those of nature. What now is the boast of the architect! Regularity, the only part in which he fancied himself to exceed his mistress, Nature, is here found in her possession, and here it has been for ages undescribed. This structure has a counterpart on the coast of Ireland: the Giant’s Causeway in County Antrim, where again one can see the extraordinarily regular and geometric honeycomb structure of the fractured igneous rock (Figure 1). When we make an architectural pattern like this, it is through careful planning and construction, with each individual element cut to shape and laid in place.
    [Show full text]
  • Dynamical System Approach to Phyllotaxis
    Downloaded from orbit.dtu.dk on: Dec 17, 2017 Dynamical system approach to phyllotaxis D'ovidio, Francesco; Mosekilde, Erik Published in: Physical Review E. Statistical, Nonlinear, and Soft Matter Physics Link to article, DOI: 10.1103/PhysRevE.61.354 Publication date: 2000 Document Version Publisher's PDF, also known as Version of record Link back to DTU Orbit Citation (APA): D'ovidio, F., & Mosekilde, E. (2000). Dynamical system approach to phyllotaxis. Physical Review E. Statistical, Nonlinear, and Soft Matter Physics, 61(1), 354-365. DOI: 10.1103/PhysRevE.61.354 General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. PHYSICAL REVIEW E VOLUME 61, NUMBER 1 JANUARY 2000 Dynamical system approach to phyllotaxis F. d’Ovidio1,2,* and E. Mosekilde1,† 1Center for Chaos and Turbulence Studies, Building 309, Department of Physics, Technical University of Denmark, 2800 Lyngby, Denmark 2International Computer Science Institute, 1947 Center Street, Berkeley, California 94704-1198 ͑Received 13 August 1999͒ This paper presents a bifurcation study of a model widely used to discuss phyllotactic patterns, i.e., leaf arrangements.
    [Show full text]