DOCSLIB.ORG

The Lyx User's Guide

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Lyx User's Guide Interest-rate Models: an Extension to the Usage in the Energy Market and Pricing Exotic Energy Derivatives Dan Wang Supervisor: Professor Nigel Meade Center for Quantitative Finance The Business School Imperial College of Science, Technology and Medicine In partial fulfillment of the requirements for the degree of Doctor of Philosophy May, 2009 Abstract In this thesis, we review various popular pricing models in the interest-rate market. Among these pricing models, we choose the LIBOR Market model (LMM) as the benchmark model. Based on market practice experience, we also develop a pricing model named the “Market volatility model”. By pricing vanilla interest-rate options such as interest-rate caps and swaptions, we compare the performance of our Market volatility model to that of the LMM. It is proved that the Market Volatility model produce comparable results to the LMM, while its computing efficiency largely exceeds that of the LMM. Following the recent rapid development in the commodity market, in particular the energy market, we attempt to extend the use of our proposed Market volatility model from the interest-rate market to the energy market. We prove that the Market Volatility model is capable of pricing various energy derivative under the assumption of absence of the convenience yield. In addition, we propose a new type of exotic energy derivative which has a flexible option structure. This energy derivative is named as the Flex-Asian spread options (FASO). We give examples of different option structures within the FASO framework and use the Market volatility model to generate option prices and greeks for each structure. Although the Market volatility model can be used to price various energy derivatives based on oil/gas contracts, it is not compatible with the structure of one of the most advanced derivatives in the energy market, the storage option. We modify the existing pricing model for storage options and use our own 3D-binomial tree approach to price gas storage contracts. By doing these, we improve the performance of the traditional storage model. ii Acknowledgment I would like to thank my supervisor, Professor Nigel Meade and Professor Nicos Christofides, for their guidance through my PhD research and the writing of this thesis. I would also like to thank my current manager Philip Atkins at BP and my previous manager Maarten Wiersinga at Mizuho International, for offering me the invaluable opportunity to work in their teams. Thanks to all my previous and current colleagues from the Risk Quantitative Analysis team at BP and the Model Validation team at Mizuho respectively, for helping me to learn practical knowledge in the financial markets. I would like to thank all my previous teacher, friends and colleagues, for those of you who have helped me at work and in life. In particular, I would like to thank Yukun Shen, for all your invaluable inspirations and help when I worked on this thesis. I would also like to thank Lin Luo, for bringing up the idea of pursuing a PhD at CQF; Maggie Zhang and Carole Ye, for providing great help when I was working at Mizuho; Jing Wei, for the on-going support and being there whenever I was in need. I would like to thank my parents, who encourage me to face the challenges along the years of my PhD. Without your guidance and support, I could achieve nothing today. After all those years, I guess I have finally made some effort and I just wish I could make you proud. This thesis is dedicated to my parents with my love. iii Contents 1. Introduction 8 2. Interest-Rate Models 11 2.1. The LIBOR Market Model................................ 11 2.1.1. The Heath-Jarrow-Morton (HJM) framework.................. 12 2.1.2. Log-normal LIBOR Models............................ 14 2.1.2.1. Determining the No-Arbitrage Drifts of Forward Rates....... 14 2.1.2.2. The Miltersen-Sandmann-Sondermann Approach........... 18 2.1.2.3. The Brace-Gatarek-Musiela Approach................. 18 2.1.2.4. The Musiela-Rutkowski Approach................... 20 2.1.3. Descriptions of the Forward Rate Dynamics of the LIBOR Market Model.. 24 2.1.3.1. The First Description of Forward LIBOR Rates........... 24 2.1.3.2. The Second Description of Forward LIBOR Rates.......... 25 2.1.3.3. The Third Description of Forward LIBOR Rates........... 26 2.1.3.4. Principal Component Analysis (PCA)................. 27 2.1.4. Finding the Suitable Functional Forms for Instantaneous Volatilities..... 28 2.1.5. Calibration of the Caplet and Swaption Volatilities in LMM.......... 31 2.1.5.1. Calibration for Caplet Volatilities................... 32 2.1.5.2. Calibration for European Swaption Volatilities............ 33 2.1.6. Calibration for Instantaneous Correlations.................... 34 2.1.7. Incompatibility between the LSM and the LFM................ 37 2.2. The Stochastic-αβρ (SABR) model............................ 38 2.2.1. The Stochastic-β Model Framework....................... 38 2.2.1.1. Implied Normal Volatility....................... 39 2.2.1.2. Implied Black Volatility......................... 39 2.2.2. Pricing Formula for a Vanilla Call Option.................... 40 2.3. The CIR-Jump model................................... 40 2.4. The Market Volatility Model............................... 42 2.4.1. Interpolation of the Piecewise-Constant Volatilities of Forward Rates..... 43 2.4.1.1. The “Stripping” Method for the Caplet Volatilities......... 43 2.4.1.2. The Bi-linear Interpolation for the Swaption Volatilities....... 45 2.4.2. The link between the Market Volatility Model and the Implied Trinomial Tree Method.................................... 47 2.5. Summary.......................................... 48 iv Contents 3. Pricing Interest-rate Options 50 3.1. European-style Interest-Rate Options........................... 50 3.1.1. Interest-Rate Caps/Floors............................. 50 3.1.2. European Swaptions................................ 52 3.2. Exotic Interest-Rate Options............................... 53 3.2.1. Constant Maturity Swaps............................. 53 3.2.2. CMS Spread Options................................ 55 3.3. Performance of LMM v.s. the Market Volatility Model................. 56 3.3.1. European Swaptions................................ 56 3.3.2. Caps......................................... 63 3.4. Pricing Exotic Interest-Rate Options Using the Market Volatility Model....... 67 3.5. Summary.......................................... 71 4. From the Interest-Rate Market to the Energy Market 73 4.1. Introduction of the Energy Market............................ 73 4.1.1. The Oil Market................................... 73 4.1.2. The Natural Gas Market............................. 74 4.2. The Spot-Forward Relationship in the Energy/Commodity Market.......... 76 4.3. Common Pricing Models in the Energy Market..................... 79 4.3.1. The Bachelier Model............................... 79 4.3.2. The Black-Scholes Model............................. 79 4.3.3. The Mean-Reverting Model............................ 80 4.3.4. The Jump-Diffusion Model............................ 80 4.3.5. The Stochastic Volatility Model.......................... 81 4.4. The Market Volatility Model for the Energy Market.................. 81 4.5. Summary.......................................... 82 5. Pricing Exotic Energy Options 83 5.1. Spread Options....................................... 83 5.2. Basket Options....................................... 84 5.3. Asian Options........................................ 84 5.4. Flex-Asian Spread Options (FASO)............................ 85 5.4.1. The FASO Type-1 Option............................. 86 5.4.2. The FASO Type-2 Option............................. 86 5.4.3. The FASO Type-3 Option............................. 87 5.4.4. The FASO Type-4 Option............................. 88 5.5. Test Scenarios for FASO.................................. 89 5.5.1. Moneyness Definition............................... 89 5.5.2. Structures of the Pricing Windows in FASO................... 91 5.5.3. Correlation Matrices................................ 95 5.5.4. Volatilities..................................... 96 5.5.5. Test Results..................................... 96 5.6. Summary.......................................... 101 v Contents 6. The Storage Model 103 6.1. The Intuition Behind the Development of Storage Option Pricing Models...... 103 6.2. Various Methods for Valuing a Storage Contract.................... 104 6.2.1. The Rolling Intrinsic Method........................... 106 6.2.2. The Trinomial Tree Forest Method........................ 107 6.2.3. The Basket of Spread Options Method...................... 107 6.2.3.1. The Rolling Basket of Spread Options Method............ 108 6.2.4. The Least Squares Monte-Carlo Method..................... 109 6.3. The Storage Model Methodology............................. 111 6.3.1. Brief Introduction of the Calibration Process.................. 112 6.3.2. Modeling volatilities................................ 113 6.3.3. Modeling correlation................................ 118 6.3.3.1. Local Correlation............................ 118 6.3.3.2. Term Correlation............................ 119 6.3.3.3. Cash Correlation............................. 119 6.3.3.4. Correlation Analysis........................... 120 6.3.4. Calendar Spread Option Pricing Model..................... 123 6.3.5. The Analytic Formulas of Spread Option Greeks for the Storage Model... 124 6.3.6. Linear Programming Problem........................... 126 6.4. Storage values.......................................
Load more

Recommended publications
  • Trinomial Tree
    Trinomial Tree • Set up a trinomial approximation to the geometric Brownian motion dS=S = r dt + σ dW .a • The three stock prices at time ∆t are S, Su, and Sd, where ud = 1. • Impose the matching of mean and that of variance: 1 = pu + pm + pd; SM = (puu + pm + (pd=u)) S; 2 2 2 2 S V = pu(Su − SM) + pm(S − SM) + pd(Sd − SM) : aBoyle (1988). ⃝c 2013 Prof. Yuh-Dauh Lyuu, National Taiwan University Page 599 • Above, M ≡ er∆t; 2 V ≡ M 2(eσ ∆t − 1); by Eqs. (21) on p. 154. ⃝c 2013 Prof. Yuh-Dauh Lyuu, National Taiwan University Page 600 * - pu* Su * * pm- - j- S S * pd j j j- Sd - j ∆t ⃝c 2013 Prof. Yuh-Dauh Lyuu, National Taiwan University Page 601 Trinomial Tree (concluded) • Use linear algebra to verify that ( ) u V + M 2 − M − (M − 1) p = ; u (u − 1) (u2 − 1) ( ) u2 V + M 2 − M − u3(M − 1) p = : d (u − 1) (u2 − 1) { In practice, we must also make sure the probabilities lie between 0 and 1. • Countless variations. ⃝c 2013 Prof. Yuh-Dauh Lyuu, National Taiwan University Page 602 A Trinomial Tree p • Use u = eλσ ∆t, where λ ≥ 1 is a tunable parameter. • Then ( ) p r + σ2 ∆t ! 1 pu 2 + ; 2λ ( 2λσ) p 1 r − 2σ2 ∆t p ! − : d 2λ2 2λσ p • A nice choice for λ is π=2 .a aOmberg (1988). ⃝c 2013 Prof. Yuh-Dauh Lyuu, National Taiwan University Page 603 Barrier Options Revisited • BOPM introduces a specification error by replacing the barrier with a nonidentical effective barrier.
    [Show full text]
  • A Fuzzy Real Option Model for Pricing Grid Compute Resources
    A Fuzzy Real Option Model for Pricing Grid Compute Resources by David Allenotor A Thesis submitted to the Faculty of Graduate Studies of The University of Manitoba in partial fulfillment of the requirements of the degree of DOCTOR OF PHILOSOPHY Department of Computer Science University of Manitoba Winnipeg Copyright ⃝c 2010 by David Allenotor Abstract Many of the grid compute resources (CPU cycles, network bandwidths, computing power, processor times, and software) exist as non-storable commodities, which we call grid compute commodities (gcc) and are distributed geographically across organizations. These organizations have dissimilar resource compositions and usage policies, which makes pricing grid resources and guaranteeing their availability a challenge. Several initiatives (Globus, Legion, Nimrod/G) have developed various frameworks for grid resource management. However, there has been a very little effort in pricing the resources. In this thesis, we propose financial option based model for pricing grid resources by devising three research threads: pricing the gcc as a problem of real option, modeling gcc spot price using a discrete time approach, and addressing uncertainty constraints in the provision of Quality of Service (QoS) using fuzzy logic. We used GridSim, a simulation tool for resource usage in a Grid to experiment and test our model. To further consolidate our model and validate our results, we analyzed usage traces from six real grids from across the world for which we priced a set of resources. We designed a Price Variant Function (PVF) in our model, which is a fuzzy value and its application attracts more patronage to a grid that has more resources to offer and also redirect patronage from a grid that is very busy to another grid.
    [Show full text]
  • Local Volatility Modelling
    LOCAL VOLATILITY MODELLING Roel van der Kamp July 13, 2009 A DISSERTATION SUBMITTED FOR THE DEGREE OF Master of Science in Applied Mathematics (Financial Engineering) I have to understand the world, you see. - Richard Philips Feynman Foreword This report serves as a dissertation for the completion of the Master programme in Applied Math- ematics (Financial Engineering) from the University of Twente. The project was devised from the collaboration of the University of Twente with Saen Options BV (during the course of the project Saen Options BV was integrated into AllOptions BV) at whose facilities the project was performed over a period of six months. This research project could not have been performed without the help of others. Most notably I would like to extend my gratitude towards my supervisors: Michel Vellekoop of the University of Twente, Julien Gosme of AllOptions BV and Fran¸coisMyburg of AllOptions BV. They provided me with the theoretical and practical knowledge necessary to perform this research. Their constant guidance, involvement and availability were an essential part of this project. My thanks goes out to Irakli Khomasuridze, who worked beside me for six months on his own project for the same degree. The many discussions I had with him greatly facilitated my progress and made the whole experience much more enjoyable. Finally I would like to thank AllOptions and their staff for making use of their facilities, getting access to their data and assisting me with all practical issues. RvdK Abstract Many different models exist that describe the behaviour of stock prices and are used to value op- tions on such an underlying asset.
    [Show full text]
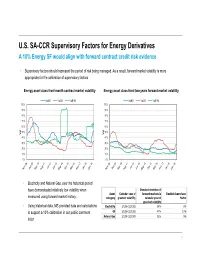
  • U.S. SA-CCR Supervisory Factors for Energy Derivatives a 10% Energy SF Would Align with Forward Contract Credit Risk Evidence
    U.S. SA-CCR Supervisory Factors for Energy Derivatives A 10% Energy SF would align with forward contract credit risk evidence • Supervisory factors should represent the period of risk being managed. As a result, forward market volatility is more appropriate for the calibration of supervisory factors Energy asset class front month contract market volatility Energy asset class front two years forward market volatility VolNG VolOil VolPJM VolNG VolOil VolPJM 100% 100% 90% 90% 80% 80% 70% 70% 60% 60% 50% 50% Vol Vol 40% 40% 30% 30% 20% 20% 10% 10% 0% 0% • Electricity and Natural Gas, over the historical period have demonstrated relatively low volatility when Standard deviation of Asset Calendar year of forward markets in Implied Supervisory measured using forward market history. category greatest volatility calendar year of Factor greatest volatility • Using historical data, MS provided data and calculations Electricity 1/1/08-12/31/08 24% 6% to support a 10% calibration in our public comment Oil 1/1/08-12/31/08 47% 13% Natural Gas 1/1/09-12/31/09 32% 9% letter 1 U.S. SA-CCR Supervisory Factors for Energy Derivatives A 10% Energy SF would align with credit risk in energy derivative transactions 1. Cal18 WTI Swap Pricing: Notional BBLs x Cal18 Prices 2. Cal18 WTI MTM vs SA-CCR vs Mean Positive Exposure 150 90 Oil 1 0 /12 450 1 /10 80 1 1 100 /11 /8 1 1 350 /9 /6 70 1 1 /7 /4 1 1 50 /5 /2 60 250 1 1 /3 50 - $MM 150 $MM 40 $/BBL 50 (50) 30 20 -50 (100) 10 -150 (150) 0 Cal18 MTM SA-CCR RWA Exposure at 40% SF Cal18 MTM ($MM) Notional Quantity (BBLs) * SA-CCR RWA Exposure at 10% SF Max Mean Positive Exposure Cal18 Price ($/BBL) 1/# Spot Contribution to MTM • Energy derivative counterparty credit risk exposures decline, • A 10% Supervisory Factor correctly aligns SA-CCR month by month, as the transaction nears maturity since the credit risk measurements with other reliable counterparty remaining total notional quantity declines credit risk measures (i.e.
    [Show full text]
  • Pricing Options Using Trinomial Trees
    Pricing Options Using Trinomial Trees Paul Clifford Yan Wang Oleg Zaboronski 30.12.2009 1 Introduction One of the first computational models used in the financial mathematics community was the binomial tree model. This model was popular for some time but in the last 15 years has become significantly outdated and is of little practical use. However it is still one of the first models students traditionally were taught. A more advanced model used for the project this semester, is the trinomial tree model. This improves upon the binomial model by allowing a stock price to move up, down or stay the same with certain probabilities, as shown in the diagram below. 2 Project description. The aim of the project is to apply the trinomial tree to the following problems: ² Pricing various European and American options ² Pricing barrier options ² Calculating the greeks More precisely, the students are asked to do the following: 1. Study the trinomial tree and its parameters, pu; pd; pm; u; d 2. Study the method to build the trinomial tree of share prices 3. Study the backward induction algorithms for option pricing on trees 4. Price various options such as European, American and barrier 1 5. Calculate the greeks using the tree Each of these topics will be explained very clearly in the following sections. Students are encouraged to ask questions during the lab sessions about certain terminology that they do not understand such as barrier options, hedging greeks and things of this nature. Answers to questions listed below should contain analysis of numerical results produced by the simulation.
    [Show full text]
  • On Trinomial Trees for One-Factor Short Rate Models∗
    On Trinomial Trees for One-Factor Short Rate Models∗ Markus Leippoldy Swiss Banking Institute, University of Zurich Zvi Wienerz School of Business Administration, Hebrew University of Jerusalem April 3, 2003 ∗Markus Leippold acknowledges the financial support of the Swiss National Science Foundation (NCCR FINRISK). Zvi Wiener acknowledges the financial support of the Krueger and Rosenberg funds at the He- brew University of Jerusalem. We welcome comments, including references to related papers we inadvertently overlooked. yCorrespondence Information: University of Zurich, ISB, Plattenstr. 14, 8032 Zurich, Switzerland; tel: +41 1-634-2951; fax: +41 1-634-4903; [email protected]. zCorrespondence Information: Hebrew University of Jerusalem, Mount Scopus, Jerusalem, 91905, Israel; tel: +972-2-588-3049; fax: +972-2-588-1341; [email protected]. On Trinomial Trees for One-Factor Short Rate Models ABSTRACT In this article we discuss the implementation of general one-factor short rate models with a trinomial tree. Taking the Hull-White model as a starting point, our contribution is threefold. First, we show how trees can be spanned using a set of general branching processes. Secondly, we improve Hull-White's procedure to calibrate the tree to bond prices by a much more efficient approach. This approach is applicable to a wide range of term structure models. Finally, we show how the tree can be adjusted to the volatility structure. The proposed approach leads to an efficient and flexible construction method for trinomial trees, which can be easily implemented and calibrated to both prices and volatilities. JEL Classification Codes: G13, C6. Key Words: Short Rate Models, Trinomial Trees, Forward Measure.
    [Show full text]
  • Derivatives and Risk Management in the Petroleum, Natural Gas, and Electricity Industries
    SR/SMG/2002-01 Derivatives and Risk Management in the Petroleum, Natural Gas, and Electricity Industries October 2002 Energy Information Administration U.S. Department of Energy Washington, DC 20585 This report was prepared by the Energy Information Administration, the independent statistical and analytical agency within the U.S. Department of Energy. The information contained herein should be attributed to the Energy Information Administration and should not be construed as advocating or reflecting any policy position of the Department of Energy or any other organization. Service Reports are prepared by the Energy Information Administration upon special request and are based on assumptions specified by the requester. Contacts This report was prepared by the staff of the Energy The Energy Information Administration would like to Information Administration and Gregory Kuserk of the acknowledge the indispensible help of the Commodity Commodity Futures Trading Commission. General Futures Trading Commission in the research and writ- questions regarding the report may be directed to the ing of this report. EIA’s special expertise is in energy, not project leader, Douglas R. Hale. Specific questions financial markets. The Commission assigned one of its should be directed to the following analysts: senior economists, Gregory Kuserk, to this project. He Summary, Chapters 1, 3, not only wrote sections of the report and provided data, and 5 (Prices and Electricity) he also provided the invaluable professional judgment Douglas R. Hale and perspective that can only be gained from long expe- (202/287-1723, [email protected]). rience. The EIA staff appreciated his exceptional pro- ductivity, flexibility, and good humor.
    [Show full text]
  • Volatility Curves of Incomplete Markets
    Master's thesis Volatility Curves of Incomplete Markets The Trinomial Option Pricing Model KATERYNA CHECHELNYTSKA Department of Mathematical Sciences Chalmers University of Technology University of Gothenburg Gothenburg, Sweden 2019 Thesis for the Degree of Master Science Volatility Curves of Incomplete Markets The Trinomial Option Pricing Model KATERYNA CHECHELNYTSKA Department of Mathematical Sciences Chalmers University of Technology University of Gothenburg SE - 412 96 Gothenburg, Sweden Gothenburg, Sweden 2019 Volatility Curves of Incomplete Markets The Trinomial Asset Pricing Model KATERYNA CHECHELNYTSKA © KATERYNA CHECHELNYTSKA, 2019. Supervisor: Docent Simone Calogero, Department of Mathematical Sciences Examiner: Docent Patrik Albin, Department of Mathematical Sciences Master's Thesis 2019 Department of Mathematical Sciences Chalmers University of Technology and University of Gothenburg SE-412 96 Gothenburg Telephone +46 31 772 1000 Typeset in LATEX Printed by Chalmers Reproservice Gothenburg, Sweden 2019 4 Volatility Curves of Incomplete Markets The Trinomial Option Pricing Model KATERYNA CHECHELNYTSKA Department of Mathematical Sciences Chalmers University of Technology and University of Gothenburg Abstract The graph of the implied volatility of call options as a function of the strike price is called volatility curve. If the options market were perfectly described by the Black-Scholes model, the implied volatility would be independent of the strike price and thus the volatility curve would be a flat horizontal line. However the volatility curve of real markets is often found to have recurrent convex shapes called volatility smile and volatility skew. The common approach to explain this phenomena is by assuming that the volatility of the underlying stock is a stochastic process (while in Black-Scholes it is assumed to be a deterministic constant).
    [Show full text]
  • Robust Option Pricing: the Uncertain Volatility Model
    Imperial College London Department of Mathematics Robust option pricing: the uncertain volatility model Supervisor: Dr. Pietro SIORPAES Author: Hicham EL JERRARI (CID: 01792391) A thesis submitted for the degree of MSc in Mathematics and Finance, 2019-2020 El Jerrari Robust option pricing Declaration The work contained in this thesis is my own work unless otherwise stated. Signature and date: 06/09/2020 Hicham EL JERRARI 1 El Jerrari Robust option pricing Acknowledgements I would like to thank my supervisor: Dr. Pietro SIORPAES for giving me the opportunity to work on this exciting subject. I am very grateful to him for his help throughout my project. Thanks to his advice, his supervision, as well as the discussions I had with him, this experience was very enriching for me. I would also like to thank Imperial College and more particularly the \Msc Mathemat- ics and Finance" for this year rich in learning, for their support and their dedication especially in this particular year of pandemic. On a personal level, I want to thank my parents for giving me the opportunity to study this master's year at Imperial College and to be present and support me throughout my studies. I also thank my brother and my two sisters for their encouragement. Last but not least, I dedicate this work to my grandmother for her moral support and a tribute to my late grandfather. 2 El Jerrari Robust option pricing Abstract This study presents the uncertain volatility model (UVM) which proposes a new approach for the pricing and hedging of derivatives by considering a band of spot's volatility as input.
    [Show full text]
  • The Hull-White Model • Hull and White (1987) Postulate the Following Model, Ds √ = R Dt + V Dw , S 1 Dv = Μvv Dt + Bv Dw2
    The Hull-White Model • Hull and White (1987) postulate the following model, dS p = r dt + V dW ; S 1 dV = µvV dt + bV dW2: • Above, V is the instantaneous variance. • They assume µv depends on V and t (but not S). ⃝c 2014 Prof. Yuh-Dauh Lyuu, National Taiwan University Page 599 The SABR Model • Hagan, Kumar, Lesniewski, and Woodward (2002) postulate the following model, dS = r dt + SθV dW ; S 1 dV = bV dW2; for 0 ≤ θ ≤ 1. • A nice feature of this model is that the implied volatility surface has a compact approximate closed form. ⃝c 2014 Prof. Yuh-Dauh Lyuu, National Taiwan University Page 600 The Hilliard-Schwartz Model • Hilliard and Schwartz (1996) postulate the following general model, dS = r dt + f(S)V a dW ; S 1 dV = µ(V ) dt + bV dW2; for some well-behaved function f(S) and constant a. ⃝c 2014 Prof. Yuh-Dauh Lyuu, National Taiwan University Page 601 The Blacher Model • Blacher (2002) postulates the following model, dS [ ] = r dt + σ 1 + α(S − S ) + β(S − S )2 dW ; S 0 0 1 dσ = κ(θ − σ) dt + ϵσ dW2: • So the volatility σ follows a mean-reverting process to level θ. ⃝c 2014 Prof. Yuh-Dauh Lyuu, National Taiwan University Page 602 Heston's Stochastic-Volatility Model • Heston (1993) assumes the stock price follows dS p = (µ − q) dt + V dW1; (64) S p dV = κ(θ − V ) dt + σ V dW2: (65) { V is the instantaneous variance, which follows a square-root process. { dW1 and dW2 have correlation ρ.
    [Show full text]
  • Long-Term Swings and Seasonality in Energy Markets Working Paper Nº 1929
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by EPrints Complutense Long-term swings and seasonality in energy markets Instituto Manuel Moreno Complutense Department of Economic Analysis and Finance, University of Castilla-La Mancha, Toledo, Spain de Análisis Económico Alfonso Novales Instituto Complutense de Análisis Económico (ICAE), and Department of Economic Analysis, Facultad de Ciencias Económicas y Empresariales, Universidad Complutense, Madrid, Spain Federico Platania Léonard de Vinci Pôle Universitaire, Paris La Défense, France Abstract This paper introduces a two-factor continuous-time model for commodity pricing under the assumption that prices revert to a stochastic mean level, which shows smooth, periodic fluctuations over long periods of time. We represent the mean reversion price by a Fourier series with a stochastic component. We also consider a seasonal component in the price level, an essential characteristic of many commodity prices, which we represent again by a Fourier series. We obtain analytical pricing expressions for futures contracts. Using futures price data on Natural Gas, we provide evidence on the presence of long-term fluctuations and show how to estimate the long-term component simultaneously with a seasonal component using the Kalman filter. We analyse the in-sample and out-of-sample empirical performance of our pricing model with and without a seasonal component and compare it with the Schwartz and Smith (2000) model. Our findings show the in-sample and out-of-sample superiority of our model with seasonal fluctuations, thereby providing a simple and powerful tool for portfolio management, risk management, and derivative pricing.
    [Show full text]
  • Local and Stochastic Volatility Models: an Investigation Into the Pricing of Exotic Equity Options
    Local and Stochastic Volatility Models: An Investigation into the Pricing of Exotic Equity Options A dissertation submitted to the Faculty of Science, University of the Witwatersrand, Johannesburg, South Africa, in ful¯llment of the requirements of the degree of Master of Science. Abstract The assumption of constant volatility as an input parameter into the Black-Scholes option pricing formula is deemed primitive and highly erroneous when one considers the terminal distribution of the log-returns of the underlying process. To account for the `fat tails' of the distribution, we consider both local and stochastic volatility option pricing models. Each class of models, the former being a special case of the latter, gives rise to a parametrization of the skew, which may or may not reflect the correct dynamics of the skew. We investigate a select few from each class and derive the results presented in the corresponding papers. We select one from each class, namely the implied trinomial tree (Derman, Kani & Chriss 1996) and the SABR model (Hagan, Kumar, Lesniewski & Woodward 2002), and calibrate to the implied skew for SAFEX futures. We also obtain prices for both vanilla and exotic equity index options and compare the two approaches. Lisa Majmin September 29, 2005 I declare that this is my own, unaided work. It is being submitted for the Degree of Master of Science to the University of the Witwatersrand, Johannesburg. It has not been submitted before for any degree or examination to any other University. (Signature) (Date) I would like to thank my supervisor, mentor and friend Dr Graeme West for his guidance, dedication and his persistent e®ort.
    [Show full text]