DOCSLIB.ORG

The Effectiveness of Differential Moment Strategies in Anchorage Control During Space Closure" (2000)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Effectiveness of Differential Moment Strategies in Anchorage Control During Space Closure University of Connecticut OpenCommons@UConn SoDM Masters Theses School of Dental Medicine June 2000 The ffecE tiveness of Differential Moment Strategies in Anchorage Control During Space Closure Derek N. Priebe Follow this and additional works at: https://opencommons.uconn.edu/sodm_masters Recommended Citation Priebe, Derek N., "The Effectiveness of Differential Moment Strategies in Anchorage Control During Space Closure" (2000). SoDM Masters Theses. 107. https://opencommons.uconn.edu/sodm_masters/107 THE EFFECTIVENESS OF DIFFERENTIAL MOMENT STRATEGIES IN ANCHORAGE CONTROL DURING SPACE CLOSURE Derek N. Priebe B.A., Arizona State University, 1988 D.D.S., University of the Pacific School of Dentistry, 1997 A Thesis Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Dental Science at the University of Connecticut 2000 APPROVAL PAGE Master of Dental Science Thesis THE EFFECTIVENESS OF DIFFERENTIAL MOMENT STRATEGIES IN ANCHORAGE CONTROL DURING SPACE CLOSURE Presented by Derek N. Priebe, D.D.S. Major Advisor --....-~L.___./r~ Andfel;J. Kuhlberg b Associa~Ad~sor~~~~~~~~~~~~~~~~~~~~~~~~~ Ravindra Nanda ~/_ t.~ Associate Advisor_~~~~_=~Q_-~_-......-_;.~(~~~~~~~~_~~~_~_... I C Eung-Kwon Pae University of Connecticut 2000 ii PREFACE The field of biomechanics has been mindfully applied to the principles of orthodontic appliance design. The assumption, however, that the force system is the determinant factor in treatn1ent response has not been vigorously tested. The relationship between the appliance-delivered stimulus and the biological response, therefore, warrants clinical docllmentation. Analagous to the dose-response model of contemporary medicine, a "stimulus-response" model is useful in determining the effectiveness of the care promoted by our specialty. Because the act of orthodontic space closure typically involves substantial tooth displacement, it invites study of the effects of force system delivery and treatment response. From a clinical perspective, the delivery of appropriate force systems during space closure aims at efficient tooth movements and maintenance of anchorage. From the perspective of force system delivery approaches, the evaluation of pre-determined and preferential tooth movements during space closure will aid in testing a stimulus-response model of orthodontic treatment. Specifically, differential moment strategies for anchorage control hinge on the assumption of a force system stimulus-response model. A clinical study using qualitative force systems during extraction space closure will serve as an ideal arena for evaluating whether biomechanics "works the way it's supposed to." A non-randomized clinical trial was conducted to investigate a force system stimulus - tooth movement response model. Sixteen patients undergoing three months of en masse space closure with concomitant posterior anchorage served as subjects. T-loop retraction springs delivering, at the least, qualitative force systems were used as the iii stimulus. A carefully designed cephalometric approach was used to assess the response. The findings suggest that the force system does in fact predict the dental response. Preferential retraction of six maxillary anterior teeth occurred with little displacement of two maxillary molars serving as anchorage units (p < 0.0001). The physics of the force system are therefore predictive of the resultant dental displacements despite a biologic environment. While the average responses prompt a rejection of the null hypothesis, a substantial amOllnt of intra- and inter-subject variability was documented. Nevertheless, the significance of this investigation is the documentation of a short-term response to a qualitative stimulus without confounding effects of continued treatment. The docllmentation of responses occurring as a result of relatively discrete stimuli enhance the orthodontists' ability to make reasonably predictable in-course corrections. iv ACKNOWLEDGEMENTS The act of research and thesis preparation is analagous to many of life's pursuits; one's endeavors are often characterized by the ebb and flow of progress. Indeed, net success is dependent on careful planning, problem solving, and resolve. Any achievement, however, is impossible without the unselfish support of one's peers, mentors and family ("it takes a village..." so to speak). The production of this investigation is a clear example of the redoubt of collaboration and is ultimately much less a product of the principal author as it is several individuals. DR. ANDREW J. KUHLBERG The execution of this manuscript would have been absolutely impossible if it were not for the lucid support and tutelage of Dr. Andrew J. Kuhlberg. Featured prominently in several contemporary thesis acknowledgements, Andy is the heart and soul of clinical orthodontic research at the University of Connecticut. He demonstrates vision and sagacity well beyond his years. In short, he's a one man "think tank." Without Andy's presence in the department, my education would be a fractional shadow of what it has become. Most importantly, Andy has become my friend with whom I hope to maintain close collaboration over the years to come. DR. RAVINDRA NANDA Just slightly over three years ago, I received a personal phone call from a department chair offering an interview for a spot in the program. That, in itself, nearly concluded a difficult decision. Since then, Dr. Nanda has been like a father to me with a keen perception of life. Dr. Nanda has been a shining light and inspiration to dozens of v orthodontic residents. lowe my current and future career to Dr. Nanda for "taking a chance on me." DR. EUNG-KWON PAE Dr. Pae has always taken the time out of an impossible schedule to listen to the myriad of problems arising during the preparation of this project. His selfless suggestions have been instrumental in improving the research design and statistical methods of this project. DR. STEPHEN GODWIN G-ratitude goes to Dr. Godwin for keeping this project moving along in a timely manner. He's offered both positive support and constructive suggestions. RESIDENTS The difficult task of patient selection was supported admirably by the exceptional residents of the Orthodontics Class of 2001. Notably, this project would have fallen short without the alert help of Drs. Danielle Battisti, Jeff Blasius, and Zack Faber. I also owe thanks to Dr. Sunil "Hey Buddy" Wadhwa for acting as my counselor and friend over the three years of my residency. Thank-you, I'm indebted to you all! MY FAMILY Finally, lowe all my success to the love of my wife Ingvild, my two wonderful children, Annika and Anders, and my parents, Mary and Phil Priebe. My wife especially deserves a medal for being a citadel of support as I've hauled her from one corner of North America to another. Ingvild and Mom and Dad, you've stuck by me over the years and have selflessly offered your love and support at great sacrifice. Annika and Anders, you are my precious little gems! I love you all, and to you I dedicate this work. VI TABLE OF CONTENTS Chapter I INTRODUCTION and REVIEW OF LITERATURE 1 Dental Anchorage Control dllring Space Closure 2 Force Magnitudes and Optimum Orthodontic Forces 9 Force Systems and Biomechanics in Orthodontics 21 Moment-to-Force Ratios and Centers of Rotation 21 Differential Moment Strategies in Anchorage Control 26 Chapter II OBJECTIVES and RATIONALE 32 Hypotheses 33 Chapter III EXPERIMENTAL METHOD 34 Sample 34 Materials and Method 35 T-Loop Force System 36 Recording Technique 39 Superimposition Method 40 Measurement Technique 41 Data Handling 42 Measurenlent Error Method 42 vii Chapter IV RESULTS 43 Observation Period 43 Measllrement Error 43 Total Space Closure 43 Anchorage Maintenance and Anterior Retraction 44 Vertical Response 45 Angular Response 45 Chapter V DISCUSSION 47 Anteroposterior and Angular Responses 48 Vertical Responses 49 Observed Variation 51 Variation as the Fllnction of the Stimulus 52 Variation as the Function of Biologic Factors 53 Variation as a Function of the Measurement Technique 54 Chapter VI SUMMARY 56 CONCLUSIONS 57 BIBLIOGRAPHY 77 viii LIST of TABLES Table I Force System Produced by Asymmetrically Placed T-Loops 74 Table II Error Standard Deviation of Repeat Measurements 75 Table III Variable Means, Standard Deviations, and Ranges 76 IX LIST OF FIGURES Figure 1: Graphic ofGeometric Description ofDifferential Tooth Movement 58 Figure 2: Graphic ofBiologic Description ofDifferential Tooth Movement 59 Figure 3: Differential Moment Force System 60 Figure 4: Pre-fabricated .017" by .025" f3-titanium closing loop arch wire 61 Figure 5: Schematic ofloop position with 2.0 mm off-set 62 Figure 6: Intra-oral photo ofactivated closing loop with 2.0 mm off-set 63 Figure 7: Cephalometric radiograph with TPLDs 64 Figure 8: Tracing superimposition ofT] and T2 films with TPLD images representing dental changes 65 Figure 9: Distribution ofobservation periods 66 Figure 10: Distribution oftotal space closure 67 Figure 11: Distribution ofnormalized anteroposterior tooth movements - Anchorage Loss 68 Figure 12: Distribution ofnormalized anteroposterior tooth movements - canine retraction versus anchorage 69 x Figure 13: Distribution ofmolar vertical response 70 Figure 14: Distribution ofcanine vertical response 71 Figure 15: Distribution ofcanine and molar angular response 72 Figure 16: Graphic illustration ofmean molar and canine anteroposterior, Vertical and angular responses 73 Xl Ie Introduction and Review of Literature The field of biomechanics has been mindfully
Load more

Recommended publications
  • V September 2006
    CORRELATING POSITION OF HYOID BONE AND MANDIBLE TO THIRD CERVICAL VERTEBRA IN PATIENTS WITH CLASS I, CLASS II AND CLASS III SKELETAL MALOCCLUSION – A CEPHALOMETRIC STUDY Dissertation Submitted to THE TAMIL NADU DR.M.G.R. MEDICAL UNIVERSITY Towards the partial fulfillment for the degree of MASTER OF DENTAL SURGERY BRANCH – V ORTHODONTICS SEPTEMBER 2006 Certificate This is to certify that Dr. VIJJAYKANTH Post Graduate Student (2003-2006) in the Department of Orthodontics, Tamilnadu Government Dental College & Hospital, Chennai has done this dissertation titled “CORRELATING POSITION OF HYOID BONE AND MANDIBLE TO THIRD CERVICAL VERTEBRA IN PATIENTS WITH CLASS I, CLASS II AND CLASS III SKELETAL MALOCCLUSION – A CEPHALOMETRIC STUDY” under our guidance and supervision in partial fulfillment of the regulations laid down by the Tamilnadu Dr.M.G.R. Medical University, Chennai for M.D.S., Branch – V Orthodontics, Degree Examination. Dr.L.Muthusamy, M.D.S., Dr.W.S.Manjula, M.D.S., Professor and Head, Additional Professor, Department of Orthodontics Department of Orthodontics Tamilnadu Govt. Dental College and Hospital, Tamilnadu Govt. Dental College and Hospital, Chennai-600 003. Chennai-600 003. Dr.C. Kumaravelu, M.D.S., Principal Tamilnadu Govt. Dental College and Hospital, Chennai-600 003. C O N T E N T S PAGE NO. 1 INTRODUCTION 01 2 AIMS AND OBJECTIVES 04 3 REVIEW OF LITERATURE 05 4 MATERIALS AND METHODS 24 5 RESULTS 29 6 DISCUSSION 41 7 SUMMARY AND CONCLUSION 50 8 BIBLIOGRAPHY 52 LIST OF BAR DIAGRAMS Bar Diagram Bar Diagram Title No 1. Cephalometric mean and standard deviation for each group Cephalometric mean values for male and female subjects for each 2.
    [Show full text]
  • The Effectiveness of Tipback Mechanics for Correction of Class II Malocclusion" (2014)
    University of Connecticut OpenCommons@UConn Master's Theses University of Connecticut Graduate School 7-3-2014 The ffecE tiveness of Tipback Mechanics for Correction of Class II Malocclusion Nandakumar Janakiraman University of Connecticut School of Medicine and Dentistry, [email protected] Recommended Citation Janakiraman, Nandakumar, "The Effectiveness of Tipback Mechanics for Correction of Class II Malocclusion" (2014). Master's Theses. 632. https://opencommons.uconn.edu/gs_theses/632 This work is brought to you for free and open access by the University of Connecticut Graduate School at OpenCommons@UConn. It has been accepted for inclusion in Master's Theses by an authorized administrator of OpenCommons@UConn. For more information, please contact [email protected]. The Effectiveness of Tipback Mechanics for Correction of Class II Malocclusion. Nandakumar Janakiraman B.D.S. Government Dental College, Bangalore University, 1997. M.D.S. Government Dental College, NTR University, 2002. A Thesis Submitted in Partial Fulfillment of the Requirements for the Degree of Masters of Dental Science at the University of Connecticut 2014 i APPROVAL PAGE Master of Dental Science Thesis The Effectiveness of Tipback Mechanics for Correction of Class II Malocclusion Presented by Nandakumar Janakiraman, BDS, MDS Major Advisor________________________________________________ Flavio A. Uribe DDS, MDentSc Associate Advisor_____________________________________________ Ravindra Nanda BDS, MDS, PhD Associate Advisor_____________________________________________ David Shafer DMD University of Connecticut 2014 ii Acknowledgments I want to thank my parents, my wife and kids for all the sacrifices they make to make my dream come true. I want to thank Dr. Nanda, Dr. Uribe and School of Dental Medicine, University of Connecticut, for their support, encouragement, constant guidance and making my dream of becoming an Orthodontist in US.
    [Show full text]
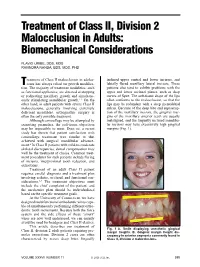
  • Treatment of Class II, Division 2 Malocclusion in Adults: Biomechanical Considerations
    Treatment of Class II, Division 2 Malocclusion in Adults: Biomechanical Considerations FLAVIO URIBE, DDS, MDS RAVINDRA NANDA, BDS, MDS, PHD reatment of Class II malocclusion in adoles- inclined upper central and lower incisors, and Tcents has always relied on growth modifica- labially flared maxillary lateral incisors. These tion. The majority of treatment modalities, such patients also tend to exhibit problems with the as functional appliances, are directed at stopping upper and lower occlusal planes, such as deep or redirecting maxillary growth and simultane- curves of Spee. The soft-tissue drape of the lips ously stimulating mandibular growth.1-3 On the often conforms to the malocclusion, so that the other hand, in adult patients with severe Class II lips may be redundant with a deep mentolabial malocclusions, generally involving extremely sulcus. Because of the deep bite and supraerup- deficient mandibles, orthognathic surgery is tion of the maxillary incisors, the gingival mar- often the only possible treatment. gins of the maxillary anterior teeth are usually Although camouflage may be attempted by malaligned, and the lingually inclined mandibu- extracting premolars, the soft-tissue objectives lar incisors may have excessively high gingival may be impossible to meet. Even so, a recent margins (Fig. 1). study has shown that patient satisfaction with camouflage treatment was similar to that achieved with surgical mandibular advance- ment.4 In Class II patients with mild-to-moderate skeletal discrepancies, dental compensation may well be the treatment of choice. Common treat- ment procedures for such patients include flaring of incisors, interproximal tooth reduction, and extractions. Treatment of an adult Class II patient requires careful diagnosis and a treatment plan involving esthetic, occlusal, and functional con- siderations.5-7 The treatment objectives must include the chief complaint of the patient, and A the mechanics plan should be individualized based on the specific treatment goals.
    [Show full text]
  • Angle Society to Celebrate Diamond Anniversary August 21–25, 2005
    Published by the Edward H. Angle Society of Orthodontists, Inc., The E.H. Angle Education and Research Foundation, Inc. Volume 15, No. 1 ISSN 1098-1624 July 2005 AMESSAGE FROM THE PRESIDENT… Angle Society to celebrate Diamond Anniversary August 21–25, 2005 Happy 75th anniversary, Angle Society! Angle members and historians spent more than Happy 150th birthday, Dr. Angle! one year in preparation for this new documen- tary to be released at this meeting. The 36th Biennial Meeting is fast approaching and Evening entertainment on Monday will include plans are finalizing for a spectacular 75th jubilee a spectacular sunset dinner cruise on the Tahoe meeting on the northern shore of beautiful Lake Queen, a throwback paddlewheel ship complete Tahoe at Incline Village, Nevada. The Hyatt with live band. Watching the sunset over the Regency Lake Tahoe Resort, Spa and Casino is Sierras while cruising on this alpine jewel is a ready and five-star worthy of our historic meeting. continued on page 3 We have solicited component speakers and have included several special presentations for an enhanced scientific session experience. Many members from the Angle Society of Europe will attend and some will participate in our program as guests of the society on this historic occasion. To mention just a few speak- ers, get ready to learn from Drs. Don Joondeph, Vince Kokich, David Hatcher, Rick McLaughlin, Dave Turpin, Roger Boero and Hans Pancherz from Europe. Dr. Art Dugoni will present the keynote Angle Memorial Lecture. Registration information has already been mailed and response has been brisk. Registering now before June 21 will assure your acceptance and lower your costs.
    [Show full text]
  • Volume 17, Issue 1
    Published by the Edward H. Angle Society of Orthodontists, Inc., The E.H. Angle Education and Research Foundation, Inc. Volume 17, No. 1 ISSN 1098-1624 July 2007 A MESSAGE FROM THE PRESIDENT… Allen Moffitt: “ABO resident clinical outcomes study and more…” Don Burden: “Long-term outcomes following treatment of th As the 37 Biennial of the Edward class II, division 1 malocclusion using fixed appliances.” H. Angle Society of Orthodontists enters the final months of prepara- Dianne Rekow: “New advances in tissue engineering for tion, I am happy to report that all craniofacial repair.” of the elements of an “historic and Heon-Jae Cho: “The long-term stability of mandibular set- memorable” Biennial have been back surgery.” put in place. Maryse Aubert: “New perspective on early treatment: ■ Outstanding location—Chateau Comparison of data from treatment started in mixed dentition Frontenac, Quebec City and permanent dentition.” ■ Perfect timing (September 16- Doug Knight: “What I learned through prospective treatment 20th)—Fall colors and cool evening of my Angle cases. walks in “Old Quebec City” ■ Social activities—opening cock- Rob Elliott: “The partnership of orthodontic and restorative Dr. David R. Musich tail welcome; boat trip up St. therapies- key elements of communication.” President Lawrence river with dinner and Alice Shen: “Maxillary impacted cuspids: can the problems dancing; and spectacular gala ban- be prevented?” quet in Frontenac’s exquisite ballroom. There will be a number of optional events: golf, cooking classes, a day trip to Bay St. Paul Jim Zahrowskie: “Bisphosphonate and orthodontics.” (Charlevoix Region), and a bus tour of Quebec City. Jimmy C.
    [Show full text]
  • Integration of 3-Dimensional Surgical and Orthodontic Technologies with Orthognathic “Surgery-first” Approach in the Management of Unilateral Condylar Hyperplasia
    CLINICIAN'S CORNER Integration of 3-dimensional surgical and orthodontic technologies with orthognathic “surgery-first” approach in the management of unilateral condylar hyperplasia Nandakumar Janakiraman,a Mark Feinberg,b Meenakshi Vishwanath,c Yasas Shri Nalaka Jayaratne,c Derek M. Steinbacher,d Ravindra Nanda,e and Flavio Uribef Farmington, Shelton, and New Haven, Conn Recent innovations in technology and techniques in both surgical and orthodontic fields can be integrated, espe- cially when treating subjects with facial asymmetry. In this article, we present a treatment method consisting of 3- dimensional computer-aided surgical and orthodontic planning, which was implemented with the orthognathic surgery-first approach. Virtual surgical planning, fabrication of surgical splints using the computer-aided design/computer-aided manufacturing technique, and prediction of final orthodontic occlusion using virtual plan- ning with robotically assisted customized archwires were integrated for this patient. Excellent esthetic and occlusal outcomes were obtained in a short period of 5.5 months. (Am J Orthod Dentofacial Orthop 2015;148:1054-66) he advent of the digital era has enabled clinicians dental history, especially when treating complex maloc- Tto use the best available data for evidence-based clusions with orthognathic surgery.1 Traditionally, diagnosis, treatment planning, and execution of 2-dimensional (2D) imaging has been the standard for treatment. For accurate diagnosis, obtaining precise representing the 3-dimensional (3D) craniofacial
    [Show full text]
  • Kurs Melbourne Nanda.Indd
    MELBOURNE HOW TO REGISTER INDUSTRY SPONSORS November 24. | 25. 2017 Name: Address: OURSES COURSES COURSES C Primary Sponsors URSESInvitation COURSES COURSES CO Email RSES COURSES COURSES COU PAYMENT: University of Melbourne Orthodontic SES BiologyCOURSES + Biomechanics COURSES COUR Alumni / ASO / NZAO member Day 1 [lectures] $580 Day 2 [hands-on] $380 ES COURSESthe heart of Orthodontics COURSES COURS Day 1 + Day 2 $960 S COURSES COURSES COURSE Non Member Day 1 [lectures] $680 Day 2 [hands-on] $480 Day 1 + Day 2 $1160 COURSES COURSES COURSES Retired member Day 1 $300 OURSES COURSES COURSES C Postgraduate Orthodontic Student URSES COURSES COURSES CO Day 1 $0 Supporting Sponsors RSES COURSES COURSES COU ASOVB ANNUAL DINNER [limit 42 pax] Featuring Partners & guests are welcome SES COURSES COURSESDr. Ravi Nanda COUR $150 pp No. Attending:___ ES COURSES COURSES COURS RSVP: ASO Victorian Branch + Electronic 1/Email your registration information (Name, S COURSESUniversity of Melbourne COURSES Orthodontic COURSE Alumni Address, Payment Details) to: [email protected] 2/Pay via electronic fund transfer to: COURSES COURSES COURSES Account Name: Australian Society of Orthodontists Victoria Branch BSB: 033-157 OURSES COURSES COURSES C Account Number:227861 *** Please include your name in the funds transaction*** URSES COURSES COURSES CO Post Print and fill in this registration form, and post to: RSES COURSES COURSES COU Dr. Adam Rose ASOVB Treasurer SES COURSES COURSES COUR 260 Jasper Road McKinnon, 3204 ES COURSES COURSES COURS *** Please make cheque payable to Australian Society of Orthodontists Victoria Branch*** S COURSES COURSES COURSE est. 1991 Enquiries: Dr Albert Wong ([email protected]) or COURSES COURSES COURSES Dr Adam Rose ([email protected]) OURSES COURSES COURSES C Friday 24.
    [Show full text]
  • Level 1: Treatment of Simple to Moderate Malocclusions
    LEVEL 1: TREATMENT OF SIMPLE TO MODERATE MALOCCLUSIONS COURSE OUTLINE COURSE NAME “Orthodontic Management of Simple to Moderate Malocclusions: an Online and Onsite Course for Dentists” This course is designed to improve the knowledge and ability of dentists from emerging countries to diagnose, select, and treat patients with moderate malocclusions. It is an 18-month course that uses blended learning to provide general dentists with an opportunity to learn how to manage orthodontic treatment of patients with moderately complex malocclusions at an internationally acceptable level. The online modules allow students to learn and study at home or work while onsite sessions (in dedicated cities) and online supervision allow students to learn and practice patient skills under the supervision of orthodontists recognized by the World Federation of Orthodontists (WFO). This course does not replace post-graduate specialist programs, but it is a step forward in teaching international level orthodontic care. www.discoverortho.com Page 1 GOALS This course is designed to improve the knowledge and ability of dentists to diagnose, select, and treat patients with moderate malocclusions. At the end of the course, participants are expected to be able to recognize, diagnose, select, and manage the treatment of patients with moderate malocclusions. Participating dentists will also learn to recognize and to refer more severe or complex cases to specialists or other dentists better- trained in orthodontics. PROGRAM DIRECTOR Jean-Marc Retrouvey, DMD, MSc, FRCD Department Chair & Professor, Orthodontics & Dentofacial Orthopedics, University of Missouri- Kansas City, USA Program Director and President, IFDE Email: [email protected] CLINICAL DIRECTOR Neil Kay, BSc, BDS, MS Orthodontist Clinical Director, IFDE Health Volunteers Overseas (HVO) Orthodontic Representative for Vietnam LOCAL FACULTY www.discoverortho.com Page 2 REFERENCE TEXTS, REFERENCES, AND MANUALS Orthodontic Diagnosis – Dr.
    [Show full text]
  • Jim Hugg Receives Shepard Award MSO’S Board of Directors Voted Unanimously to Nent, Constituent and National AAO Levels Serving on a Present the 2002 Earl E
    MSO NEWSLETTER A Publication of the Midwestern Society of Orthodontists Winter 2003 Jim Hugg Receives Shepard Award MSO’s Board of Directors voted unanimously to nent, constituent and national AAO levels serving on a present the 2002 Earl E. Shepard Distinguished Service variety of committees and taskforces, including as a delegate Award to Dr. James R. Hugg, Burlington, Iowa, for his representing the MSO to the AAO House of Delegates. exemplary contributions to the art and science of orthodon- Jim’s advance research, statistics, typed background support tics. This award recognizes a member of the MSO who documents and “big-picture, forward-thinking” insight have exemplifies the ideals of the orthodontic profession, been invaluable in moving the specialty forward. community and family. In addition, Jim has served as a delegate to the Jim was born and raised in Burlington where his American Dental Association, and he also received the professional career began after he received his dental degree Presidential Award for Service to the Iowa Dental Associa- from the University of Iowa in 1953. Fifteen years later he tion in 1990. He is a Fellow of the American College of received a Masters in Orthodontics from the University of Dentists, the International College of Dentists and the Pierre Iowa. He practiced with Dr. Phil Doster in Burlington from Fauchard Academy. 1968 to 1970 and then maintained his own solo practice Jim currently is working on implementing a until his daughter-in-law, Dr. Teresa Salino-Hugg, joined comprehensive continuing education program for ortho- him in 1987. dontic assistants utilizing the Iowa Communication Network Jim’s life- (fiberoptic) so that assistants will have access to CE pro- time of service to the grams statewide.
    [Show full text]
  • Biomechanics of Orthodontic Correction of Dental Asymmetries
    Biomechanics of orthodontic correction of dental asymmetries Edsard van Steenbergen, DDS, MDS" and Ravindra Nanda, BDS, MDS, PhD b Farmington, Conn. Correction of dental asymmetries requires special attention in orthodontic treatment. Several types of asymmetries are described, along with the biomechanics needed for correction. Treatment with different appliance designs that correct these asymmetries with the lowest level of negative contribution from side effects will be compared with conventional treatment. (AM J ORTHOD DENTOFAC ORTHOP 1995;107:618-24.) Asymmetries are commonly observed in matoid arthritis, 9 condylar hyperplasia, 2 cleft lip various combinations in orthodontic patients. The and cleft palate, 9 holoprosencephaly, 9 neurofibro- origin of these asymmetries can be skeletal, 15 den- matosis, 1° mandibular fractures, and drifting and tal, 6 soft tissue, 7 or a combination of these. 1'2'8'9 tipping of teeth. 6 Many possible causes for asymmetries have been Refined diagnostic tools, such as computerized reported in the literature, including hemifacial mi- tomographic images 3'11'12 and stereo photogramme- crosomia, 1 hemifacial hypertrophy,5 juvenile rheu- try,13 allow three-dimensional analyses of the cran- iofacial complex. These methods can generate, with the aid of a computer, a three-dimensional image of From the University of Connecticut. the patient's face. With a coordinate system, the bHead, Department of Orthodontics. asymmetries can be quantified. The most important "Fellow in Orthodontics. Copyright © 1995 by the American Association of Orthodontists. diagnostic tool, however, remains the clinical ex- 0889-5406/95/$3.00 + 0 8/1/51160 amination of the patient. Roentgenograms, such as Fig. 1.
    [Show full text]
  • Professor Ravindra Nanda Topic Proposal for Grand Fokus 2010
    ABSTRACT Biomechanics and Science Based Orthodontics Dr. Ravindra Nanda (1) Enhancing Esthetics with Targeted Mechanics a. Smile Dynamics: University of Connecticut Normative Study b. Management of deep bites c. Differential diagnosis and treatment of midline problems d. Management of occlusal plane problems e. Developing a mechanics plan f. Mechanics to avoid g. Application of cantilevers, intrusion arches and asymmetric mechanics h. Case reports (2) Multidisciplinary Treatment a. Lengthening alveolar bone with extrusive forces for missing laterals b. Preparing edentulous sites for implants with orthodontic mechanics c. Intruding supra erupted teeth to create vertical space for prosthesis in opposing arch d. Orthodontic management of patients with multiple agenesis (3) Management of Open Bite Patients a. Diagnosis ,treatment plan and options b. Pros and cons of various treatment modalities c. Biomechanics based simple smart wires to correct dental open bites d. Headgear, habit breaking appliances and elastics e. Application of bone plates and mini screws to correct open bites CV Brief Curriculum Vitae Dr. Ravindra Nanda is at present a UConn Alumni Endowed Chair, and Professor and Head of the Department of Craniofacial Sciences and Chair of the Division of Orthodontics, University of Connecticut, Farmington, Connecticut, U.S.A. He received his dental training from Lucknow University, India. He received his orthodontic training first at Lucknow, India and then from Nijmegen, The Netherlands and the University of Connecticut. He also received a Ph.D. for the University of Nijmegen. He was an Assistant Professor of Orthodontics at Loyola University, Illinois from 1970 to 1972 and since 1972 he has been associated with the University of Connecticut.
    [Show full text]
  • Dr. Takayuki Kuroda to Give Keynote Lecture at the 9Th IOC
    Volume 24, Issue 2 [ 2019 ] THE OFFICIAL NEWSLETTER OF THE WORLD FEDERATION OF ORTHODONTISTS Dr. Takayuki Kuroda to give keynote lecture at the 9th IOC he Organizing Committee of the 9th International Orthodontic of Orthodontics in the Faculty of Dentistry at the TMDU. From TConference, which will be October 4-7 in Yokohama, Japan, 1999-2002, he served as professor and chair of the Department of has announced that Dr. Takayuki Kuroda will be the meeting’s Maxillofacial Reconstruction at the university. keynote speaker giving the 2020 WFO Lecture. Dr. Kuroda is Professor Kuroda is a past president of the International Association professor emeritus of the Tokyo Medical and Dental University. for Dental Research. He received one of his country’s highest civilian The title of Dr. Kuroda’s lecture will be, “ Evidence-Based honors, The Order of the Sacred Treasure, Gold Rays with Neck Orthodontic Treatment, What Is It?” Ribbon. A graduate of the Tokyo Medical and Dental Dr. Kuroda served on the first WFO Executive Committee (1995- University (TMDU) in Tokyo, Japan, Dr. Kuroda 2000). He was named an Honorary Member of the WFO in 2010. subsequently received his orthodontic education 9th IOC Will Offer an Educational Program with Breadth and Depth and PhD from the Tokyo Medical and Dental University. After completing his PhD in 1966, Attendees at the IOC will enjoy outstanding speakers from he served as a research fellow at the Royal Dental throughout the world in a scientific program being developed by Dr. Takayuki Kuroda College in Copenhagen, Denmark and at the Center the Organizing Committee, led by Dr.
    [Show full text]