DOCSLIB.ORG

Gaia EDR3 View on Galactic Globular Clusters

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Gaia EDR3 View on Galactic Globular Clusters Gaia EDR3 view on Galactic globular clusters Eugene Vasiliev Institute of Astronomy, Cambridge 1 10 100 distance IAP seminar, 17 June 2021 based on: Vasiliev & Baumgardt (2102.09568), Baumgardt & Vasiliev (2105.09526) The Gaia [r]evolution all-sky photome- astrometry and improved preci- try: 109 stars colours: > 109, sion and reduced Vlos: 7M stars calibration errors with G . 13 Hipparcos + Gaia = TGAS (1989{1993) astrometry: 2M 22 months 34 months nearby stars DR1 =) DR2 =) EDR3 The Gaia [r]evolution all-sky photome- astrometry and improved preci- Vlos for fainter try: 109 stars colours: > 109, sion and reduced stars; binary pa- Vlos: 7M stars calibration errors rameters; epoch with G . 13 astrometry and Hipparcos + Gaia = TGAS photometry... (1989{1993) astrometry: 2M 22 months 34 months nearby stars pre-Gaia =) DR1 =) DR2 =) EDR3 =) DR3, 4, 5 Determination of cluster membership Determination of cluster membership Determination of cluster membership and parameters A hard cutoff in PM space is not always possible and is conceptually unsatisfactory. A more mathematically well-grounded alternative: mixture modelling [Gaussian or more general]. Write down the distribution functions for both cluster and field populations, and vary their parameters θ to maximize the likelihood of the observed data data: true DF convolved with errors measurements: $; µ; R measurement uncertainties XNstars ln L ≡ ln η fmemb(xi ;δ xi j θmemb) + (1 − η) ffield(xi ;δ xi j θfield) i=1 fraction of members parameters of distributions Results: cluster properties $; µ; σµ(R); µrot(R); η; : : : η fmemb(xi ) and membership probability of each star: pi = . η fmemb(xi ) + (1 − η) ffield(xi ) 6d kinematics of star clusters typical PM uncertainty: δµ ' 0:025 mas/yr distance uncertainty: ∼ a few percent v µ D = 4:74 km=s mas=yr kpc distance uncertainty usually dominates 100 AM 1 AM 4 Crater orbits for the last 100 Myr 50 Munoz 1 Pal 3 Laevens 3 Ko 1 Ko 2 Pal 4 20 Eridanus Pal 14 NGC 2419 10 5 104 2 103 velocity uncertainty 2 1 10 1 0.5 10 number of stars 2 5 10 20 50 100 orbits for the last 10 Gyr distance [Kpc] Orbits of star clusters NGC 6712 M 79 M 72 1.0 NGC 362 NGC 4147 Pal 14 1.0 NGC 1851 NGCNGC 6287 5946 NGC 6229 Pal 6 M 92 Pal 2 NGC 7006 NGC 6642 Pal 15 M 2 UKS 1 IC 1257 NGC 5694 Pal 4 NGC 5286 NGC 2298 NGC 1261 NGC 6401 M 75 NGC 6638VVV CL002 NGCM 6544 70 NGC 6355 NGC 6934 NGC 4833 M 56 NGC 5986 NGC 6284 ESO 280 NGC 2808 ESO 452 M 4 NGC 7492 NGC 6584 Eridanus NGC 6528 Ryu 879 M 5 NGC 6293 Liller 1 NGC 5634 M 9 NGC 2419 NGC 6652 M 19 Djorg 1 Terzan 10 Pal 13 AM 1 0.8 NGC 6453 M 13 NGC 6558 M 14 NGC 6440 Terzan 9 Laevens 3 NGC 6380 NGC 6517 M 30 NGC 288 Rup 106 NGC 5466 Ryu 059 Terzan 5 0.5 BH 229 M 28 M 55 M 80 BH 140 Pyxis ω NGC 6426 VVV CL001 NGC 6316 C Kim 3 e ) n NGC 5897 FSR 1758 IC 4499 L Terzan 1 NGC 6535 NGC 6624 0.6 / z M 22 Terzan 6 M 107 NGC 6139 L Gran 1 Pal 8 NGC 6749 NGC 6101 Terzan 7 ( NGCNGCFSR 63886541 1735 Pal 12 Terzan 8 M 62 NGC 6366 M 3 NGC 3201 M 68 M 54 n Terzan 4 0.0 o NGC 6144 Whiting 1 i NGC 6723 NGC 6441 Mercer 5 NGC 6397 Arp 2 M 15 t BHM 184 10 NGC 6760 NGC 6325 NGC 4372 M 53 NGC 6342 a NGC 6522 NGCNGC 6235 6356 Pal 9 n M 12 NGC 5824 i BH 261 l eccentricity Terzan 2 0.4 c NGC 6496 NGC 6362 n FSR 1716 i Terzan 12 Ton 2 Pfleiderer 2 Pal 3 Djorg 2 NGC 6540 Pal 7 Bliss 1 Pal 5 M 69 NGC 6304 NGC 5053 Ko 2 Pal 11 NGC 6752 Pal 10 Ko 1 NGC 6539 Munoz 1 0.5 Terzan 3 NGC 6256 0.2 NGC 6569 M 71 BH 176 Crater NGC 6553 47 Tuc E 3 NGC 5927 Pal 1 NGC 6352 ESO 93-8 Segue 3 AM 4 0.0 1.0 0.7 1 2 3 5 7 10 20 30 50 70 100 semimajor axis [kpc] Clusters in the space of integrals of motion polar 5 10 20 50 100 EDR3 semimajor axis [kpc] DR2 Ko 1 NGC 5053 Sagittarius 0 NGC 5053 → [Law&Majewski 2010, . ] circular Terzan 7 Terzan 8 y Pal 5 t i M 53 WhitingArp 2 M 53 1 Pal 5 Arp 2 Terzan 8 M 54 c circular Terzan 7 M 54 i r Whiting 1 t Kim 3 180 ◦ inclination 0 ◦ n ← → NGC 5824 NGC 5824 e c Pal 12 NGC 5897 NGC 5897 NGC 6235 c Pyxis M 3 M 3 Pal 12 NGC 6235 Pyxis e 47 Tuc 47 Tuc IC 4499 IC 4499 M 30 Segue 3 prograde M 30 E 3 NGC 6397 E 3 Pal 11 ← NGC 6397 NGC 6356 NGC 6287 NGC 6356 Pal 11 M 13 Pal 1 NGC 6284 NGC 288 NGC 7492 1 Terzan 10 Pal 1 NGC 288 Ko 2 M 68 M 13 M 68 Bliss 1 FSR 1716 M 15 M 71 Terzan 10 Pfleiderer 2 NGCM 592771 M 15 NGC 5466 ESO 93-8 BH 176 NGC 5466 BH 176 NGC 6101 NGC 6284 Pal 10 Pal 7 Pal 10 NGC 6101 NGC 6496 NGC 4372 Pal 7 NGC 3201 M 92 NGC 4372 NGC 3201 ω M 22 M 22 retrograde C FSR 1758e NGC 5634 n NGC 5634 NGC 7492 Pal 13 ω M 5 M 5 C Pal 13 e M 92 M 9 M 9 NGC 6426 n NGC 6426 ESO 280 NGC 362 NGC 1261 Rup 106 Rup 106 ESO 280 M 56 NGC 2298 BH 140 NGC 6584 M 75 NGC 6584 NGC 4147NGC 362 Ryu 059 M 75 NGC 1261 NGC 2298 in-plane NGC 5286 NGC 4147 IC 1257 NGC 5286 M 56 M 2 NGC 4833 M 2 NGC 4833 Djorg 1 Djorg 1 NGC 7006 NGC 5694 NGC 6229 NGC 6229 NGC 1851 Pal 15 in-plane NGC 7006 NGC 5694 NGC 1851 NGC 6934 NGC 6934 UKS 1 radially M 72 NGC 2808 NGC 2808 IC 1257 Sequoia M 72 anisotropic M 79 M 79 [Myeong+ 2019] Pal 14 Pal 2 population [Myeong+ 2018, Pal 2 radial Helmi+ 2018] Clusters in the space of integrals of motion Jackson Pollock, \Convergence" Kliment Redko, \Uprising" Distances to star clusters compilation of ∼ 1300 measurements from literature by Holger Baumgardt (CMD, RR Lyrae, eclipsing binaries) + HST/Gaia dynamical fits & parallaxes Internal kinematics: rotation, dispersion Good agreement with HST µ σ rot µ σ µ [Watkins+ 2015, Cohen+ 2021] 0.6 NGC 104 (47 Tuc) NGC 288 NGC 6838 (M 71) 3.5 N=39931 (33144), D=4.5 kpc 0.08 N=4690 (226), D=9.0 kpc N=3021 (833), D=4.0 kpc 3 0.15 10 3.0 ] 0.4 ] ] r r 0.06 r y y 2.5 y ] ] ] / / / s s s s s s 0.10 2 a a a 5 / 2.0 / / m m m m m m [ 0.2 [ [ k k k [ 0.04 [ [ µ µ µ s 1.5 s s σ σ σ o o o l l l , , , σ σ σ t t t 0.05 1 o o o r r 1.0 r µ 0.0 0 µ 0.02 µ 0.5 0.00 0 0.2 0.00 0.0 5 0 5 10 15 20 25 30 35 40 0 2 4 6 8 10 12 14 0 2 4 6 8 10 R [arcmin] R [arcmin] R [arcmin] and 25 NGC 5139 (ω Cen) NGC 4590 (M 68) 0.20 NGC 6681 (M 70) 0.10 5 N=53122 (37288), D=5.4 kpc N=3284 (148), D=10.4 kpc N=857 (48), D=9.4 kpc 8 σ 0.8 20 0.08 4 0.15 LOS ] ] ] r r r 6 y y y ] ] ] / / / s s s s 0.6 15 s 0.06 3 s a a a / / 0.10 / m m m m m m from literature [ [ [ k k 4 k [ 2 [ [ µ µ µ 0.04 s s s σ σ σ o o o l l l 0.4 , 10 , , σ σ σ t t t o o o 0.05 r r 0.02 1 r 2 µ µ µ 0.2 5 0.00 0 0.00 0 0.02 1 0.0 0 0 5 10 15 20 25 30 35 40 0 2 4 6 8 10 12 14 0 1 2 3 4 5 6 R [arcmin] R [arcmin] R [arcmin] PM anisotropy profiles 0.3 NGC 104 0.3 NGC 3201 0.3 NGC 6218 1 0.2 1 0.2 1 0.2 − 0.1 − 0.1 − 0.1 R R R tangential , , , µ 0.0 µ 0.0 µ 0.0 σ σ σ $ / / / t 0.1 t 0.1 t 0.1 , , , µ 0.2 µ 0.2 µ 0.2 σ σ σ 0.3 radial 0.3 0.3 0 5 10 15 20 25 30 0 5 10 15 20 0 2 4 6 8 Radius [arcmin] Radius [arcmin] Radius [arcmin] 0.3 NGC 5139 0.3 NGC 6121 0.1 NGC 7078 1 0.2 1 0.2 1 0.0 − 0.1 − 0.1 − 0.1 R R R , , , µ 0.0 µ 0.0 µ 0.2 σ σ σ / / / t 0.1 t 0.1 t 0.3 , , , µ 0.2 µ 0.2 µ 0.4 σ σ σ 0.3 0.3 0.5 0 5 10 15 20 25 30 35 0 5 10 15 20 0 2 4 6 8 Radius [arcmin] Radius [arcmin] Radius [arcmin] variety of profiles, mostly weakly radial or isotropic Perspective effects in the radial PM component Perspective contraction/expansion due to line-of-sight motion: ◦ µR (R) = ξ R; ξexpected = −vLOS=D × (π=180 =4:74) mas/yr/degree.
Load more

Recommended publications
  • Spatial Distribution of Galactic Globular Clusters: Distance Uncertainties and Dynamical Effects
    Juliana Crestani Ribeiro de Souza Spatial Distribution of Galactic Globular Clusters: Distance Uncertainties and Dynamical Effects Porto Alegre 2017 Juliana Crestani Ribeiro de Souza Spatial Distribution of Galactic Globular Clusters: Distance Uncertainties and Dynamical Effects Dissertação elaborada sob orientação do Prof. Dr. Eduardo Luis Damiani Bica, co- orientação do Prof. Dr. Charles José Bon- ato e apresentada ao Instituto de Física da Universidade Federal do Rio Grande do Sul em preenchimento do requisito par- cial para obtenção do título de Mestre em Física. Porto Alegre 2017 Acknowledgements To my parents, who supported me and made this possible, in a time and place where being in a university was just a distant dream. To my dearest friends Elisabeth, Robert, Augusto, and Natália - who so many times helped me go from "I give up" to "I’ll try once more". To my cats Kira, Fen, and Demi - who lazily join me in bed at the end of the day, and make everything worthwhile. "But, first of all, it will be necessary to explain what is our idea of a cluster of stars, and by what means we have obtained it. For an instance, I shall take the phenomenon which presents itself in many clusters: It is that of a number of lucid spots, of equal lustre, scattered over a circular space, in such a manner as to appear gradually more compressed towards the middle; and which compression, in the clusters to which I allude, is generally carried so far, as, by imperceptible degrees, to end in a luminous center, of a resolvable blaze of light." William Herschel, 1789 Abstract We provide a sample of 170 Galactic Globular Clusters (GCs) and analyse its spatial distribution properties.
    [Show full text]
  • A Basic Requirement for Studying the Heavens Is Determining Where In
    Abasic requirement for studying the heavens is determining where in the sky things are. To specify sky positions, astronomers have developed several coordinate systems. Each uses a coordinate grid projected on to the celestial sphere, in analogy to the geographic coordinate system used on the surface of the Earth. The coordinate systems differ only in their choice of the fundamental plane, which divides the sky into two equal hemispheres along a great circle (the fundamental plane of the geographic system is the Earth's equator) . Each coordinate system is named for its choice of fundamental plane. The equatorial coordinate system is probably the most widely used celestial coordinate system. It is also the one most closely related to the geographic coordinate system, because they use the same fun­ damental plane and the same poles. The projection of the Earth's equator onto the celestial sphere is called the celestial equator. Similarly, projecting the geographic poles on to the celest ial sphere defines the north and south celestial poles. However, there is an important difference between the equatorial and geographic coordinate systems: the geographic system is fixed to the Earth; it rotates as the Earth does . The equatorial system is fixed to the stars, so it appears to rotate across the sky with the stars, but of course it's really the Earth rotating under the fixed sky. The latitudinal (latitude-like) angle of the equatorial system is called declination (Dec for short) . It measures the angle of an object above or below the celestial equator. The longitud inal angle is called the right ascension (RA for short).
    [Show full text]
  • Abundances for Globular Cluster Giants
    A&A manuscript no. (will be inserted by hand later) ASTRONOMY AND Your thesaurus codes are: ASTROPHYSICS (08.01.1; 08.01.03; 08.16.3; 10.07.3) 24.8.2017 Abundances for Globular Cluster Giants: I. Homogeneous Metallicities for 24 Clusters E. Carretta1,3, R. G. Gratton2 1 Osservatorio Astronomico di Bologna, Via Zamboni 33, I-40126 Bologna, ITALY 2 Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, I-35122 Padova, ITALY 3 Dipartimento d’Astronomia, Universit`adi Padova, Vicolo dell’Osservatorio 5, I-35122 Padova, ITALY Received 28 February 1996/Accepted 21 May 1996 Abstract. We have obtained high resolution, high signal- calibration of the ∆S index) and our new cluster metallici- to-noise ratio CCD echelle spectra of 10 bright red giants ties. It could be tentatively ascribed to non-linearity in the in 3 globular clusters (47 Tuc, NGC 6752 and NGC 6397) [Fe/H]−∆S relationship. The impact of new metallicities roughly spanning the whole range of metallicities of the on major astrophysical problems is exemplified through galactic globular cluster system. The analysis of this newly a simple exercise on the Oosterhoff effect in the classical acquired material reveals no significant evidence of star- pair M 3 and M 15. to-star variation of the [Fe/H] ratio in these three clusters. Moreover, a large set of high quality literature data (equiv- Key words: Stars: abundances - Stars: Atmospheres - alent widths from high dispersion CCD spectra) was re- Stars: Population II - globular clusters: general analyzed in an homogeneous and self-consistent way to in- tegrate our observations and derive new metal abundances for more than 160 bright red giants in 24 globular clusters (i.e.
    [Show full text]
  • Arxiv:1911.02835V1 [Astro-Ph.SR] 7 Nov 2019 Astronomy, Monash University, Melbourne, Clayton 3800, Australia
    The Astronomy and Astrophysics Review manuscript No. (will be inserted by the editor) What is a Globular Cluster? An observational perspective Raffaele Gratton1 · Angela Bragaglia2 · Eugenio Carretta2 · Valentina D’Orazi1;3 · Sara Lucatello1 · Antonio Sollima2 Received: date / Accepted: date Abstract Globular clusters are large and dense agglomerate of stars. At variance with smaller clusters of stars, they exhibit signs of some chemical evolution. At least for this reason, they are intermediate between open clusters and massive objects such as nuclear clusters or compact galaxies. While some facts are well established, the increasing amount of observational data is revealing a complexity that has so far de- fied the attempts to interpret the whole data set in a simple scenario. We review this topic focusing on the main observational features of clusters in the Milky Way and its satellites. We find that most of the observational facts related to the chemical evo- lution in globular clusters are described as being primarily a function of the initial mass of the clusters, tuned by further dependence on the metallicity – that mainly affects specific aspects of the nucleosynthesis processes involved – and on the envi- ronment, that likely determines the possibility of independent chemical evolution of the fragments or satellites where the clusters form. We review the impact of multiple populations on different regions of the colour-magnitude diagram and underline the constraints related to the observed abundances of lithium, to the cluster dynamics, and to the frequency of binaries in stars of different chemical composition. We then re-consider the issues related to the mass budget and the relation between globular cluster and field stars.
    [Show full text]
  • The Messier Objects
    Warren H. Finlay Concise Catalog of Deep-Sky Objects Astrophysical Information for 550 Galaxies, Clusters and Nebulae Second Edition The Patrick Moore The Patrick Moore Practical Astronomy Series For further volumes: http://www.springer.com/series/3192 Concise Catalog of Deep-Sky Objects Astrophysical Information for 550 Galaxies, Clusters and Nebulae Warren H. Finlay Second Edition Warren H. Finlay Edmonton , AB , Canada ISSN 1431-9756 ISSN 2197-6562 (electronic) ISBN 978-3-319-03169-9 ISBN 978-3-319-03170-5 (eBook) DOI 10.1007/978-3-319-03170-5 Springer Cham Heidelberg New York Dordrecht London Library of Congress Control Number: 2014938104 © Springer International Publishing Switzerland 2003, 2014 This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifi cally the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfi lms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed. Exempted from this legal reservation are brief excerpts in connection with reviews or scholarly analysis or material supplied specifi cally for the purpose of being entered and executed on a computer system, for exclusive use by the purchaser of the work. Duplication of this publication or parts thereof is permitted only under the provisions of the Copyright Law of the Publisher’s location, in its current version, and permission for use must always be obtained from Springer. Permissions for use may be obtained through RightsLink at the Copyright Clearance Center.
    [Show full text]
  • The Origin of Globular Cluster FSR 1758 Fu-Chi Yeh1, Giovanni Carraro1, Vladimir I
    A&A 635, A125 (2020) Astronomy https://doi.org/10.1051/0004-6361/201937093 & c ESO 2020 Astrophysics The origin of globular cluster FSR 1758 Fu-Chi Yeh1, Giovanni Carraro1, Vladimir I. Korchagin2, Camilla Pianta1, and Sergio Ortolani1 1 Department of Physics and Astronomy Galileo Galilei, Vicolo Osservatorio 3, 35122 Padova, Italy e-mail: [email protected] 2 Southern Federal University, Rostov on Don, Russian Federation Received 10 November 2019 / Accepted 5 February 2020 ABSTRACT Context. Globular clusters in the Milky Way are thought to have either an in situ origin, or to have been deposited in the Galaxy by past accretion events, like the spectacular Sagittarius dwarf galaxy merger. Aims. We probe the origin of the recently discovered globular cluster FSR 1758, often associated with some past merger event and which happens to be projected toward the Galactic bulge. We performed a detailed study of its Galactic orbit, and assign it to the most suitable Galactic component. Methods. We employed three different analytical time-independent potential models to calculate the orbit of the cluster by using the Gauss Radau spacings integration method. In addition, a time-dependent bar potential model is added to account for the influence of the Galactic bar. We ran a large suite of simulations via a Montecarlo method to account for the uncertainties in the initial conditions. Results. We confirm previous indications that the globular cluster FSR 1758 possesses a retrograde orbit with high eccentricity. The comparative analysis of the orbital parameters of star clusters in the Milky Way, in tandem with recent metallicity estimates, allows us to conclude that FSR 1758 is indeed a Galactic bulge intruder.
    [Show full text]
  • Ssp-Deep-Sky-Challenge V2.Indd
    Deep Sky Observer’s Challenge presented at the Southern Star Party The Deep Sky Observer’s Challenge The SSP Deep Sky Observer’s Challenge has been designed to challenge your observing skills no matter your level of expertise. Meeting the challenge is not about quantity, but about quality, so it doesn’t matter if you’re using small binoculars or a 24-inch computer-controlled telescope. For the Beginner’s Challenge, a basic description (with or without a diagram) is adequate. If you know how, you could also indicate the apparent angular size of the object. To meet the Beginner’s Challenge, you will need to observe and adequately describe ten objects. Feel free to record more! For the Intermediate Challenge, you’ll need to include angular size and, where appropriate, direction (either estimating the position angle or by using cardinal directions), in your description. If you know how, you could also include a magnitude estimate. To meet the Intermediate Challenge, you will need to observe and adequately describe twenty-five objects. Feel free to record more! For the Advanced Challenge, you’ll need to include, in addition to the attributes mentioned above, an estimate of magnitude. To meet the Advanced Challenge, you will need to observe and properly describe 110 objects from the list. Part of the challenge is preparing for the night’s observing. Only observations made during the duration of the star party are eligible for consideration, so you’ll have to do some planning beforehand.Planning would include selecting suitable objects from the list: will they be visible during the challenge period? I would suggest you select more than the minimum number of objects needed: the more the merrier! You will also need suitable star charts to help you locate the objects.
    [Show full text]
  • Arxiv:1201.6526V1 [Astro-Ph.SR]
    Noname manuscript No. (will be inserted by the editor) Multiple populations in globular clusters Lessons learned from the Milky Way globular clusters Raffaele G. Gratton · Eugenio Carretta · Angela Bragaglia Received: date / Accepted: date Abstract Recent progress in studies of globular clusters has shown that they are not simple stellar populations, being rather made of multiple generations. Evidence stems both from photometry and spectroscopy. A new paradigm is then arising for the formation of massive star clusters, which includes sev- eral episodes of star formation. While this provides an explanation for several features of globular clusters, including the second parameter problem, it also opens new perspectives about the relation between globular clusters and the halo of our Galaxy, and by extension of all populations with a high specific frequency of globular clusters, such as, e.g., giant elliptical galaxies. We review progress in this area, focusing on the most recent studies. Several points re- main to be properly understood, in particular those concerning the nature of the polluters producing the abundance pattern in the clusters and the typical timescale, the range of cluster masses where this phenomenon is active, and the relation between globular clusters and other satellites of our Galaxy. Keywords Galaxy: general · Globular Clusters · halo · Stars: abundances · Hertzsprung-Russell and C-M diagrams R.G. Gratton INAF - Osservatorio Astronomico di Padova Phone: +39-049-8293442 Fax: +39-049-8759840 E-mail: raff[email protected] E. Carretta INAF - Osservatorio Astronomico di Bologna Phone: +39-051-2095776 E-mail: eugenio [email protected] A. Bragaglia arXiv:1201.6526v1 [astro-ph.SR] 31 Jan 2012 INAF - Osservatorio Astronomico di Bologna Phone: +39-051-2095770 E-mail: [email protected] 2 R.G.
    [Show full text]
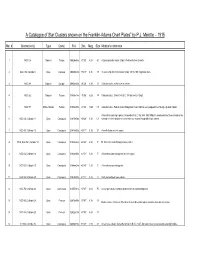
  • A Catalogue of Star Clusters Shown on the Franklin-Adams Chart Plates” by P.J
    A Catalogue of Star Clusters shown on the Franklin-Adams Chart Plates” by P.J. Melotte – 1915 Mel. # Alternative(s) Type Const. R.A. Dec. Mag. Size Melotte's comments 1 NGC 104 Globular Tucana 00h24m04s -72°05' 4.00 50' A typical globular cluster. Bright. Well condensed at centre. 2 NGC 188, Collinder 6 Open Cepheus 00h47m28s +85°15' 9.30 17' "A somewhat ill-defined cluster mostly 14th to 16th magnitude stars. 3 NGC 288 Globular Sculptor 00h52m45s -26°35' 8.10 13' Globular cluster, rather loose at centre. 4 NGC 362 Globular Tucana 01h03m14s -70°50' 6.80 14' Globular cluster. Similar to N.G.C. 104 but smaller. Bright. 5 NGC 371 Diffuse Nebula Tucana 01h03m30s -72°03' 13.80 7.5' Globular cluster. Falls in smaller Magellanic cloud, and has every appearance of being a globular cluster. A few stars clustering together. Resembles N.G.C. 582, 645, 659. Difficult to decide whether these should not be 6 NGC 436, Collinder 11 Open Cassiopeia 01h15m58s +58°48' 9.30 5.0' classed II. All the clusters here resemble one another though differing in extent. 7 NGC 457, Collinder 12 Open Cassiopeia 01h19m35s +58°17' 5.10 20' A small cluster in a rich region. 8 M103, NGC 581, Collinder 14 Open Cassiopeia 01h33m23s +60°39' 6.90 5' M. 103. A few stars forming a loose cluster. 9 NGC 654, Collinder 18 Open Cassiopeia 01h44m00s +61°53' 8.20 5' A few stars clustered together in a rich region. 10 NGC 659, Collinder 19 Open Cassiopeia 01h44m24s +60°40' 7.20 5' A few stars clustered together.
    [Show full text]
  • 7.5 X 12.5 Long Title.P65
    Cambridge University Press 978-0-521-89936-9 - Cosmic Challenge: The Ultimate Observing List for Amateurs Philip S. Harrington Index More information Index 16+17 Draconis, 92–3 CGCG 89–56, 369 IC 4614, 327 30 Arietis, 113 CGCG 89–62, 369 IC 4616, 326 3C273, 141–2 Cocoon Nebula, 161–3 IC 4617, 326 61 Cygni, 159–60 Collinder 470, 163 IC 4732, 330–1 Abell 12, 358–9 Copeland’s Septet, 380–1 IC 4997, 248–9 Abell 33, 308–9 Crab Nebula, 118–19 IC 5067, 104 Abell 36, 319–20 IC 5070, 104 Abell 70, 335–6 Dark Horse Nebula, 41–3 IC 5146, 161–3 Abell Galaxy Cluster 373, 271–3 Dawes’ Limit, 13 IC 5217, 252–3 Abell Galaxy Cluster 426, 355–7 Deer Lick Group, 254–6 IRAS 18333–2357. See PK 9–7.1 Abell Galaxy Cluster 1060, 313–16 Double Cross. See Leo Trio Izar, 145–6 Abell Galaxy Cluster 1367, 382–6 double stars (table), 463–6 Abell Galaxy Cluster 1656, 387–91 Dumbbell Nebula, 97 Jonckheere 320, 274–5 Abell Galaxy Cluster 2065, 392–4 Jonckheere 900, 186–7 Abell Galaxy Cluster 2151, 398–401 Einstein’s Cross, 420–2 Jones-Emberson 1. See PK 164+31.1 Alcor. See Mizar Elephant’s Trunk Nebula, 418–19 Andromeda Galaxy, 51–3 Epsilon Bootis.¨ See Izar K648. See Pease 1 Antennae, The, 228–9 exit pupil, 15 Kratz’s Cascade, 281 Arp 41, 352–4 eye, human, 2 Arp 77, 349–51 eyepieces, 14–17 Lambda Arietis, 113 Arp 82, 362–3 apparent field of view, 16 Lambda Cassiopeiae, 261–3 averted vision, 3 color, 17 Leo I, 371–3 deep-sky, 17–20 Leo II, 374–5 Barnard 33, 184–5 filters, 17–20 Leo Trio, 88–9 Barnard 59.
    [Show full text]
  • The Southern Hemisphere
    R O T H N MAJOR URSA T THE SOUTHERN HEMISPHERE S AURIGA E N W O LYNX H With Glenn Dawes R T T R H β O E A Spot the peak of the Alpha Centaurid meteor N M36 GEMINI S T α shower and enjoy a view of the stars in Orion’s Belt LEO MINOR LEO Almach Castor α M37 CANCER Pollux γ β When to use this chart M35 ANDROMEDA 22nd β M44 Beehive M44 Sickle The chart accurately matches the sky on the 1 Feb at 00:00 AEDT (13:00 UT) LEO δ dates and times shown for Sydney, Australia. γ γ 25th 15 Feb at 23:00 AEDT (12:00 UT) δ The sky is different at other times as the stars δ 31 Feb at 22:00 AEDT (11:00 UT) crossing it set four minutes earlier each night. X γ BERENICES Ecliptic Rosette Nebula Rosette M64 Betelgeuse COMA CANIS MINOR CANIS α Regulus α δ M66 M86 β α β FEBRUARY HIGHLIGHTS STARS AND CONSTELLATIONS “V” 28th M87 Aldebaran α β δ ORION The Alpha Centaurids is one of the The three distinctive Belt stars of α γ Winter Triangle Winter Procyon Alpheratz few meteor showers that’s exclusive Orion are possibly the most easily Hyades to the Southern Hemisphere. Active from recognised asterism visible from anywhere M60 α M49 HYDRA γ δ 31 January to 20 February, its peak is in the world. From left to right (west β M78 st 1 VIRGO δ TAURUS MONOCEROS expected on the 8th.
    [Show full text]
  • Gas Expulsion in Massive Star Clusters? Constraints from Observations of Young and Gas-Free Objects
    A&A 587, A53 (2016) Astronomy DOI: 10.1051/0004-6361/201526685 & c ESO 2016 Astrophysics Gas expulsion in massive star clusters? Constraints from observations of young and gas-free objects Martin G. H. Krause1,2,3, Corinne Charbonnel4,5, Nate Bastian6, and Roland Diehl2,3 1 Universitäts-Sternwarte München, Ludwig-Maximilians-Universität, Scheinerstr. 1, 81679 München, Germany e-mail: [email protected] 2 Max-Planck-Institut für extraterrestrische Physik, Giessenbachstr. 1, 85741 Garching, Germany 3 Excellence Cluster Universe, Technische Universität München, Boltzmannstrasse 2, 85748 Garching, Germany 4 Geneva Observatory, University of Geneva, 51 Chemin des Maillettes, 1290 Versoix, Switzerland 5 IRAP, UMR 5277 CNRS and Université de Toulouse, 14 Av. E. Belin, 31400 Toulouse, France 6 Astrophysics Research Institute, Liverpool John Moores University, 146 Brownlow Hill, Liverpool L3 5RF, UK Received 6 June 2015 / Accepted 13 December 2015 ABSTRACT Context. Gas expulsion is a central concept in some of the models for multiple populations and the light-element anti-correlations in globular clusters. If the star formation efficiency was around 30 per cent and the gas expulsion happened on the crossing timescale, this process could preferentially expel stars born with the chemical composition of the proto-cluster gas, while stars with special composition born in the centre would remain bound. Recently, a sample of extragalactic, gas-free, young massive clusters has been identified that has the potential to test the conditions for gas expulsion. Aims. We investigate the conditions required for residual gas expulsion on the crossing timescale. We consider a standard initial mass function and different models for the energy production in the cluster: metallicity-dependent stellar winds, radiation, supernovae and more energetic events, such as hypernovae, which are related to gamma ray bursts.
    [Show full text]