DOCSLIB.ORG

Intersection Safety Strategies Brochure (FHWA)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

SIGNALIZED INTERSECTION SAFETY STRATEGIES CATEGORY A: REDUCE CATEGORY D: IMPROVE DRIVER 2013 INTERSECTION FATALITIES FREQUENCY AND SEVERITY AWARENESS OF INTERSECTIONS OF INTERSECTION CONFLICTS AND SIGNAL CONTROL THROUGH TRAFFIC CONTROL lD1 – Improve visibility of intersections Signalized 3,338 AND OPERATIONAL on approach(es) IMPROVEMENTS Where to use - Signalized intersections with a high frequency of crashes attributed to Unsignalized 5,760 lA1 – Replace permissive left turns drivers being unaware of the presence of the with protected left turns intersection. Where to use - Signalized intersections with a high frequency of angle crashes ? Other/Unknown 235 involving left turning and opposing through vehicles. A properly timed protected left- lD2 – Improve visibility of signals and signs at intersections turn phase can also help reduce rear-end and sideswipe crashes between left-turning Where to use -Signalized intersections with a high frequency of right-angle and 0 1,000 2,000 3,000 4,000 5,000 6,000 vehicles and the through vehicles behind them. rear-end crashes occurring because drivers are unable to see traffic signals and signs Source: FARS, National Highway Traffic Safety Administration (2013). Available: http://safety.fhwa.dot.gov/intersection/resources/intsafestratbro/intersection_guide12.pdf Keywords: protected, permissive, signal phasing SIG sufficiently in advance to safely negotiate the intersection being approached. Keywords: signal visibility SIG lA2 – Optimize change and clearance intervals SIGNALIZED COST Where to use - Signalized intersections with a high frequency of crashes related to lD3 – Install/add one signal head per lane change interval lengths that are possibly too short. These crashes include angle Where to use - Signalized intersections with a high frequency of crashes caused by SAFETY CONCERN lLow lModerate lHigh High frequency of right-angle crashes crashes between vehicles continuing through the intersection after one phase has driver indecision in lane assignment. SIG ended and the vehicles entering the intersection on the following phase. Rear-end Keywords: add signal, signal head attributed to: crashes may also be a symptom of short change intervals. nearby driveways F2 F1 Keywords: change interval, signal phasing, signal timing SIG lD4 – Install larger 12” signal heads traffic from cross street A2, A3 E2 Where to use - Signalized intersections with a crash history or observed conflicts skewed intersection lA3 – Restrict or eliminate turning maneuvers involving lack of awareness of the intersection or traffic control and observed speeding Where to use - Signalized intersections with a high frequency of crashes related to on approaches to the intersection. poor sight distance A1, C1, G5 C2, G4 B3 Keywords: signal lense, signal head SIG turning maneuvers. For right turn on red (RTOR), the target of this strategy is right- drivers misjudging gaps A1 turning vehicles that are involved in rear-end or angle crashes with cross-street vehicles not enough gaps for drivers A1 A4, B4 approaching from the left or vehicles turning left from the opposing approach, and lD5 – Install signal backplate/retroreflective backplates crashes involving pedestrians. Where to use - Signalized intersections with poor visibility of the intersection from driver unaware of intersection D1, D2, D5, D6 C2 B4 Keywords: right turn on red PED SIG approaches, a crash history or observed conflicts involving lack of awareness of the intersection or traffic control, and observed speeding on approaches to the nighttime conditions D1, D2, D5 intersection. right turning vehicles hit from side A3, C1, G5 B1, G4 lA4 – Employ signal coordination P Where to use - Signalized intersections with a high frequency of crashes involving Keywords: retroreflective, backplate High frequency of rear-end crashes major street left-turning and minor street right-turning vehicles where adequate safe attributed to: D6 – Install intersection warning devices gaps in opposing traffic are not available. Major road rear-end crashes associated with l left turning vehicles hit from behind A1 B1 B3 Where to use - Signalized intersections with poor visibility of the intersection from speed changes can also be reduced by re-timing signals to promote platooning. left opposing vehicles hit from behind B1 B3 Keywords: signal coordination, signal timing, cycles approaches, conflicts involving lack of awareness of the intersection or traffic control, PED and observed speeding on approaches to the intersection. Intersection warning right turning vehicles hit from behind A3 B1, B5 devices can include warning signs, beacons, and transverse rumble strips. lA5 – Employ emergency vehicle preemption standing water on roadway G1 Where to use - Signalized intersections where normal traffic operations impede Keywords: advance warning sign, positive guidance BIKE PED vehicles unable to stop safely (skidding) G2 emergency vehicles and where traffic conditions create a potential for conflicts D7 – Convert pole mounted to overhead signals between emergency and non-emergency vehicles. l driver unaware of intersection D1, D2, D5 D3, D4, D8 D7 Where to use - Signalized intersections with poor visibility of the intersection from approaches, a crash history or observed conflicts involving lack of awareness of nighttime conditions D1, D2, D5 D4 D7 A6 – Remove unwarranted signal l the intersection or traffic control, and observed speeding on approaches to the Where to use - Signalized intersections where the traffic volumes and safety record do speed differentials of vehicles A4, E3 intersection. not warrant a traffic signal. sudden stops A2, A3 A4, D3 Keywords: convert signal, pedestal mounted, mast arm Keywords: unwarranted, remove signal High frequency of left-turn crashes D8 – Install supplemental pole-mounted signal on near-side approach attributed to: A7 – Change green signal to flashing yellow arrow for permissive left turns l l Where to use - Signalized intersections with poor visibility of the intersection from left turn vehicles hit by opposing traffic A1, A3, A7, C1 B1, B4 B3 Where to use - Signalized intersections with high frequency of angle crashes involving approaches, a crash history or observed conflicts involving lack of awareness of left-turning and opposing through vehicles. The flashing yellow arrow (FYA) can be nighttime conditions D1, D2, D5 the intersection or traffic control, and observed speeding on approaches to the used in place of the simple circular green light and other signals to help convey the High frequency of sideswipe crashes intersection. attributed to: message that left-turning drivers need to yield to on-coming traffic. Keywords: add signal, signal head SIG Keywords: FYA, flashing yellow arrow, phasing, left turn, protected, permissive vehicles within intersection A1 B1 High frequency of pedestrian/bicycle lA8 – Install/implement pedestrian signal improvements crashes: Where to use - Signalized intersections with conflicts between vehicles and CATEGORY E: IMPROVE on school routes or near generators of ped/ A8 B2, E2 pedestrians crossing at the intersection, high volume of crossing pedestrians or DRIVER COMPLIANCE WITH bike traffic bicyclists, vehicles not yielding to pedestrians in crosswalk, and high pedestrian TRAFFIC CONTROL DEVICES vehicle/bicycle sideswipes on approaches A9, G1 delay due to few available gaps in traffic. Measures can include increasing pedestrian clearance intervals (or increasing the cycle length for pedestrian crossing), lE1 – Provide public information and with left turning vehicles A1, A3 A9 implementing leading pedestrian interval and installing pedestrian pushbuttons and education Address overall safety issues: pedestrian countdown signals. Where to use - Signalized intersections violation of traffic laws E1 A9, E2 Keywords: pedestrian, crossing, cycle length, signal phasing, pedestrian interval, countdown PED with a high frequency of crashes related to drivers either being unaware of (or refusing intersection near railroad crossing G3 to obey) traffic laws and regulations that impact traffic safety (especially red-light lA9 – Install bicycle signal intersection near fire station Where to use - Signalized intersections with conflicts between vehicles and bicycles running, speeding, and not yielding to pedestrians). BIKE PED A5 crossing at the intersection, high volume of bicyclists, vehicles not yielding to bicyclists. excessive delay A6 E2 – Provide targeted conventional enforcement of traffic laws l disobedience of traffic signal BIKE Where to use -Signalized intersections with a high frequency of crashes related to A6 A9, D3, D8 drivers either being unaware of (or refusing to obey) traffic laws and regulations that CATEGORY B: REDUCE impact traffic safety. BIKE PED SIG INTERSECTION CONFLICTS lE3 – Post reasonable, safe, and consistent speed limits on intersection THROUGH GEOMETRIC approaches IMPROVEMENTS Where to use - Signalized intersections with a high frequency of crashes attributed to Key to the Brochure drivers who intentionally disobey posted approach speed limits. B1 – Provide/improve turn lane l Keywords: Speed, speed management Costs: channelization Costs will also vary considerably and are affected by local conditions. Costs are ranked Where to use - Signalized intersections as: low, moderate, moderate to high, and high. The scale is meant to reflect costs with a high frequency of rear-end collisions relative to the other strategies described in the category (signalized or unsignalized). resulting
Recommended publications
  • Proofs with Perpendicular Lines

    Proofs with Perpendicular Lines

    3.4 Proofs with Perpendicular Lines EEssentialssential QQuestionuestion What conjectures can you make about perpendicular lines? Writing Conjectures Work with a partner. Fold a piece of paper D in half twice. Label points on the two creases, as shown. a. Write a conjecture about AB— and CD — . Justify your conjecture. b. Write a conjecture about AO— and OB — . AOB Justify your conjecture. C Exploring a Segment Bisector Work with a partner. Fold and crease a piece A of paper, as shown. Label the ends of the crease as A and B. a. Fold the paper again so that point A coincides with point B. Crease the paper on that fold. b. Unfold the paper and examine the four angles formed by the two creases. What can you conclude about the four angles? B Writing a Conjecture CONSTRUCTING Work with a partner. VIABLE a. Draw AB — , as shown. A ARGUMENTS b. Draw an arc with center A on each To be prof cient in math, side of AB — . Using the same compass you need to make setting, draw an arc with center B conjectures and build a on each side of AB— . Label the C O D logical progression of intersections of the arcs C and D. statements to explore the c. Draw CD — . Label its intersection truth of your conjectures. — with AB as O. Write a conjecture B about the resulting diagram. Justify your conjecture. CCommunicateommunicate YourYour AnswerAnswer 4. What conjectures can you make about perpendicular lines? 5. In Exploration 3, f nd AO and OB when AB = 4 units.
  • Traffic Calming Fact Sheets May 2018 Update Speed Table/Raised Crosswalks

    Traffic Calming Fact Sheets May 2018 Update Speed Table/Raised Crosswalks

    Traffic Calming Fact Sheets May 2018 Update Speed Table/Raised Crosswalks Description: • Long, raised speed humps with a flat section in the middle and ramps on the ends; sometimes constructed with brick or other textured materials on the flat section • If placed at a pedestrian crossing, it is referred to as a raised crosswalk • If placed only in one direction on a road, it is called an offset speed table Applications: • Appropriate for local and collector streets; mid-block or at intersections, with/without crosswalks • Can be used on a one-lane one-way or two-lane two-way street • Not appropriate for roads with 85th percentile speeds of 45 mph or more • Typically long enough for the entire wheelbase of a passenger car to rest on top or within limits of ramps • Work well in combination with textured crosswalks, curb extensions, and curb radius reductions • Can be applied both with and without sidewalks or dedicated bicycle facilities • Typically installed along closed-section roads (i.e. curb and gutter) but feasible on open section (Source: Google Maps, Boulder, Colorado) (Source: Delaware Department of Transportation) ITE/FHWA Traffic Calming EPrimer: https://safety.fhwa.dot.gov/speedmgt/traffic_calm.cfm Design/Installation Issues: • ITE recommended practice – “Guidelines for the Design and Application of Speed Humps” • Most common height is between 3 and 4 inches (reported as high as 6 inches) • Ramps are typically 6 feet long (reported up to 10 feet long) and are either parabolic or linear • Careful design is needed for drainage
  • Driver Understanding of the Flashing Yellow Arrow and Dynamic No Turn on Red Sign for Right Turn Applications

    Driver Understanding of the Flashing Yellow Arrow and Dynamic No Turn on Red Sign for Right Turn Applications

    University of Massachusetts Amherst ScholarWorks@UMass Amherst Masters Theses Dissertations and Theses July 2018 Driver Understanding of the Flashing Yellow Arrow and Dynamic No Turn on Red Sign for Right Turn Applications Elizabeth Casola University of Massachusetts Amherst Follow this and additional works at: https://scholarworks.umass.edu/masters_theses_2 Part of the Transportation Engineering Commons Recommended Citation Casola, Elizabeth, "Driver Understanding of the Flashing Yellow Arrow and Dynamic No Turn on Red Sign for Right Turn Applications" (2018). Masters Theses. 631. https://doi.org/10.7275/11923057 https://scholarworks.umass.edu/masters_theses_2/631 This Open Access Thesis is brought to you for free and open access by the Dissertations and Theses at ScholarWorks@UMass Amherst. It has been accepted for inclusion in Masters Theses by an authorized administrator of ScholarWorks@UMass Amherst. For more information, please contact [email protected]. DRIVER UNDERSTANDING OF THE FLASHING YELLOW ARROW AND DYNAMIC NO TURN ON RED SIGN FOR RIGHT TURN APPLICATIONS A Thesis Presented by ELIZABETH CASOLA Submitted to the Graduate School of the University of Massachusetts Amherst in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE IN CIVIL ENGINEERING May 2018 Civil Engineering DRIVER UNDERSTANDING OF THE FLASHING YELLOW ARROW AND DYNAMIC NO TURN ON RED SIGN FOR RIGHT TURN APPLICATIONS A Thesis Presented by ELIZABETH CASOLA Approved as to style and content by: ____________________________ Michael A. Knodler Jr., Chair ____________________________ Eleni Christofa, Member ____________________________ Cole Fitzpatrick, Member ____________________________________ Richard N. Palmer, Department Head Civil and Environmental Engineering Department ABSTRACT DRIVER UNDERSTANDING OF THE FLASHING YELLOW ARROW AND DYNAMIC NO TURN ON RED SIGN FOR RIGHT TURN APPLICATIONS MAY 2018 ELIZABETH CASOLA, B.S., UNIVERSITY OF MASSACHUSETTS AMHERST M.S.C.E., UNIVERSITY OF MASSACHUSETTS AMHERST Directed by: Michael A.
  • Some Intersection Theorems for Ordered Sets and Graphs

    Some Intersection Theorems for Ordered Sets and Graphs

    IOURNAL OF COMBINATORIAL THEORY, Series A 43, 23-37 (1986) Some Intersection Theorems for Ordered Sets and Graphs F. R. K. CHUNG* AND R. L. GRAHAM AT&T Bell Laboratories, Murray Hill, New Jersey 07974 and *Bell Communications Research, Morristown, New Jersey P. FRANKL C.N.R.S., Paris, France AND J. B. SHEARER' Universify of California, Berkeley, California Communicated by the Managing Editors Received May 22, 1984 A classical topic in combinatorics is the study of problems of the following type: What are the maximum families F of subsets of a finite set with the property that the intersection of any two sets in the family satisfies some specified condition? Typical restrictions on the intersections F n F of any F and F’ in F are: (i) FnF’# 0, where all FEF have k elements (Erdos, Ko, and Rado (1961)). (ii) IFn F’I > j (Katona (1964)). In this paper, we consider the following general question: For a given family B of subsets of [n] = { 1, 2,..., n}, what is the largest family F of subsets of [n] satsifying F,F’EF-FnFzB for some BE B. Of particular interest are those B for which the maximum families consist of so- called “kernel systems,” i.e., the family of all supersets of some fixed set in B. For example, we show that the set of all (cyclic) translates of a block of consecutive integers in [n] is such a family. It turns out rather unexpectedly that many of the results we obtain here depend strongly on properties of the well-known entropy function (from information theory).
  • Rural Expressway Intersection Synthesis of Practice and Crash Analysis

    Rural Expressway Intersection Synthesis of Practice and Crash Analysis

    RURAL EXPRESSWAY INTERSECTION SYNTHESIS OF PRACTICE AND CRASH ANALYSIS Sponsored by the Iowa Department of Transportation (CTRE Project 03-157) Final Report October 2004 Disclaimer Notice The opinions, fi ndings, and conclusions expressed in this publication are those of the authors and not necessarily those of the Iowa Department of Transportation. The sponsor(s) assume no liability for the contents or use of the information contained in this document. This report does not constitute a standard, specifi cation, or regulation. The sponsor(s) do not endorse products or manufacturers. About CTRE/ISU The mission of the Center for Transportation Research and Education (CTRE) at Iowa State Uni- versity is to develop and implement innovative methods, materials, and technologies for improv- ing transportation effi ciency, safety, and reliability while improving the learning environment of students, faculty, and staff in transportation-related fi elds. Technical Report Documentation Page 1. Report No. 2. Government Accession No. 3. Recipient’s Catalog No. CTRE Project 03-157 4. Title and Subtitle 5. Report Date Rural Expressway Intersection Synthesis of Practice and Crash Analysis October 2004 6. Performing Organization Code 7. Author(s) 8. Performing Organization Report No. T. H. Maze, Neal R. Hawkins, and Garrett Burchett 9. Performing Organization Name and Address 10. Work Unit No. (TRAIS) Center for Transportation Research and Education Iowa State University 11. Contract or Grant No. 2901 South Loop Drive, Suite 3100 Ames, IA 50010-8634 12. Sponsoring Organization Name and Address 13. Type of Report and Period Covered Iowa Department of Transportation Final Report 800 Lincoln Way 14. Sponsoring Agency Code Ames, IA 50010 15.
  • Complete Intersection Dimension

    Complete Intersection Dimension

    PUBLICATIONS MATHÉMATIQUES DE L’I.H.É.S. LUCHEZAR L. AVRAMOV VESSELIN N. GASHAROV IRENA V. PEEVA Complete intersection dimension Publications mathématiques de l’I.H.É.S., tome 86 (1997), p. 67-114 <http://www.numdam.org/item?id=PMIHES_1997__86__67_0> © Publications mathématiques de l’I.H.É.S., 1997, tous droits réservés. L’accès aux archives de la revue « Publications mathématiques de l’I.H.É.S. » (http:// www.ihes.fr/IHES/Publications/Publications.html) implique l’accord avec les conditions géné- rales d’utilisation (http://www.numdam.org/conditions). Toute utilisation commerciale ou im- pression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fichier doit contenir la présente mention de copyright. Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques http://www.numdam.org/ COMPLETE INTERSECTION DIMENSION by LUGHEZAR L. AVRAMOV, VESSELIN N. GASHAROV, and IRENA V. PEEVA (1) Abstract. A new homological invariant is introduced for a finite module over a commutative noetherian ring: its CI-dimension. In the local case, sharp quantitative and structural data are obtained for modules of finite CI- dimension, providing the first class of modules of (possibly) infinite projective dimension with a rich structure theory of free resolutions. CONTENTS Introduction ................................................................................ 67 1. Homological dimensions ................................................................... 70 2. Quantum regular sequences ..............................................................
  • DMV Driver Manual

    DMV Driver Manual

    New Hampshire Driver Manual i 6WDWHRI1HZ+DPSVKLUH DEPARTMENT OF SAFETY DIVISION OF MOTOR VEHICLES MESSAGE FROM THE DIVISION OF MOTOR VEHICLES Driving a motor vehicle on New Hampshire roadways is a privilege and as motorists, we all share the responsibility for safe roadways. Safe drivers and safe vehicles make for safe roadways and we are pleased to provide you with this driver manual to assist you in learning New Hampshire’s motor vehicle laws, rules of the road, and safe driving guidelines, so that you can begin your journey of becoming a safe driver. The information in this manual will not only help you navigate through the process of obtaining a New Hampshire driver license, but it will highlight safe driving tips and techniques that can help prevent accidents and may even save a life. One of your many responsibilities as a driver will include being familiar with the New Hampshire motor vehicle laws. This manual includes a review of the laws, rules and regulations that directly or indirectly affect you as the operator of a motor vehicle. Driving is a task that requires your full attention. As a New Hampshire driver, you should be prepared for changes in the weather and road conditions, which can be a challenge even for an experienced driver. This manual reviews driving emergencies and actions that the driver may take in order to avoid a major collision. No one knows when an emergency situation will arise and your ability to react to a situation depends on your alertness. Many factors, such as impaired vision, fatigue, alcohol or drugs will impact your ability to drive safely.
  • Making Streets Safe

    Making Streets Safe

    About WalkBoston WalkBoston plays an important role ensuring walker- CHICANE TREES BIKE friendly/safe designs and has an impressive record LANES of getting cities, towns, state agencies, developers, RAISED institutions, and elected officials to provide for the CROSSWALK needs of walkers. Every additional member helps our message be heard. Join online at walkboston.org. We work to transform communities into more walkable CURB places and reintroduce people to walking as a con- EXTENSION venient, healthy and low-cost transportation choice. People who depend on walking most: lower income, elders, children, people with disabilities, and transit PARKED users especially benefit from our advocacy. CARS SPEED How we can help you CUSHION • Advise on walking improvements for your community. MIDBLOCK CROSSWALK • Provide guidance, moral support, technical assistance. making • Give a variety of presentations on pedestrian design and advocacy. Speed Kills: Small-scale fixes go a long way to slow traffic • Help set up advocacy groups and strengthen them. • Demonstrate how these techniques are working streets The human costs and economic consequences of The tools can be small in scale, relatively inexpensive, across Massachusetts and elsewhere. speed-related crashes are immense. In 2007, about and are easily tested and evaluated. Streets can be 31 percent of all fatal crashes were speeding-related, made safer by putting them on a “road diet,” reducing safe resulting in 13,420 fatalities. In Massachusetts, 15 to speeds and enhancing pedestrian safety. Techniques Thanks to our supporters 20 percent of all road fatality victims are pedestrians. include signage, pavement devices and paint. Physically Nationwide, the economic cost to society of speed- or visually narrowing a standard width lane by 1 foot Striders ing-related crashes is estimated to be $40.4 billion slows cars by 7 miles per hour.
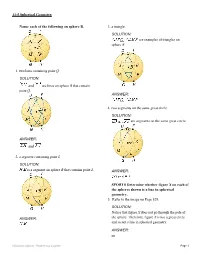
  • And Are Lines on Sphere B That Contain Point Q

    And Are Lines on Sphere B That Contain Point Q

    11-5 Spherical Geometry Name each of the following on sphere B. 3. a triangle SOLUTION: are examples of triangles on sphere B. 1. two lines containing point Q SOLUTION: and are lines on sphere B that contain point Q. ANSWER: 4. two segments on the same great circle SOLUTION: are segments on the same great circle. ANSWER: and 2. a segment containing point L SOLUTION: is a segment on sphere B that contains point L. ANSWER: SPORTS Determine whether figure X on each of the spheres shown is a line in spherical geometry. 5. Refer to the image on Page 829. SOLUTION: Notice that figure X does not go through the pole of ANSWER: the sphere. Therefore, figure X is not a great circle and so not a line in spherical geometry. ANSWER: no eSolutions Manual - Powered by Cognero Page 1 11-5 Spherical Geometry 6. Refer to the image on Page 829. 8. Perpendicular lines intersect at one point. SOLUTION: SOLUTION: Notice that the figure X passes through the center of Perpendicular great circles intersect at two points. the ball and is a great circle, so it is a line in spherical geometry. ANSWER: yes ANSWER: PERSEVERANC Determine whether the Perpendicular great circles intersect at two points. following postulate or property of plane Euclidean geometry has a corresponding Name two lines containing point M, a segment statement in spherical geometry. If so, write the containing point S, and a triangle in each of the corresponding statement. If not, explain your following spheres. reasoning. 7. The points on any line or line segment can be put into one-to-one correspondence with real numbers.
  • Chapter 5 Safety

    Chapter 5 Safety

    5 Safety 5.1 Introduction 103 5.2 Conflicts 104 5.2.1 Vehicle conflicts 105 5.2.2 Pedestrian conflicts 108 5.2.3 Bicycle conflicts 110 5.3 Crash Statistics 111 5.3.1 Comparisons to previous intersection treatment 111 5.3.2 Collision types 113 5.3.3 Pedestrians 117 5.3.4 Bicyclists 120 5.4 Crash Prediction Models 122 5.5 References 125 Exhibit 5-1. Vehicle conflict points for “T” Intersections with single-lane approaches. 105 Exhibit 5-2. Vehicle conflict point comparison for intersections with single-lane approaches. 106 Exhibit 5-3. Improper lane-use conflicts in double-lane roundabouts. 107 Exhibit 5-4. Improper turn conflicts in double-lane roundabouts. 108 Exhibit 5-5. Vehicle-pedestrian conflicts at signalized intersections. 109 Exhibit 5-6. Vehicle-pedestrian conflicts at single-lane roundabouts. 109 Exhibit 5-7. Bicycle conflicts at conventional intersections (showing two left-turn options). 110 Exhibit 5-8. Bicycle conflicts at roundabouts. 111 Exhibit 5-9. Average annual crash frequencies at 11 U.S. intersections converted to roundabouts. 112 Exhibit 5-10. Mean crash reductions in various countries. 112 Exhibit 5-11. Reported proportions of major crash types at roundabouts. 113 Exhibit 5-12. Comparison of collision types at roundabouts. 114 Exhibit 5-13. Graphical depiction of collision types at roundabouts. 115 Exhibit 5-14. Crash percentage per type of user for urban roundabouts in 15 towns in western France. 116 Exhibit 5-15. British crash rates for pedestrians at roundabouts and signalized intersections. 117 Exhibit 5-16. Percentage reduction in the number of crashes by mode at 181 converted Dutch roundabouts.
  • Chapter Four Pedestrian Facility Recommendations

    Chapter Four Pedestrian Facility Recommendations

    CHAPTER FOUR PEDESTRIAN FACILITY RECOMMENDATIONS This chapter recommends two types of Recommendations included in this chapter are infrastructure improvements: planning-level design concepts. This means that the recommendations are guided by the »» Design concepts for six example plan goals and informed by existing conditions, locations; and prioritized missing best practices, and opportunities identified sidewalk links in the City. The during field work. Additional engineering example location recommendations analysis and field work is needed before show how a mix of treatments can proceeding with project implementation. improve the pedestrian network in a defined area. Recommended Example Locations treatments include sidewalks, pedestrian crossing facilities, and bus Six locations were identified for field work in stop improvements. order to develop conceptual recommendations »» A prioritized list of sidewalk projects. to improve pedestrian safety and comfort. Sidewalk projects are scored and These “example locations” were identified from ranked using the new method several sources, including the demand and recommended in Chapter 3. needs analysis, public input, and input from the City’s technical team. Appendix C provides 76 DECEMBER 2012 sample comments from CommunityWalk of the design concepts are described in around each example location. Chapter 3, Best Practices, Design Standards and Sidewalks. Overall, recommended design The example locations are typical of pedestrian concepts are intended to achieve one or more of conditions in many areas of the City. Thus, the following objectives: these design concepts recommended can be applied elsewhere in the City. The example locations are not in any priority order. Many Ensure ADA compliance. Ensure sufficient crossing time. All sidewalks and intersection features meet Adjust signal timing to ensure pedestrians have at standards set by PROWAAG, NCDOT and the City of least 3.5 feet per second to cross the street.
  • Intersection of Convex Objects in Two and Three Dimensions

    Intersection of Convex Objects in Two and Three Dimensions

    Intersection of Convex Objects in Two and Three Dimensions B. CHAZELLE Yale University, New Haven, Connecticut AND D. P. DOBKIN Princeton University, Princeton, New Jersey Abstract. One of the basic geometric operations involves determining whether a pair of convex objects intersect. This problem is well understood in a model of computation in which the objects are given as input and their intersection is returned as output. For many applications, however, it may be assumed that the objects already exist within the computer and that the only output desired is a single piece of data giving a common point if the objects intersect or reporting no intersection if they are disjoint. For this problem, none of the previous lower bounds are valid and algorithms are proposed requiring sublinear time for their solution in two and three dimensions. Categories and Subject Descriptors: E.l [Data]: Data Structures; F.2.2 [Analysis of Algorithms]: Nonnumerical Algorithms and Problems General Terms: Algorithms, Theory, Verification Additional Key Words and Phrases: Convex sets, Fibonacci search, Intersection 1. Introduction This paper describes fast algorithms for testing the predicate, Do convex objects P and Q intersect? where an object is taken to be a line or a polygon in two dimensions or a plane or a polyhedron in three dimensions. The related problem Given convex objects P and Q, compute their intersection has been well studied, resulting in linear lower bounds and linear or quasi-linear upper bounds [2, 4, 11, 15-171. Lower bounds for this problem use arguments This research was supported in part by the National Science Foundation under grants MCS 79-03428, MCS 81-14207, MCS 83-03925, and MCS 83-03926, and by the Defense Advanced Project Agency under contract F33615-78-C-1551, monitored by the Air Force Offtce of Scientific Research.