Morphodynamic Modelling of a Complex Estuarine System
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

U3A News August 2021
Newsletter August 2021 he has become a Devon historian, Our next Members Meeting speaker, author and a group leader for Monday 16th August at 2pm the Devon Family History Society. He has recently published a book entitled 'History Dawlish Town Council Offices, Tours of Torquay' and is soon to publish the Manor House another about the boatmen of Babbacombe Bay. Speaker: Phil Badcott Folklore of bygone Devon – anecdotes from the nineteenth century Our get together last month was well attended. We had a few teething problems with it being the first time we’d held such a meeting in the Manor House, but on the whole it was light, (sometimes a bit too light to see the screen), airy and had plenty of room. Lynne McVernon gave an interesting talk about her time in theatre spanning over 25 years from sweeping the stage to directing and writing. From being a Butlins Rep to working in The National Theatre. This month we have Phil Badcott coming to talk to us. His very interesting title, Folklore of bygone Devon – anecdotes from the You are warmly invited to meet nineteenth century, is a light hearted together again and enjoy a very social look at the folklore of Devon. He will afternoon. Save the date! dip into the accounts of several of our P.S. If you have any suitable raffle 19th century Devonian writers and find out about what our ancestors really prizes, please bring them along to the believed about sneezing, cures for meeting and donate them to our raffle. ailments, counteracting evil and many other Devon customs. -

Babbacombe-Brochure-Oct2020.Pdf
INDEPENDENT SEASIDE LIVING IN TORQUAY With Torquay being so desirable and sought- stunning sea views. A parking space is also after, we wanted to bring our fantastic offer available for each apartment. to the Devon coast. Renaissance is proud to present our beautiful development in Nearby Oddicombe Beach with its colourful Babbacombe, Torquay, part of our Cavendish beach huts, shops and cafés, has everything Collection. With stunning views over the you need for an idyllic afternoon out. The cliffs and a 10 minute walk to the beach, this beach is a Blue flag award winner, boasting is the perfect location to live beside such an beautiful clear water in an unspoiled, secluded incredible piece of coastline. arc. Walk down the slope from Babbacombe Downs to the tranquil haven, and on the way Our development, built specifically for the over back up take the Babbacombe Cliff Railway. 55s, comprises nine spacious two bedroom These views are not to be missed. apartments. Most homes benefit from its private outdoor space, whether this is a private terrace on the ground floor or a balcony with ABOUT RENaissaNCE Renaissance was founded in the 1990s with We’re proud to present Sandbanks Road, where the aim of designing, building and managing you can enjoy independent living in a desirable, retirement developments that were simply stylish and comfortable environment, safe in better than the standard being built across the the knowledge that your home is secure. You country at the time. That ethos still resonates will also have the support of your Lifehost today. At Renaissance it is still, and will always should you need it – a very welcome assurance be, the personal touch that sets us apart. -

The Perfect Weekendin
tHe PerfeCt Weekend 2 SaTurday afTernoon new seRies T he perfecT weekend in... TOR BAY 1 SaTurday morning The route: Brixham, Scabbacombe, Fishcombe, Torquay, Babbacombe Bay Known as the English Riviera, the coast around Tor Bay does feel to skirt the dramatic sheer scars of Berry Head. You’ll see the tiny like the Côte d’Azur on a warm summer day. Glitzy hotels and dots of holidaymakers on the summit, enjoying superb views apartments are softened by pines in the style of Villefranche or across Tor Bay, south towards Start Bay and north-east across Lyme Beaulieu-sur-Mer. The beaches at Paignton and Goodrington have Bay, where the Dorset coast curves out towards Portland Bill. Watch Brixham’s Stop for a leisurely bluffs of red sandstone with echoes of St Raphaël. Cruising south past Cod Rock you may be tempted by St Mary’s working harbour come lunch at the tranquil But on the south side of the bay, Brixham is the West Country golden beach cordoned by swimming buoys, but it’s best to follow to life around you Scabbacombe Bay fishing port it has always been. Close-packed houses stack up from the coast another couple of miles down to a smaller cove just enjoy a peaceful To Dawlish 3 SaTurday evening night at anchor in the water’s edge and you can imagine the narrow streets and tread- north of Scabbacombe Head. Fishcombe Cove Teignmouth worn steps winding between them. Friendly Brixham Marina is just the place to start a perfect boating weekend in Tor Bay. -

Seaview Cottages Babbacombe Beach, South Devon
Seaview Cottages Babbacombe Beach, South Devon TQ1 Seven Newly built and Beautifully Finished Cottages, with Unparalleled far reaching Sea views across Babbacombe Bay and the Jurassic Coast. View from all of the cottages Situation & Amenities Built to an exceptionally High standard, these characterful Cottages have been created by the Renowned Hotelier Peter de Savary , who is also the Owner of the Legendary Cary Arms Inn and Spa on the Beach below. These Cottages are built on Three floors, finished in local red sandstone and colour washed render under a slate/tile roofs. The Ground floor comprises of the entrance hall, Double bedroom/ 2nd reception room with ensuite shower room and a utility/boot/ laundry room. The entire First floor is devoted to a large living/ dining room incorporating a fully fitted Kitchen. All Three floors have breath-taking views particularly from the Balcony and Private Terraces which include a Hydrotherapy Hot Tub. The top floor provides the Master Bedroom and a further Double Guest Bedroom both with ensuite facilities. Each property has private parking and they share a common refuse storage area and a Wild Garden area for the benefit of Dogs and Cats. These extraordinary and most unusual Cottages have a private electric gated entrance with camera security. Nestled into the Hillside, Seaview Cottages are a masterclass of creativity providing the Ultimate Escape to Seaside living in a Location Second to None! For wider requirements Torquay town centre (2.5 miles) and Exeter city centre (23.5 miles) are also within easy driving distance. Access to local transport links are excellent. -
Evaluation Report of the Lyme Bay 2 Dredged Material Disposal Site
Evaluation Report of the: Lyme Bay 2 Dredged Material Disposal Site Characterisation Report (PO050) 28 August 2020 Draft Prepared by Luella Williamson Date 03/06/2020 Draft Checked by Adam Chumbley Date 06/07/2020 (HEO) Draft Amended by Luella Williamson Date 15/07/2020 Draft Checked by Chris Turner Date 24/07/2020 (SEO) Draft Checked by (G6) Shaun Nicholson Date 10/08/2020 Draft Amended by Luella Williamson Date 25/08/2020 Final Version Signed Shaun Nicholson Date 28/08/2020 off OR Rejected by Page 1 of 18 Contents 1. Executive Summary .............................................................................................. 3 2. The Proposal ......................................................................................................... 4 2.1 Background ..................................................................................................... 4 2.2 Site Characterisation ....................................................................................... 4 2.3 Scenario 1 ....................................................................................................... 5 3. Legislative and Policy Framework ......................................................................... 5 4. Site Selection Report ............................................................................................ 6 5. Site Characterisation Report ................................................................................. 7 6. Consultation Exercise .......................................................................................... -

Babbacombe Bay House 33-35 Babbacombe Downs Road | Babbacombe | Torquay | TQ1 3LN Babbacombe Bay House 33-35 Babbacombe Downs Road | Babbacombe | Torquay | TQ1 3LN
Babbacombe Bay House 33-35 Babbacombe Downs Road | Babbacombe | Torquay | TQ1 3LN Babbacombe Bay House 33-35 Babbacombe Downs Road | Babbacombe | Torquay | TQ1 3LN Uninterrupted views over the picturesque Babbacombe Downs into Lyme Bay are just one of the attributes of this FINE COASTAL RESIDENCE AND EXCEPTIONAL INVESTMENT OPPORTUNITY. The property comprises FOUR QUALITY HOLIDAY FLATS, additional rear FLAT let to an established tenant, COMMERCIAL UNIT leased to a popular cafe/restaurant and EQUISITE OWNERS ACCOMMODATION arranged over three levels topped off with a ROOF TERRACE commanding panoramic views. | 2 THE LOWER REAR FLAT Accessed from the rear off Portland Road. Generous studio design with large open plan principal living space. Currently let on an assured shorthold THE OWNERS ACCOMMODATION tenancy agreement to a good tenant wishing to remain. | Babbacombe Bay House THE HOLIDAY APARTMENTS A private entrance off Portland Road keeps the holiday flats separate from A private approach from Babbacombe Downs Road leads the rest of the building, with connecting door at entrance level from the to a storm porch and welcoming reception hall with secure owners accommodation. A spacious reception hall and attractive turned connecting door accessing the adjoining holiday flats. staircase lead to the four apartments, named after local landmarks and The SITTING ROOM features a raised bay from where the places. ‘THE DOWNS SUITE’, a seaward facing studio flat opening to a stunning views are enjoyed. The KITCHEN/DINING ROOM private balcony with separate kitchen and shower room. ‘ODDICOMBE SUITE’, a south westerly facing rear studio flat with kitchen opening is beautifully appointed with high gloss units topped off to a balcony and bathroom. -

Top 10 6 5 Uk Desination for the Past Three Years
TOP 10 6 5 UK DESINATION FOR THE PAST THREE YEARS ABBEY LAWN HOTEL BELGRAVE SANDS & SPA CORBYN HEAD HOTEL DEVONSHIRE HOTEL Group Rates: Group Rates: Group Rates: Group Rates: Prices on request *VSQTTTR From £45.00 RMKLXW(& &JVSQTT The Abbey Lawn Hotel is a traditional family hotel in the Belgrave Sands & Spa is a newly renovated 50-bedroom hotel, Corbyn Head Hotel undoubtedly has one of the most enviable Devonshire Hotel is a beautiful 1900s building overlooking the grounds of the former Torre Abbey. The standard of comfort is EPPVSSQWEVIWX]PMWLP]½RMWLIH[MXLSRP]XLILMKLIWXUYEPMX] locations in Torquay; just a stone’s throw from the beaches and a WXYRRMRK8SV&E]MXMWWYVVSYRHIHF]¾S[IV½PPIHKEVHIRWERH exceptional throughout, with many bedrooms offering panoramic JYVRMWLMRKWFVERHRI[FEXLVSSQWGSQTPMQIRXEV][M½ERHE level walk to the Town Centre. just a 10-minute stroll to the popular Blue Flag-rated Meadfoot views of the bay. The hotel is a short distance from the KYIWXWIVZMGIWXIEQEZEMPEFPILSYVWEHE]XSLIPT]SY[MXL Most of the bedrooms have stunning sea views and many with &IEGLXLIEXXVEGXMZI[EXIVJVSRXERHFYWXPMRKXS[RGIRXVI promenade and town centre. The hotel boasts an indoor heated ]SYVIZIV]RIIH7XYRRMRKPSGEXMSR private balconies. Our heated outdoor pool is available in the summer (May to TSSPERHHERGI¾SSV 7ITX 2MKLXP]IRXIVXEMRQIRX Free coach parking Free coach parking Free coach parking Free coach parking Contact: Contact: Contact: Contact: Scarborough Road, Torquay 01983 861 111 &IPKVEZI6SEH8SVUYE] 01803 226 366 Torbay Road, Torquay 01803 213 611 Park -
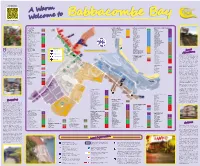
Babbacombe Bay
For even more local information A Warm SCAN HERE Welcome to Babbacombe Bay AUTO SERVICES 1 SPORTS & LEISURE HOTELS & ACCOMMODATION RESTAURANTS, CAFES & TAKEAWAYS St. Anne’s Garage 47 2 Babbacombe Corinthian Sailing Club 26 Seabury Hotel 51 Pizza Hut 10 3 Babbacombe Garage 3 Marisa Burgoyne School of Dance 9 Babbacombe Hall Hotel 50 Chinagarden 9 1 CTR Car Sales 3a 4 Torquay United AFC 14 Blue Conifer 1 Hoi Wang Chinese Takeaway 7 5 Torquay United Bowling Club 17 Norcliffe Hotel 3 The Usual Plaice 6 BANKS, FINANCIAL & LEGAL Boots and Laces 15 Sunningdale 4 Domino’s Pizza 36 6 MyDebtsSolved.com 27 Swim Torquay 16 Sefton Hotel 9 Hong Kong Kitchen 23 Adding & Calculating Bureau 22 7 2 One Vision One Fitness 6 The Morningside Hotel 8 Plainmoor Fish Bar 19a 3 R A Armitage & Associates 54 Divers Down 41 Oddicombe Hall Hotel 5 Crusty Loaf Café 18 4 Family Matters Solicitors 10a 5 8 6 Bay Cycles 23 Exmouth View Hotel 6 Green Chillies 19 7 9 8 TSB 32 10 Headland View 12 Cliff Railway Café 2 9 11 National Westminster Bank 38 10 12 Angels Tea Room 15 10a 13 28 Seabreeze 13 14 HSBC Bank 33 11 23 15 24a Babbacombe Bay Hotel 11 Babbacombe Beach Café 22 12 22a 16 22 45 Somerville & Savage (Allens Conveyancing) 32a 13 17 21 The Downs Hotel 14 Oddicombe Beach Café 24 14 18 20 Somerville & Savage Solicitors 52 19 24 15 19a Coombe Court Hotel 19 Hanbury’s Licensed Fish Restaurant 65 16 24 Peplows Accountants 52a 17 25 18 26 26 The Royal Hotel 10 Hanbury’s Fish Takeaway 65a 18a 27 Chudley & Co Accountants 43 18b Daisy's Tea Rooms 10 19 28 Cary Arms Hotel 21 Darby & Darby Solicitors 39 20 29 30a Hotel De La Mer 7 Middle Room Café 23 21 30 25 St Marychurch Post Office 41 22 Abigails Cafe 30 23 31 23 Ashley Rise Hotel 6 Barclays Bank 35 24 The Trecarn 7 Himalaya 24 21a 25 32 33 24a 26 Anchorage 10 Cary Park Café 20 abbacombe Bay has been attracting 27 BOOKMAKERS MAP SYMBOLS Aveland House 11 Mirch Masala 66 William Hill Organization 12 holiday visitors to the English Riviera 28 Babbacombe Palms Guest House 3 The Coffee Bean 35 William Hill Organization 4 30d for many years. -

Dear Guest, Welcome to the Cary Arms, I Hope That You Have an Enjoyable and Relaxing Stay with Us on Babbacombe Bay. Please Read
Dear Guest, Welcome to The Cary Arms, I hope that you have an enjoyable and relaxing stay with us on Babbacombe Bay. Please read this compendium for some useful information regarding your room, the hotel, and the surrounding area. If there are any areas we haven’t covered my team are on hand 24 hours a day to help you out with anything you may need. If during your stay there is absolutely anything you wish to discuss with me, please do not hesitate to do so by either asking for me on site or contacting me on my mobile number which is listed at the end of the compendium. I would also like to ask you a small favour; I think my team work very hard and do their best to look after you. If during your stay one (or more) of the team in particular does really impress you then please take the time to leave a Trip Advisor review mentioning their name so I can award them a cash bonus! Now, please sit back with a complimentary sloe gin and enjoy the view! Best Regards, David Adams General Manager Contacting Reception The Cary Arms is manned 24 hours a day with a full team available from 7am until 11pm and a night porter is also available for emergencies outside of these hours. If there is anything at all you need, from booking a table in the restaurant, ordering a taxi, advice on the local area, or maintenance issues to report please do not hesitate to contact reception either in person or by calling 01803 327110. -

Seascape Characterisation Around the English Coast (Marine Plan Areas 3 and 4 and Part of Area 6 Pilot Study)
Natural England Commissioned Report NECR106 Seascape Characterisation around the English Coast (Marine Plan Areas 3 and 4 and Part of Area 6 Pilot Study) First published 11 October 2012 www.naturalengland.org.uk Foreword Natural England commission a range of reports from external contractors to provide evidence and advice to assist us in delivering our duties. The views in this report are those of the authors and do not necessarily represent those of Natural England. Background Seascape, like landscape, reflects the connections between land and sea reflected relationship between people and place and the in the Marine and Coastal Access Act (2009) part it plays in forming the setting to our and the resultant marine spatial planning everyday lives. It is a product of the interaction system. of the natural and cultural components of our 3) Undertake a Seascape Character environment, and how they are understood and Assessment at a strategic scale for a defined experienced by people. area of the English coastline, so that a baseline of Seascape Character Areas is This work was commissioned to test and refine available to: the emerging methodology for assessing the character of seascapes and to: provide the context for more detailed Seascape Character Assessment work; and 1) Contribute to the aims of the European inform Marine Spatial Planning, and the Landscape Convention to promote landscape planning, design and management of protection, management and planning, and to developments - and a range of other projects - support European co-operation -

Livrables 2012
PROJET INTERREG IV A France-Manche- Angleterre CRESH LIVRABLES 2012 CRESH Progress Report/ RAPPORT d’avancement 2012 Task 2 In situ observations of natural substrata where spawning females attach their eggs Observation des supports naturels utilisés pour la ponte sur des sites pilotes Objective/Objectifs: In situ observation of natural substratum where spawning females attach their eggs (in both English and French coastal waters). Analysis of environmental variability of eggs and hatchlings habitats (diving observations and experimental fishing). Observation des supports naturels utilisés pour la ponte sur des sites pilotes (côtes anglaises et françaises). Etude de la variabilité des substrats et des conditions environnementales entourant les œufs et les juvéniles (observations en plongée et pêches expérimentales). Work progress until 30/07/2012 Etat d’avancée des travaux au 31 juillet 2012 Task 2 database available in the DVD included in claim 4 parcel La base de donnée de la tâche 2 est disponible sur le DVD inclus dans le colis de la remontée de dépenses n°4 I. 2012 Task Results Summary / Résumé des résultats obtenus en 2012 Subtidal observations of natural egg laying structures and habitats were undertaken within two seagrass beds at the study site of Torbay on the UK coast. These observations were completed as part of a time series which was carried out from 2010 to 2012. Surveys were conducted in May, June and July using a 100 m2 line belt transect. The results of this research showed that densities of eggs within these two areas was significantly lower than in 2011 and that this may be the result of increased natural disturbance (e.g. -
Study of Wild Hippocampus Hippocampus in Torbay, Devon
Diver study of wild Short Snouted Seahorses (Hippocampus hippocampus) in Torbay, Devon. Neil Garrick-Maidment (1), John Newman (2) (1)The Seahorse Trust, Escot Park, Ottery St Mary, Honiton, Devon EX11 1LU (2) 71 Chudleigh Road, Kingsteington, Newton abbot. Devon TQ12 3JS The British Isles are home to 2 species of Seahorse, Hippocampus guttulatus (The Spiny Seahorse) and Hippocampus hippocampus (The Short Snouted Seahorse); the British Seahorse Survey was set up in 1994 by The Seahorse Trust to study both of the species in the wild and we have now accrued a huge amount of data about them but it is seldom we get a chance to study individuals for any length of time in the wild. So the opportunity to study a pair of Hippocampus hippocampus in Torbay, Devon for 3 months was invaluable to gather much needed data on their ecology and behaviour in the wild. John Newman (the Seahorse Trust) studied a pair of Short Snouted Seahorses at Babbacombe in Torbay in Devon and spent over 300 hours watching behaviour and taking photographs. Corresponding author: N. Garrick-Maidment Email: [email protected] Keywords: Hippocampus guttulatus, H.hippocampus, Zostera marina, home range, courtship, reproduction, SCUBA, British Seahorse Survey, Wildlife and Countryside Act, Introduction The Seahorse Trust runs the British Seahorse Survey (BSS) and runs the National Seahorse Database (NSD) at its headquarters at Escot Park nr Ottery St Mary in East Devon and has focused on both British species of seahorses in the UK. Through their work they have made numerous discoveries about both British species of seahorses and submitted and got both species protected under the Wildlife and Countryside Act (1981).