ORIGINAL ARTICLES the Probability of Karun River Environmental Pollution Due to Seismic Response of Masjed Soleyman
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Karim Dahimi Place of Birth
Page 1 of 15 Witness Statement of Karim Dahimi Witness Statement of Karim Dahimi Name: Karim Dahimi Place of Birth: Ahvaz, Iran Date of Birth: September 23, 1971 Occupation: Teacher Interviewing Organization: Iran Human Rights Documentation Center (IHRDC) Date of Interview: September 25, 2012 Interviewer: IHRDC Staff This statement was prepared pursuant to an interview with Karim Dahimi. It was approved by Karim Dahimi on September 25, 2013. There are 66 paragraphs in the statement. The views and opinions of the witness expressed herein do not necessarily reflect those of the Iran Human Rights Documentation Center. Page 2 of 15 Witness Statement of Karim Dahimi Statement Introduction 1. My name is Karim Dahimi. I was born in October, 1971. I was a schoolteacher and a resident of the Kuh Alavi neighborhood of Ahvaz. I am married and have three children. Initial Activities 2. My [cultural] activities began in 1989. I received my high school diploma in 1989-90 and from 1991-93, I was a university student majoring in education. Our activities at the time were limited to the distribution of statements and having connections with other groups in Mohammareh, Fallahiyeh1, Shush and other cities to hold cultural gatherings such as poetry readings. We did not engage in any other activities. Nevertheless, my file [with the security services] listed these activities as "intelligence-gathering" and "actions against national security." There was only one thing [that I did] that could have been considered very dangerous from the point of view of the Islamic Republic; my actions in relation to the sugarcane project. -

Possibilities of Restoring the Iraqi Marshes Known As the Garden of Eden
Water and Climate Change in the MENA-Region Adaptation, Mitigation,and Best Practices International Conference April 28-29, 2011 in Berlin, Germany POSSIBILITIES OF RESTORING THE IRAQI MARSHES KNOWN AS THE GARDEN OF EDEN N. Al-Ansari and S. Knutsson Dept. Civil, Mining and Environmental Engineering, Lulea University, Sweden Abstract The Iraqi marsh lands, which are known as the Garden of Eden, cover an area about 15000- 20000 sq. km in the lower part of the Mesopotamian basin where the Tigris and Euphrates Rivers flow. The marshes lie on a gently sloping plan which causes the two rivers to meander and split in branches forming the marshes and lakes. The marshes had developed after series of transgression and regression of the Gulf sea water. The marshes lie on the thick fluvial sediments carried by the rivers in the area. The area had played a prominent part in the history of man kind and was inhabited since the dawn of civilization by the Summarian more than 6000 BP. The area was considered among the largest wetlands in the world and the greatest in west Asia where it supports a diverse range of flora and fauna and human population of more than 500000 persons and is a major stopping point for migratory birds. The area was inhabited since the dawn of civilization by the Sumerians about 6000 years BP. It had been estimated that 60% of the fish consumed in Iraq comes from the marshes. In addition oil reserves had been discovered in and near the marshlands. The climate of the area is considered continental to subtropical. -

Future Strategies for Promoting Tourism and Petroleum Heritage in Khuzestan Province, Iran
Future strategies for promoting tourism and petroleum heritage in Khuzestan Province, Iran Sahar Amirkhani, Neda Torabi Farsani and Homa Moazzen Jamshidi Abstract Sahar Amirkhani and Purpose – Industrial tourism not only strives to preserve industrial heritage, but can also be a strategy for being Neda Torabi Farsani are both familiar with the history of industry and attracting tourists to new destinations. This paper examines the issue of based at the Department of promoting petroleum industrial tourism in the case of Khuzestan, Iran. The research aims at determining Museum and Tourism, Art appropriate strategies for promoting petroleum industrial tourism. University of Isfahan, – Design/methodology/approach The data were analysed through a strengths, weaknesses, opportunities, Isfahan, Iran. and threats (SWOT) model. Homa Moazzen Jamshidi is Findings – The results revealed the competitive strategy as the best. Lastly, strategies such as: concentric based at the Department of diversification, joint venture strategy, conglomerate diversification and horizontal diversification were proposed Economics and Arts as key solutions. The results support the view that establishing an exploratory ecomuseum in the territory of Entrepreneurship, Art Khuzestan Province can be a suitable concentric diversification strategy towards petroleum industrial sustainable tourism in the future. University of Isfahan, Originality/value – The main originality of this paper includes linking tourism with the petroleum (oil and natural Isfahan, Iran. gas) industry -

Iranian Cancer Researcher Detained Despite Valid Visa
Art & Culture July 13, 2017 3 This Day in History Iranian Cancer Researcher (July 13) Today is Thursday; 22nd of the Iranian month of Tir 1396 solar hijri; corresponding to 18th of the Islamic month of Shawwal 1438 lunar hijri; and July 13, 2017, of the Christian Gregorian Calendar. Detained Despite Valid Visa 1069 lunar years ago, on this day in 368 AH, the pleasure-seeking Ezz od- Dowla Daylami, son of Moiz od-Dowla the Buwaihid conqueror of Baghdad, to return to Iran around 9 p.m., was killed in battle with his cousin, Adhud od-Dowla, the son of Rukn od- Dowla, near the River Tigris after rebelling against the central authority of the despite having a valid work visa then Shiraz-based Buwaihid confederacy. Adhud od-Dowla, a few years later to join the Boston Children’s after the passing away of his father, became the senior-most Buwaihid Amir of Iraq and Fars, at a time when Baghdad was wracked by violence and instability. Hospital, according to the Boston He restored peace and patronized scholars such as the celebrated Shaikh Mufid, Globe. besides renovating the holy shrines in Najaf and Karbala. An observatory was It’s not clear as why Dehnavi built by him in Isfahan, and the dam known till this day as “Band-e Amir” was built on his orders between Shiraz and Istakhr. He dug the Haffar Canal joining and his family are being detained the Karun River to the Arvand Roud at the confluence of the Rivers Tigris and — but they’ll likely be deported Euphrates. -

The Foreign Service Journal, February 1960
40$.(&I872 100 86 PROOF PROOF its always a pleasure In the lighter, milder 86 Proof or in IOO Proof Bottled in Bond Every drop of the milder 86 Proof is original and genuine I. W. Harper bourbon — distilled and bottled at the same dist KENTUCKY KENTUCKY ST 1 as the famous IOO Proof Bottled in Bond. &AIGHT BOURBC* SI&AIGHT BOUSBOH WHISKEY WHISKEY H*»PtR DISTUUNG' F0UNDER”MEM8ER BOTH KENTUCKY STRAIGHT BOURBON WHISKEY HARPER DISTILLING COMPANY, LOUISVILLE, KENTUCKY STRICTLY frivolous but so vital that you order NOW! MEN’S Summer Jackets $22.90 Hand woven Indian Madras—no favorite of ours, guaranteed to “bleed” which means color runs, stains etc. Domestic Dacron-Cotton Madras which are utterly perfect. WASH’N’WEAR. TRAVIS, Linen-Dacron eggshell color “goes”-with-any color SLAX, wash’n’wear (woven for us exclusively and the world’s most demanded jacket-iron-wear. Immediate ordering VITAL). MEN’S TROPICAL-wash’n’wear One man . one product . one company stands pre-eminent in every field. Since the inception of this unique field there’s no doubt of whom it IS. Price $22.90 & $32.90 Eggshell, Vycron-E. Cotton Strictly frivolous; womens’ VICUNA, anybody? $149. Made solely for Manila, All colors, hand-made—excellent etc. Weightless. $32.90 device for inducing feminine euphoria. (Wash’n’wear in Ifi minutes—woven for you solely) MONGOLIAN CASHMERE $72.90 Chuang-Tzu quality, rare and precious Wash’N’Wear Men’s Slacks and never varying in quality. Another Please specify color wanted as swatching is nearly excellent feminine euphoria booster. -

Analysis of Geographical Accessibility to Rural Health Houses Using the Geospatial Information System, a Case Study: Khuzestan Province, South-West Iran
Acta Medica Mediterranea, 2015, 31: 1447 ANALYSIS OF GEOGRAPHICAL ACCESSIBILITY TO RURAL HEALTH HOUSES USING THE GEOSPATIAL INFORMATION SYSTEM, A CASE STUDY: KHUZESTAN PROVINCE, SOUTH-WEST IRAN FARAHNAZ SADOUGHI1, 2, JAVAD ZAREI1, ALI MOHAMMADI3, HOJAT HATAMINEJAD 4, SARA SAKIPOUR5 1Department of Health Information Management, School of Health Management and Information Science, Iran University of Medical Sciences, Tehran, I.R. Iran - 2Health Management and Economics Research Center, School of Health Management and Information Sciences, Iran University of Medical Sciences, Tehran, I.R. Iran - 3Assistant professor of Health Information Management, Department of Health Information Technology, Paramedical School, Kermanshah University of Medical Sciences, Kermanshah I.R. Iran - 4PhD candidate, Geography and Urban Planning, University of Tehran, Tehran - 5Office of Medical Record and Statistics, Vice-Chancellor for Treatment, Ahvaz Jundishapur University of Medical Sciences, Ahvaz, I.R. Iran ABSTRACT Background: The use of rural health houses is one of the important approaches for delivering health services but, inappro- priate infrastructures and limited resources make it difficult to design and implement plans to enhance and improve health services in rural areas. The aim of this study was to analyze the accessibility to rural health care services in the province of Khuzestan Materials and methods: This applied research was conducted in Khuzestan Province, south-west Iran with a cross-sectional approach in 2014. The population of the study was the villages and rural health houses. All the villages and rural health houses were included in the study without sampling. Descriptive data collected with a checklist from the Statistical Centre of Iran, IT Department of the Management Deputy of the Governor’s Office and Ahvaz Jundishapur and Dezful University of Medical Sciences and spatial data obtained from the national Cartographic Center. -

See the Document
IN THE NAME OF GOD IRAN NAMA RAILWAY TOURISM GUIDE OF IRAN List of Content Preamble ....................................................................... 6 History ............................................................................. 7 Tehran Station ................................................................ 8 Tehran - Mashhad Route .............................................. 12 IRAN NRAILWAYAMA TOURISM GUIDE OF IRAN Tehran - Jolfa Route ..................................................... 32 Collection and Edition: Public Relations (RAI) Tourism Content Collection: Abdollah Abbaszadeh Design and Graphics: Reza Hozzar Moghaddam Photos: Siamak Iman Pour, Benyamin Tehran - Bandarabbas Route 48 Khodadadi, Hatef Homaei, Saeed Mahmoodi Aznaveh, javad Najaf ...................................... Alizadeh, Caspian Makak, Ocean Zakarian, Davood Vakilzadeh, Arash Simaei, Abbas Jafari, Mohammadreza Baharnaz, Homayoun Amir yeganeh, Kianush Jafari Producer: Public Relations (RAI) Tehran - Goragn Route 64 Translation: Seyed Ebrahim Fazli Zenooz - ................................................ International Affairs Bureau (RAI) Address: Public Relations, Central Building of Railways, Africa Blvd., Argentina Sq., Tehran- Iran. www.rai.ir Tehran - Shiraz Route................................................... 80 First Edition January 2016 All rights reserved. Tehran - Khorramshahr Route .................................... 96 Tehran - Kerman Route .............................................114 Islamic Republic of Iran The Railways -

Novel Hydraulic Structures and Water Management in Iran: a Historical Perspective
Novel hydraulic structures and water management in Iran: A historical perspective Shahram Khora Sanizadeh Department of Water Resources Research, Water Research Institute������, Iran Summary. Iran is located in an arid, semi-arid region. Due to the unfavorable distribution of surface water, to fulfill water demands and fluctuation of yearly seasonal streams, Iranian people have tried to provide a better condition for utilization of water as a vital matter. This paper intends to acquaint the readers with some of the famous Iranian historical water monuments. Keywords. Historic – Water – Monuments – Iran – Qanat – Ab anbar – Dam. Structures hydrauliques et gestion de l’eau en Iran : une perspective historique Résumé. L’Iran est situé dans une région aride, semi-aride. La répartition défavorable des eaux de surface a conduit la population iranienne à créer de meilleures conditions d’utilisation d’une ressource aussi vitale que l’eau pour faire face à la demande et aux fluctuations des débits saisonniers annuels. Ce travail vise à faire connaître certains des monuments hydrauliques historiques parmi les plus fameux de l’Iran. Mots-clés. Historique – Eau – Monuments – Iran – Qanat – Ab anbar – Barrage. I - Introduction Iran is located in an arid, semi-arid region. Due to the unfavorable distribution of surface water, to fulfill water demands and fluctuation of yearly seasonal streams, Iranian people have tried to provide a better condition for utilization of water as a vital matter. Iran is located in the south of Asia between 44º 02´ and 63º 20´ eastern longitude and 25º 03´ to 39º 46´ northern latitude. The country covers an area of about 1.648 million km2. -

University of Copenhagen
Abadan Elling, Rasmus Christian; Ehsani, Kaveh Published in: Middle East Report Publication date: 2018 Document version Early version, also known as pre-print Citation for published version (APA): Elling, R. C., & Ehsani, K. (2018). Abadan. Middle East Report, (287). Download date: 27. Sep. 2021 NOTE: This is authors' pre-print version. Reference should be made to the published version: Rasmus Christian Elling, Kaveh Ehsani: "Abadan," Middle East Report, No. 287 (Summer 2018). Abadan The Rise and Demise of an Oil Metropolis Kaveh Ehsani and Rasmus Christian Elling In fall 1978, Abadan’s oil refinery workers played a decisive role in the Iranian Revolution by joining the national mass strikes. Just two years later, Abadan and the adjoining port city of Khorramshahr were shelled by the invading Iraqi army and effectively destroyed during the Iran–Iraq war (1980–88), which scattered their population of over 600,000 as refugees across Iran and abroad. The bloody liberation of Khorramshahr (May 1982) turned the tide of Iraqi advances. Abadan’s refinery workers remarkably kept up production under constant shelling through eight years of war and international sanctions, earning the two cities a prominent place in post-revolutionary Iran’s official mythology of the “Sacred Defense.” Despite state propaganda lionizing the workers, postwar reconstruction has not been kind to either city.[1] Prior to the war, Khorramshahr had been Iran’s largest port, while the much larger Abadan was home to one of the world’s largest refineries. Both cities were major commercial centers in the late 1970s. A major tourist destination with posh resorts and nightclubs, cinemas and shopping centers [2], Abadan also boasted Iran’s second major international airport and a large bazaar. -
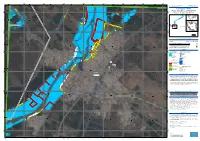
HAMIDIYEH, V1 Hamidiyeh - IRAN 0 0 0 0
254500 255000 255500 256000 256500 257000 257500 258000 48°24'40"E 48°25'0"E 48°25'20"E 48°25'40"E 48°26'0"E 48°26'20"E 48°26'40"E 48°27'0"E GLIDE number: FL-2019-000022-IRN Activation ID: EMSR352 Int. Charter call ID: 601 Product N.: 06HAMIDIYEH, v1 Hamidiyeh - IRAN 0 0 0 0 5 5 Flood - Situation as of 08/04/2019 7 7 8 8 4 4 3 3 Grading - Ready-to-print Map 01 N " 0 h 4 e ' h 9 rk 2 a ° K 1 3 Azerbaijan Turkmenistan Caspian N " 0 Sea 4 ' 9 2 ° 1 Tehran 3 ^ Dasht-e-Azadegan Hamidiyeh (! Khuzestan Iran Iraq RTP01 06 Kuwait Saudi Persian 0 0 Arabia Qatar 0 0 Gulf Gulf of Oman 0 0 7 7 8 8 4 4 3 3 6 km Cartographic Information 1:6000 Full color A1, 200 dpi resolution N " 0 2 ' 0 0,125 0,25 0,5 9 2 ° km 1 3 Grid: WGS 1984 UTM Zone 39N map coordinate system N " 0 2 ' Tick marks: WGS 84 geographical coordinate system 9 2 ± ° 1 3 Legend 0 0 0 0 5 5 6 6 8 8 Crisis Information Administrative boundaries 4 4 3 3 Flooded Area (08/04/2019 07:38 UTC) Province Flood trace Placenames ! Built Up Grading Placename Destroyed Hydrography Stream Damaged Reservoir Possibly damaged Transportation Grading River Road, Destroyed Stream Road, Damaged Transportation Bridge and elevated highway Road, Possibly damaged N " Primary Road 0 ' General Information 9 2 ° 1 3 Area of Interest Local Road 0 0 0 0 0 0 Cart Track N 6 6 " 8 8 0 ' 4 4 Ahvaz 9 2 3 3 ° 1 3 Map Information Hamidiyeh ! Severe flooding in several provinces of Iran since mid-March, has left 70 people dead. -

BASRA : ITS HISTORY, CULTURE and HERITAGE Basra Its History, Culture and Heritage
BASRA : ITS HISTORY, CULTURE AND HERITAGE CULTURE : ITS HISTORY, BASRA ITS HISTORY, CULTURE AND HERITAGE PROCEEDINGS OF THE CONFERENCE CELEBRATING THE OPENING OF THE BASRAH MUSEUM, SEPTEMBER 28–29, 2016 Edited by Paul Collins Edited by Paul Collins BASRA ITS HISTORY, CULTURE AND HERITAGE PROCEEDINGS OF THE CONFERENCE CELEBRATING THE OPENING OF THE BASRAH MUSEUM, SEPTEMBER 28–29, 2016 Edited by Paul Collins © BRITISH INSTITUTE FOR THE STUDY OF IRAQ 2019 ISBN 978-0-903472-36-4 Typeset and printed in the United Kingdom by Henry Ling Limited, at the Dorset Press, Dorchester, DT1 1HD CONTENTS Figures...................................................................................................................................v Contributors ........................................................................................................................vii Introduction ELEANOR ROBSON .......................................................................................................1 The Mesopotamian Marshlands (Al-Ahwār) in the Past and Today FRANCO D’AGOSTINO AND LICIA ROMANO ...................................................................7 From Basra to Cambridge and Back NAWRAST SABAH AND KELCY DAVENPORT ..................................................................13 A Reserve of Freedom: Remarks on the Time Visualisation for the Historical Maps ALEXEI JANKOWSKI ...................................................................................................19 The Pallakottas Canal, the Sealand, and Alexander STEPHANIE -

Water Resources Management in Karkheh Basin-Iran
PROCEEDINGS OF THE 3RD INTERNATIONAL CONFERENCE ON ENERGY AND DEVELOPMENT - ENVIRONMENT - BIOMEDICINE Water Resources Management in Karkheh Basin-Iran AMIR HAMZEH HAGHIABI1 , NIKOS E. MASTORAKIS2 1-Department of water engineering Lorestan University Khorramabad, Lorestan Province IRAN [email protected] 2- Technical University of Sofia, BULGARIA– also with the WSEAS Research Department, WSEAS, A.I.Theologou 17-23, Zografou, 15773, Athens, GREECE Abstract: - Karkheh basin is located in the semiarid and arid regions of Western Iran, an area with severe water scarcity. 70% of rainfall is directly evaporated. The potential annual evaporation of the southern and northern regions is 3,600 mm 1,800 mm, respectively. Agriculture plays an important role in the economy of the basin. In the present situation, 3.9 bm3 of water are used for irrigating 378,164 ha of irrigated agriculture (horticulture and field crops), and surface water and groundwater resources provide 63 percent and 37 percent, respectively, of this volume. Of the irrigated area, 76.5% is under cereals (wheat and barely), 23% under pulses, and 0.5% under cultivation of forage, orchards, melons and vegetables, and oil seeds. The area is particularly low in terms of yields, productivity and incomes. Irrigation efficiency in the basin is 28-36 percent and the overall Crop Water Productivity in the basin is about 0.55 kg/m3. In this paper, the specifications of the Karkheh Reservoir Dam & Hydroelectric Power Plant as the biggest dam in history of Iran with total volume of reservoir 7.3 Bm3 and Karkheh irrigation and drainage network project are illustrated. Also the situation of water availability in the basin, surface and groundwater potential and some aspects of water resources management in the basin are considered.