Distances in Astronomy
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Quantity Symbol Value One Astronomical Unit 1 AU 1.50 × 10
Quantity Symbol Value One Astronomical Unit 1 AU 1:50 × 1011 m Speed of Light c 3:0 × 108 m=s One parsec 1 pc 3.26 Light Years One year 1 y ' π × 107 s One Light Year 1 ly 9:5 × 1015 m 6 Radius of Earth RE 6:4 × 10 m Radius of Sun R 6:95 × 108 m Gravitational Constant G 6:67 × 10−11m3=(kg s3) Part I. 1. Describe qualitatively the funny way that the planets move in the sky relative to the stars. Give a qualitative explanation as to why they move this way. 2. Draw a set of pictures approximately to scale showing the sun, the earth, the moon, α-centauri, and the milky way and the spacing between these objects. Give an ap- proximate size for all the objects you draw (for example example next to the moon put Rmoon ∼ 1700 km) and the distances between the objects that you draw. Indicate many times is one picture magnified relative to another. Important: More important than the size of these objects is the relative distance between these objects. Thus for instance you may wish to show the sun and the earth on the same graph, with the circles for the sun and the earth having the correct ratios relative to to the spacing between the sun and the earth. 3. A common unit of distance in Astronomy is a parsec. 1 pc ' 3:1 × 1016m ' 3:3 ly (a) Explain how such a curious unit of measure came to be defined. Why is it called parsec? (b) What is the distance to the nearest stars and how was this distance measured? 4. -

Calculating Growing Degree Days by Jim Nugent District Horticulturist Michigan State University
Calculating Growing Degree Days By Jim Nugent District Horticulturist Michigan State University Are you calculating degree day accumulations and finding your values don't match the values being reported by MSU or your neighbor's electronic data collection unit? There is a logical reason! Three different methods are used to calculate degree days; i.e., 1) Averaging Method; 2) Baskerville-Emin (BE) Method; and 3) Electronic Real-time Data Collection. All methods attempt to calculate the heat accumulation above a minimum threshold temperature, often referred to the base temperature. Once both the daily maximum and minimum temperatures get above the minimum threshold temperature, (i.e., base temperature of 42degrees, 50degrees or whatever other base temperature of interest) then all methods are fairly comparable. However, differences do occur and these are accentuated in an exceptionally long period of cool spring temperatures, such as we experienced this year. Let me briefly explain: 1. Averaging Method: Easy to calculate Degree Days(DD) = Average daily temp. - Base Temp. = (max. + min.) / 2 - Base temp. If answer is negative, assume 0. Example: Calculate DD Base 50 given 65 degrees max. and 40 degrees min. Avg. = (65 + 40) / 2 = 52.5 degrees DD base 50 = 52.5 - 50 = 2.5 degrees. But look what happens given a maximum of 60 degrees and a minimum of 35 degrees: Avg. = (60 + 35) / 2 = 47.5 DD base 50 = 47.5 - 50 = -2.5 = 0 degrees. The maximum temperature was higher than the base of 50° , but no degree days were accumulated. A grower called about the first of June reporting only about 40% of the DD50 that we have recorded. -

Could a Nearby Supernova Explosion Have Caused a Mass Extinction? JOHN ELLIS* and DAVID N
Proc. Natl. Acad. Sci. USA Vol. 92, pp. 235-238, January 1995 Astronomy Could a nearby supernova explosion have caused a mass extinction? JOHN ELLIS* AND DAVID N. SCHRAMMtt *Theoretical Physics Division, European Organization for Nuclear Research, CH-1211, Geneva 23, Switzerland; tDepartment of Astronomy and Astrophysics, University of Chicago, 5640 South Ellis Avenue, Chicago, IL 60637; and *National Aeronautics and Space Administration/Fermilab Astrophysics Center, Fermi National Accelerator Laboratory, Batavia, IL 60510 Contributed by David N. Schramm, September 6, 1994 ABSTRACT We examine the possibility that a nearby the solar constant, supernova explosions, and meteorite or supernova explosion could have caused one or more of the comet impacts that could be due to perturbations of the Oort mass extinctions identified by paleontologists. We discuss the cloud. The first of these has little experimental support. possible rate of such events in the light of the recent suggested Nemesis (4), a conjectured binary companion of the Sun, identification of Geminga as a supernova remnant less than seems to have been excluded as a mechanism for the third,§ 100 parsec (pc) away and the discovery ofa millisecond pulsar although other possibilities such as passage of the solar system about 150 pc away and observations of SN 1987A. The fluxes through the galactic plane may still be tenable. The supernova of y-radiation and charged cosmic rays on the Earth are mechanism (6, 7) has attracted less research interest than some estimated, and their effects on the Earth's ozone layer are of the others, perhaps because there has not been a recent discussed. -

Distances and Magnitudes Distance Measurements the Cosmic Distance
Distances and Magnitudes Prof Andy Lawrence Astronomy 1G 2011-12 Distance Measurements Astronomy 1G 2011-12 The cosmic distance ladder • Distance measurements in astronomy are a chain, with each type of measurement relative to the one before • The bottom rung is the Astronomical Unit (AU), the (mean) distance between the Earth and the Sun • Many distance estimates rely on the idea of a "standard candle" or "standard yardstick" Astronomy 1G 2011-12 Distances in the solar system • relative distances to planets given by periods + Keplers law (see Lecture-2) • distance to Venus measured by radar • Sun-Earth = 1 A.U. (average) • Sun-Jupiter = 5 A.U. (average) • Sun-Neptune = 30 A.U. (average) • Sun- Oort cloud (comets) ~ 50,000 A.U. • 1 A.U. = 1.496 x 1011 m Astronomy 1G 2011-12 Distances to nearest stars • parallax against more distant non- moving stars • 1 parsec (pc) is defined as distance where parallax = 1 second of arc in standard units D = a/✓ (radians, metres) in AU and arcsec D(AU) = 1/✓rad = 206, 265/✓00 in parsec and arcsec D(pc) = 1/✓00 nearest star Proxima Centauri 1.30pc Very hard to measure less than 0.1" 1pc = 206,265 AU = 3.086 x 1016m so only good for stars a few parsecs away... until launch of GAIA mission in 2014..... Astronomy 1G 2011-12 More distant stars : standard candle technique If a star has luminosity L (total energy emitted per sec) then at L distance D we will observe flux density F (i.e. energy per second F = 2 per sq.m. -

A New Vla–Hipparcos Distance to Betelgeuse and Its Implications
The Astronomical Journal, 135:1430–1440, 2008 April doi:10.1088/0004-6256/135/4/1430 c 2008. The American Astronomical Society. All rights reserved. Printed in the U.S.A. A NEW VLA–HIPPARCOS DISTANCE TO BETELGEUSE AND ITS IMPLICATIONS Graham M. Harper1, Alexander Brown1, and Edward F. Guinan2 1 Center for Astrophysics and Space Astronomy, University of Colorado, Boulder, CO 80309, USA; [email protected], [email protected] 2 Department of Astronomy and Astrophysics, Villanova University, PA 19085, USA; [email protected] Received 2007 November 2; accepted 2008 February 8; published 2008 March 10 ABSTRACT The distance to the M supergiant Betelgeuse is poorly known, with the Hipparcos parallax having a significant uncertainty. For detailed numerical studies of M supergiant atmospheres and winds, accurate distances are a pre- requisite to obtaining reliable estimates for many stellar parameters. New high spatial resolution, multiwavelength, NRAO3 Very Large Array (VLA) radio positions of Betelgeuse have been obtained and then combined with Hipparcos Catalogue Intermediate Astrometric Data to derive new astrometric solutions. These new solutions indicate a smaller parallax, and hence greater distance (197 ± 45 pc), than that given in the original Hipparcos Catalogue (131 ± 30 pc) and in the revised Hipparcos reduction. They also confirm smaller proper motions in both right ascension and declination, as found by previous radio observations. We examine the consequences of the revised astrometric solution on Betelgeuse’s interaction with its local environment, on its stellar properties, and its kinematics. We find that the most likely star-formation scenario for Betelgeuse is that it is a runaway star from the Ori OB1 association and was originally a member of a high-mass multiple system within Ori OB1a. -
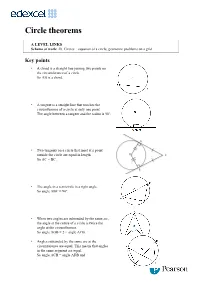
Circle Theorems
Circle theorems A LEVEL LINKS Scheme of work: 2b. Circles – equation of a circle, geometric problems on a grid Key points • A chord is a straight line joining two points on the circumference of a circle. So AB is a chord. • A tangent is a straight line that touches the circumference of a circle at only one point. The angle between a tangent and the radius is 90°. • Two tangents on a circle that meet at a point outside the circle are equal in length. So AC = BC. • The angle in a semicircle is a right angle. So angle ABC = 90°. • When two angles are subtended by the same arc, the angle at the centre of a circle is twice the angle at the circumference. So angle AOB = 2 × angle ACB. • Angles subtended by the same arc at the circumference are equal. This means that angles in the same segment are equal. So angle ACB = angle ADB and angle CAD = angle CBD. • A cyclic quadrilateral is a quadrilateral with all four vertices on the circumference of a circle. Opposite angles in a cyclic quadrilateral total 180°. So x + y = 180° and p + q = 180°. • The angle between a tangent and chord is equal to the angle in the alternate segment, this is known as the alternate segment theorem. So angle BAT = angle ACB. Examples Example 1 Work out the size of each angle marked with a letter. Give reasons for your answers. Angle a = 360° − 92° 1 The angles in a full turn total 360°. = 268° as the angles in a full turn total 360°. -

Angles ANGLE Topics • Coterminal Angles • Defintion of an Angle
Angles ANGLE Topics • Coterminal Angles • Defintion of an angle • Decimal degrees to degrees, minutes, seconds by hand using the TI-82 or TI-83 Plus • Degrees, seconds, minutes changed to decimal degree by hand using the TI-82 or TI-83 Plus • Standard position of an angle • Positive and Negative angles ___________________________________________________________________________ Definition: Angle An angle is created when a half-ray (the initial side of the angle) is drawn out of a single point (the vertex of the angle) and the ray is rotated around the point to another location (becoming the terminal side of the angle). An angle is created when a half-ray (initial side of angle) A: vertex point of angle is drawn out of a single point (vertex) AB: Initial side of angle. and the ray is rotated around the point to AC: Terminal side of angle another location (becoming the terminal side of the angle). Hence angle A is created (also called angle BAC) STANDARD POSITION An angle is in "standard position" when the vertex is at the origin and the initial side of the angle is along the positive x-axis. Recall: polynomials in algebra have a standard form (all the terms have to be listed with the term having the highest exponent first). In trigonometry, there is a standard position for angles. In this way, we are all talking about the same thing and are not trying to guess if your math solution and my math solution are the same. Not standard position. Not standard position. This IS standard position. Initial side not along Initial side along negative Initial side IS along the positive x-axis. -

Measuring the Astronomical Unit from Your Backyard Two Astronomers, Using Amateur Equipment, Determined the Scale of the Solar System to Better Than 1%
Measuring the Astronomical Unit from Your Backyard Two astronomers, using amateur equipment, determined the scale of the solar system to better than 1%. So can you. By Robert J. Vanderbei and Ruslan Belikov HERE ON EARTH we measure distances in millimeters and throughout the cosmos are based in some way on distances inches, kilometers and miles. In the wider solar system, to nearby stars. Determining the astronomical unit was as a more natural standard unit is the tUlronomical unit: the central an issue for astronomy in the 18th and 19th centu· mean distance from Earth to the Sun. The astronomical ries as determining the Hubble constant - a measure of unit (a.u.) equals 149,597,870.691 kilometers plus or minus the universe's expansion rate - was in the 20th. just 30 meters, or 92,955.807.267 international miles plus or Astronomers of a century and more ago devised various minus 100 feet, measuring from the Sun's center to Earth's ingenious methods for determining the a. u. In this article center. We have learned the a. u. so extraordinarily well by we'll describe a way to do it from your backyard - or more tracking spacecraft via radio as they traverse the solar sys precisely, from any place with a fairly unobstructed view tem, and by bouncing radar Signals off solar.system bodies toward the east and west horizons - using only amateur from Earth. But we used to know it much more poorly. equipment. The method repeats a historic experiment per This was a serious problem for many brancht:s of as formed by Scottish astronomer David Gill in the late 19th tronomy; the uncertain length of the astronomical unit led century. -

Guide for the Use of the International System of Units (SI)
Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S. -

Measuring the Speed of Light and the Moon Distance with an Occultation of Mars by the Moon: a Citizen Astronomy Campaign
Measuring the speed of light and the moon distance with an occultation of Mars by the Moon: a Citizen Astronomy Campaign Jorge I. Zuluaga1,2,3,a, Juan C. Figueroa2,3, Jonathan Moncada4, Alberto Quijano-Vodniza5, Mario Rojas5, Leonardo D. Ariza6, Santiago Vanegas7, Lorena Aristizábal2, Jorge L. Salas8, Luis F. Ocampo3,9, Jonathan Ospina10, Juliana Gómez3, Helena Cortés3,11 2 FACom - Instituto de Física - FCEN, Universidad de Antioquia, Medellín-Antioquia, Colombia 3 Sociedad Antioqueña de Astronomía, Medellín-Antioquia, Colombia 4 Agrupación Castor y Pollux, Arica, Chile 5 Observatorio Astronómico Universidad de Nariño, San Juan de Pasto-Nariño, Colombia 6 Asociación de Niños Indagadores del Cosmos, ANIC, Bogotá, Colombia 7 Organización www.alfazoom.info, Bogotá, Colombia 8 Asociación Carabobeña de Astronomía, San Diego-Carabobo, Venezuela 9 Observatorio Astronómico, Instituto Tecnológico Metropolitano, Medellín, Colombia 10 Sociedad Julio Garavito Armero para el Estudio de la Astronomía, Medellín, Colombia 11 Planetario de Medellín, Parque Explora, Medellín, Colombia ABSTRACT In July 5th 2014 an occultation of Mars by the Moon was visible in South America. Citizen scientists and professional astronomers in Colombia, Venezuela and Chile performed a set of simple observations of the phenomenon aimed to measure the speed of light and lunar distance. This initiative is part of the so called “Aristarchus Campaign”, a citizen astronomy project aimed to reproduce observations and measurements made by astronomers of the past. Participants in the campaign used simple astronomical instruments (binoculars or small telescopes) and other electronic gadgets (cell-phones and digital cameras) to measure occultation times and to take high resolution videos and pictures. In this paper we describe the results of the Aristarchus Campaign. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

Lecture 5: Stellar Distances 10/2/19, 8�02 AM
Lecture 5: Stellar Distances 10/2/19, 802 AM Astronomy 162: Introduction to Stars, Galaxies, & the Universe Prof. Richard Pogge, MTWThF 9:30 Lecture 5: Distances of the Stars Readings: Ch 19, section 19-1 Key Ideas Distance is the most important & most difficult quantity to measure in Astronomy Method of Trigonometric Parallaxes Direct geometric method of finding distances Units of Cosmic Distance: Light Year Parsec (Parallax second) Why are Distances Important? Distances are necessary for estimating: Total energy emitted by an object (Luminosity) Masses of objects from their orbital motions True motions through space of stars Physical sizes of objects The problem is that distances are very hard to measure... The problem of measuring distances Question: How do you measure the distance of something that is beyond the reach of your measuring instruments? http://www.astronomy.ohio-state.edu/~pogge/Ast162/Unit1/distances.html Page 1 of 7 Lecture 5: Stellar Distances 10/2/19, 802 AM Examples of such problems: Large-scale surveying & mapping problems. Military range finding to targets Measuring distances to any astronomical object Answer: You resort to using GEOMETRY to find the distance. The Method of Trigonometric Parallaxes Nearby stars appear to move with respect to more distant background stars due to the motion of the Earth around the Sun. This apparent motion (it is not "true" motion) is called Stellar Parallax. (Click on the image to view at full scale [Size: 177Kb]) In the picture above, the line of sight to the star in December is different than that in June, when the Earth is on the other side of its orbit.