DOCSLIB.ORG

Chapter 2: Internal Energy (U), Work (W), Heat (Q), Enthalpy (H)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 2: Internal Energy (U), Work (W), Heat (Q), Enthalpy (H) Winter 2013 Chem 254: Introductory Thermodynamics Chapter 2: Internal Energy (U), Work (w), Heat (q), Enthalpy (H) ................................................ 13 Heat Capacities ......................................................................................................................... 16 Calculating ΔU, ΔH, w, q in Ideal Gas ........................................................................................ 18 Isothermal Compression ........................................................................................................... 21 Reversible Process (limiting process) ....................................................................................... 22 Isothermal Expansion ............................................................................................................... 22 Chapter 2: Internal Energy (U), Work (w), Heat (q), Enthalpy (H) Internal Energy (excludes motion and rotation of vessel) Look at isolated part of universe UUUsystem Environment Total = isolated First law of thermodynamics: - Total U for isolated system is constant - Energy can be exchanged between various components - Energy forms can be interconverted Eg. Chemical En Heat Work UUUtotal system environement 0 Chapter 2: Internal Energy, Work, Heat and Enthalpy 13 Winter 2013 Chem 254: Introductory Thermodynamics Work In classical mechanics, move object a distance d with force F in direction of displacement is work N m = J F mg dh w mgh (kg m s-2 m = N m = J) h w mgd cos cos d h w mgd mgh d General formula w F dL Line integral PV work (constant external pressure) F m applies constant force P A F w mgh Fh ()() Ah P V V A ext 12 w Pext() V final V initial Joules, or L Bar (1 L Bar = 100 J) Chapter 2: Internal Energy, Work, Heat and Enthalpy 14 Winter 2013 Chem 254: Introductory Thermodynamics More general formula for PV work, P does not need to be constant Vf w P dV V ext i Sign Convention : Work done on the system raises internal energy of system ( w 0) Work done by the system lowers the internal energy ( w 0) Other forms of work: - electrical work wQ Q is charge in coulombs difference in potential (in Volts or J/C) Run a current over Q I t I is current (in Amps or C/s) w I t Important: Work is associated with a process, with change. Work is transitory. You cannot say that a system contains that amount of energy or heat Heat: associated with a process going from State 1 State 2 Usystem q w q is heat; w is the work Heat is exchanged between system and environment q 0: system loses energy q 0 : system gains energy qqsystem environment note: TTsystem environment for heat to flow Isolated system Chapter 2: Internal Energy, Work, Heat and Enthalpy 15 Winter 2013 Chem 254: Introductory Thermodynamics TTouter inner (regulate) So there is no flow of heat UUsystem environment 0 Uinner 0 Beaker + Lab +… = environment (isolated) UI 0; UII 0 UUI II 0 Chemical Energy Butane + O2 CO 2 H 2 Note : UII 0even if temperature increases! Why? Chemical energy of butane is converted to heat. Heat Capacities The amount of energy (heat) required to raise the temperature of 1 gram of substance by 1 oC. Heat capacity of water is 4.18 J/g K = 1 calorie 1) Heat capacity is dependent on heat Eg. 10 oC 11 oC and 80 oC 81 oC, require slightly different energies 2) At least 2 types of heat capacity a) Keep volume constant CV b) Keep pressure constant CP 3) Heat capacity is proportional to amount of substance Molar heat capacities : CPm, ,CVm, n moles : CV nC V, m , CP nC P, m 4) General formula Chapter 2: Internal Energy, Work, Heat and Enthalpy 16 Winter 2013 Chem 254: Introductory Thermodynamics Tf q C dT VVT i If CV is constant over temperature range: T f Tf qV C V dT C V T C V T f T i T Ti i qVV C() T And qPP C() T Which is larger CP or CV ? Relation for and for ideal gas? VV21 ; TT21 U qP w q P P ext () V21 V PV nRT U qP nR() T21 T qPP C T ; U qVV C T CPV T C T nR T CPV C nR or CCRP,, m V m Therefore CP is larger than CV . At constant P , the system also does PV work when raising T . (analysis for ideal gas) No work because V is constant U qV w qV UCT V Bomb calorimetry qsystem q surrounding C Calorimeter T V V V measure U reaction Chapter 2: Internal Energy, Work, Heat and Enthalpy 17 Winter 2013 Chem 254: Introductory Thermodynamics system surroundings qqPV system Calorimeter qP C V T measure system qHP reaction True definition of Enthalpy H U () PV PV PV2 2 PV 1 1 ; for PV1 1 PV 2 2 ; H U PV At constant Pressure H U PV2 2 PV 1 1 HUPV H qPP w P V q P()() V P V H qPP C T Completely general :UH, are function of state specify TVP,, UUTPVUTPV (,,)(,,)2 2 2 1 1 1 HHTPVHTPV (,,)(,,) 2 2 2 1 1 1 Change in UH, are the same for both paths Change in qw, are different for different paths Calculating ΔU, ΔH, w, q in Ideal Gas 1) Calculating UH, is easy if T is known T f Tf UUT()] U CdTCT CT T T V V Ti V f i i UCT V for any process HHT( ) ..... Chapter 2: Internal Energy, Work, Heat and Enthalpy 18 Winter 2013 Chem 254: Introductory Thermodynamics HCT P for any process (if CP is constant) We know CPV C nR Special cases: Isothermal Process T is constant T 0 ; UH 0 2) Work: w P dV PV work only ext - Constant V Vif V w 0 ; q qV U Vf - Constant Pext w P dV P() V V ; q q H extV ext f i P i Isothermal reversible process: (Reversible process: delicate, see later) 1 P nRT nRT is constant ext V Vf dV V w nRT nRTln V f V Vi i V Vf nRTln Vfi ln V nRT ln Vi Vf w nRT ln Vi 3) Heat Adiabatic process : q 0 by definition U q w; Uw Adiabatic Reversible Process nRT q 0 , Uw, P ext V Vf nRT U w dV V i V nRT nC dT dV Vm, V dT nR nC dV Vm, TV Chapter 2: Internal Energy, Work, Heat and Enthalpy 19 Winter 2013 Chem 254: Introductory Thermodynamics ffdT dV nC nR Vm, iiTV TVff nCvm, ln nR ln TVii Cvm, TVff ln ln RTVii For adiabatic reversible process: C TV C T P V C P vm, lnff ln OR Pm, lnf ln i OR lnf Pm, ln i RTVii RTPif VCPi V, m f 1) R C TVVf R f f Vm, ln ln ln TCVVi V, m i i R C TVffVm, TVii 2) C T nRT P Vm, lnff ln i R Ti P f nRT i T P ln f i TPif T P lnf ln i TPif C T P Vm, 1 lnf ln i RTPif CRVm, Tf Pi ln ln RTP if C T P Pm, lnf ln i RTPif Chapter 2: Internal Energy, Work, Heat and Enthalpy 20 Winter 2013 Chem 254: Introductory Thermodynamics Adiabatic Isobaric Process Constant external pressure AND q 0 Isothermal Compression Constant external pressure w Pf V f V i 0 qw 0 (because U 0 because isothermal) What is work in 2-step process? w2 P int V int Vi P f V f V int ww21 ; qq21 Chapter 2: Internal Energy, Work, Heat and Enthalpy 21 Winter 2013 Chem 254: Introductory Thermodynamics Conclusion: w and q depend on details of process, not only on initial and final state. Repeat for 3 step, 4…. w5 w 4 w 3 w 2 w 1 ; q5 q 4 q 3 q 2 q 1 The more steps, the less w and less heat Reversible Process (limiting process) PPext gas at each step nRT P ext V Isothermal Reversible Process VVffdV w P dV nRT VVext iiV V Vf f nRTln | nRT ln work, q is minimal Vi Vi Isothermal Expansion Chapter 2: Internal Energy, Work, Heat and Enthalpy 22 Winter 2013 Chem 254: Introductory Thermodynamics w1 Pf V f V i 0 ; qw11 0 ww21 ; qq21 w3 w 2 w 1 ; q3 q 2 q 1 More processes more work ( w ), more heat ( q ) w5 w 4 w 3 w 2 w 1 ; q5 q 4 q 3 q 2 q 1 Limiting Expansion Work compressionexp ansion wwlimit limit VVffdV Vf w P dV nRT nRT ln limit VVext ii VVi Chapter 2: Internal Energy, Work, Heat and Enthalpy 23 Winter 2013 Chem 254: Introductory Thermodynamics Grains of sand : I can run process either way The thermodynamic work is the same both ways for reversible process Irreversible Process (Big chunks of mass) Follows arrows in reverse: add mass, piston rises? ; removes mass, piston lowers? This is absurd, hence: Why do irreversible processes run in one way and not another? What is special about irreversible? Chapter 2: Internal Energy, Work, Heat and Enthalpy 24 .
Load more

Recommended publications
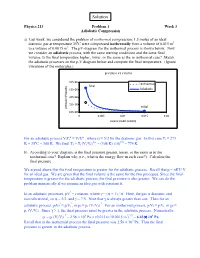
  • 3-1 Adiabatic Compression
    Solution Physics 213 Problem 1 Week 3 Adiabatic Compression a) Last week, we considered the problem of isothermal compression: 1.5 moles of an ideal diatomic gas at temperature 35oC were compressed isothermally from a volume of 0.015 m3 to a volume of 0.0015 m3. The pV-diagram for the isothermal process is shown below. Now we consider an adiabatic process, with the same starting conditions and the same final volume. Is the final temperature higher, lower, or the same as the in isothermal case? Sketch the adiabatic processes on the p-V diagram below and compute the final temperature. (Ignore vibrations of the molecules.) α α For an adiabatic process ViTi = VfTf , where α = 5/2 for the diatomic gas. In this case Ti = 273 o 1/α 2/5 K + 35 C = 308 K. We find Tf = Ti (Vi/Vf) = (308 K) (10) = 774 K. b) According to your diagram, is the final pressure greater, lesser, or the same as in the isothermal case? Explain why (i.e., what is the energy flow in each case?). Calculate the final pressure. We argued above that the final temperature is greater for the adiabatic process. Recall that p = nRT/ V for an ideal gas. We are given that the final volume is the same for the two processes. Since the final temperature is greater for the adiabatic process, the final pressure is also greater. We can do the problem numerically if we assume an idea gas with constant α. γ In an adiabatic processes, pV = constant, where γ = (α + 1) / α.
    [Show full text]
  • Thermodynamics of Solar Energy Conversion in to Work
    Sri Lanka Journal of Physics, Vol. 9 (2008) 47-60 Institute of Physics - Sri Lanka Research Article Thermodynamic investigation of solar energy conversion into work W.T.T. Dayanga and K.A.I.L.W. Gamalath Department of Physics, University of Colombo, Colombo 03, Sri Lanka Abstract Using a simple thermodynamic upper bound efficiency model for the conversion of solar energy into work, the best material for a converter was obtained. Modifying the existing detailed terrestrial application model of direct solar radiation to include an atmospheric transmission coefficient with cloud factors and a maximum concentration ratio, the best shape for a solar concentrator was derived. Using a Carnot engine in detailed space application model, the best shape for the mirror of a concentrator was obtained. A new conversion model was introduced for a solar chimney power plant to obtain the efficiency of the power plant and power output. 1. INTRODUCTION A system that collects and converts solar energy in to mechanical or electrical power is important from various aspects. There are two major types of solar power systems at present, one using photovoltaic cells for direct conversion of solar radiation energy in to electrical energy in combination with electrochemical storage and the other based on thermodynamic cycles. The efficiency of a solar thermal power plant is significantly higher [1] compared to the maximum efficiency of twenty percent of a solar cell. Although the initial cost of a solar thermal power plant is very high, the running cost is lower compared to the other power plants. Therefore most countries tend to build solar thermal power plants.
    [Show full text]
  • Lecture 4: 09.16.05 Temperature, Heat, and Entropy
    3.012 Fundamentals of Materials Science Fall 2005 Lecture 4: 09.16.05 Temperature, heat, and entropy Today: LAST TIME .........................................................................................................................................................................................2� State functions ..............................................................................................................................................................................2� Path dependent variables: heat and work..................................................................................................................................2� DEFINING TEMPERATURE ...................................................................................................................................................................4� The zeroth law of thermodynamics .............................................................................................................................................4� The absolute temperature scale ..................................................................................................................................................5� CONSEQUENCES OF THE RELATION BETWEEN TEMPERATURE, HEAT, AND ENTROPY: HEAT CAPACITY .......................................6� The difference between heat and temperature ...........................................................................................................................6� Defining heat capacity.................................................................................................................................................................6�
    [Show full text]
  • Vapour Absorption Refrigeration Systems Based on Ammonia- Water Pair
    Lesson 17 Vapour Absorption Refrigeration Systems Based On Ammonia- Water Pair Version 1 ME, IIT Kharagpur 1 The specific objectives of this lesson are to: 1. Introduce ammonia-water systems (Section 17.1) 2. Explain the working principle of vapour absorption refrigeration systems based on ammonia-water (Section 17.2) 3. Explain the principle of rectification column and dephlegmator (Section 17.3) 4. Present the steady flow analysis of ammonia-water systems (Section 17.4) 5. Discuss the working principle of pumpless absorption refrigeration systems (Section 17.5) 6. Discuss briefly solar energy based sorption refrigeration systems (Section 17.6) 7. Compare compression systems with absorption systems (Section 17.7) At the end of the lecture, the student should be able to: 1. Draw the schematic of a ammonia-water based vapour absorption refrigeration system and explain its working principle 2. Explain the principle of rectification column and dephlegmator using temperature-concentration diagrams 3. Carry out steady flow analysis of absorption systems based on ammonia- water 4. Explain the working principle of Platen-Munter’s system 5. List solar energy driven sorption refrigeration systems 6. Compare vapour compression systems with vapour absorption systems 17.1. Introduction Vapour absorption refrigeration system based on ammonia-water is one of the oldest refrigeration systems. As mentioned earlier, in this system ammonia is used as refrigerant and water is used as absorbent. Since the boiling point temperature difference between ammonia and water is not very high, both ammonia and water are generated from the solution in the generator. Since presence of large amount of water in refrigerant circuit is detrimental to system performance, rectification of the generated vapour is carried out using a rectification column and a dephlegmator.
    [Show full text]
  • Chapter 3. Second and Third Law of Thermodynamics
    Chapter 3. Second and third law of thermodynamics Important Concepts Review Entropy; Gibbs Free Energy • Entropy (S) – definitions Law of Corresponding States (ch 1 notes) • Entropy changes in reversible and Reduced pressure, temperatures, volumes irreversible processes • Entropy of mixing of ideal gases • 2nd law of thermodynamics • 3rd law of thermodynamics Math • Free energy Numerical integration by computer • Maxwell relations (Trapezoidal integration • Dependence of free energy on P, V, T https://en.wikipedia.org/wiki/Trapezoidal_rule) • Thermodynamic functions of mixtures Properties of partial differential equations • Partial molar quantities and chemical Rules for inequalities potential Major Concept Review • Adiabats vs. isotherms p1V1 p2V2 • Sign convention for work and heat w done on c=C /R vm system, q supplied to system : + p1V1 p2V2 =Cp/CV w done by system, q removed from system : c c V1T1 V2T2 - • Joule-Thomson expansion (DH=0); • State variables depend on final & initial state; not Joule-Thomson coefficient, inversion path. temperature • Reversible change occurs in series of equilibrium V states T TT V P p • Adiabatic q = 0; Isothermal DT = 0 H CP • Equations of state for enthalpy, H and internal • Formation reaction; enthalpies of energy, U reaction, Hess’s Law; other changes D rxn H iD f Hi i T D rxn H Drxn Href DrxnCpdT Tref • Calorimetry Spontaneous and Nonspontaneous Changes First Law: when one form of energy is converted to another, the total energy in universe is conserved. • Does not give any other restriction on a process • But many processes have a natural direction Examples • gas expands into a vacuum; not the reverse • can burn paper; can't unburn paper • heat never flows spontaneously from cold to hot These changes are called nonspontaneous changes.
    [Show full text]
  • Chapter 8 and 9 – Energy Balances
    CBE2124, Levicky Chapter 8 and 9 – Energy Balances Reference States . Recall that enthalpy and internal energy are always defined relative to a reference state (Chapter 7). When solving energy balance problems, it is therefore necessary to define a reference state for each chemical species in the energy balance (the reference state may be predefined if a tabulated set of data is used such as the steam tables). Example . Suppose water vapor at 300 oC and 5 bar is chosen as a reference state at which Hˆ is defined to be zero. Relative to this state, what is the specific enthalpy of liquid water at 75 oC and 1 bar? What is the specific internal energy of liquid water at 75 oC and 1 bar? (Use Table B. 7). Calculating changes in enthalpy and internal energy. Hˆ and Uˆ are state functions , meaning that their values only depend on the state of the system, and not on the path taken to arrive at that state. IMPORTANT : Given a state A (as characterized by a set of variables such as pressure, temperature, composition) and a state B, the change in enthalpy of the system as it passes from A to B can be calculated along any path that leads from A to B, whether or not the path is the one actually followed. Example . 18 g of liquid water freezes to 18 g of ice while the temperature is held constant at 0 oC and the pressure is held constant at 1 atm. The enthalpy change for the process is measured to be ∆ Hˆ = - 6.01 kJ.
    [Show full text]
  • HEAT and TEMPERATURE Heat Is a Type of ENERGY. When Absorbed
    HEAT AND TEMPERATURE Heat is a type of ENERGY. When absorbed by a substance, heat causes inter-particle bonds to weaken and break which leads to a change of state (solid to liquid for example). Heat causing a phase change is NOT sufficient to cause an increase in temperature. Heat also causes an increase of kinetic energy (motion, friction) of the particles in a substance. This WILL cause an increase in TEMPERATURE. Temperature is NOT energy, only a measure of KINETIC ENERGY The reason why there is no change in temperature at a phase change is because the substance is using the heat only to change the way the particles interact (“stick together”). There is no increase in the particle motion and hence no rise in temperature. THERMAL ENERGY is one type of INTERNAL ENERGY possessed by an object. It is the KINETIC ENERGY component of the object’s internal energy. When thermal energy is transferred from a hot to a cold body, the term HEAT is used to describe the transferred energy. The hot body will decrease in temperature and hence in thermal energy. The cold body will increase in temperature and hence in thermal energy. Temperature Scales: The K scale is the absolute temperature scale. The lowest K temperature, 0 K, is absolute zero, the temperature at which an object possesses no thermal energy. The Celsius scale is based upon the melting point and boiling point of water at 1 atm pressure (0, 100o C) K = oC + 273.13 UNITS OF HEAT ENERGY The unit of heat energy we will use in this lesson is called the JOULE (J).
    [Show full text]
  • Solar Thermal Energy
    22 Solar Thermal Energy Solar thermal energy is an application of solar energy that is very different from photovol- taics. In contrast to photovoltaics, where we used electrodynamics and solid state physics for explaining the underlying principles, solar thermal energy is mainly based on the laws of thermodynamics. In this chapter we give a brief introduction to that field. After intro- ducing some basics in Section 22.1, we will discuss Solar Thermal Heating in Section 22.2 and Concentrated Solar (electric) Power (CSP) in Section 22.3. 22.1 Solar thermal basics We start this section with the definition of heat, which sometimes also is called thermal energy . The molecules of a body with a temperature different from 0 K exhibit a disordered movement. The kinetic energy of this movement is called heat. The average of this kinetic energy is related linearly to the temperature of the body. 1 Usually, we denote heat with the symbol Q. As it is a form of energy, its unit is Joule (J). If two bodies with different temperatures are brought together, heat will flow from the hotter to the cooler body and as a result the cooler body will be heated. Dependent on its physical properties and temperature, this heat can be absorbed in the cooler body in two forms, sensible heat and latent heat. Sensible heat is that form of heat that results in changes in temperature. It is given as − Q = mC p(T2 T1), (22.1) where Q is the amount of heat that is absorbed by the body, m is its mass, Cp is its heat − capacity and (T2 T1) is the temperature difference.
    [Show full text]
  • Thermodynamics Formulation of Economics Burin Gumjudpai A
    Thermodynamics Formulation of Economics 306706052 NIDA E-THESIS 5710313001 thesis / recv: 09012563 15:07:41 seq: 16 Burin Gumjudpai A Thesis Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Economics (Financial Economics) School of Development Economics National Institute of Development Administration 2019 Thermodynamics Formulation of Economics Burin Gumjudpai School of Development Economics Major Advisor (Associate Professor Yuthana Sethapramote, Ph.D.) The Examining Committee Approved This Thesis Submitted in Partial 306706052 Fulfillment of the Requirements for the Degree of Master of Economics (Financial Economics). Committee Chairperson NIDA E-THESIS 5710313001 thesis / recv: 09012563 15:07:41 seq: 16 (Assistant Professor Pongsak Luangaram, Ph.D.) Committee (Assistant Professor Athakrit Thepmongkol, Ph.D.) Committee (Associate Professor Yuthana Sethapramote, Ph.D.) Dean (Associate Professor Amornrat Apinunmahakul, Ph.D.) ______/______/______ ABST RACT ABSTRACT Title of Thesis Thermodynamics Formulation of Economics Author Burin Gumjudpai Degree Master of Economics (Financial Economics) Year 2019 306706052 We consider a group of information-symmetric consumers with one type of commodity in an efficient market. The commodity is fixed asset and is non-disposable. We are interested in seeing if there is some connection of thermodynamics formulation NIDA E-THESIS 5710313001 thesis / recv: 09012563 15:07:41 seq: 16 to microeconomics. We follow Carathéodory approach which requires empirical existence of equation of state (EoS) and coordinates before performing maximization of variables. In investigating EoS of various system for constructing the economics EoS, unexpectedly new insights of thermodynamics are discovered. With definition of truly endogenous function, criteria rules and diagrams are proposed in identifying the status of EoS for an empirical equation.
    [Show full text]
  • A Comparative Energy and Economic Analysis Between a Low Enthalpy Geothermal Design and Gas, Diesel and Biomass Technologies for a HVAC System Installed in an Office Building
    energies Article A Comparative Energy and Economic Analysis between a Low Enthalpy Geothermal Design and Gas, Diesel and Biomass Technologies for a HVAC System Installed in an Office Building José Ignacio Villarino 1, Alberto Villarino 1,* , I. de Arteaga 2 , Roberto Quinteros 2 and Alejandro Alañón 1 1 Department of Construction and Agronomy, Construction Engineering Area, High Polytechnic School of Ávila, University of Salamanca, Hornos Caleros, 50, 05003 Ávila, Spain; [email protected] (J.I.V.); [email protected] (A.A.) 2 Facultad de Ingeniería, Escuela de Ingeniería Mecánica, Pontificia Universidad Católica de Valparaíso, Av. Los Carrera 01567, Quilpué 2430000, Chile; [email protected] (I.d.A.); [email protected] (R.Q.) * Correspondence: [email protected]; Tel.: +34-920-353-500; Fax: +34-920-353-501 Received: 3 January 2019; Accepted: 25 February 2019; Published: 6 March 2019 Abstract: This paper presents an analysis of economic and energy between a ground-coupled heat pump system and other available technologies, such as natural gas, biomass, and diesel, providing heating, ventilation, and air conditioning to an office building. All the proposed systems are capable of reaching temperatures of 22 ◦C/25 ◦C in heating and cooling modes. EnergyPlus software was used to develop a simulation model and carry out the validation process. The first objective of the paper is the validation of the numerical model developed in EnergyPlus with the experimental results collected from the monitored building to evaluate the system in other operating conditions and to compare it with other available technologies. The second aim of the study is the assessment of the position of the low enthalpy geothermal system proposed versus the rest of the systems, from energy, economic, and environmental aspects.
    [Show full text]
  • Work and Energy Summary Sheet Chapter 6
    Work and Energy Summary Sheet Chapter 6 Work: work is done when a force is applied to a mass through a displacement or W=Fd. The force and the displacement must be parallel to one another in order for work to be done. F (N) W =(Fcosθ)d F If the force is not parallel to The area of a force vs. the displacement, then the displacement graph + W component of the force that represents the work θ d (m) is parallel must be found. done by the varying - W d force. Signs and Units for Work Work is a scalar but it can be positive or negative. Units of Work F d W = + (Ex: pitcher throwing ball) 1 N•m = 1 J (Joule) F d W = - (Ex. catcher catching ball) Note: N = kg m/s2 • Work – Energy Principle Hooke’s Law x The work done on an object is equal to its change F = kx in kinetic energy. F F is the applied force. 2 2 x W = ΔEk = ½ mvf – ½ mvi x is the change in length. k is the spring constant. F Energy Defined Units Energy is the ability to do work. Same as work: 1 N•m = 1 J (Joule) Kinetic Energy Potential Energy Potential energy is stored energy due to a system’s shape, position, or Kinetic energy is the energy of state. motion. If a mass has velocity, Gravitational PE Elastic (Spring) PE then it has KE 2 Mass with height Stretch/compress elastic material Ek = ½ mv 2 EG = mgh EE = ½ kx To measure the change in KE Change in E use: G Change in ES 2 2 2 2 ΔEk = ½ mvf – ½ mvi ΔEG = mghf – mghi ΔEE = ½ kxf – ½ kxi Conservation of Energy “The total energy is neither increased nor decreased in any process.
    [Show full text]
  • Muddiest Point – Entropy and Reversible I Am Confused About Entropy and How It Is Different in a Reversible Versus Irreversible Case
    1 Muddiest Point { Entropy and Reversible I am confused about entropy and how it is different in a reversible versus irreversible case. Note: Some of the discussion below follows from the previous muddiest points comment on the general idea of a reversible and an irreversible process. You may wish to have a look at that comment before reading this one. Let's talk about entropy first, and then we will consider how \reversible" gets involved. Generally we divide the universe into two parts, a system (what we are studying) and the surrounding (everything else). In the end the total change in the entropy will be the sum of the change in both, dStotal = dSsystem + dSsurrounding: This total change of entropy has only two possibilities: Either there is no spontaneous change (equilibrium) and dStotal = 0, or there is a spontaneous change because we are not at equilibrium, and dStotal > 0. Of course the entropy change of each piece, system or surroundings, can be positive or negative. However, the second law says the sum must be zero or positive. Let's start by thinking about the entropy change in the system and then we will add the entropy change in the surroundings. Entropy change in the system: When you consider the change in entropy for a process you should first consider whether or not you are looking at an isolated system. Start with an isolated system. An isolated system is not able to exchange energy with anything else (the surroundings) via heat or work. Think of surrounding the system with a perfect, rigid insulating blanket.
    [Show full text]