DOCSLIB.ORG

Pseudoforest Partitions and the Approximation of Connected Subgraphs of High Density

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Pseudoforest Partitions and the Approximation of Connected Subgraphs of High Density PSEUDOFORESTPARTITIONS ANDTHEAPPROXIMATIONOF CONNECTEDSUBGRAPHSOFHIGHDENSITY Dissertation zur Erlangung des Grades „Doktor der Naturwissenschaften“ am Fachbereich Physik, Mathematik und Informatik der Johannes Gutenberg-Universität in Mainz vorgelegt von Markus Andreas Daniel Blumenstock geboren in Frankfurt am Main Mainz, den 8. Januar 2020 Typographisch korrigierte Fassung vom 19. Juni 2020 erstberichterstatter: Prof. Dr. Ernst Althaus zweitberichterstatter: Prof. Dr. Andreas Hildebrandt drittberichterstatter: Prof. Dr. Ulrich Meyer Datum des Kolloquiums: 12.11.2019 D77 ZUSAMMENFASSUNG In dieser Arbeit werden das Problem, in einem einfachen Graphen einen Subgraphen mit maximaler Dichte d∗ zu finden, sowie verwand- te Probleme diskutiert. Die ganzzahlige Variante des dazu dualen Problems ist, eine Orientierung mit kleinstmöglichem maximalen Ein- gangsgrad zu finden. Dieser Eingangsgrad ist gleich der kleinsten Anzahl an Pseudowäldern, in die der Graph zerlegt werden kann, und wird daher als Pseudoarborizität p bezeichnet. Es wird gezeigt, wie Kowaliks Approximationsschema dazu ver- wendet werden kann, die balancierte binäre Suche des Algorithmus von Gabow und Westermann zu beschleunigen und eine Laufzeit von p (m3/2 log log p) für die Bestimmung von p zu erreichen, wobei O m die Anzahl der Kanten des Graphen ist. Ein Subgraph mit Dichte größer d 1 kann mit derselben asymptotischen Laufzeit bestimmt d ∗e − werden. Es werden zudem Laufzeiten verschiedener Algorithmen zur Bestimmung von p experimentell verglichen. Mit aktueller Hardwa- re können die Berechnungen für soziale Netzwerke mit hunderten Millionen Kanten in wenigen Minuten ausgeführt werden. Aufbauend auf Kowaliks Approximationsschema wird ein Appro- ximationsschema für die Arborizität eines Graphen mit derselben Laufzeit entwickelt. Im Gegensatz zu früheren Ansätzen approximiert dieses nicht nur den Wert der Arborizität, sondern berechnet auch eine dazugehörige Zerlegung in Wälder. Dies wird durch eine schnelle Konvertierung von k Pseudowäldern in k + 1 Wälder erreicht. Basierend auf dem Konzept der maximalen Dichte kann ein gemischt- ganzzahliges lineares Programm (MILP) aufgestellt werden, um zu- sammenhängende Subgraphen zu finden, die eine lineare Funktion minimieren. Dieses Problem, das eng mit dem Steinerbaumproblem auf Graphen verwandt ist, ist im Allgemeinen NP-schwer. Für den Fall, dass die Anzahl der Knoten des Subgraphen genau k betragen soll, wird das MILP mit einer anderen bestehenden Formulierung, den generalized subtour elimination constraints (GSEC), sowohl theoretisch als auch experimentell verglichen. Eine weiteres Thema, das beleuchtet wird, ist die Approximation des Steinerbaumproblems auf Graphen mithilfe der bidirected cut re- laxation (BCR), welche äquivalent zu GSEC ist. Es wird gezeigt, dass der Algorithmus von Byrka et al. eine 1,354-Approximation berechnet, wenn die Instanzen keine Steinerklauen enthalten. Es wird zudem eine Idee zur Generierung schwieriger Instanzen vorgestellt, die jedoch nicht in verbesserten unteren Schranken an das integrality gap von BCR resultiert. iii ABSTRACT This thesis deals with the problem of finding a subgraph of maximum density d∗ in a simple graph and related problems. The integral variant of the dual problem is to find an orientation with the smallest possible maximum indegree. This indegree is equal to the smallest number p of pseudoforests into which the graph can be partitioned, and is therefore called pseudoarboricity. It is shown that Kowalik’s approximation scheme can be employed to accelerate the balanced binary search of the Gabow–Westermann p algorithm in order to obtain a runtime of (m3/2 log log p) for deter- O mining p, where m is the number of edges in the graph. A subgraph of density greater than d 1 can be determined within the same d ∗e − asymptotic runtime. In addition, the runtimes of several algorithms for determining p are compared experimentally. On current hardware, the computations can be carried out in minutes for social networks with hundreds of millions of edges. Building upon Kowalik’s approximation scheme, an approximation scheme for the arboricity with the same asymptotic runtime is devel- oped. In contrast to previous approaches, it does not only approximate the value of the arboricity, but also computes a corresponding forest partition. This is achieved using a fast conversion of k pseudoforests into k + 1 forests. Based on the concept of maximum density, a mixed integer linear program (MILP) can be formulated for finding a connected subgraph that minimizes a linear function. This problem, which is closely related to the Steiner tree problem on graphs, is NP-complete in general. For the case where the number of vertices is required to be exactly k, the MILP is compared to an existing formulation, the generalized subtour elimination constraints (GSEC), both in theory and in practice. Another topic under scrutiny is the approximation of the Steiner tree problem on graphs with the bidirected cut relaxation (BCR), which is equivalent to GSEC. It is shown that the algorithm of Byrka et al. computes a 1.354-approximation if the instances do not contain Steiner claws. Furthermore, an idea for generating hard instances is presented, yet it does not result in improved lower bounds on the integrality gap of BCR. v ACKNOWLEDGEMENTS First and foremost, I want to thank my advisor, Professor Ernst Alt- haus. He always had a friendly ear to my questions and valuable advice, and he let me freely pursue my interests in both research and teaching to a remarkable degree. I am also indebted to the supervisor of my three-month stay at the University of Waterloo in Canada, Professor Jochen Könemann. He took a lot of time to meet with me and discuss ideas, and invited me to a workshop at the Banff International Research Station. My colleagues at the Institute of Computer Science in Mainz also deserve credit for the wonderful working climate and the occasional get-together. I want to highlight the members of the Algorithmics group: Björn Beber, Domenico Mosca, Udo Muttray, and Sarah Ziegler, as well as ‘honorary member’ Frank Fischer. Last, but not least, I want to thank my wife Katharina for her support and our son Adrian, who fills both our lives with joy. vii CONTENTS 1 introduction1 1.1 Historical Background and Motivation . 1 1.2 Structure and Outline of the Thesis . 4 1.3 Collaboration and Publications . 6 2 preliminaries7 2.1 Basic Definitions . 7 2.1.1 Set-Theoretic Foundations . 7 2.1.2 Propositional Calculus . 8 2.2 Graphs . 9 2.2.1 Vertices and Edges . 9 2.2.2 Undirected and Simple Graphs . 10 2.2.3 Adjacency and Incidence . 10 2.2.4 Degrees and Orientations . 10 2.2.5 Subgraphs, Induced Subgraphs, and Matchings 11 2.2.6 Paths, Cycles, and Connected Components . 11 2.2.7 Trees and Planarity . 12 2.3 Asymptotics . 13 2.4 Probability Theory . 15 2.4.1 The Coupon Collector Problem . 17 2.5 Algorithms and Machine Models . 18 2.6 Complexity Classes . 19 2.7 Approximation Algorithms . 22 2.8 Breadth-First and Depth-First Search . 22 2.9 Linear Algebra . 24 2.10 Matroid Theory . 25 2.11 Linear Programming . 26 2.11.1 Linear Programs and the Canonical Form . 26 2.11.2 Polyhedra and Extreme Points . 27 2.11.3 Duality . 28 2.11.4 Total Unimodularity . 29 2.11.5 Algorithms to Solve Linear Programs . 30 2.11.6 Integer Linear Programs . 30 2.11.7 Branch-and-Bound and Branch-and-Cut . 32 2.12 The Maximum Flow Problem . 33 2.12.1 Flows as Linear Programs . 33 2.12.2 The Minimum Cut Problem . 35 2.12.3 Maximum Flows by Augmenting Paths . 36 2.12.4 Flow Algorithms and Their Runtimes . 39 2.13 Dinitz’s Algorithm . 40 2.14 Almost Unit Capacity Networks . 42 2.15 Dinitz’s Algorithm on AUC Networks . 44 ix x contents 3 the densest subgraph problem 47 3.1 Definition and Properties . 47 3.2 Bounds on the Maximum Density . 53 3.3 Algorithms for the Densest Subgraph Problem . 54 3.3.1 0-1 Fractional Programming . 54 3.3.2 The Provisioning Problem . 55 3.3.3 Goldberg’s Method . 56 3.4 Integral Test Values and Smaller Search Intervals . 60 3.5 Linear Programs for the Densest Subgraph Problem . 63 3.6 The Bipartite Orientation Network . 65 3.7 Streaming Algorithms . 73 4 the orientation problem 75 4.1 The Re-Orientation Algorithm . 75 4.2 Kowalik’s Approximation Scheme . 81 4.3 Applications and Generalizations . 84 5 balanced binary search 87 6 accelerated binary search 91 6.1 Fractional Orientations . 93 6.2 Bottleneck Maximum Cardinality Matching . 95 7 constant-factor approximations 97 7.1 The Greedy Algorithm . 97 7.2 The Algorithm of Asahiro et al. 99 7.3 Kowalik’s Scheme for Fixed e ............... 103 8 arboricity and pseudoarboricity 105 8.1 Forests and Pseudoforests . 105 8.2 Matroid Partitioning and Covering Numbers . 108 8.3 Runtimes for Computing the (Fractional) Arboricity . 114 8.4 Bounds for Arboricity and Pseudoarboricity . 116 9 conversion of pseudoforests into forests 121 9.1 Conversion by Divide-and-Conquer . 122 9.2 Linear-Time Conversions for Small k ........... 125 9.2.1 A Linear-Time 5/3-Conversion . 125 9.2.2 A Linear-Time 3/2-Conversion . 126 9.2.3 A Linear-Time 4/3-Conversion . 127 9.2.4 The Nine Dragon Tree Theorem . 133 9.2.5 An Application to Planar Graphs . 135 9.2.6 Partitioning a Planar Graph into Three Forests . 135 10 a constructive arboricity approximation scheme 137 10.1 The Surplus Graph . 137 10.2 Exchanging Edges on Cycles . 141 10.3 Finding the Exchange Edge . 143 11 preprocessing orientations 145 12 experimental comparisons for the orientation problem 149 12.1 Related Work . 149 12.2 Selection of Algorithms . 149 contents xi 12.3 LP Solver and Hardware Configuration . 151 12.4 Input Graphs . 151 12.5 Results . 152 13 problems involving connected subgraphs 157 14 the k-cardinality tree problem 159 14.1 Integer Linear Programs .
Load more

Recommended publications
  • Biased Graphs. Vii. Contrabalance and Antivoltages
    BIASED GRAPHS. VII. CONTRABALANCE AND ANTIVOLTAGES THOMAS ZASLAVSKY Abstract. We develop linear representation theory for bicircular matroids, a chief exam- ple being a matroid associated with forests of a graph, and bicircular lift matroids, a chief example being a matroid associated with spanning forests. (These are bias and lift matroids of contrabalanced biased graphs.) The theory is expressed largely in terms of antivoltages (edge labellings that defy Kirchhoff’s voltage law) with values in the multiplicative or ad- ditive group of the scalar field. We emphasize antivoltages with values in cyclic groups and finite vector spaces since they are crucial for representing the matroids over finite fields; and integer-valued antivoltages with bounded breadth since they are crucial in constructions. We find bounds for the existence of antivoltages and we solve some examples. Other results: The number of antivoltages in an abelian group is a polynomial function of the group order, and the number of integral antivoltages with bounded breadth is a polynomial in the breadth bound. We conclude with an application to complex representation. There are many open questions. Contents Introduction 2 1. Background 3 2. General bounds on representability and antivoltages 5 3. Modular, integral, and prime-power antivoltages 7 4. Minors and matroids 11 5. Completegraphsandcomplete-graphbounds 11 6. More examples 16 7. The number of antivoltages 18 8. Root-of-unity representations 21 References 21 Date: March 2001; Aug., 2002; Aug.–Sept., 2004; Nov.–Dec., 2005. Version of April 3, 2007. 2000 Mathematics Subject Classification. Primary 05B35, 05C22; Secondary 05A15, 05C35. Key words and phrases. Antivoltage, bicircular matroid, bicircular lift matroid, forest matroid, spanning forest matroid, biased graph, gain graph, contrabalance, bias matroid, frame matroid, matroid representation, transversal matroid.
    [Show full text]
  • Directed Graph Algorithms
    Directed Graph Algorithms CSE 373 Data Structures Readings • Reading Chapter 13 › Sections 13.3 and 13.4 Digraphs 2 Topological Sort 142 322 143 321 Problem: Find an order in which all these courses can 326 be taken. 370 341 Example: 142 Æ 143 Æ 378 Æ 370 Æ 321 Æ 341 Æ 322 Æ 326 Æ 421 Æ 401 378 421 In order to take a course, you must 401 take all of its prerequisites first Digraphs 3 Topological Sort Given a digraph G = (V, E), find a linear ordering of its vertices such that: for any edge (v, w) in E, v precedes w in the ordering B C A F D E Digraphs 4 Topo sort – valid solution B C Any linear ordering in which A all the arrows go to the right F is a valid solution D E A B F C D E Note that F can go anywhere in this list because it is not connected. Also the solution is not unique. Digraphs 5 Topo sort – invalid solution B C A Any linear ordering in which an arrow goes to the left F is not a valid solution D E A B F C E D NO! Digraphs 6 Paths and Cycles • Given a digraph G = (V,E), a path is a sequence of vertices v1,v2, …,vk such that: ›(vi,vi+1) in E for 1 < i < k › path length = number of edges in the path › path cost = sum of costs of each edge • A path is a cycle if : › k > 1; v1 = vk •G is acyclic if it has no cycles.
    [Show full text]
  • On Treewidth and Graph Minors
    On Treewidth and Graph Minors Daniel John Harvey Submitted in total fulfilment of the requirements of the degree of Doctor of Philosophy February 2014 Department of Mathematics and Statistics The University of Melbourne Produced on archival quality paper ii Abstract Both treewidth and the Hadwiger number are key graph parameters in structural and al- gorithmic graph theory, especially in the theory of graph minors. For example, treewidth demarcates the two major cases of the Robertson and Seymour proof of Wagner's Con- jecture. Also, the Hadwiger number is the key measure of the structural complexity of a graph. In this thesis, we shall investigate these parameters on some interesting classes of graphs. The treewidth of a graph defines, in some sense, how \tree-like" the graph is. Treewidth is a key parameter in the algorithmic field of fixed-parameter tractability. In particular, on classes of bounded treewidth, certain NP-Hard problems can be solved in polynomial time. In structural graph theory, treewidth is of key interest due to its part in the stronger form of Robertson and Seymour's Graph Minor Structure Theorem. A key fact is that the treewidth of a graph is tied to the size of its largest grid minor. In fact, treewidth is tied to a large number of other graph structural parameters, which this thesis thoroughly investigates. In doing so, some of the tying functions between these results are improved. This thesis also determines exactly the treewidth of the line graph of a complete graph. This is a critical example in a recent paper of Marx, and improves on a recent result by Grohe and Marx.
    [Show full text]
  • Graph Varieties Axiomatized by Semimedial, Medial, and Some Other Groupoid Identities
    Discussiones Mathematicae General Algebra and Applications 40 (2020) 143–157 doi:10.7151/dmgaa.1344 GRAPH VARIETIES AXIOMATIZED BY SEMIMEDIAL, MEDIAL, AND SOME OTHER GROUPOID IDENTITIES Erkko Lehtonen Technische Universit¨at Dresden Institut f¨ur Algebra 01062 Dresden, Germany e-mail: [email protected] and Chaowat Manyuen Department of Mathematics, Faculty of Science Khon Kaen University Khon Kaen 40002, Thailand e-mail: [email protected] Abstract Directed graphs without multiple edges can be represented as algebras of type (2, 0), so-called graph algebras. A graph is said to satisfy an identity if the corresponding graph algebra does, and the set of all graphs satisfying a set of identities is called a graph variety. We describe the graph varieties axiomatized by certain groupoid identities (medial, semimedial, autodis- tributive, commutative, idempotent, unipotent, zeropotent, alternative). Keywords: graph algebra, groupoid, identities, semimediality, mediality. 2010 Mathematics Subject Classification: 05C25, 03C05. 1. Introduction Graph algebras were introduced by Shallon [10] in 1979 with the purpose of providing examples of nonfinitely based finite algebras. Let us briefly recall this concept. Given a directed graph G = (V, E) without multiple edges, the graph algebra associated with G is the algebra A(G) = (V ∪ {∞}, ◦, ∞) of type (2, 0), 144 E. Lehtonen and C. Manyuen where ∞ is an element not belonging to V and the binary operation ◦ is defined by the rule u, if (u, v) ∈ E, u ◦ v := (∞, otherwise, for all u, v ∈ V ∪ {∞}. We will denote the product u ◦ v simply by juxtaposition uv. Using this representation, we may view any algebraic property of a graph algebra as a property of the graph with which it is associated.
    [Show full text]
  • Networkx: Network Analysis with Python
    NetworkX: Network Analysis with Python Salvatore Scellato Full tutorial presented at the XXX SunBelt Conference “NetworkX introduction: Hacking social networks using the Python programming language” by Aric Hagberg & Drew Conway Outline 1. Introduction to NetworkX 2. Getting started with Python and NetworkX 3. Basic network analysis 4. Writing your own code 5. You are ready for your project! 1. Introduction to NetworkX. Introduction to NetworkX - network analysis Vast amounts of network data are being generated and collected • Sociology: web pages, mobile phones, social networks • Technology: Internet routers, vehicular flows, power grids How can we analyze this networks? Introduction to NetworkX - Python awesomeness Introduction to NetworkX “Python package for the creation, manipulation and study of the structure, dynamics and functions of complex networks.” • Data structures for representing many types of networks, or graphs • Nodes can be any (hashable) Python object, edges can contain arbitrary data • Flexibility ideal for representing networks found in many different fields • Easy to install on multiple platforms • Online up-to-date documentation • First public release in April 2005 Introduction to NetworkX - design requirements • Tool to study the structure and dynamics of social, biological, and infrastructure networks • Ease-of-use and rapid development in a collaborative, multidisciplinary environment • Easy to learn, easy to teach • Open-source tool base that can easily grow in a multidisciplinary environment with non-expert users
    [Show full text]
  • Counting Independent Sets in Graphs with Bounded Bipartite Pathwidth∗
    Counting independent sets in graphs with bounded bipartite pathwidth∗ Martin Dyery Catherine Greenhillz School of Computing School of Mathematics and Statistics University of Leeds UNSW Sydney, NSW 2052 Leeds LS2 9JT, UK Australia [email protected] [email protected] Haiko M¨uller∗ School of Computing University of Leeds Leeds LS2 9JT, UK [email protected] 7 August 2019 Abstract We show that a simple Markov chain, the Glauber dynamics, can efficiently sample independent sets almost uniformly at random in polynomial time for graphs in a certain class. The class is determined by boundedness of a new graph parameter called bipartite pathwidth. This result, which we prove for the more general hardcore distribution with fugacity λ, can be viewed as a strong generalisation of Jerrum and Sinclair's work on approximately counting matchings, that is, independent sets in line graphs. The class of graphs with bounded bipartite pathwidth includes claw-free graphs, which generalise line graphs. We consider two further generalisations of claw-free graphs and prove that these classes have bounded bipartite pathwidth. We also show how to extend all our results to polynomially-bounded vertex weights. 1 Introduction There is a well-known bijection between matchings of a graph G and independent sets in the line graph of G. We will show that we can approximate the number of independent sets ∗A preliminary version of this paper appeared as [19]. yResearch supported by EPSRC grant EP/S016562/1 \Sampling in hereditary classes". zResearch supported by Australian Research Council grant DP190100977. 1 in graphs for which all bipartite induced subgraphs are well structured, in a sense that we will define precisely.
    [Show full text]
  • Linear K-Arboricities on Trees
    Discrete Applied Mathematics 103 (2000) 281–287 View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Note Linear k-arboricities on trees Gerard J. Changa; 1, Bor-Liang Chenb, Hung-Lin Fua, Kuo-Ching Huangc; ∗;2 aDepartment of Applied Mathematics, National Chiao Tung University, Hsinchu 300, Taiwan bDepartment of Business Administration, National Taichung Institue of Commerce, Taichung 404, Taiwan cDepartment of Applied Mathematics, Providence University, Shalu 433, Taichung, Taiwan Received 31 October 1997; revised 15 November 1999; accepted 22 November 1999 Abstract For a ÿxed positive integer k, the linear k-arboricity lak (G) of a graph G is the minimum number ‘ such that the edge set E(G) can be partitioned into ‘ disjoint sets and that each induces a subgraph whose components are paths of lengths at most k. This paper studies linear k-arboricity from an algorithmic point of view. In particular, we present a linear-time algo- rithm to determine whether a tree T has lak (T)6m. ? 2000 Elsevier Science B.V. All rights reserved. Keywords: Linear forest; Linear k-forest; Linear arboricity; Linear k-arboricity; Tree; Leaf; Penultimate vertex; Algorithm; NP-complete 1. Introduction All graphs in this paper are simple, i.e., ÿnite, undirected, loopless, and without multiple edges. A linear k-forest is a graph whose components are paths of length at most k.Alinear k-forest partition of G is a partition of the edge set E(G) into linear k-forests. The linear k-arboricity of G, denoted by lak (G), is the minimum size of a linear k-forest partition of G.
    [Show full text]
  • Interval Edge-Colorings of Graphs
    University of Central Florida STARS Electronic Theses and Dissertations, 2004-2019 2016 Interval Edge-Colorings of Graphs Austin Foster University of Central Florida Part of the Mathematics Commons Find similar works at: https://stars.library.ucf.edu/etd University of Central Florida Libraries http://library.ucf.edu This Masters Thesis (Open Access) is brought to you for free and open access by STARS. It has been accepted for inclusion in Electronic Theses and Dissertations, 2004-2019 by an authorized administrator of STARS. For more information, please contact [email protected]. STARS Citation Foster, Austin, "Interval Edge-Colorings of Graphs" (2016). Electronic Theses and Dissertations, 2004-2019. 5133. https://stars.library.ucf.edu/etd/5133 INTERVAL EDGE-COLORINGS OF GRAPHS by AUSTIN JAMES FOSTER B.S. University of Central Florida, 2015 A thesis submitted in partial fulfilment of the requirements for the degree of Master of Science in the Department of Mathematics in the College of Sciences at the University of Central Florida Orlando, Florida Summer Term 2016 Major Professor: Zixia Song ABSTRACT A proper edge-coloring of a graph G by positive integers is called an interval edge-coloring if the colors assigned to the edges incident to any vertex in G are consecutive (i.e., those colors form an interval of integers). The notion of interval edge-colorings was first introduced by Asratian and Kamalian in 1987, motivated by the problem of finding compact school timetables. In 1992, Hansen described another scenario using interval edge-colorings to schedule parent-teacher con- ferences so that every person’s conferences occur in consecutive slots.
    [Show full text]
  • Network Analysis of the Multimodal Freight Transportation System in New York City
    Network Analysis of the Multimodal Freight Transportation System in New York City Project Number: 15 – 2.1b Year: 2015 FINAL REPORT June 2018 Principal Investigator Qian Wang Researcher Shuai Tang MetroFreight Center of Excellence University at Buffalo Buffalo, NY 14260-4300 Network Analysis of the Multimodal Freight Transportation System in New York City ABSTRACT The research is aimed at examining the multimodal freight transportation network in the New York metropolitan region to identify critical links, nodes and terminals that affect last-mile deliveries. Two types of analysis were conducted to gain a big picture of the region’s freight transportation network. First, three categories of network measures were generated for the highway network that carries the majority of last-mile deliveries. They are the descriptive measures that demonstrate the basic characteristics of the highway network, the network structure measures that quantify the connectivity of nodes and links, and the accessibility indices that measure the ease to access freight demand, services and activities. Second, 71 multimodal freight terminals were selected and evaluated in terms of their accessibility to major multimodal freight demand generators such as warehousing establishments. As found, the most important highways nodes that are critical in terms of connectivity and accessibility are those in and around Manhattan, particularly the bridges and tunnels connecting Manhattan to neighboring areas. Major multimodal freight demand generators, such as warehousing establishments, have better accessibility to railroad and marine port terminals than air and truck terminals in general. The network measures and findings in the research can be used to understand the inventory of the freight network in the system and to conduct freight travel demand forecasting analysis.
    [Show full text]
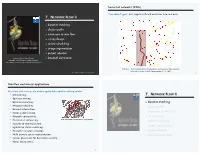
  • 7. NETWORK FLOW II ‣ Bipartite Matching ‣ Disjoint Paths
    Soviet rail network (1950s) "Free world" goal. Cut supplies (if cold war turns into real war). 7. NETWORK FLOW II ‣ bipartite matching ‣ disjoint paths ‣ extensions to max flow ‣ survey design ‣ airline scheduling ‣ image segmentation ‣ project selection Lecture slides by Kevin Wayne ‣ baseball elimination Copyright © 2005 Pearson-Addison Wesley http://www.cs.princeton.edu/~wayne/kleinberg-tardos Reference: On the history of the transportation and maximum flow problems. Alexander Schrijver in Math Programming, 91: 3, 2002. Last updated on Mar 31, 2013 3:25 PM Figure 2 2 From Harris and Ross [1955]: Schematic diagram of the railway network of the Western So- viet Union and Eastern European countries, with a maximum flow of value 163,000 tons from Russia to Eastern Europe, and a cut of capacity 163,000 tons indicated as ‘The bottleneck’. Max-flow and min-cut applications Max-flow and min-cut are widely applicable problem-solving model. ・Data mining. 7. NETWORK FLOW II ・Open-pit mining. ・Bipartite matching. ‣ bipartite matching ・Network reliability. ‣ disjoint paths ・Baseball elimination. ‣ extensions to max flow ・Image segmentation. ・Network connectivity. ‣ survey design liver and hepatic vascularization segmentation ・Distributed computing. ‣ airline scheduling ・Security of statistical data. ‣ image segmentation ・Egalitarian stable matching. ・Network intrusion detection. ‣ project selection ・Multi-camera scene reconstruction. ‣ baseball elimination ・Sensor placement for homeland security. ・Many, many, more. 3 Matching Bipartite matching Def. Given an undirected graph G = (V, E) a subset of edges M ⊆ E is Def. A graph G is bipartite if the nodes can be partitioned into two subsets a matching if each node appears in at most one edge in M.
    [Show full text]
  • David Gries, 2018 Graph Coloring A
    Graph coloring A coloring of an undirected graph is an assignment of a color to each node so that adja- cent nodes have different colors. The graph to the right, taken from Wikipedia, is known as the Petersen graph, after Julius Petersen, who discussed some of its properties in 1898. It has been colored with 3 colors. It can’t be colored with one or two. The Petersen graph has both K5 and bipartite graph K3,3, so it is not planar. That’s all you have to know about the Petersen graph. But if you are at all interested in what mathemati- cians and computer scientists do, visit the Wikipedia page for Petersen graph. This discussion on graph coloring is important not so much for what it says about the four-color theorem but what it says about proofs by computers, for the proof of the four-color theorem was just about the first one to use a computer and sparked a lot of controversy. Kempe’s flawed proof that four colors suffice to color a planar graph Thoughts about graph coloring appear to have sprung up in England around 1850 when people attempted to color maps, which can be represented by planar graphs in which the nodes are countries and adjacent countries have a directed edge between them. Francis Guthrie conjectured that four colors would suffice. In 1879, Alfred Kemp, a barrister in London, published a proof in the American Journal of Mathematics that only four colors were needed to color a planar graph. Eleven years later, P.J.
    [Show full text]
  • Models for Networks with Consumable Resources: Applications to Smart Cities Hayato Montezuma Ushijima-Mwesigwa Clemson University, [email protected]
    Clemson University TigerPrints All Dissertations Dissertations 12-2018 Models for Networks with Consumable Resources: Applications to Smart Cities Hayato Montezuma Ushijima-Mwesigwa Clemson University, [email protected] Follow this and additional works at: https://tigerprints.clemson.edu/all_dissertations Recommended Citation Ushijima-Mwesigwa, Hayato Montezuma, "Models for Networks with Consumable Resources: Applications to Smart Cities" (2018). All Dissertations. 2284. https://tigerprints.clemson.edu/all_dissertations/2284 This Dissertation is brought to you for free and open access by the Dissertations at TigerPrints. It has been accepted for inclusion in All Dissertations by an authorized administrator of TigerPrints. For more information, please contact [email protected]. Models for Networks with Consumable Resources: Applications to Smart Cities A Dissertation Presented to the Graduate School of Clemson University In Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy Computer Science by Hayato Ushijima-Mwesigwa December 2018 Accepted by: Dr. Ilya Safro, Committee Chair Dr. Mashrur Chowdhury Dr. Brian Dean Dr. Feng Luo Abstract In this dissertation, we introduce different models for understanding and controlling the spreading dynamics of a network with a consumable resource. In particular, we consider a spreading process where a resource necessary for transit is partially consumed along the way while being refilled at special nodes on the network. Examples include fuel consumption of vehicles together with refueling stations, information loss during dissemination with error correcting nodes, consumption of ammunition of military troops while moving, and migration of wild animals in a network with a limited number of water-holes. We undertake this study from two different perspectives. First, we consider a network science perspective where we are interested in identifying the influential nodes, and estimating a nodes’ relative spreading influence in the network.
    [Show full text]