Construction and Box Dimension of Recurrent Fractal Interpolation Surfaces
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Pour Une Analyse Comparée De La Didactique Du Chinois LE
THÈSE Pour obtenir le grade de DOCTEUR DE L’UNIVERSITE GRENOBLE ALPES préparée dans le cadre d’une cotutelle entre la Communauté Université Grenoble Alpes et l’Università Ca’ Foscari Venezia Spécialité : Didactique et Linguistique Arrêté ministériel : le 6 janvier 2005 – 25 mai 2016 Présentée par Tommaso ROSSI Thèse codirigée par Mariarosaria GIANNINOTO et Franco GATTI préparée au sein du Laboratoire LIDILEM et du Département DSAAM dans les Écoles Doctorales «Langues Littératures et Sciences Humaines» et «Studi sull’Asia e sull’Africa» Pour une analyse comparée de la didactique du chinois LE Une étude exploratoire des approches méthodologiques, des stratégies didactiques et des matériaux pédagogiques en Italie et en France Thèse soutenue publiquement le 19 mars 2021, devant le jury composé de : M.me Clara BULFONI Professeur à l’Università degli Studi di Milano, Présidente M. Franco GATTI Professeur à l’Università Ca’ Foscari Venezia, Co-directeur/Membre M.me Mariarosaria GIANNINOTO Professeur à l’Université Paul Valéry Montpellier, Co-directrice/Membre M.me Carlotta SPARVOLI Professeur à l’Università di Bologna, Rapporteuse M. Alain PEYRAUBE Directeur de recherche émérite au CRLAO, Rapporteur M.me Marinette MATTHEY Professeur à l’Université Grenoble-Alpes, Membre Table of contents ABSTRACT (ENGLISH VERSION) ........................................................ 9 RÉSUMÉ (VERSION FRANÇAISE) ..................................................... 11 INTRODUCTION .................................................................................... -
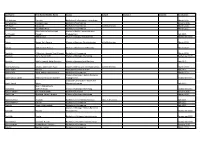
Last Name First Name/Middle Name Course Award Course 2 Award 2 Graduation
Last Name First Name/Middle Name Course Award Course 2 Award 2 Graduation A/L Krishnan Thiinash Bachelor of Information Technology March 2015 A/L Selvaraju Theeban Raju Bachelor of Commerce January 2015 A/P Balan Durgarani Bachelor of Commerce with Distinction March 2015 A/P Rajaram Koushalya Priya Bachelor of Commerce March 2015 Hiba Mohsin Mohammed Master of Health Leadership and Aal-Yaseen Hussein Management July 2015 Aamer Muhammad Master of Quality Management September 2015 Abbas Hanaa Safy Seyam Master of Business Administration with Distinction March 2015 Abbasi Muhammad Hamza Master of International Business March 2015 Abdallah AlMustafa Hussein Saad Elsayed Bachelor of Commerce March 2015 Abdallah Asma Samir Lutfi Master of Strategic Marketing September 2015 Abdallah Moh'd Jawdat Abdel Rahman Master of International Business July 2015 AbdelAaty Mosa Amany Abdelkader Saad Master of Media and Communications with Distinction March 2015 Abdel-Karim Mervat Graduate Diploma in TESOL July 2015 Abdelmalik Mark Maher Abdelmesseh Bachelor of Commerce March 2015 Master of Strategic Human Resource Abdelrahman Abdo Mohammed Talat Abdelziz Management September 2015 Graduate Certificate in Health and Abdel-Sayed Mario Physical Education July 2015 Sherif Ahmed Fathy AbdRabou Abdelmohsen Master of Strategic Marketing September 2015 Abdul Hakeem Siti Fatimah Binte Bachelor of Science January 2015 Abdul Haq Shaddad Yousef Ibrahim Master of Strategic Marketing March 2015 Abdul Rahman Al Jabier Bachelor of Engineering Honours Class II, Division 1 -

Regulating SARS in China: Law As an Antidote?
Washington University Global Studies Law Review Volume 4 Issue 1 January 2005 Regulating SARS in China: Law As an Antidote? Chenglin Liu St. Mary's University Follow this and additional works at: https://openscholarship.wustl.edu/law_globalstudies Part of the Comparative and Foreign Law Commons, and the Health Law and Policy Commons Recommended Citation Chenglin Liu, Regulating SARS in China: Law As an Antidote?, 4 WASH. U. GLOBAL STUD. L. REV. 81 (2005), https://openscholarship.wustl.edu/law_globalstudies/vol4/iss1/4 This Article is brought to you for free and open access by the Law School at Washington University Open Scholarship. It has been accepted for inclusion in Washington University Global Studies Law Review by an authorized administrator of Washington University Open Scholarship. For more information, please contact [email protected]. REGULATING SARS IN CHINA: LAW AS AN ANTIDOTE? CHENGLIN LIU* I. INTRODUCTION ...................................................................................... 82 II. THE DEVELOPMENT OF THE SARS EPIDEMIC BEFORE APRIL 20, 2003 ........................................................................................... 84 A. Starting from Guangdong.......................................................... 84 B. From Guangdong to Hong Kong and the Rest of the World..... 86 C. Entering Beijing ........................................................................ 87 III. FIGHTING TO RELEASE SARS INFORMATION: AN UPHILL BATTLE... 89 IV. NEW GOVERNMENT AND NEW APPROACH........................................ -

Jing Chen, Xi Huo, and Shigui Ruan Proposal of Organizing A
Disease Modelling – from Within-Host to Population Organizers: Jing Chen, Xi Huo, and Shigui Ruan Proposal of organizing a mini-symposium in CMPD5 • Mini-symposium title: Disease Modelling – from Within-Host to Population • Organizers: Jing Chen, Nova Southeastern University, [email protected] Xi Huo, University of Miami, [email protected] Shigui Ruan, University of Miami, [email protected] • Synopsis: The scope of disease models varies with respect to the purpose of the study, from the within-host scale on the dynamics of cells and pathogens, to the population scale on the dynamics of human and vector populations. This mini-symposium brings together talks in different scales of disease modeling, and aims for stimulating ideas and collaborations in multiple-scale modelling. The invited talks are nicely balanced in both scales: we will have talks given by Drs. Gurarie (1st talk), Jang, Munther, Rong, Salceanu, focusing on the dynamics of the pathogens and immune cells within the host population. We have Dr. Vaidya talking about how to bridge within-host and between host dynamics together in order to model HIV infections and spreads. We will have another half of speakers, Drs. Deng, Feng, Gurarie (2nd talk), Huang, Nevai, Ripoll, Shuai, and Zhang, to talk about modeling transmission and control of various diseases on the population level. Lastly, we will have Hao Kang to present his findings in analyzing a generalized structured population model on disease spreads. • Confirmed speakers: 1. Libin Rong, University of Florida Title: Modeling HIV Dynamics under Treatment 2. Paul Salceanu, University of Louisiana at Lafayette Title: A Time-Delay Bacteria and Chronic Bacteriophage Model 3. -

Representing Talented Women in Eighteenth-Century Chinese Painting: Thirteen Female Disciples Seeking Instruction at the Lake Pavilion
REPRESENTING TALENTED WOMEN IN EIGHTEENTH-CENTURY CHINESE PAINTING: THIRTEEN FEMALE DISCIPLES SEEKING INSTRUCTION AT THE LAKE PAVILION By Copyright 2016 Janet C. Chen Submitted to the graduate degree program in Art History and the Graduate Faculty of the University of Kansas in partial fulfillment of the requirements for the degree of Doctor of Philosophy. ________________________________ Chairperson Marsha Haufler ________________________________ Amy McNair ________________________________ Sherry Fowler ________________________________ Jungsil Jenny Lee ________________________________ Keith McMahon Date Defended: May 13, 2016 The Dissertation Committee for Janet C. Chen certifies that this is the approved version of the following dissertation: REPRESENTING TALENTED WOMEN IN EIGHTEENTH-CENTURY CHINESE PAINTING: THIRTEEN FEMALE DISCIPLES SEEKING INSTRUCTION AT THE LAKE PAVILION ________________________________ Chairperson Marsha Haufler Date approved: May 13, 2016 ii Abstract As the first comprehensive art-historical study of the Qing poet Yuan Mei (1716–97) and the female intellectuals in his circle, this dissertation examines the depictions of these women in an eighteenth-century handscroll, Thirteen Female Disciples Seeking Instructions at the Lake Pavilion, related paintings, and the accompanying inscriptions. Created when an increasing number of women turned to the scholarly arts, in particular painting and poetry, these paintings documented the more receptive attitude of literati toward talented women and their support in the social and artistic lives of female intellectuals. These pictures show the women cultivating themselves through literati activities and poetic meditation in nature or gardens, common tropes in portraits of male scholars. The predominantly male patrons, painters, and colophon authors all took part in the formation of the women’s public identities as poets and artists; the first two determined the visual representations, and the third, through writings, confirmed and elaborated on the designated identities. -

Names of Chinese People in Singapore
101 Lodz Papers in Pragmatics 7.1 (2011): 101-133 DOI: 10.2478/v10016-011-0005-6 Lee Cher Leng Department of Chinese Studies, National University of Singapore ETHNOGRAPHY OF SINGAPORE CHINESE NAMES: RACE, RELIGION, AND REPRESENTATION Abstract Singapore Chinese is part of the Chinese Diaspora.This research shows how Singapore Chinese names reflect the Chinese naming tradition of surnames and generation names, as well as Straits Chinese influence. The names also reflect the beliefs and religion of Singapore Chinese. More significantly, a change of identity and representation is reflected in the names of earlier settlers and Singapore Chinese today. This paper aims to show the general naming traditions of Chinese in Singapore as well as a change in ideology and trends due to globalization. Keywords Singapore, Chinese, names, identity, beliefs, globalization. 1. Introduction When parents choose a name for a child, the name necessarily reflects their thoughts and aspirations with regards to the child. These thoughts and aspirations are shaped by the historical, social, cultural or spiritual setting of the time and place they are living in whether or not they are aware of them. Thus, the study of names is an important window through which one could view how these parents prefer their children to be perceived by society at large, according to the identities, roles, values, hierarchies or expectations constructed within a social space. Goodenough explains this culturally driven context of names and naming practices: Department of Chinese Studies, National University of Singapore The Shaw Foundation Building, Block AS7, Level 5 5 Arts Link, Singapore 117570 e-mail: [email protected] 102 Lee Cher Leng Ethnography of Singapore Chinese Names: Race, Religion, and Representation Different naming and address customs necessarily select different things about the self for communication and consequent emphasis. -

CHSA HP2010.Pdf
The Hawai‘i Chinese: Their Experience and Identity Over Two Centuries 2 0 1 0 CHINESE AMERICA History&Perspectives thej O u r n a l O f T HE C H I n E s E H I s T O r I C a l s OCIET y O f a m E r I C a Chinese America History and PersPectives the Journal of the chinese Historical society of america 2010 Special issUe The hawai‘i Chinese Chinese Historical society of america with UCLA asian american studies center Chinese America: History & Perspectives – The Journal of the Chinese Historical Society of America The Hawai‘i Chinese chinese Historical society of america museum & learning center 965 clay street san francisco, california 94108 chsa.org copyright © 2010 chinese Historical society of america. all rights reserved. copyright of individual articles remains with the author(s). design by side By side studios, san francisco. Permission is granted for reproducing up to fifty copies of any one article for educa- tional Use as defined by thed igital millennium copyright act. to order additional copies or inquire about large-order discounts, see order form at back or email [email protected]. articles appearing in this journal are indexed in Historical Abstracts and America: History and Life. about the cover image: Hawai‘i chinese student alliance. courtesy of douglas d. l. chong. Contents Preface v Franklin Ng introdUction 1 the Hawai‘i chinese: their experience and identity over two centuries David Y. H. Wu and Harry J. Lamley Hawai‘i’s nam long 13 their Background and identity as a Zhongshan subgroup Douglas D. -

Communication, Empire, and Authority in the Qing Gazette
COMMUNICATION, EMPIRE, AND AUTHORITY IN THE QING GAZETTE by Emily Carr Mokros A dissertation submitted to Johns Hopkins University in conformity with the requirements for the degree of Doctor of Philosophy Baltimore, Maryland June, 2016 © 2016 Emily Carr Mokros All rights Reserved Abstract This dissertation studies the political and cultural roles of official information and political news in late imperial China. Using a wide-ranging selection of archival, library, and digitized sources from libraries and archives in East Asia, Europe, and the United States, this project investigates the production, regulation, and reading of the Peking Gazette (dibao, jingbao), a distinctive communications channel and news publication of the Qing Empire (1644-1912). Although court gazettes were composed of official documents and communications, the Qing state frequently contracted with commercial copyists and printers in publishing and distributing them. As this dissertation shows, even as the Qing state viewed information control and dissemination as a strategic concern, it also permitted the free circulation of a huge variety of timely political news. Readers including both officials and non-officials used the gazette in order to compare judicial rulings, assess military campaigns, and follow court politics and scandals. As the first full-length study of the Qing gazette, this project shows concretely that the gazette was a powerful factor in late imperial Chinese politics and culture, and analyzes the close relationship between information and imperial practice in the Qing Empire. By arguing that the ubiquitous gazette was the most important link between the Qing state and the densely connected information society of late imperial China, this project overturns assumptions that underestimate the importance of court gazettes and the extent of popular interest in political news in Chinese history. -

Phase-Field Simulation of Polymer Crystallization During Cooling Stage
International Journal of Chemical Engineering and Applications, Vol. 6, No. 1, February 2015 Phase-Field Simulation of Polymer Crystallization during Cooling Stage Xiaodong Wang and Jie Ouyang and growth, in order to perform cross-scale simulation on Abstract—The phase-field method has been developed to envelop profiles of the domain and the internal structure of simulate the crystal growth of semi-crystalline polymer during spherulites. Ruan et al. [4] proposed a pixel coloring cooling stage by considering the effect of temperature on the technique based on the Hoffman-Lauritzen theory to capture nucleation density. It assumes that the nucleation mechanism is heterogeneous, and the relationship between the nucleation the crystallization morphology evolution and calculating the density and the temperature is described by an empirical crystallization kinetics. According to coupling the function. The crystal growth after nucleation is modeled by a temperature field, non-isothermal crystallizations of polymers modified phase-field method which uses a non-conserved crystal with or without short fiber reinforced components were order parameter to indicate whether the material is solid or simulated. liquid. By using the proposed model, the influence of cooling Except the above mentioned approaches, the phase-field rate on the crystallization morphologies and crystallization kinetics has been investigated. methods can also be used to model the crystallization morphologies of semi-crystalline polymers [5]-[9]. This kind Index Terms—Polymer, crystallization, phase-field, cooling. of method has been successfully applied to simulate the polycrystalline growth of polymers and reveal the corresponding formation mechanisms under isothermal I. INTRODUCTION conditions. However, for the crystallizations under It is well known that polymer is one of the most important non-isothermal conditions, the phase-field methods have not technical materials in our daily life. -

XIULIN RUAN Curriculum Vita (As of 5/1/2020)
XIULIN RUAN Curriculum Vita (as of 5/1/2020) Residence: University: 3636 Hamilton St Mechanical Engineering, Purdue University West Lafayette, IN 47906 585 Purdue Mall, West Lafayette, IN 47907 (765)426-0658 (765)494-5721 E-mail: [email protected] URL: https://engineering.purdue.edu/ME/People/ptProfile?id=29343 Table of Contents Education .............................................................................................................................................................................. 1 Professional Appointments ................................................................................................................................................... 1 Visiting Positions .................................................................................................................................................................. 1 Research Interests ................................................................................................................................................................. 2 Honors and Awards .............................................................................................................................................................. 2 Journal Publications .............................................................................................................................................................. 2 Refereed Conference Papers (including 4 invited papers) ................................................................................................... -

The Exploitation of Big Data Technologies in Chinese Retail
Master’s Degree Programme In Languages, Economics and Institutions of Asia and North Africa “Second Cycle (D.M.) 270/2004” Final Thesis The Exploitation of Big Data Technologies in Chinese Retail Towards the Creation of a Regulatory Framework for Privacy Protection. Supervisor Ch. Prof. Renzo Riccardo Cavalieri Assistant supervisor PhD Student Diego Todaro Graduand Federica Stortoni Matriculation number 856935 Academic Year 2019 / 2020 前言 过去 30 年中,数字技术的发展导致数据和信息社会的相关性以及在线信息的可用 性不断提高。该网络构成了一个新的数据矿山(无论是个人数据还是其他数据),它 们的提取可以创造价值和新的知识水平。恰恰是处理个人数据的现代技术可以实现公 共和私人参与者的上述目标。一方面,数据处理在信息社会的发展中起着关键作用; 另一方面,它对保护隐私和个人数据提出了复杂的挑战。讨论的主题是大数据现象。 这项工作旨在分析应用于中国零售业的大数据现象对保护消费者的隐私和个人数 据带来的挑战,之前确定了可以突出现象主要特征的大数据定义并关注特别是关于通 过大数据分析技术进行数据处理的作用。 投资中国零售业的数字革命是史无前例的:2013 年,中国电子商务在规模和利润 方面均已超过美国,但仍保持着世界纪录。中国电子商务生态系统是一个创新孵化器。 多年来,由于智能手机、电子支付和面部识别支付、二维码的出现,以及包括 KOL 和 KOC 在内的新影响力者的诞生,它对传统的购买方式进行了许多改变,如移动商务的发 展。 对于中国消费者而言,零售领域的创新也在发生:他们不再只从零售商那里寻求实 质性产品,而是希望拥有一种既能娱乐又有趣的体验,并能增加购买过程的价值。这 种新现象由阿里巴巴创始人马云(Jack Ma)定义,名称为“ Entertainmerce”,对公 司而言意味着对营销和与客户沟通技术的改变。实际上,零售商必须根据消费者需求 调整报价,根据每个人的喜好和口味定制产品。通过这种方式,可以更改其业务方法, 从而为生产和产品沟通创建“以客户为中心”的模型。 本文的第一章着重分析了中国零售界发生的技术变革。提供其当前特征的概述,并 描述从简单的客户到公司生产和决策过程不可或缺的部分,消费者角色的转变。此外, 我还将在本章中强调技术领域的三大巨头(百度,阿里巴巴,腾讯)在中国经济中的 作用:由于使用了分析技术,这三家公司有机会充分了解客户的消费历程,并能够实 时利用各种接触点上可用的大量信息,例如社交媒体,物联网,电子商务平台等。 1 大数据代表零售业的未来,要在这个不断发展的数字现实中生存并取得成功,再加上 人工智能的使用,改变了中国零售业的世界,使阿里巴巴,百度和腾讯等公司成为了 零售业的领导者。由于其庞大的注册用户数量,每日流量和交易量,其行业严重依赖 于消费者的个人数据来开发量身定制的创新服务,并跻身全球十大互联网公司之列。 我将特别描述腾讯微信社交平台的现象。实际上,这标志着“多合一应用程序”系统 的出现,成为一种数字超级应用程序,用户可以在不离开该应用程序的情况下进行各 种活动。这个新系统令人担忧的方面是,无数用户数据和信息集中在一家公司手中, -

Surname Methodology in Defining Ethnic Populations : Chinese
Surname Methodology in Defining Ethnic Populations: Chinese Canadians Ethnic Surveillance Series #1 August, 2005 Surveillance Methodology, Health Surveillance, Public Health Division, Alberta Health and Wellness For more information contact: Health Surveillance Alberta Health and Wellness 24th Floor, TELUS Plaza North Tower P.O. Box 1360 10025 Jasper Avenue, STN Main Edmonton, Alberta T5J 2N3 Phone: (780) 427-4518 Fax: (780) 427-1470 Website: www.health.gov.ab.ca ISBN (on-line PDF version): 0-7785-3471-5 Acknowledgements This report was written by Dr. Hude Quan, University of Calgary Dr. Donald Schopflocher, Alberta Health and Wellness Dr. Fu-Lin Wang, Alberta Health and Wellness (Authors are ordered by alphabetic order of surname). The authors gratefully acknowledge the surname review panel members of Thu Ha Nguyen and Siu Yu, and valuable comments from Yan Jin and Shaun Malo of Alberta Health & Wellness. They also thank Dr. Carolyn De Coster who helped with the writing and editing of the report. Thanks to Fraser Noseworthy for assisting with the cover page design. i EXECUTIVE SUMMARY A Chinese surname list to define Chinese ethnicity was developed through literature review, a panel review, and a telephone survey of a randomly selected sample in Calgary. It was validated with the Canadian Community Health Survey (CCHS). Results show that the proportion who self-reported as Chinese has high agreement with the proportion identified by the surname list in the CCHS. The surname list was applied to the Alberta Health Insurance Plan registry database to define the Chinese ethnic population, and to the Vital Statistics Death Registry to assess the Chinese ethnic population mortality in Alberta.