Real-Time Fault Detection and Situational Awareness for Rovers: Report on the Mars Technology Program Task
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Refactoring the Curiosity Rover's Sample Handling Architecture on Mars
Refactoring the Curiosity Rover's Sample Handling Architecture on Mars Vandi Verma Stephen Kuhn (abstracting the shared development effort of many) The research was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. Copyright 2018 California Institute of Technology. U.S. Government sponsorship acknowledged. Introduction • The Mars Science Laboratory (“MSL”) hardware was architected to enable a fixed progression of activities that essentially enforced a campaign structure. In this structure, sample processing and analysis conflicted with any other usage of the robotic arm. • Unable to stow the arm and drive away • Unable to deploy arm instruments for in-situ engineering or science • Unable to deploy arm instruments or mechanisms on new targets • Sampling engineers developed and evolved a refactoring of this architecture in order to have it both ways Turn the hardware into a series of caches and catchments that could service all arm orientations. Enable execution of other arm activities with one “active” sample Page 2 11/18/20preserved such that additional portions could be delivered. The Foundational Risk Page 3 11/18/20 The Original Approach Page 4 11/18/20 Underpinnings of the original approach • Fundamentally, human rover planners simply could not keep track of sample in CHIMRA as it sluiced, stick- slipped, fell over partitions, pooled in catchments, etc. Neither could we update the Flight Software to model this directly. • But, with some simplifying abstraction of sample state and preparation of it into confined regimes of orientation, ground tools could effectively track sample. Rover planners’ use of Software Simulator was extended to enforce a chain of custody in commanded orientation, creating a faulted breakpoint upon violation that could be used to fix it. -

(PLEXIL) for Executable Plans and Command Sequences”, International Symposium on Artificial Intelligence, Robotics and Automation in Space (Isairas), 2005
V. Verma, T. Estlin, A. Jónsson, C. Pasareanu, R. Simmons, K. Tso, “Plan Execution Interchange Language (PLEXIL) for Executable Plans and Command Sequences”, International Symposium on Artificial Intelligence, Robotics and Automation in Space (iSAIRAS), 2005 PLAN EXECUTION INTERCHANGE LANGUAGE (PLEXIL) FOR EXECUTABLE PLANS AND COMMAND SEQUENCES Vandi Verma(1), Tara Estlin(2), Ari Jónsson(3), Corina Pasareanu(4), Reid Simmons(5), Kam Tso(6) (1)QSS Inc. at NASA Ames Research Center, MS 269-1 Moffett Field CA 94035, USA, Email:[email protected] (2)Jet Propulsion Laboratory, M/S 126-347, 4800 Oak Grove Drive, Pasadena CA 9110, USA , Email:[email protected] (3) USRA-RIACS at NASA Ames Research Center, MS 269-1 Moffett Field CA 94035, USA, Email:[email protected] (4)QSS Inc. at NASA Ames Research Center, MS 269-1 Moffett Field CA 94035, USA, Email:[email protected] (5)Robotics Institute, Carnegie Mellon University, Pittsburgh PA 15213, USA, Email:[email protected] (6)IA Tech Inc., 10501Kinnard Avenue, Los Angeles, CA 9002, USA, Email: [email protected] ABSTRACT this task since it is impossible for a small team to manually keep track of all sub-systems in real time. Space mission operations require flexible, efficient and Complex manipulators and instruments used in human reliable plan execution. In typical operations command missions must also execute sequences of commands to sequences (which are a simple subset of general perform complex tasks. Similarly, a rover operating on executable plans) are generated on the ground, either Mars must autonomously execute commands sent from manually or with assistance from automated planning, Earth and keep the rover safe in abnormal situations. -

Enabling and Enhancing Astrophysical Observations with Autonomous Systems
Enabling and Enhancing Astrophysical Observations with Autonomous Systems Rashied Amini1;a, Steve Chien1, Lorraine Fesq1, Jeremy Frank2 , Ksenia Kolcio3, Bertrand Mennsesson1, Sara Seager4, Rachel Street5 July 10, 2019 Endorsements Patricia Beauchamp1, John Day1, Russell Genet6, Jason Glenn7, Ryan Mackey1, Marco Quadrelli1, Rebecca Ringuette8, Daniel Stern1, Tiago Vaquero1 1NASA Jet Propulsion Laboratory 2NASA Ames Research Center 3Okean Solutions 4 arXiv:2009.07361v1 [astro-ph.IM] 15 Sep 2020 Massachusetts Institute of Technology 5Las Cumbres Observatory 6California Polytechnic State University 7University of Colorado at Boulder 8University of Iowa a [email protected] c 2019 California Institute of Technology. Government sponsorship acknowledged. 1 Executive Summary Servicing is a legal requirement for WFIRST Autonomy is the ability of a system to achieve and the Flagship mission of the 2030s [5], yet goals while operating independently of exter- past and planned demonstrations may not pro- nal control [1]. The revolutionary advantages vide sufficient future heritage to confidently meet of autonomous systems are recognized in nu- this requirement. In-space assembly (ISA) is cur- merous markets, e.g. automotive, aeronautics. rently being evaluated to construct large aper- Acknowledging the revolutionary impact of au- ture space telescopes [6]. For both servicing and tonomous systems, demand is increasing from ISA, there are questions about how nominal op- consumers and businesses alike and investments erations will be assured, the feasibility of teleop- have grown year-over-year to meet demand. In eration in deep space, and response to anomalies self-driving cars alone, $76B has been invested during robotic operation. from 2014 to 2017 [2]. In the previous Planetary The past decade has seen a revolution in Science Decadal, increased autonomy was identi- the access to space, with low cost launch ve- fied as one of eight core multi-mission technolo- hicles, commercial off-the-shelf technology, and gies required for future missions [3]. -

Intelligence for Space Robotics
INTELLIGENCE FOR SPACE ROBOTICS Edited By Ayanna M. Howard Edward W. Tunstel Georgia Institute of Technology NASA Jet Propulsion Laboratory FOR SPACE CONNOISSEURS AND RESEARCHERS ALIKE Space exploration missions employ robots, instrumented with a variety of sensors and tools, on remote planetary surfaces, on orbit, or as assistants to astronauts. The utility of space robots is a function of their ability to move about, perform work, and explore intelligently without frequent contact with, or strong reliance on, human operators. This requires capabilities for sensing and perception of surrounding unstructured or uncharted environments. It also requires intelligent reasoning about CHAPTERS perceptions to perform tasks in a purposeful and reliable manner in such CHALLENGES OF SPACE ROBOTICS environments. As such, robotic intelligence or autonomy is closely Robotics Challenges for Space and Planetary Robot Systems, related to success of space missions involving robots and automated JPL, USA space systems. With the increasing successes of robotic missions by Space Computing Challenges and Future Directions, JPL, space agencies worldwide, robot autonomy technology has boldly USA confronted the challenging proving grounds of space and its planetary PLANETARY SURFACE ROBOTICS surfaces, further demonstrating its utility and practicality with each Surface Navigation and Mobility Intelligence on the Mars mission. The need for intelligent space robots has increased as well, and Exploration Rovers, JPL, USA will continue to increase with the ever-challenging pursuits of the Vision-Based Localization and Terrain Modeling for international space agencies requiring teams of humans and smart robots. Planetary Rovers, MDA Space Missions, CANADA Design Methodologies for a Colony of Autonomous Space Robot Explorers, Politecnico di Milano, ITALY Space missions present unique robotics challenges. -

Survey of Command Execution Systems for NASA Spacecraft and Robots
V. Verma, A. Jónsson, R. Simmons, T. Estlin, R. Levinson, “Survey of Command Execution Systems for NASA Robots and Spacecraft”, “Plan Execution: A Reality Check” Workshop at The International Conference on Automated Planning & Scheduling (ICAPS), 2005 Survey of Command Execution Systems for NASA Spacecraft and Robots Vandi Verma, Ari Jónsson, Reid Simmons, Tara Estlin, Rich Levinson QSS / NASA Ames Research Center USRA-RIACS / NASA Ames Research Center Carnegie Mellon University Jet Propulsion Lab Attention Control Systems Inc. MS 269-1 NASA Ames, Moffett Field CA 94035 MS 269-2 NASA Ames, Moffett Field CA 94035 3205 Newell-Simon Hall, Carnegie Mellon University, Pittsburgh, PA 15213 M/S 126-347, JPL, Pasadena CA 91109-8099 650 Castro St., Ste 120 PMB 197, Mountain View CA 94041 [email protected], [email protected], [email protected], [email protected], [email protected] Abstract generally only partially known and may even be dynamic. NASA spacecraft and robots operate at long distances from To account for uncertainty even a simple deterministic Earth. Command sequences generated manually, or by sequence of commands needs to use worst-case estimates automated planners on Earth, must eventually be executed of action duration and resource use. In some cases even this autonomously on-board the spacecraft or robot. Software suboptimal sequence may not be robust to the uncertainty. systems that execute commands on-board are known variously as execution systems, virtual machines, or This paper presents a survey of execution systems that have sequence engines. Every robotic system requires some sort been developed for various applications. -

Ad Astra Academy: Using Space Exploration to Promote Student Learning and Motivation in the City of God, Rio De Janeiro, Brazil
Ad Astra Academy: Using Space Exploration to Promote Student Learning and Motivation in the City of God, Rio de Janeiro, Brazil Practice Best Wladimir Lyra Ana Pantelic Paul Hayne New Mexico State University University of Belgrade University of Colorado Boulder [email protected] [email protected] [email protected] Melissa Rice Karolina Garcia Jeffrey Marlow Western Washington University University of Florida Boston University [email protected] [email protected] [email protected] Dhyan Adler-Belendez Leonardo Sattler Cassara Harvard Graduate School of Education (alumnus) Federal University of Rio de Janeiro [email protected] [email protected] Keywords Neil Jacobson Carolyn Crow Astronomy education; Student motivation; Mars University of Southern California University of Colorado Boulder exploration; Astrobiology; Outreach for [email protected] [email protected] Development Motivation is a primary determinant of a student’s academic success, but in many under-resourced educational contexts around the world, opportunities to develop motivation are lacking. In the City of God neighborhood of Rio de Janeiro, Brazil, we, a group of scientists and science educators, enacted the Ad Astra Academy, a brief, interactive intervention targeting teenage students at risk of dropping out of school. Students participated in an immersive five-day programme, followed by a six-month lecture series, before completing the second, immersive three-day programme. Participants learned how to use the scientific method in real-world settings to generate new knowledge. In order to consolidate these knowledge gains and bolster the inspirational power of the programme, capstone projects empowered participants to speak with NASA mission managers and, in some cases, acquire never-before-seen images of Mars. -

Development of Autonomous Actions to Enable the Next Decade of Ocean World Exploration
Ocean Worlds Exploration and Autonomy Decadal Survey 2023-2032 Development of Autonomous Actions to Enable the Next Decade of Ocean World Exploration Corresponding Author: Glenn E. Reeves, Jet Propulsion Laboratory (JPL), California Institute of Technology, [email protected] Co-Authors: Brett A. Kennedy (JPL), Grace H. Tan-Wang (JPL), Paul G. Backes (JPL), Steve A. Chien (JPL), Vandi Verma (JPL), Kevin P. Hand (JPL), Cynthia B. Phillips (JPL) This work was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration (80NM0018D0004). © 2020. California Institute of Technology. Government sponsorship acknowledged Pre-Decisional Information — For Planning and Discussion Purposes Only CL#20-3666 Ocean Worlds Exploration and Autonomy Decadal Survey 2023-2032 1. Executive Summary The development of autonomous actions aboard surface systems is of great value to the exploration of ocean worlds, and the in situ exploration of much of our solar system. The ability of landers to operate with more autonomy than current landers and rovers will enable more and better science, with an overall reduction in cost for comparable missions. In this paper we identify the array of challenges that confront in situ exploration on an ocean world and how many of these challenges are, and have been, addressed (and in some cases resolved) in the early development work for NASA’s Europa Lander mission concept. We identify the pathway for constructing a highly autonomous surface system that enables ocean worlds exploration across an array of targets. Our key developments include: • A system-wide architecture effort to identify the mission activities, and the onboard decisions, that will be required for time- and resource-efficient missions. -

Hyde-A General Purpose Framework For
HyDE – A General Framework for Stochastic and Hybrid Model-based Diagnosis Sriram Narasimhan1 and Lee Brownston2 1University of California, Santa Cruz and 2Perot Systems Government Services, Inc. M/S 269-3, NASA Ames Research Center, Moffett Field, CA-94035 1sriram,[email protected] Abstract diagnosis reasoning (e.g., pure consistency-based, purely In recent years several approaches have been proposed for stochastic and different kinds of search algorithms). model-based diagnosis of hybrid systems. These approaches deal with discrete or parametric faults, and perform In this paper we present the Hybrid Diagnostic Engine consistency-based, stochastic or mixed reasoning. The (HyDE), a general framework for stochastic and hybrid major restriction that a diagnosis application designer faces model-based diagnosis of discrete faults, that is, is that each technique uses its own modeling paradigm and spontaneous changes in operating modes of components. the reasoning algorithms implement a single strategy. HyDE combines ideas from consistency-based [Hamscher, Diagnosis application designers would like to have the et al., 1992; De Kleer and Williams, 1987] and stochastic flexibility of building models that are suitable for the task [Hofbaur and Williams, 2002; Dearden and Clancy, 2002] (e.g., appropriate abstraction level, appropriate details, type of modeling paradigm used). They would also like to have approaches to model-based diagnosis using discrete the flexibility in choosing the strategies used in the [Williams and Nayak, 1996; Kurien and Nayak, 2000], diagnostic reasoning process. continuous [Gertler, 1988; Mosterman and Biswas, 1999] and hybrid [Narasimhan and Biswas, 2003; Hofbaur and We propose a general framework for stochastic and hybrid Williams, 2002; Dearden and Clancy, 2002] models to model-based diagnosis called Hybrid Diagnosis Engine create a flexible and extensible architecture for stochastic (HyDE) that offers this flexibility to the diagnosis and hybrid diagnosis. -
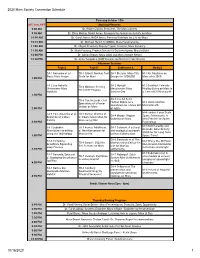
2020 Mars Society Convention Schedule
2020 Mars Society Convention Schedule Thursday October 15th All Times PDT Morning Plenaries 9:00 AM Dr. Robert Zubrin, President, The Mars Society 9:30 AM Dr. Chris McKay, NASA Ames, Prerequisites to Human Activity on Mars 10:00 AM Dr. Carol Stoker, NASA Ames, Potential Habitats for Life on Mars 10:30 AM Dr. Michael Hecht, PI, MOXIE, Mars Perseverance 11:00 AM Dr. Abigail Fraeman, Deputy Project Scientist, Mars Curiosity 11:30 AM Dr. Mark Panning, Project Scientist & Co-Investigator, Mars InSight 12:00 PM Dr. Adrian Brown: Mars 2020 and Mars Sample Return 12:30 PM Dr. Anna Yusupova, IBMP Russia: confinement experiments Afternoon Sessions Tech A Tech B Settlement A Medical TA-1 Romanko et a:l TB-1 Gilbert: Nuclear Fuel SA-1 Bhuiyan: Mars City M-1 Kir: Medicine on Oasis Mars Project Cycle for Mars Design for 1,000,000 Mars after 2050 1:00 PM TA-2 Lee Roberts: SA-2 Haeupli- M-2 Gardiner: Towards TB-2 Nikitaev: Seeding Underwater Mars Meusburger: Mars Healthy Living on Mars in H2 in NTP Engines Habitats Science City a Time of CV19 on Earth 1:30 PM SA-3 Jus Ad Astra: TB-3 Tan, Rezende et al Human Rights as a M-3 Jobin: Martian Operations of a Power foundation for a Mars Bill Mental Health Station on Mars 2:00 PM of rights M-4 Lordos: Large Scale TA-4 Pelc, Suscicka et al; TB-4 Kumar, Sharma et SA-4 Mayes: Utopian Space Settlements: A Evolution of a Mars al: Power Generation for Colonies on Mars New Frontier for Space Colony Mars using CO2 2:30 PM Psychology M-5 Kommareddy and TA-5 Lebedev: TB-5 Kumar, Adlakha et SA-5 Calanchi: A cultural Rezende: -

Autonomous Science Restart for the Planned Europa Mission with Lightweight Planning and Execution
Autonomous Science Restart for the Planned Europa Mission with Lightweight Planning and Execution Vandi Verma, Dan Gaines, Gregg Rabideau, Steve Schaffer, Rajeev Joshi Jet Propulsion Laboratory California Institute of Technology 4800 Oak Grove Drive Pasadena, California 91109 firstname.lastname @jpl.nasa.gov { } Abstract In this paper we present MEXEC - a lightweight on-board Periodic Instrument planning and execution system that monitors spacecraft state calibration Periodic observations Periodic Engineering to robustly respond to current conditions. In addition it Maintenance projects the remaining plan forward in time to detect con- flicts and revise the plan. Most current planetary missions use sequence based com- manding from the ground, which limits the ability to respond Instrument to on-board state varying from planned for state. This re- calibration Periodic/continuous observations Manuvers GNC Attain Periodic Targeting sults in planning for worst-case execution time, power uti- UVS Scan Init Europa Closest Approach lization, data volume and other resources and leads to under- Flyby Periodic utilization of the spacecraft capability. It also limits the abil- Instrument DSN Tracks calibration GNC Attain ity to respond to faults. Earth Due to the high radiation environment at Jupiter the prob- ability of flight software resets is high. Therefore, of partic- ular interest to the planned Europa Mission is the capability to restart the science plan after flight software resets. In this Figure 1: Simplified Jovian Orbit and Flyby Segment. paper we present results from running Europa flyby scenar- ios with flight software resets in the Europa flight software test environment. Preliminary results with the prototype sce- nario show MEXEC takes less than a tenth of a second to Sequencing Approach and Related Work respond to resets. -

Ssim: NASA Mars Rover Robotics Flight Software Simulation
SSim: NASA Mars Rover Robotics Flight Software Simulation Vandi Verma, Chris Leger Mobility and Robotics Systems Section NASA Jet Propulsion Laboratory California Institute of Technology 4800 Oak Grove Drive, Pasadena California, USA [email protected], [email protected] Abstract—Each new Mars rover has pursued increasingly richer 10. CONCLUSIONS .....................................9 science while tolerating a wider variety of environmental condi- ACKNOWLEDGMENTS ................................ 10 tions and hardware degradation over longer mission operation duration. Sojourner operated for 83 sols (Martian days), Spirit REFERENCES ......................................... 10 for 2208 sols, and Opportunity is at 5111 sols, and Curiosity BIOGRAPHY .......................................... 11 operation is ongoing at 2208 sols. To handle this increase in ca- pability, the complexity of onboard flight software has increased. MSL (also known as Curiosity), uses more flight software lines of code than all previous missions to Mars combined, including 1. INTRODUCTION both successes and failures[1]. MSL has more than 4,200 com- mands with as many as dozens of arguments, 54,000 parameters, Mars science is an active area of research, and there are and tens of thousands of additional state variables. A single 500 planetary scientists that participate in MSL operations. high-level command may perform hours of configurable robotic Analysis and discussion of observations made by the rover arm and sampling behavior. Incorrect usage can result in the typically impact the goals for subsequent observations. Un- loss of an activity or the loss of the mission. Surface Simulation like most deep space and Earth orbiting missions for which (“SSim”) was developed to address the challenge of making full operations are typically planned weeks, months and even and effective use of many capabilities of MSL, while managing years in advance, Mars rover operations are planned daily complexity and risk. -

So You Passed an Earned Value Management Government Validation - Now What?
2019 IEEE Aerospace Conference (AERO 2019) Big Sky, Montana, USA 2-9 March 2019 Pages 1-820 IEEE Catalog Number: CFP19AAC-POD ISBN: 978-1-5386-6855-9 1/6 Copyright © 2019 by the Institute of Electrical and Electronics Engineers, Inc. All Rights Reserved Copyright and Reprint Permissions: Abstracting is permitted with credit to the source. Libraries are permitted to photocopy beyond the limit of U.S. copyright law for private use of patrons those articles in this volume that carry a code at the bottom of the first page, provided the per-copy fee indicated in the code is paid through Copyright Clearance Center, 222 Rosewood Drive, Danvers, MA 01923. For other copying, reprint or republication permission, write to IEEE Copyrights Manager, IEEE Service Center, 445 Hoes Lane, Piscataway, NJ 08854. All rights reserved. *** This is a print representation of what appears in the IEEE Digital Library. Some format issues inherent in the e-media version may also appear in this print version. IEEE Catalog Number: CFP19AAC-POD ISBN (Print-On-Demand): 978-1-5386-6855-9 ISBN (Online): 978-1-5386-6854-2 ISSN: 1095-323X Additional Copies of This Publication Are Available From: Curran Associates, Inc 57 Morehouse Lane Red Hook, NY 12571 USA Phone: (845) 758-0400 Fax: (845) 758-2633 E-mail: [email protected] Web: www.proceedings.com TABLE OF CONTENTS SO YOU PASSED AN EARNED VALUE MANAGEMENT GOVERNMENT VALIDATION - NOW WHAT? ..................................................................................................................................................................................1 William Liggett ; Howard Hunter ; Matthew Jones AUTOMATED SPACECRAFT OPERATIONS DURING SOIL MOISTURE ACTIVE PASSIVE PRIME MISSION................................................................................................................................................................ 11 Masashi Mizukami ; Christopher G.