Preliminary Work on the Prediction of Extreme Rainfall Events and Flood Events in Australia
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

February 2021
Monthly Weather Review Australia February 2021 The Monthly Weather Review - Australia is produced by the Bureau of Meteorology to provide a concise but informative overview of the temperatures, rainfall and significant weather events in Australia for the month. To keep the Monthly Weather Review as timely as possible, much of the information is based on electronic reports. Although every effort is made to ensure the accuracy of these reports, the results can be considered only preliminary until complete quality control procedures have been carried out. Any major discrepancies will be noted in later issues. We are keen to ensure that the Monthly Weather Review is appropriate to its readers' needs. If you have any comments or suggestions, please contact us: Bureau of Meteorology GPO Box 1289 Melbourne VIC 3001 Australia [email protected] www.bom.gov.au Units of measurement Except where noted, temperature is given in degrees Celsius (°C), rainfall in millimetres (mm), and wind speed in kilometres per hour (km/h). Observation times and periods Each station in Australia makes its main observation for the day at 9 am local time. At this time, the precipitation over the past 24 hours is determined, and maximum and minimum thermometers are also read and reset. In this publication, the following conventions are used for assigning dates to the observations made: Maximum temperatures are for the 24 hours from 9 am on the date mentioned. They normally occur in the afternoon of that day. Minimum temperatures are for the 24 hours to 9 am on the date mentioned. They normally occur in the early morning of that day. -

SOLONEC Shared Lives on Nigena Country
Shared lives on Nigena country: A joint Biography of Katie and Frank Rodriguez, 1944-1994. Jacinta Solonec 20131828 M.A. Edith Cowan University, 2003., B.A. Edith Cowan University, 1994 This thesis is presented for the degree of Doctor of Philosophy of The University of Western Australia School of Humanities (Discipline – History) 2015 Abstract On the 8th of December 1946 Katie Fraser and Frank Rodriguez married in the Holy Rosary Catholic Church in Derby, Western Australia. They spent the next forty-eight years together, living in the West Kimberley and making a home for themselves on Nigena country. These are Katie’s ancestral homelands, far from Frank’s birthplace in Galicia, Spain. This thesis offers an investigation into the social history of a West Kimberley couple and their family, a couple the likes of whom are rarely represented in the history books, who arguably typify the historic multiculturalism of the Kimberley community. Katie and Frank were seemingly ordinary people, who like many others at the time were socially and politically marginalised due to Katie being Aboriginal and Frank being a migrant from a non-English speaking background. Moreover in many respects their shared life experiences encapsulate the history of the Kimberley, and the experiences of many of its people who have been marginalised from history. Their lives were shaped by their shared faith and Katie’s family connections to the Catholic mission at Beagle Bay, the different governmental policies which sought to assimilate them into an Australian way of life, as well as their experiences working in the pastoral industry. -

Annual Report 2011–12 Navigation and Printing This Annual Report Has Been Created for Optimal Viewing As an Electronic, Online Document
DEPARTMENT OF NATURAL RESOURCES, ENVIRONMENT, THE ARTS AND SPORT Annual Report 2011–12 Navigation and Printing This Annual Report has been created for optimal viewing as an electronic, online document. This electronic format has been followed in accordance with the Northern Territory Government’s Annual Report Policy. It is best viewed online at ‘Fit Page’ settings, by pressing the Ctrl and 0 (Zero) keys on your keyboard. For optimal print settings set page scaling at ‘Fit to Printer Margins’, by going to File, Print and altering your options under page handling to ‘Fit to Printer Margins’. To search the entire Annual Report and supporting documents, press the Ctrl and F keys on your keyboard, and type in your search term. The Northern Territory Department of Natural Resources, Environment, The Arts and Sport would like to advise readers that this document might contain pictures of Aboriginal and Torres Strait Island people that may offend. © Northern Territory Government Northern Territory Department of Natural Resources, Environment, The Arts and Sport PO 496 Palmerston NT 0831 www.nt.gov.au/nretas Published October 2012 by the Northern Territory Department of Natural Resources, Environment, The Arts and Sport ISSN 1834-0571 Introduction Purpose of the Report Target Audience This Annual Report provides a record of the Department of Natural This Annual Report provides information to numerous target audiences on Resources, Environment and The Arts and Sport and the Territory Wildlife the Agency’s activities and achievements for the 2011–12 financial year. Parks Government Business Division’s achievements for the 2011–12 It is tabled in the Northern Territory Legislative Assembly primarily as an financial year. -

Queensland in January 2011
HOME ABOUT MEDIA CONTACTS Search NSW VIC QLD WA SA TAS ACT NT AUSTRALIA GLOBAL ANTARCTICA Bureau home Climate The Recent Climate Regular statements Tuesday, 1 February 2011 - Monthly Climate Summary for Queensland - Product code IDCKGC14R0 Queensland in January 2011: Widespread flooding continued Special Climate Statement 24 (SCS 24) titled 'Frequent heavy rain events in late 2010/early 2011 lead to Other climate summaries widespread flooding across eastern Australia' was first issued on 7th Jan 2011 and updated on 25th Jan 2011. Latest season in Queensland High rainfall totals in the southeast and parts of the far west, Cape York Peninsula and the Upper Climate Carpentaria Latest year in Queensland Widespread flooding continued Outlooks Climate Summary archive There was a major rain event from the 10th to the 12th of January in southeast Queensland Reports & summaries TC Anthony crossed the coast near Bowen on the 30th of January Earlier months in Drought The Brisbane Tropical Cyclone Warning Centre (TCWC) took over responsibility for TC Yasi on the Queensland Monthly weather review 31st of January Earlier seasons in Weather & climate data There were 12 high daily rainfall and 13 high January total rainfall records Queensland Queensland's area-averaged mean maximum temperature for January was 0.34 oC lower than Long-term temperature record Earlier years in Queensland average Data services All Climate Summary Maps – recent conditions Extremes Records Summaries Important notes the top archives Maps – average conditions Related information Climate change Summary January total rainfall was very much above average (decile 10) over parts of the Far Southwest district, the far Extremes of climate Monthly Weather Review west, Cape York Peninsula, the Upper Carpentaria, the Darling Downs and most of the Moreton South Coast About Australian climate district, with some places receiving their highest rainfall on record. -

Monthly Weather Review Australia January 2021
Monthly Weather Review Australia January 2021 The Monthly Weather Review - Australia is produced by the Bureau of Meteorology to provide a concise but informative overview of the temperatures, rainfall and significant weather events in Australia for the month. To keep the Monthly Weather Review as timely as possible, much of the information is based on electronic reports. Although every effort is made to ensure the accuracy of these reports, the results can be considered only preliminary until complete quality control procedures have been carried out. Any major discrepancies will be noted in later issues. We are keen to ensure that the Monthly Weather Review is appropriate to its readers' needs. If you have any comments or suggestions, please contact us: Bureau of Meteorology GPO Box 1289 Melbourne VIC 3001 Australia [email protected] www.bom.gov.au Units of measurement Except where noted, temperature is given in degrees Celsius (°C), rainfall in millimetres (mm), and wind speed in kilometres per hour (km/h). Observation times and periods Each station in Australia makes its main observation for the day at 9 am local time. At this time, the precipitation over the past 24 hours is determined, and maximum and minimum thermometers are also read and reset. In this publication, the following conventions are used for assigning dates to the observations made: Maximum temperatures are for the 24 hours from 9 am on the date mentioned. They normally occur in the afternoon of that day. Minimum temperatures are for the 24 hours to 9 am on the date mentioned. They normally occur in the early morning of that day. -

The Nature of Northern Australia
THE NATURE OF NORTHERN AUSTRALIA Natural values, ecological processes and future prospects 1 (Inside cover) Lotus Flowers, Blue Lagoon, Lakefield National Park, Cape York Peninsula. Photo by Kerry Trapnell 2 Northern Quoll. Photo by Lochman Transparencies 3 Sammy Walker, elder of Tirralintji, Kimberley. Photo by Sarah Legge 2 3 4 Recreational fisherman with 4 barramundi, Gulf Country. Photo by Larissa Cordner 5 Tourists in Zebidee Springs, Kimberley. Photo by Barry Traill 5 6 Dr Tommy George, Laura, 6 7 Cape York Peninsula. Photo by Kerry Trapnell 7 Cattle mustering, Mornington Station, Kimberley. Photo by Alex Dudley ii THE NATURE OF NORTHERN AUSTRALIA Natural values, ecological processes and future prospects AUTHORS John Woinarski, Brendan Mackey, Henry Nix & Barry Traill PROJECT COORDINATED BY Larelle McMillan & Barry Traill iii Published by ANU E Press Design by Oblong + Sons Pty Ltd The Australian National University 07 3254 2586 Canberra ACT 0200, Australia www.oblong.net.au Email: [email protected] Web: http://epress.anu.edu.au Printed by Printpoint using an environmentally Online version available at: http://epress. friendly waterless printing process, anu.edu.au/nature_na_citation.html eliminating greenhouse gas emissions and saving precious water supplies. National Library of Australia Cataloguing-in-Publication entry This book has been printed on ecoStar 300gsm and 9Lives 80 Silk 115gsm The nature of Northern Australia: paper using soy-based inks. it’s natural values, ecological processes and future prospects. EcoStar is an environmentally responsible 100% recycled paper made from 100% ISBN 9781921313301 (pbk.) post-consumer waste that is FSC (Forest ISBN 9781921313318 (online) Stewardship Council) CoC (Chain of Custody) certified and bleached chlorine free (PCF). -

C Om M U N It Y in F Or M a T
COMMUNITY INFORMATION The horse drawn tramway extended extended to a length of 120 metres. The ART & HISTORY from the Jetty down Loch Street as far flow from the bore was dropping off even The Spirit of the Wandjina Art Studio as the King Sound Hotel site. Nearby by 1919. Now water is pumped into the at Mowanjum Aboriginal Community was a quarry that was used to supply trough by a windmill. The water from the welcomes visitors. Phone (08) 9191 stone for the causeway across the bore has a rich mineral content and was 1008. Work from this community was a mud flats. The tramway finished near reputed to have therapeutic properties. A feature of the opening ceremony of the McGovern and Thompson’s Store (now bath house once stood near the trough. Sydney Olympics. Norval’s Gallery located Woolworths). (see the Boab Prison Tree Interpretative on Loch Street, opposite Lytton Park, Pavilion located on site for further Those wishing to follow up on the story has a large range of local artwork from information). of the SS Colac can view the anchor throughout the region. Jila Gallery & Café and propeller of the vessel in the Lions located in Clarendon Street showcases Park in front of the Derby Civic Centre in BOAB PRISON TREE the art of the Looma Community 120kms Loch Street. The remains of the vessel 7km from Derby on the Derby – south east of Derby, plus local Derby can be viewed at low tide out from the Broome Highway artists. end of the Derby airport runway via a This huge tree is believed to be around fixed wing or helicopter flight. -
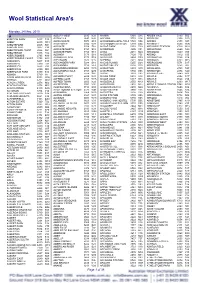
Wool Statistical Area's
Wool Statistical Area's Monday, 24 May, 2010 A ALBURY WEST 2640 N28 ANAMA 5464 S15 ARDEN VALE 5433 S05 ABBETON PARK 5417 S15 ALDAVILLA 2440 N42 ANCONA 3715 V14 ARDGLEN 2338 N20 ABBEY 6280 W18 ALDERSGATE 5070 S18 ANDAMOOKA OPALFIELDS5722 S04 ARDING 2358 N03 ABBOTSFORD 2046 N21 ALDERSYDE 6306 W11 ANDAMOOKA STATION 5720 S04 ARDINGLY 6630 W06 ABBOTSFORD 3067 V30 ALDGATE 5154 S18 ANDAS PARK 5353 S19 ARDJORIE STATION 6728 W01 ABBOTSFORD POINT 2046 N21 ALDGATE NORTH 5154 S18 ANDERSON 3995 V31 ARDLETHAN 2665 N29 ABBOTSHAM 7315 T02 ALDGATE PARK 5154 S18 ANDO 2631 N24 ARDMONA 3629 V09 ABERCROMBIE 2795 N19 ALDINGA 5173 S18 ANDOVER 7120 T05 ARDNO 3312 V20 ABERCROMBIE CAVES 2795 N19 ALDINGA BEACH 5173 S18 ANDREWS 5454 S09 ARDONACHIE 3286 V24 ABERDEEN 5417 S15 ALECTOWN 2870 N15 ANEMBO 2621 N24 ARDROSS 6153 W15 ABERDEEN 7310 T02 ALEXANDER PARK 5039 S18 ANGAS PLAINS 5255 S20 ARDROSSAN 5571 S17 ABERFELDY 3825 V33 ALEXANDRA 3714 V14 ANGAS VALLEY 5238 S25 AREEGRA 3480 V02 ABERFOYLE 2350 N03 ALEXANDRA BRIDGE 6288 W18 ANGASTON 5353 S19 ARGALONG 2720 N27 ABERFOYLE PARK 5159 S18 ALEXANDRA HILLS 4161 Q30 ANGEPENA 5732 S05 ARGENTON 2284 N20 ABINGA 5710 18 ALFORD 5554 S16 ANGIP 3393 V02 ARGENTS HILL 2449 N01 ABROLHOS ISLANDS 6532 W06 ALFORDS POINT 2234 N21 ANGLE PARK 5010 S18 ARGYLE 2852 N17 ABYDOS 6721 W02 ALFRED COVE 6154 W15 ANGLE VALE 5117 S18 ARGYLE 3523 V15 ACACIA CREEK 2476 N02 ALFRED TOWN 2650 N29 ANGLEDALE 2550 N43 ARGYLE 6239 W17 ACACIA PLATEAU 2476 N02 ALFREDTON 3350 V26 ANGLEDOOL 2832 N12 ARGYLE DOWNS STATION6743 W01 ACACIA RIDGE 4110 Q30 ALGEBUCKINA -

Special Climate Statement 43
SPECIAL CLIMATE STATEMENT 43 Extreme January heat Last update 7 January, 2013 Climate Information Services Bureau of Meteorology Note: This statement is based on data available as of 7 January 2013 which may be subject to change as a result of standard quality control procedures. Introduction Large parts of central and southern Australia are currently under the influence of a persistent and widespread heatwave event. This event is ongoing with further significant records likely to be set. Further updates of this statement and associated significant observations will be made as they occur, and a full and comprehensive report on this significant climatic event will be made when the current event ends. The last four months of 2012 were abnormally hot across Australia, and particularly so for maximum (day-time) temperatures. For September to December (i.e. the last four months of 2012) the average Australian maximum temperature was the highest on record with a national anomaly of +1.61 °C, slightly ahead of the previous record of 1.60 °C set in 2002 (national records go back to 1910). In this context the current heatwave event extends a four month spell of record hot conditions affecting Australia. These hot conditions have been exacerbated by very dry conditions affecting much of Australia since mid 2012 and a delayed start to a weak Australian monsoon. The start of the current heatwave event traces back to late December 2012, and all states and territories have seen unusually hot temperatures with many site records approached or exceeded across southern and central Australia. A full list of records broken at stations with long records (>30 years) is given below. -

A Timeline of Western Australia's Fitzroy River Catchment (Report)
Looking back to look forward: A timeline of Western Australia’s Fitzroy River catchment Report Jorge G. Álvarez-Romero, Milena Kiatkoski Kim, Rachel Buissereth, Robert L. Pressey, David Pannell, Michael M. Douglas, Alaya Spencer-Cotton © James Cook University, 2021 Looking back to look forward: A timeline of Western Australia’s Fitzroy River is licensed by James Cook University for use under a Creative Commons Attribution Non-commercial licence. For licence conditions see creativecommons.org/licenses/by-nc/4.0 This report should be cited as: Álvarez-Romero, J.G.,1 M. Kiatkoski Kim,2 R. Buissereth,3 R.L. Pressey,1 D. Pannell,2 M.M. Douglas,4 & A. Spencer-Cotton.2 2021. Looking back to look forward: A timeline of Western Australia’s Fitzroy River catchment. Report to the Australian Department of Agriculture, Water and the Environment. James Cook University, Townsville. DOI: 10.25903/hq6b-kk36 1. Australian Research Council Centre of Excellence for Coral Reef Studies, James Cook University, Townsville, QLD 4810, Australia 2. Centre for Environmental Economics and Policy, School of Agriculture and Environment, The University of Western Australia, Crawley, WA 6009, Australia 3. CSIRO and James Cook University Division of Tropical Environments and Societies, Cairns, QLD 4878, Australia 4. School of Biological Sciences, The University of Western Australia, Crawley, WA 6009, Australia View at publisher website: https://researchonline.jcu.edu.au/68184 The Story Map application can be accessed at https://arcg.is/1jXi9P – use Google Chrome browser for better results. The online application should be cited as: Álvarez-Romero, J.G. & R. Buissereth. 2021. Looking back to look forward: A timeline of the Fitzroy River catchment, Story Map. -

Eco Feb 06.Indd
f o r u m NEW AIR CONDITIONING DESIGN TEMPERATURES FOR QUEENSLAND, AUSTRALIA Eric Peterson¹, Nev Williams¹, Dale Gilbert¹, Klaus Bremhorst² ABSTRACT This paper presents results of a detailed analysis of meteorological data to determine air conditioning design temperatures dry bulb and wet bulb for hundreds of locations throughout Queensland, using the tenth-highest daily maximum observed per year. This is a modification of the AIRAH 1997 method that uses only 3:00pm records of temperature. In this paper we ask the reader to consider Australian Bureau of Meteorology official “climate summaries” as a benchmark upon which to compare various previously published comfort design temperatures, as well as the new design temperatures proposed in the present paper. We see some possible signals from climate change, but firstly we should apply all available historical data to establish outdoor design temperatures that will ensure that cooling plant are correctly sized in the near future. In a case-studies of Brisbane, we find that inner city temperatures are rising, that airport temperatures are not, and that suburban variability is substantially important. Keywords: air conditioning design, Queensland, climate data Background is in their personal control (Khedari and Yamtraipat 2000 Results of the present paper are abridged in Table 1, in and Nicol, et al. 1999). Floating indoor temperatures during comparison with design temperatures for eight key sites hot weather is not a new operational policy in Queensland, previously published by AIRAH, and five -

New Air Conditioning Design Temperatures for Queensland
New air-conditioning design temperatures for Queensland, Australia by Eric Peterson¹, Nev Williams¹, Dale Gilbert¹, Klaus Bremhorst² ¹Thermal Comfort Initiative of Queensland Department of Public Works, Brisbane ²Professor of Mechanical Engineering, the University of Queensland, St Lucia Abstract : This paper presents results of a detailed analysis of meteorological data to determine air conditioning design temperatures dry bulb and wet bulb for hundreds of locations throughout Queensland, using the tenth-highest daily maximum observed per year. This is a modification of the AIRAH 1997 method that uses only 3PM records of temperature. In this paper we ask the reader to consider Australian Bureau of Meteorology official “climate summaries” as a benchmark upon which to compare various previously published comfort design temperatures, as well as the new design temperatures proposed in the present paper. We see some possible signals from climate change, but firstly we should apply all available historical data to establish outdoor design temperatures that will ensure that cooling plant are correctly sized in the near future. In a case- studies of Brisbane, we find that inner city temperatures are rising, that airport temperatures are not, and that suburban variability is substantially important. Table 1: Air-conditioning design temperatures compared at eight locations 2004 1986 2004 2004 1975 2004 1998 AERO AERO BRISBANE 1939 – 1942 – 1851 – 1939 – 1942 – 1957 – 1950 – 2000 1940 – TOOWOOMBA CAIRNSAERO CHARLEVILLE (EAGLE FARM) ROCKHAMPTON BRISBANE